基于调整轮廓线权重的文物碎块自动拼接方法
2021-06-28耿国华姚文敏周明全徐雪丽刘阳洋
耿国华,姚文敏,周明全,刘 杰,徐雪丽,4, 曹 欣,刘阳洋,李 康
(1.西北大学 信息科学与技术学院,陕西 西安 710127;2.西北大学 文化遗产数字化国家地方联合工程研究中心, 陕西 西安 710127;3.北京师范大学 教育部虚拟现实应用工程研究中心,北京 100875;4.延安大学 数学与计算机科学学院,陕西 延安 716000)
地壳运动、气候变化、收藏和搬运等过程中的不当操作都可能使文物破损,进而影响其艺术、历史等价值,因此,拼接碎片以恢复文物原貌是一项重要工作。传统的手工拼接不仅繁琐,而且可能在拼接过程中对文物造成二次破坏[1]。计算机技术的发展使虚拟拼接技术取代手工操作成为可能。在大量待处理碎块中,虚拟拼接技术能够自动选择合适的碎块进行拼接,最终实现整体复原。该过程包括两个阶段:匹配与配准,前者确定哪些碎块应该拼接在一起,后者确定如何拼接。
三维物体匹配的通用方法是:提取物体的特征之后对特征描述子进行比对,确定物体之间的匹配关系。根据不同的特征来源,可以将这些方法归为基于点[2-3]、基于线[4-7]和基于面[8-9]3类。PAN等通过检测物体的关键点,对其局部特征进行编码,利用能量函数对局部特征和欧几里得几何混合空间中临界点的相似性进行建模,完成相应匹配任务[2]。袁洁等通过构建轮廓线到断裂面和表面特征点的双向距离描述子[7],提高了特征的鲁棒性,但该方法对轮廓线有较高的依赖性,在轮廓线严重缺损时表现不佳。Son等提出了一种基于表面的描述符(surface signature),用于描述基于凹凸信息的几何特征,以衡量不同表面的相似性[9]。总体而言,从点到线再到面的特征描述子包含的信息逐渐丰富,对噪声的抗干扰程度逐渐增强。
配准的解决方案主要可分为3种[10]:基于距离[11-15]、基于滤波器[16-18]和基于概率分布[19-22]。迭代最近点(iterative closest point, ICP)算法[11]是基于距离的三维点云配准方法。ICP以三维点云之间的欧式距离为优化目标,迭代更新点云与空间位姿的对应关系。为了解决更具体、更复杂的问题,研究者们提出了一系列基于ICP的改进方法[12-15],但此类方法仍存在计算量大、收敛时间长、局部最优以及对噪声敏感等缺点[23]。Sandhu等采用粒子滤波方案驱动点集的配准过程,对噪声与结构缺失等问题具有较好鲁棒性[18]。Jian等将三维点云表示为高斯混合模型,并将点云配准问题视为对两个高斯混合模型的配准[19]。此外,三维点云配准通常使用由粗到精的配准策略[24]。Kim等联合主成分分析(principal component analysis, PCA)和ICP算法使用基于PCA的全局配准粗略对齐三维数据,得到位置的初始估计,然后,采用ICP和Levenberg-Marquardt算法进行局部对齐得到更精细的配准结果,提高了算法的效率和精度[25]。此外,Wang等[26]提出了深度最近点(deep closest point, DCP)神经网络,由于其训练样本为理想状态下的三维物体,因此,若直接将该方法应用于现实问题,效果并不突出。
为了提高对破损轮廓线的鲁棒性,本文提出一种基于断裂面信息的文物碎块自动拼接方法,该方法能够降低对轮廓线的依赖程度,同时有效解决PCA配准的方向歧义性,并且通过构建的由粗到细的配准方法,得到更精准的拼接结果。
1 方法描述
1.1 断裂面提取
与文物外表面不同,断裂面是因断裂而产生的新表面,如图1所示。断裂面包含重要的纹理和几何分布信息,能够为匹配阶段提供丰富的特征和有力的支持。本文参考Li等[27]的断裂面提取方法,根据多尺度曲率确定断裂面轮廓线,比较平面粗糙程度来区分断裂面和外表面,断裂面提取结果如图2所示。

图1 不同视角下的兵马俑碎块Fig.1 Terracotta Warriors fragment from different perspectives

图2 断裂面提取结果Fig.2 Extraction result of fracture surface
1.2 特征提取与匹配
快速点特征直方图(fast point feature histograms,FPFH)[28]在三维点云关键点检测、匹配和配准等领域有广泛的应用。文物最初断裂产生的轮廓线比较尖锐,但轮廓线位于断裂面外沿,经历长期自然以及人为因素的影响极易磨损。因此,高度依赖轮廓线的方法可能因特征的不可靠性导致性能下降。基于此,本文提出基于改进的FPFH特征的文物断裂面特征提取与匹配算法,降低对轮廓线的依赖度。算法描述如图3所示,以一对待处理的断裂面作为输入,经过FPFH特征提取和比对得到匹配点,再根据该点是否位于轮廓线上,调整其对断裂面的整体匹配度的权重,最终输出匹配得分。

图3 文物断裂面特征提取与匹配算法示意图Fig.3 Schematic diagram of the feature extraction and matching algorithm of cultural relics fracture surfaces
以断裂面A,B为例,其分别由m和n个点组成,即A={a1,a2,…,am},B={b1,b2,…,bn}。 计算各点的FPPH特征, 得到FA={fa1,fa2,…,fam},FB={fb1,fb2,…,fbn}。A中任意一点对应的匹配点为B中在FPPH特征向量空间中欧式距离接近的点。例如,若‖fai,fbj‖≤ξ,则ai与bj为一对匹配点,ξ为判断点是否匹配的阈值。根据匹配点数占断裂面上总点数的比例,确定最终的断裂面匹配得分,
(1)
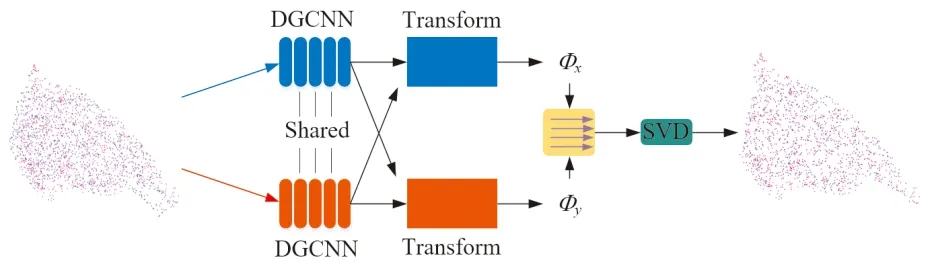
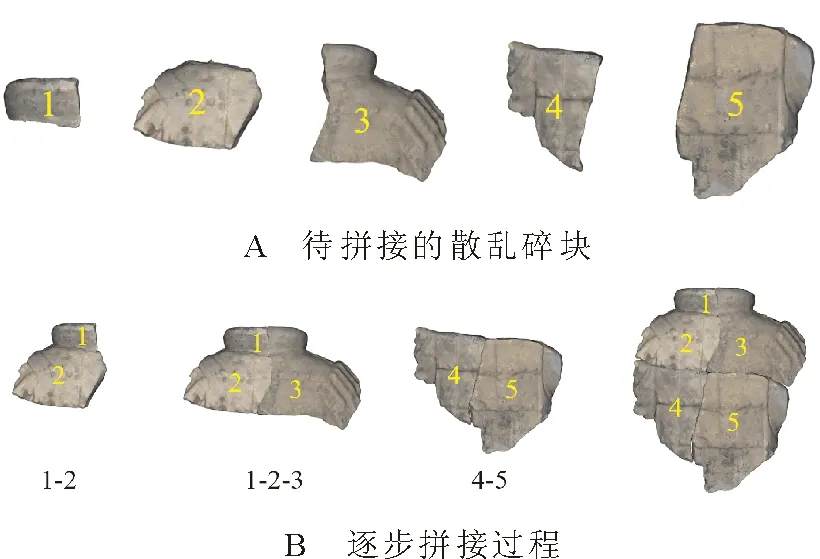
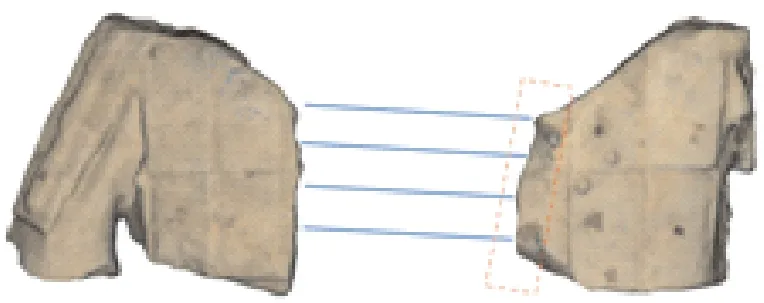
其中,若第i个点为匹配点,则Mi=1,否则Mi=0;若第i个点为轮廓线上的点,则wi=wc,否则wi=wp。wc表示轮廓线上点的权重,wp表示非轮廓线上点的权重,且wc 确定匹配关系后,下一步进行配准。给定三维物体P和Q,配准任务可以表述为:求解旋转矩阵R和平移向量T以达到优化目标,优化目标是PR+T尽量与Q重合。 由于断裂面是所属碎块的子集,二者共享同一个坐标系,因此,将根据断裂面获得的参数R与T用于碎块即可实现碎块拼接。匹配的断裂面之间,形状分布也较为接近。对于一个匹配碎块对,本文利用PCA分别获得其3个主方向,将其作为配准对象,取代了对断裂面全体点进行配准,加快粗配准的速度,粗配准过程如图4所示。 图4 断裂面粗配准过程Fig.4 Fracture surfaces coarse registration process H=USV,R=VUT, (2) 其中:U和V均为单位正交阵,分别称为左右奇异矩阵;S的主对角线上为奇异值,其他元素为0;R即为所求的旋转矩阵。平移向量T=CB-CA,CA与CB分别是断裂面A与B的质心。质心可通过计算断裂面的三维坐标平均值获得,以A为例,有 (3) 然而,基于PCA的粗配准方法会带来配准方向产生歧义的问题。A的任何一个主方向都可与B的两种配准主方向相对应,即:xA与xB,或xA与-xB。所以3个主方向会产生8种配准方向,在主方向间相对位置的约束下,最后可能的配准方向有4种,分别是: 这4种可能的配准方向的配准结果如图5所示。 图5 4种配准方向Fig.5 Four registration directions 鉴于方向歧义的问题,本文分别实现了上述4种方向的配准,并评价其配准效果,最终择优选取。在此,以两个断裂面之间的距离为评价标准,即 D=DAB+DBA, (4) (5) (6) (7) (8) 其中,DAB表示A到B的距离,即A中每个点到B中点最短距离的平均值,DBA同理。D作为两个面之间距离的均值,可以体现点云的重合程度,用以评价配准质量。如图5A对应的D最小,因此被确定为最终选择。 深度最近点(deep closest point,DCP)模型是一种解决三维配准问题的深度学习方法。通过编码模块、注意力模块以及奇异值分解模块,DCP可以自动求解待配准物体间的旋转矩阵R和平移向量T。DCP的编码模块采用动态图卷积(dynamic graph convolution neural network, DGCNN),提取点云的深度特征,注意力模块用于调整待配准物体的关联特征,SVD模块用于计算R和T,DCP模型结构如图6所示。在实验过程中,DCP的训练集与测试集均为理想状态,即配准对象之间形状完全重合,仅在位置上有区别。然而实际情况与理想状态有很大差别:在数据采集的过程中,不同文物碎块作为单独的个体被分开处理,故在数据密度、精度以及形状结构上均有差别,所以直接将DCP应用于文物配准,效果并不理想。 图6 DCP架构Fig.6 Structure of DCP 本文针对文物的特殊性,构造完全由文物数据组成的数据集,对DCP进行迁移训练,得到适用于文物配准的DCP网络,并且与PCA结合,通过PCA给定初始的位姿估计,再使用DCP进行细微调整,最终实现配准精度的提升。 实验数据均为兵马俑碎块,由秦始皇兵马俑博物馆提供,西北大学文化遗产数字化国家地方联合工程研究中心整理入库,通过Artec Eva手持扫描仪获取。实验分为两个部分:一是仿真实验,二是真实场景实验。 仿真实验所用数据包括两部分:标准数据集ModelNet40和兵马俑碎块数据。DCP网络先在标准数据集上进行预训练,然后迁移至兵马俑碎块上继续训练。关于兵马俑数据,本文通过随机旋转,平移,裁剪等处理,得到包含1 800对待配准碎块断裂面的数据集,仿真了现实场景。此数据集以4∶1的比例分为训练集和测试集。在测试集上,除了本文方法之外,选取了ICP[11]、DCP[26]、单独使用PCA,以及PCA与ICP联合共4种方法作为对比,对比结果如表1所示。评价指标主要有3个: 1)配准成功率。统计配准成功的样本占所有实验样本的比例,配准结果中碎块断裂面之间的角度以及距离在一定范围内即视为配准成功(角度误差在10°之内,距离误差在20 mm之内)。 2)距离误差。统计所有成功样本断裂面之间距离的均方误差MSE和平均绝对误差MAE,断裂面之间距离的定义见公式(4)。 3)计算开销。统计所有样本所需的平均迭代计算次数。 表1 不同配准方法在兵马俑碎块上实验结果对比Tab.1 The experimental results comparison of different registration methods implemented on the Terracotta Warriors fragments 从表1的实验结果可以看出,由于ICP算法迭代运算的特点,其在成功率、误差和计算开销上表现最差; DCP方法的成功率很低,但是在配准成功的实例上误差较小;PCA作为粗配准方法,配准成功率很高,但是在细尺度的精度上不够理想,反映为较高的距离误差。 本文提出的PCA+DCP方法在各个指标上均表现最佳,且未引入迭代运算,计算开销得以保证。与单独使用PCA或者DCP相比,本文方法结合PCA的快速粗配准以及DCP在细配准阶段的优势,弥补了前者精度不足以及后者成功率不高的缺陷。图7为一对待配准断裂面的不同拼接结果对比图。由图7可知,PCA获得了总体的配准结果,但在细节上表现不佳;DCP在失去PCA的支持后,在该样本上配准失败;而结合了PCA和DCP的方法取得了最佳的配准结果。 图7 具体样本配准结果对比Fig.7 Comparison of registration results of a specific sample PCA方法作为优秀的粗配准方法,能为后续细配准提供良好的初始化结果,不仅可以与DCP结合,也可以与ICP结合。由表1可以看出,PCA可以全面提升ICP的性能,但属于单方面提升,依旧落后于PCA本身。本文提出的PCA+DCP的方案可以实现二者的优势互补,实现最佳配准效果。 真实场景中,两个被拼接在一起的碎块可以作为一个新的碎块加入到下一轮拼接过程中。以“G10-36”号兵马俑背部为例,本文方法的拼接过程如图8所示。 图8 “G10-36”号兵马俑背部拼接结果Fig.8 Reassembly process of back of Terracotta Warriors labeled “G10-36” 在拼接过程中,本文统计了匹配得分。此得分作为判断碎块是否匹配的依据,越靠近真实值则说明匹配结果越合理,即:对于匹配碎块,匹配得分应尽量趋于1,对于不匹配碎块,匹配得分应尽量趋于0。本例中,每一步匹配的匹配得分如表2,其中,判断匹配点的阈值ξ=20,轮廓线上点的权重wc=0.8,非轮廓线上点的权重wp=1.0。为了验证权重调整的必要性,以未经过轮廓线权重调整的FPFH方法作为对比。在匹配得分方面,本方法由于降低了轮廓线权重,更加信赖非轮廓线,因此得到的匹配得分更高;在运行时间方面,由于轮廓线已经在断裂面提取过程中获取,没有增加太多额外计算,因此,运行时间与FPFH相当。 表2 “G1036”号兵马俑碎块拼接过程匹配得分Tab.2 The matching scores of Terracotta Warriors fragments labeled “G10-36” in reassembly process 然而,在某些情形下,本文提出的方法会暴露一些不足。如图9所示,由于碎块的断裂面严重破损(见红色框线内),特征信息不足,最终会导致匹配和配准的失败。 图9 断裂面严重破损示例Fig.9 An example of severely damaged fracture surface 本文提出了一种基于断裂面信息的文物碎块自动拼接方法。在匹配阶段,通过FPFH特征确定匹配点对,考虑到轮廓线的磨损,调整其对断裂面之间的匹配权重;在配准阶段,实现PCA方法中所有可能的方向,并根据断裂面之间的距离选择最优,解决了方向歧义问题;制作文物数据对DCP进行了迁移训练,并与PCA方法结合,完成由粗到细的配准过程。通过一系列实验,验证了本文所提匹配策略的有效性和配准策略的高精度与低开销,具体表现为:匹配得分提高了1到3,配准成功率达到53.89%,配准的平均绝对误差为0.920 2 mm。 然而,由于本文方法的特征来源和直接拼接对象均为断裂面,因此,具有一定的局限性。在断裂面保存比较完整的情况下,匹配与配准效果都能够实现预期结果;但是,在断裂面破损严重的情况下,结果不够理想。后续工作将会考虑如何在断裂面不完整的情形下完成文物碎块拼接任务。1.3 由粗到细配准


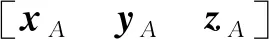
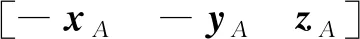
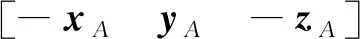
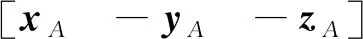


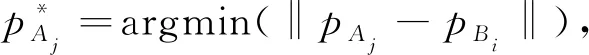
2 实验
2.1 实验说明
2.2 仿真实验


2.3 真实场景实验

3 结语
