船体型线三向光顺方法及程序设计
2021-06-28郑坤时光志周毅牛志刚
郑坤,时光志,周毅,牛志刚
(中海油能源发展股份有限公司 采油服务分公司,天津 300452)
船体型线设计对船舶阻力性能有直接的影响,决定了设计船能否达到航速要求。成功的型线设计的一个必要条件是型线的三向光顺。AutoCAD提供了良好的交互式图形设计工具,但是在船体型线设计时,AutoCAD不能将船体的三向视图联系起来,船体型线光顺过程只能对每个视图逐个修改,不仅繁琐,而且难以保证三视图数据的统一。为此,考虑采用AutoCAD提供的二次开发工具ObjectARX,通过型线的非均匀有理B-样条(NURBS)曲线表达及三次样条整体光顺方法,实现船体型线三向光顺程序设计。
1 船体型线的NURBS表达
NURBS曲线可以用统一的函数关系式表达直线段、圆弧和自由曲线。对直线段、圆弧及样条曲线进行拼接,就可以表达各种复杂的船体型线,其中涉及到关于NURBS的反算,升阶,节点插入与删除,求导,拼接等算法[1-2]。
船体型线较为复杂,可以基于NURBS曲线的优良特性,更准确的表达。船体横剖线对于艏部尾部线型比较复杂的情况,可采用自由曲线、直线段、圆弧等组合的NURBS曲线表达(见图1a)、b));对于有平行中体,且平行中体处舭部为圆弧的船型,将横剖线表达为由1/4圆与直线段组合NURBS曲线(见图1c))。对于有平行中体的船型,半宽水线由首尾圆弧(方尾尾部除外),自由曲线,以及平行中体处的直线段构成,见图2。
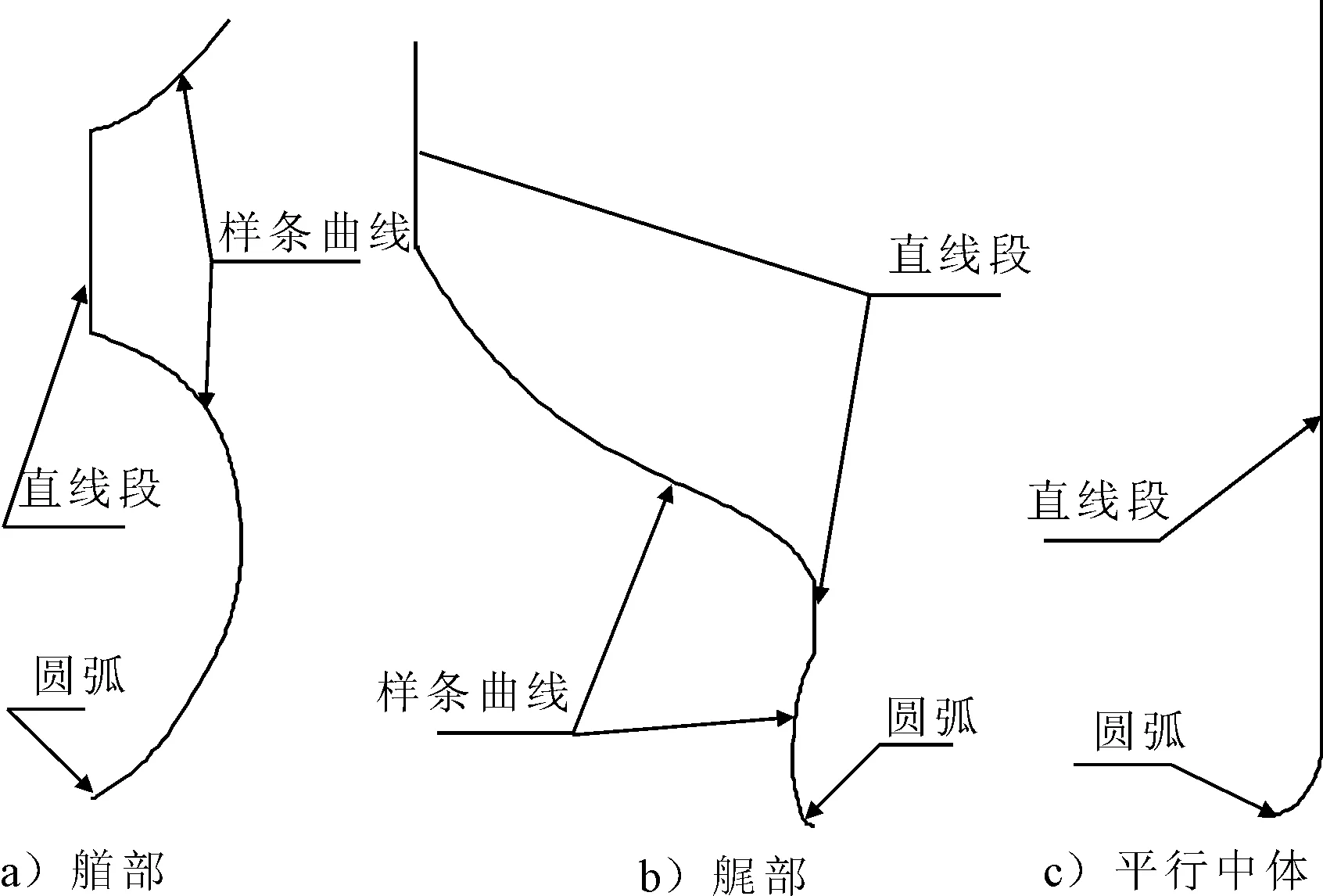
图1 用拼接的NURBS曲线表达横剖线

图2 半宽水线的NURBS表达
有些船型的首部轮廓在设计吃水与结构吃水之间为直线段,因而将其首部轮廓由直线和自由曲线拼接组成,见图3b),方尾船型的尾部轮廓由直线与自由曲线拼接组成,见图3a)。
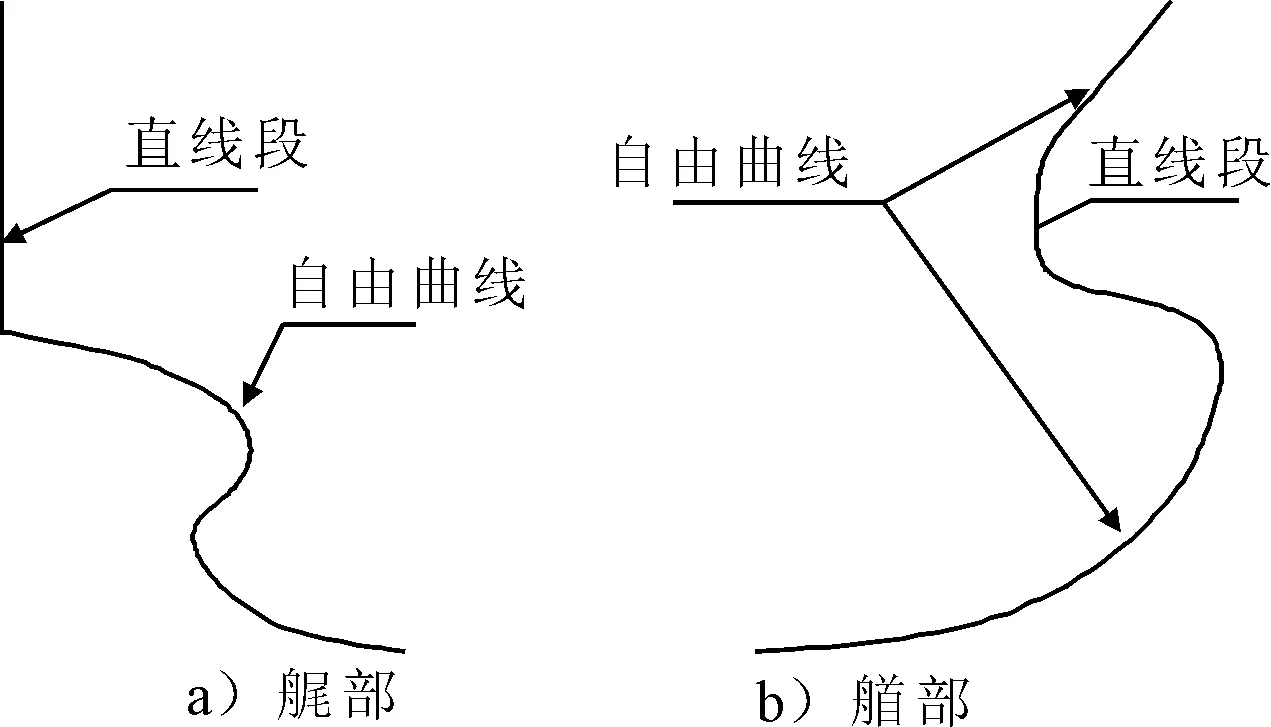
图3 艏艉轮廓线的NURBS表达
将各船体型线统一用NURBS表达以后,在对船体的计算时不用考虑是否间断或曲线的具体形状,因而更利于计算机程序实现。此外这样表示的型线更易应用于静水力、舱容、稳性插值曲线等的计算。
2 交互式三向光顺的程序实现
2.1 生成AutoCAD的NURBS曲线
ObjectARX提供了函数setNurbsData(),该函数的参数为NURBS的节点矢量(knots)、控制顶点(control points)、权值(weights)、节点数以及曲线的次数等[3]。创建AcDbSpline对象,调用该函数给实体赋值,并将该AcDbSpline对象添加到AutoCAD的当前数据库中,即可在AutoCAD里创建一条NURBS曲线。程序中定义了样条类class vacNurbs, 各种算法通过该类实现,将该类的节点矢量,控制顶点,权值等信息通过setNurbsData()函数传递给AutoCAD,由AutoCAD实现型线的交互式光顺。通过ObjectARX提供的函数getNurbsData()得到AutoCAD中的曲线信息,实现自己定义的样条与AutoCAD之间的数据交换。
2.2 实现三向光顺
三向光顺就是要在改变一个视图的时候,另外两个视图自动作相应的变化,即将3个视图联系起来,保持数据的统一。首先由ObjectARX的数据库反映者类(AcDbDatabaseReactor)派生出一个新类vacAcDbDatabaseReactor, 重载该类的objectModified()、objectAppended()以及objectEraserd()3个虚函数,用以响应数据库中实体被修改、添加与删除的消息。在程序初始化阶段将该反映者类的一个对象添加到当前数据库中,用于跟踪用户对AutoCAD的数据库的各项操作。
以修改横剖线为例。首先根据objectModified()的参数dbObj(被修改实体的ID)判断是哪条线被修改(假设为ST1,其纵向位置为stPos),给定精度为ESP=1e-6,然后根据由dbObj对应的曲线(修改后的横剖线)与原横剖线各型值点对比,判断哪些水线处的型值点变化量大于ESP(设为WL0~WL1),则这些水线需要重算。将对应的半宽水线WL0~WL1在stPos处的型值点替换为新的型值,重新反算生成新的半宽水线。纵剖线的变化与横剖线相似。这样就可以实现在修改横剖线时,半宽水线与纵剖线的自动变化。
同理,可以实现修改半宽水线时,横剖线与纵剖线随修改的自动变化。综上所述,便可以实现在AutoCAD平台上船体型线的三向光顺。
2.3 型线光顺性的检验方法
2.3.1 通过拐点数及位置判断型线的光顺性
如果船体的型线是光顺的,则相应的拐点连线也应该是光顺的,所以程序通过vacAcDbDatabaseReactor类的objectModified()函数在型线修改时计算出新的曲线的拐点所在位置,并绘制到型线图上,用来实时检验修改是否使型线更为光顺,见图4,“”代表拐点位置。
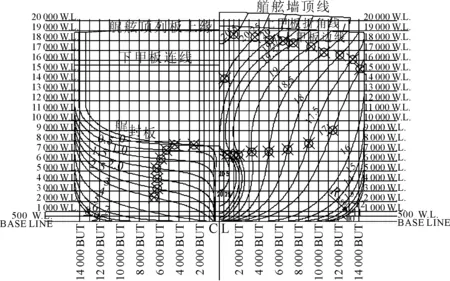
图4 某LNG运输船横剖线拐点示意
2.3.2 通过曲率曲线判断型线的光顺性
曲线的光顺与否将直接反应在曲率上,所以可以用曲率来检验型线是否真正光顺。图5中上方图形为型线,下方为该型线的曲率。
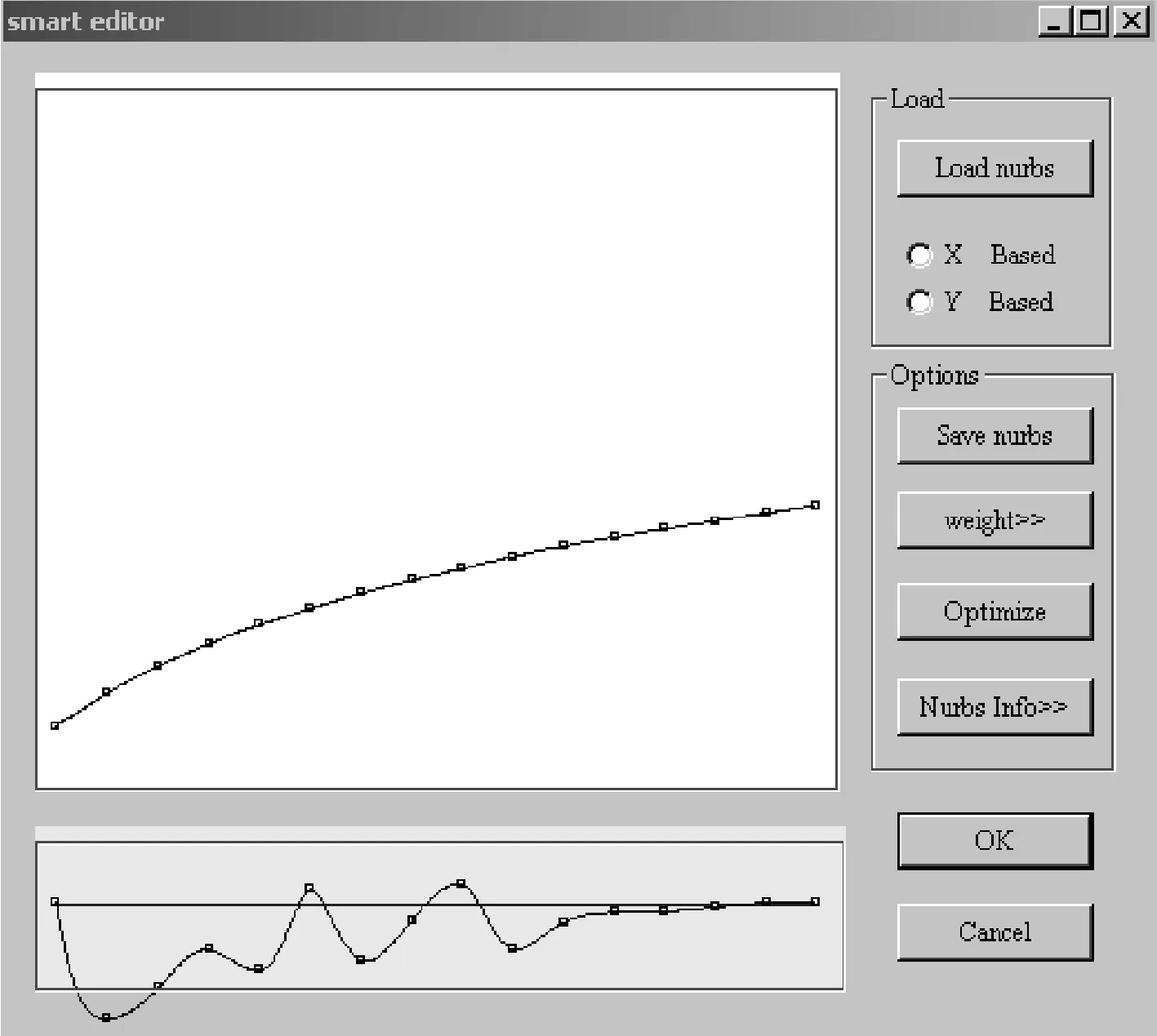
图5 NURBS曲线的曲率
3 船体型线整体光顺方法
型线整体光顺的方法有很多,传统的能量法和最小二乘法只能保证光顺后的曲线比未光顺的曲线曲率变化更均匀,而不易实现对曲线型值点位置、导数以及拐点的数目与位置的控制。这里在ObjectARX实现AutoCAD交互式三向光顺程序的基础上,引入一种可以控制曲线的型值点、一阶导数、二阶导数的型线光顺方法,以提升型线光顺效率。
3.1 三次样条整体光顺的思想
三次力学样条具有简洁的表达式,其二阶导数为线性关系式[4]。用三次力学样条可以很好的描述斜率变化不大的曲线。常规船型的半宽水线的斜率一般都不会太大,因而可以用三次样条来描述。基于以上原因,首先通过船体的半宽水线(NURBS曲线)形成一条三次样条,对该三次样条进行光顺,最后将得到的三次样条曲线的型值点作为新的半宽水线的型值点,反算得到光顺后的半宽水线(NURBS曲线)的控制顶点,进而实现对半宽水线的光顺。
采用单目标非线性约束优化的方法对三次样条做优化计算。将曲线的横坐标作为已知量,以各型值点的纵坐标和一阶导数为自由变量,以能量为目标函数,约束条件分为两部分,第一部分为固定约束,使得得到的纵坐标与一阶导数值之间满足三弯矩方程,另一部分为可变约束,用于控制曲线的型值点,一阶导数,二阶导数的值。
3.2 目标函数的建立
将三次样条看成梁,因弯曲而产生的内力为
(1)
式中:EI为梁的刚度系数;κ为曲率。
一般认为,梁的弯曲内力越小,样条越光顺[5]。但是内力最小的时候显然为1条直线,所以还要考虑因位移而产生的内力,即假定梁在每一节点处的受力与位移都满足hooker定律,即
(2)
式中:βi为各节点处刚性系数;Pi为光顺前的型值点;Qi为光顺后的型值点。
假设三次样条S(x)满足
S(xi)=yii=0,1,…,n-1
(3)
将目标函数定为E=Ein+Edisp,其中自由变量最高次项为2,线性约束,所以程序中采用二次规划对曲线进行优化,其目标函数为
s.t.

v=(y0,m0,y1,m1,…,yn-1,mn-1)
(4)
式中:nE与nI分别为等式和不等数约束个数;yi与mi分别对应各型值点处的纵坐标与一阶导数值。
3.3 约束矩阵的建立
3.3.1 固定约束
约束矩阵的固定部分即为三次样条的三弯矩方程组,是n-1个等式约束。三弯矩方程组为
(5)

将式(5)写成Am=f的形式,把y向量插入到v′向量中对应位置得到v向量,即v=(y0,m0,y1,m1,…,yn-1,mn-1),同时在A阵中插入相应的行与列。然后将等式右边向量移到等式左边,将gk用yk,yk+1表示,把gk中yk,yk+1的系数加到A阵的相应位置,形成约束矩阵R0v=b0,此时b0为零向量(即该约束为等式约束)。该约束矩阵保证生成的曲线为过点(xk,yk),并且在(xk,yk)处导数为mk。
3.3.2 可变约束
将约束矩阵添加一行,该行除了第2k列为1外全部为0,将向量b的与该约束对应的元素设为Y,并修改等式约束的个数,这样就可以使样条通过点(Xk,Y)。
若将该行除了第2k+1列为1外全部为0,将向量b的与该约束对应的元素设为D,并修改等式约束的个数,这样就可以使样条在点(Xk,Yk)处导数为D。
在xk处,二阶导数满足
(6)
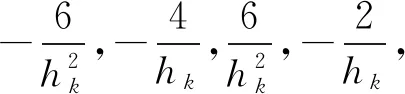
以上为加入等式约束的方法。加入不等式的方法与之类似,但要将大于号改为小于号(两边同乘-1)。将生成的约束矩阵交换行,使前nE个为等式约束,后nI个为不等式约束。
3.3.3 初始解的计算
二次规划要求初始解可行,因而不可以简单地将原样条对应的向量做为初始解。这里通过二阶段法求得。
3.4 在船体型线光顺中的应用
在光顺半宽水线时,首先要求输入期望的拐点位置。端点处要求型值不变,平行中体处要求导数为零,指定权值(用于调整光顺后曲线与原曲线的偏离程度)后程序就可以对所选的半宽水线进行光顺计算。只要输入正确的约束条件以及恰当的选取权值,该算法在满足光顺性的前提下可以很好的满足设计要求。对于多数的横剖线,只要将其x与y坐标转置,该算法也适用。图6、7为2个光顺实例。图中上方为型线,下方为曲率,其中变化缓和的为光顺后的型线的曲率。

图6 曲线中无指定拐点
3.5 算法的特点
若将型值点的权值设为一个相对较小的数,可以得到非常光顺的曲线,但是实际中的船体型线并非曲率变化越均匀越好,所以应当综合考虑,调整权值使得曲线在光顺后不会与原船体型线相差太大。对于有拐点的曲线,如果要求光顺后的曲线在某点处的曲率方向与原方向相反。优化的目标为弯曲内能与变形内能的和最小,此时优化的结果将是使该点处的二阶导数为零。如图7所示,通过下方的曲率图可以看出,中间竖线表示的期望拐点位置,曲线右端的曲率与期望的曲率方向相反,光顺后的曲线在此处曲率接近于零。如果在约束中指定这些点处的二阶导数的值可以控制曲率线的形状,但是事先难以估计该点处的二阶导数的值。
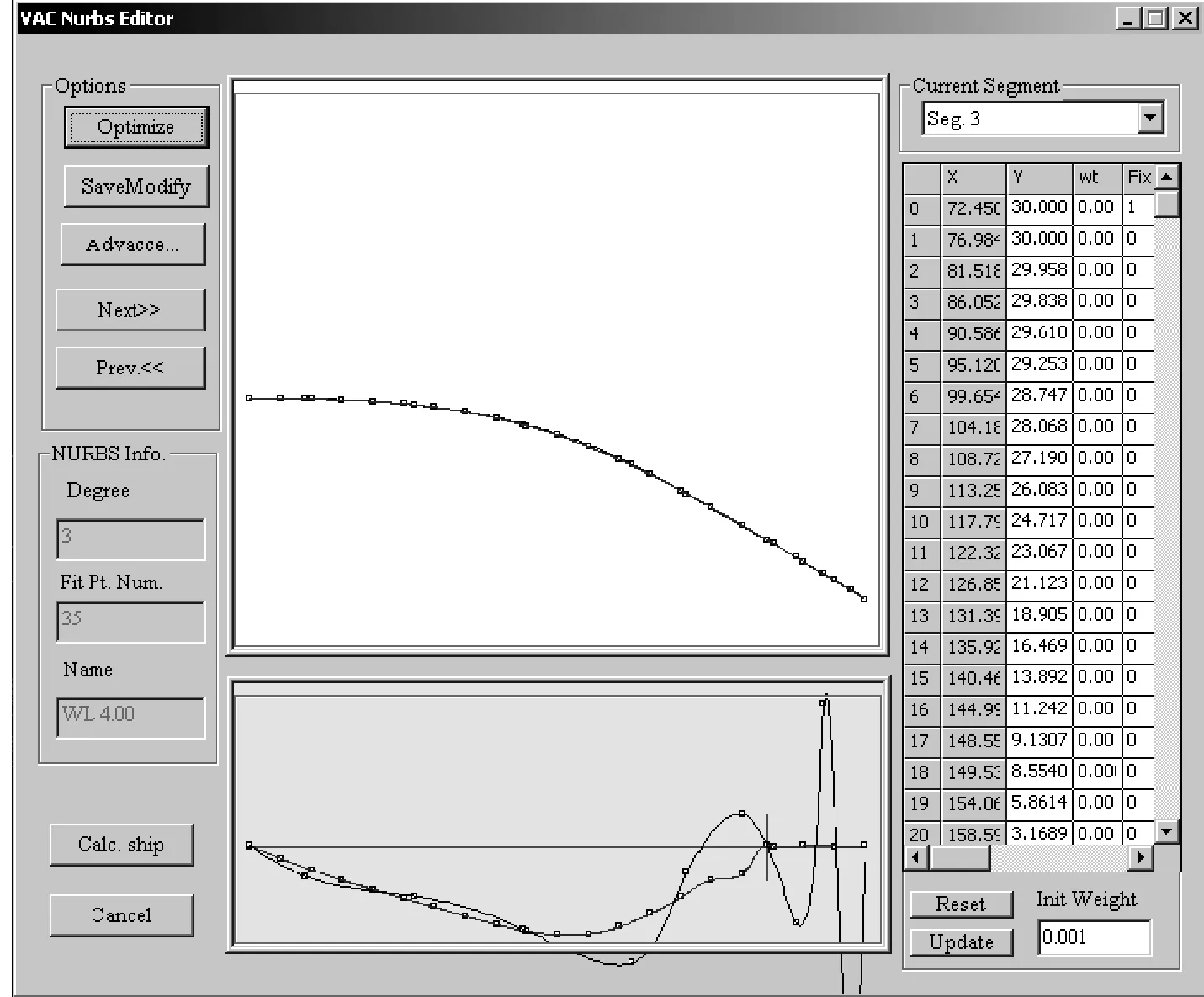
图7 期望的曲率方向与原方向相反
实践证明,上述方法能够快速、准确的实现船体型线的三向光顺,这不仅可以提高的型线设计的效率,而且可以保证精度要求。实船型线光顺的实例见图8~11,图中“”代表拐点位置。通过拐点数及拐点的位置,可以看出曲线的光顺程度。

图8 某LNG运输船光顺前的艏部型线

图9 某LNG运输船光顺后的艏部型线
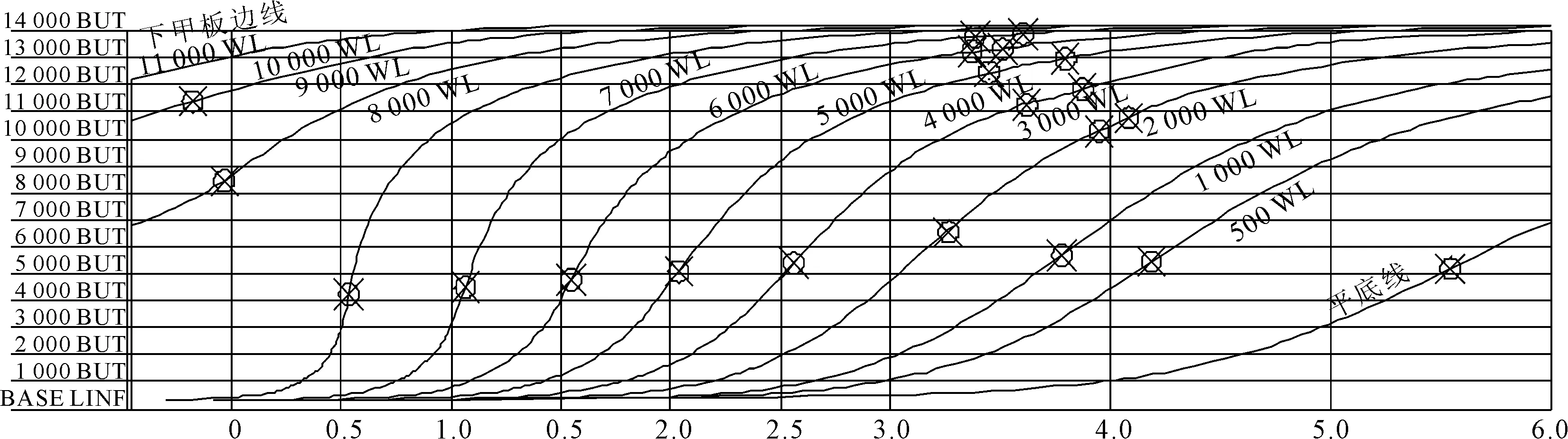
图10 某LNG运输船光顺前的艉部型线

图11 某LNG运输船光顺后的艉部型线
4 结论
1)采用拼接NURBS曲线表达船体型线不仅使得计算简单,易于程序实现,而且可以较为精确的描述船体型线,有利于对船体做进一步计算。
2)AutoCAD平台提供了有效的二次开发方法,通过对AutoCAD二次开发可以实现船体型线数据的三示图联动,并形成基于拐点和曲率曲线的光顺性检验方法。
3)以三次力学样条为工具,可以很好的实现对NURBS曲线的光顺,提升型线光顺效率,解决型线光顺繁琐的调整问题。
