主动配电网分布式电源规划分析与研究

李彦生

（大理供电局，云南大理 671000）

传统配电网网络规模扩充困难，空间资源受限，电网负荷的快速增长已难以满足分布式能源的大量接入要求，因此传统配电网需向主动配电网转型[1]。采用发电侧与需求侧的协调优化，提升可再生能源利用率，通过大量分布式能源的接入并网，提升经济价值[2]。

主动配电网是由分布式电源、负荷及储能设备等构成的微网系统[3]。目前，相关研究者对其分布式能源规划进行了大量研究。文献[4]将运行成本、利润及用户用电作为目标，优化储能系统容量，但其目标配置单一，无法从全局对配电网的规划情况进行分析。文献[5]通过改变配置方式规划主动配电网的分布式能源，但只是对调度计划因素或最小排碳量进行了优化，未考虑规划的经济效益。

基于以上研究，文中对主动配电网各分布式能源进行规划，建立多目标优化模型。模型中以线损、储能调峰及发电成本作为优化目标，以功率平衡为约束条件，结合粒子群算法、自适应遗传算法进行模型求解，以提高分布式系统容量配置的合理性。

1 理论基础研究

当前，我国电网采用将用户串联成环的方式进行架设，该种形式确保了一侧发生故障时，仍可为用户供电，增加了电网运行的可靠性[6]。将由可控负荷、分布式储能及发电组成的微网系统接入配电网，增加了系统架构和操作的灵活性、便捷性，提高了系统的安全性，具有容易扩容的优势，适用于并网和孤岛两种运行模式[7]。

文中以中低压配电网为研究对象，其主动配电网环网接线方式如图1 所示。

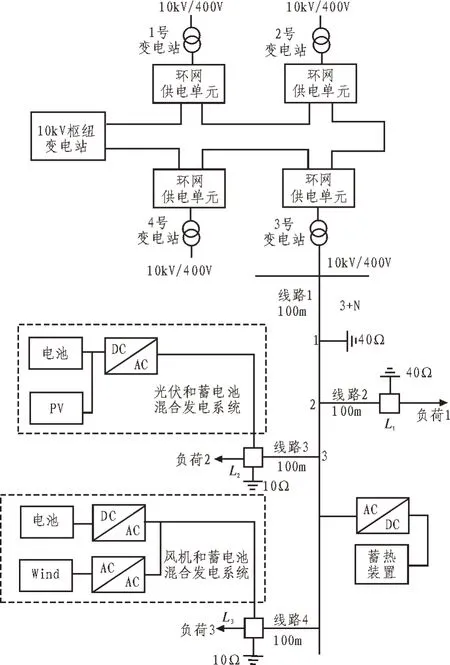
图1 主动配电网环网接线示意图

图1 中，分布式能源由风机、光伏两种发电形式构成，可控负荷为3 处。文中基于环网配电、线路损耗及负荷预测对某供电单元分布式能源进行合理规划，以确保系统运行的经济性、可靠性。

1.1 分布式能源数学模型建立

1）光伏系统

忽略线路损耗等因素，理想状态下光伏发电功率[8]为：

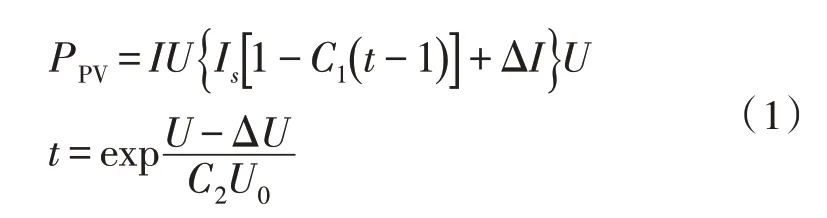
式中，U为阵列输出电压；I为工作电流；U0、Is分别为参考温度及日照强度下的开路电压及短路电流；C1、C2分别为与功率跟踪点开路电压及电流、短路电流相关的常数；ΔU、ΔI分别为环境温度及日照强度变化时的修正电压及修正电流。

2）风力发电系统

风力发电机组输出功率[9]为：

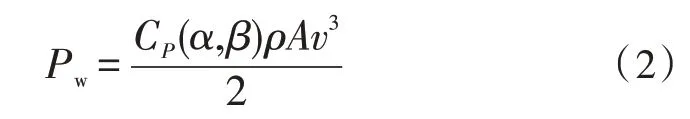
式中，A、Pw分别为风轮扫掠面积及输出功率，A=πR2；β、R分别为桨距角及风轮半径；ρ、v分别为空气密度及风速；α为叶尖速比；CP为风能转换系数。

3）储能系统

由于变流器系统及电池容量限制，储能系统相邻时间段的能量[10]为：

式中，η+、η-分别为充电、放电功率，其与放点深度、环境温度及内阻相关；ξ为储能系统自放电率，与电池内部特性相关；E(t)为储能系统前一时刻能量；分别为第i时间段系统的储存功率、释放功率。

1.2 负荷预测

恒阻抗负荷、恒电流负荷及恒功率静态负荷为配电网负荷的主要形式。在配电网规划中，通过削峰填谷来降低分布式能源的容量需求[11]。基于负荷曲线，负荷趋势可划分为友好型负荷Pg及峰值负荷Pmax，以满足用户基本用电需求及用电最大值需求。

基于负荷需求相关性分组，确保各分组内负荷需求相似。不同时间负荷需求相关性分组-多时间点预测流程如图2 所示。

图2 需求相关性分组-多时间点预测流程图

基于主动配电网一年内各时间段的负荷需求相关性，建立主动配电网系统。统计本地一年内线性、非线性负荷，并选定负荷量Pf0居中的月份，对比各月负荷量Pf，Pf≤Pf0±50%。以Pf0为参考值，统计各月负荷值与参考值之间的偏差若测量负荷值则该负荷为友好型负荷，反之为非友好型负荷。

基于相关性分组-多时间点预测，通过K-mean聚类分析，根据负荷约束形式，提升分布式能源规划精准性。

2 主动配电网规划方法研究

2.1 安装位置优化

分布式电源包含光伏、风力发电机组等受位置及地理环境影响较大的新能源发电装置，假设安装位置为风资源及光资源的最佳接受位置。由于确定安装位置时应综合考虑线路损耗问题，因此所建立目标函数应对此充分考虑。线路损耗规划中包含将电网输送功率向电费损耗量的折算及无功功率、有功功率损耗量[12]。

单运行周期中馈线损耗Ploss为:

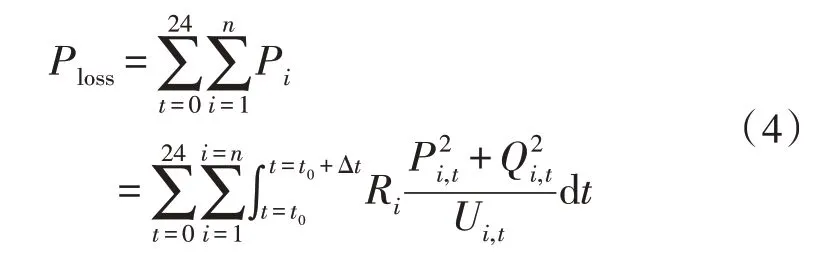
式中，Pi为第i馈线于Δt时刻的功率损耗值；t0为初始时刻；n为总馈线量；Ri为第i馈线的电阻值；Qi,t、Ri,t、Ui,t分别为第i馈线于Δt时刻的无功功率、有功功率及支路电压值。

线路损耗向电费损失f1折算为:

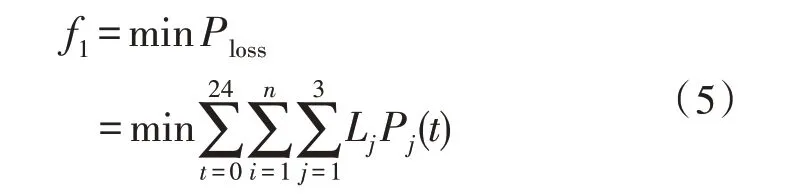
式中，Lj为各时刻电价成本；Pj(t)为t时刻第i馈线的功率损耗。

2.2 分布式能源规划

在分布式能源规划中，综合发电成本，设定分布式能源目标函数[13]，即：

式中，fPV为光伏发电成本；fw为风力发电成本；x为风力发电机个数；ax为单位风力发电机造价；Pwx为单风力发电机功率容量；L(Pwx)为风力发电机组折旧及年维修费用；r、φ为贴现率；PPVy为光伏发电功率容量；by为光伏发电单位造价；l为利率；L(PPVy)为光伏系统折旧及年维修费用。

2.3 储能系统容量规划

储能系统能量优化可削峰填谷、平抑输出功率，提高系统稳定性。文中综合考虑峰谷电价差，以加入储能系统的主动配电网经济性为优化目标，对储能系统容量进行配置。

储能设备购进成本C0为固定值，运维成本每年按照比例上涨，储能系统整个寿命周期所产生的经济效益[14]为：

式中，Cr0、Cri分别为第一年及第i年运维成本的增长；分别为第i时刻用电高峰期及用电低谷期电价；β为增长系数；k为年投运天数；C为初始投入成本及运行成本和；C/k为储能系统折算后单天成本。

2.4 多目标优化

综合考虑运行成本、位置优化、线路损耗及储能经济配置，进行多目标优化，优化目标函数[15]为：

式中，c1、c2、c3为权重系数，且c1+c2+c3=1，根据优化侧重不同，选取对应权重系数。

约束条件包含蓄电池不越限，储能系统满足负荷要求，功率平衡等，即

式中，Pload为整体负荷；Pout为输出供给功率；PES_in、PES_out分别为储能系统充电及放电功率；Pin为需要输出功率；Ec_i、Pe_i分别为第i个储能系统单元容量及功率；Nmax为允许充放电次数最大值；Lc(i)、Ld(i)分别为第i个时间段连续充电和连续放电次数；分别为i时段储存功率及j时段释放功率；η为充电效率。

下标PV、w、load、c 分别表示光伏系统、风力发电机组、负荷及储能系统。

2.5 多目标求解

在分布式能源规划中，通过权重及自适应泛函数的遗传算法进行多目标求解[16]，即：

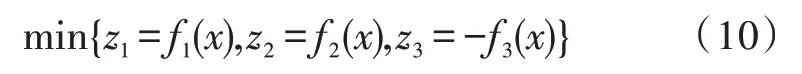
z1、z2、z3为通过遗传算法对多目标进行优化后的函数。

为将全部目标函数转变为最小化问题，需将储能经济收益最大化目标进行取负处理。对于各既定个体x，其权重为：

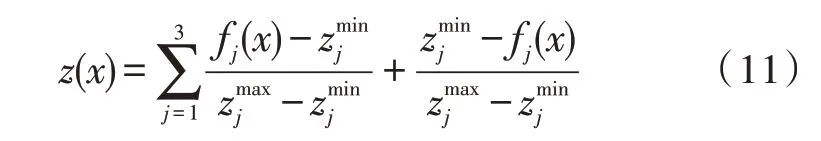
式中，i为种群染色体编号；max、min 分别对应函数取最大、最小值。

为有效地归一化处理目标函数权重，将式（11）中每个目标函数的个数同时减对应式（8）的c1、c2，对应c3。

式（8）优化目标函数可转变为

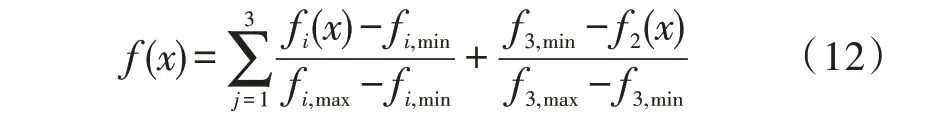
规划求解主动配电网分布式电源时，通过自适应遗传算法配置各分布式电源位置、容量，确保整个局域配电网的安全性和经济性。

3 仿真分析

为了对文中规划方法的有效性进行验证，依据某地实际负荷进行负荷预测，并对主动配电网构架下的分布式能源进行规划。基于该地区实际负荷，结合需求相关性分组及多时间点预测的方法对负荷侧进行预测，获得本地负荷数据均值和峰谷差负荷数据最大值，如图3 所示。

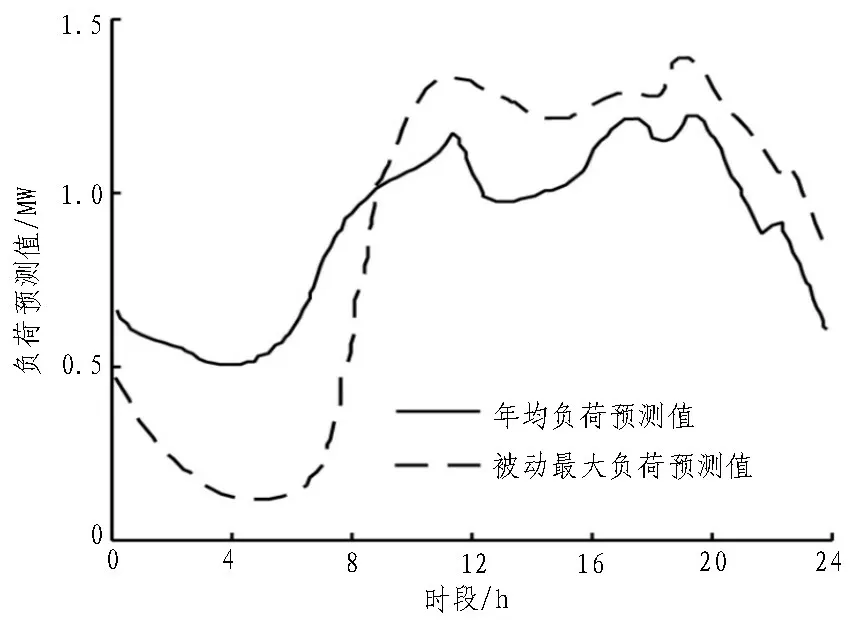
图3 某地实际负荷预测结果

由图3 可知，该区域每天分别于11:00、17:00 及19:00 出现3 次负荷高峰，各高峰持续时间分别为2.5 h、3.5 h、2.0 h，且于11:30 及17:00 出现负荷峰值。基于负荷预测，合理配置各分布式能源容量。通过IEEE-RTS 24 总线系统进行实例分析，其中并网节点为节点3，其他节点为负荷节点，根据图3 预测结果对节点8 加载负荷数据。

基于各节点负荷需求，综合分析分布式能源运行成本的经济性、储能经济性及线路损耗，确定储能系统安装位置及系统容量，确保整个区域配电网运行的经济性。不同节点分布式电源配置如表1所示。

由表1 可知，风力发电系统安装于节点2、18、23；光伏发电系统安装于节点7、15、21；储能系统安装于节点1、22。各节点设备容量为200～800 kW。

表1 不同节点分布式电源配置

以节点8 所配置分布式电源为例进行分析，根据储能和负荷的工作情况，计算运行的经济性和弃风、弃光量。不同运行模式及结果分析如表2 所示。

表2 不同运行模式及结果分析

由表2 可知，负荷波动情况随储能状态的变化而变化，致使储能系统运行费用发生变化，同时产生一定程度的弃风、弃光。

4 结论

为提高主动配电网供电的经济性及可靠性，增加分布式能源利用率，文中对电源规划方法进行了研究。通过需求相关性分组预测负荷，并基于预测结果规划分布式能源，同时充分分析线路损耗、分布式能源发电成本、储能系统运行的经济性等因素，实现储能系统各分布式电源的选址与定容，为主动配电网扩容及规划提供了理论依据和方法。