小半径曲线刚构桥动力特性分析
2021-06-27秦亮
秦 亮
(甘肃省交通规划勘察设计院股份有限公司,甘肃 兰州 730070)
1 工程概况
某小半径曲线刚构桥,主梁为预应力混凝土单箱单室箱梁,跨度组合为32m+32m+32m。梁宽10.0m,底板宽2.0m,悬臂板宽2.5m,梁高2.0m。边墩附近设置2.4m 过渡段,腹板厚由0.61m 过渡至0.51m,底板厚度由0.42m过渡至0.25m,顶板厚0.25m[1]。其墩顶截面尺寸如图1 所示。

图1 墩顶截面尺寸
2 有限元模型的建立
采用Midas Civil 2019 有限元软件建立全桥空间模型,共划分117 个单元,121 个节点。1#、4#墩顶设单向活动支座,与主梁通过主从节点连接,2#、3#墩与主梁固结[2]。建立的空间有限元模型如图2 所示。

图2 有限元模型
3 动力特性分析
3.1 曲率半径对自振频率的影响
以上述曲线刚构桥为例,保证结构其它尺寸不变,只改变曲率半径,建立曲率半径为R=60m、180m、300m 和∞等4 个模型[3]。采用Midas Civil 2019有限元软件对每个模型进行自振频率分析,结果见表1。

表1 曲线刚构桥的自振频率(Hz)
由表1 可知,随着振型阶数的升高,曲线刚构桥自振频率逐渐增大,曲率半径对曲线刚构桥自振频率的影响不大,特别是对基频的影响小于1.23%;曲率半径为180m 时曲线刚构桥前4 阶振型如图3 所示。

图3 曲线刚构桥前6 阶振型
由图3 可知,随着振型阶数的增加,小半径曲线刚构桥的振型规律性减弱,且结构振动主要以竖向弯曲为主。
3.2 曲率半径对顺桥向地震作用下结构内力影响
以上述曲线刚构桥为例,选取该桥1#和2#墩支座连线方向为顺桥向方向,以此作为基准,输入顺桥向地震波[4],研究曲率半径为R=60m、180m、300m 和∞等4 个模型中2#墩内力变化情况,结果见表2~3。
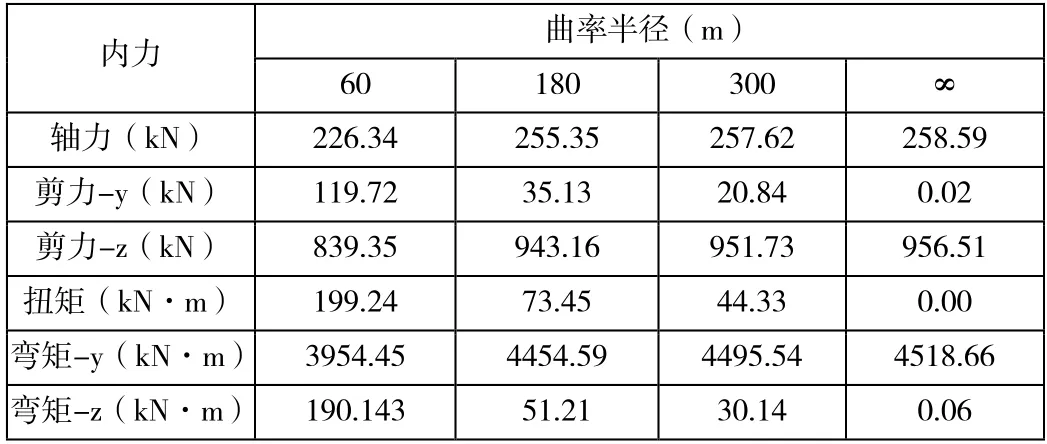
表2 顺桥向地震作用下2#墩顶内力
由表2 可知,随着曲率半径的增大,2#墩墩顶的-y 方向剪力、扭矩和-z方向弯矩逐渐减小,曲率半径小于180m 时,2#墩墩顶的轴力、-z 方向剪力、-y 方向弯矩呈现增长趋势,当曲率半径大于180m 时,这种趋势又表现得比较缓和。
由表3 可知,随着曲率半径的增大,2#墩墩顶的-y 方向剪力、扭矩和-z方向弯矩逐渐减小,各数值的变化趋势和2#墩顶内力变化情况类似。

表3 顺桥向地震作用下2#墩底内力
3.3 曲率半径对横桥向地震作用下结构内力影响
同样以上述曲线刚构桥为例,选取该桥1#和2#墩支座连线方向为顺桥向方向,以此作为基准,输入横桥向地震波,研究曲率半径为R=60m、180m、300m 和∞等4 个模型中2#墩顶内力变化情况,结果见表4。
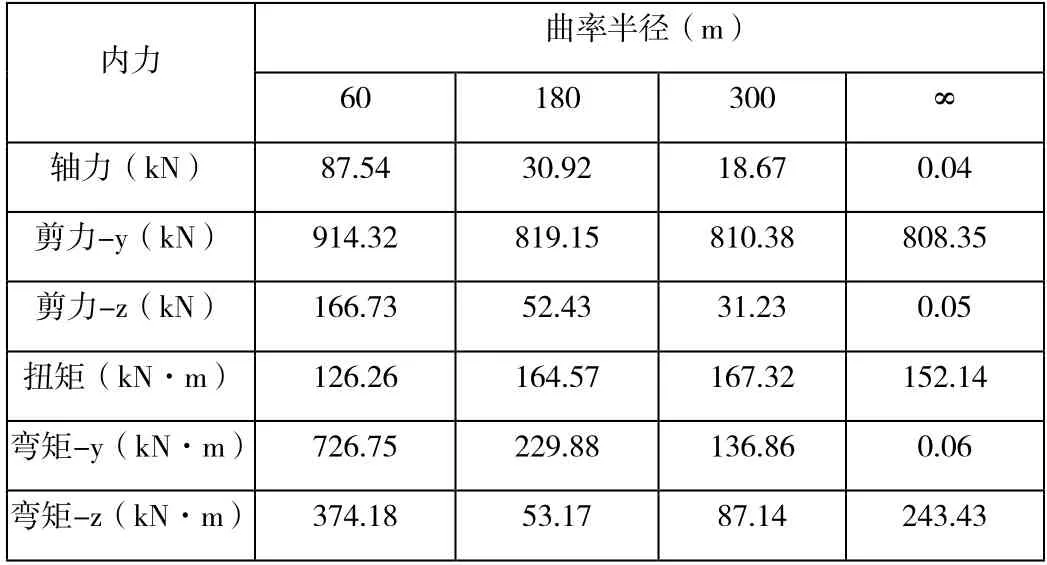
表4 横桥向地震作用下2#墩顶内力
由表4 可知,在横桥向地震作用下,当曲率半径增大时,2#墩墩顶扭矩先增大,然后又逐渐减小;而-y 方向弯矩减小的非常明显,当曲率半径等于∞时,-y 方向弯矩接近等于0;-z 方向弯矩呈现先减后增的变化规律。
3.4 不同地震方向作用下结构内力分析
地震波传播的方向具有随机性,要使结构内力达到最大,则地震波激励需沿着一定方向[5]。为研究地震波传播方向对结构内力的影响,以上述曲线刚构桥为例,地震波以0°、60°、120°和180°方向对结构激励[6],分析不同地震方向作用下结构内力的变化情况,结果见表5~6。

表5 不同方向地震波作用下2#墩墩顶内力
由表5 可知,当地震波输入方向增大时,墩顶位置-z 方向剪力和轴力先减后增,地震波输入角度为0°时达到最大值;横向剪力的变化趋势与之相反,地震波输入角度为0°时达到最小值。
由表6 可知,当地震波输入方向增大时,墩底位置-z 方向弯矩先减后增,地震波输入角度为0°时达到最大值;-y 方向弯矩的变化趋势与之相反,地震波输入角度为0°时达到最小值;但是,无论以何种角度对曲线刚构桥进行激励,2#墩墩顶底力均可相应条件下达到极值。

表6 不同方向地震波作用下2#墩墩底内力
4 结论
通过对此小半径曲线刚构桥进行动力特性分析得到以下结论:
(1)随着振型阶数的升高,曲线刚构桥自振频率逐渐增大,曲率半径对曲线刚构桥自振频率的影响较小。
(2)随着振型阶数的增加,小半径曲线刚构桥的振型规律性减弱,且结构振动主要以竖向弯曲为主。
(3)当曲率半径大于180m 时,#墩墩顶的轴力、-z 方向剪力、-y 方向弯矩增长趋势相对比较缓和;在横桥向地震作用下,当曲率半径等于∞时,-y 方向弯矩接近等于0;-z 方向弯矩呈现先减后增的变化规律。
(4)无论以何种角度对曲线刚构桥进行激励,2#墩墩顶和墩底内力均可在相应条件下达到极值。
