Wave packet dynamics of nonlinear Gazeau–Klauder coherent states of a position-dependent mass system in a Coulomb-like potential
2021-06-26FaustinBlaiseMigueuMercelVubangsiMartinTchoffoandLukongCorneliusFai
Faustin Blaise Migueu Mercel Vubangsi Martin Tchoffo and Lukong Cornelius Fai
1Unit´e de Recherche de Mati`ere Condens´ee,d’´Electronique et de Traitement du Signal,D´epartement de Physique,Facult´e des Sciences,Universit´e de Dschang,B.P:67,Dschang,Cameroon
2Computational Material Science Laboratory,Higher Technical Teachers’Training College Bambili,University of Bamenda,PO Box 39,Bamenda,Cameroon
3Centre d’´Etudes et de Recherches en Agronomie et en Biodiversit´e,Universit´e de Dschang,Dschang,Cameroon
Keywords: deformed Coulomb potential,energy spectrum,coherent states,photon number distribution,quan
1. Introduction
We have known for a long time that in semiconductor lattices, charge carriers such as electrons or holes behave as if their masses have been altered, compared to their vacuum masses. The so-called effective mass possesses anisotropy,and it sometimes appears to be negative.[1–7]The study of effective masses has gained importance in recent times,because the control of semiconductor materials is the origin of modern information and communications. Due to the recent development of devices that exhibit interesting quantum effects,physical systems with variable masses have emerged. In particular,systems with position-dependent masses play a major part in quantum wells,heterostructures,inhomogeneous doped semiconductors,quantum liquids,graded crystals,nanoscale quantum rings, etc.[8]Nevertheless, the quantization of such systems encounters serious mathematical challenges,due to complexity encountered during the resolution of eigenfunction equations. More precisely, the task of prospective generalization of the standard hamiltonian using variable mass theory is made difficult by the fact that the momentum and mass operators do not commute. A number of physical variablemass scenarios exist. An illustrative case has been pointed out by Wanget al., who provided evidence that the Schr¨odinger equation for a thin charged envelope moving in an appropriate gravitational field can be likened to a coordinate-dependent mass problem.[9]The literature overflows with techniques for investigating such problems. Among them,one can cite point canonical transformation, factorization by the supersymmetry method,the displacement operator approach,Lie algebraic parametrization, the Nikiforov–Uvarov method, the path integral approach,etc.[10–14]The commutation relation between the position operator and the momentum induces ordering ambiguities in the kinetic energy operator, giving rise to various forms of hamiltonian, as shown in Refs. [15–19]. The history of quantum mechanics is long and deep, but the comprehension of singular potentials remains less extensive. This is the case forD=1 Coulomb problemsx−1, for which, all solutions should satisfy the wave equation over the whole of thex-axis, including the origin. The results of this class of problem are significant, theoretically as well as experimentally,although the literature abounds with related controversial statements.[20–26]Quantum mechanical systems with variable masses are not yet mastered, although voluminous research has been conducted on the subject. A hot topic for experts is the limit between classical mechanics and quantum physics.In the early days of quantum theory, this question was investigated by Erwin Schr¨odinger, who established a correspondence between classical and quantum dynamics with a minimum uncertainty using the framework of the harmonic oscillator. However, he did not extend this minimum uncertainty to all physical systems. After a period of hibernation of more than three decades,Roy Glauber had the ingenious idea of expressing these minimum uncertainty states in terms of the raising and lowering operators of the harmonic oscillator.[2,3,27,28]These states were given the name coherent states and then generalized to systems much more complicated than the harmonic oscillator in various fields of physics,such as quantum electrodynamics, quantum optics, quantum processing, quantum information and computation, etc. In most textbooks today, one comes across the following definitions of coherent states: (i) eigenstates of the lowering operator; (ii) states resulting from the displacement operator’s action on the vacuum;(iii)states that minimize the Heisenberg–Robertson uncertainty relation and (iv) states that satisfy Gazeau–Klauder natural conditions by constituting an overcomplete family of vectors in the Hilbert space of the harmonic oscillator.[29–32]Coherent states of this fourth class are recognized to fulfill the temporal stability and action identity conditions. In Ref.[29],it is emphasized that Gazeau–Klauder coherent states have emerged as the most important for the analysis of physical systems and should survive if one puts aside coherent state properties. In this work, we focus on Gazeau–Klauder coherent states which have previously been studied for constantmass systems, but have not yet captivated the attention of researchers for use in variable mass systems, apart from a few scientific publications.
This paper is structured as follows. In Section 2, we start by presenting the model of the studied system, the energy eigenvalues and also the bound state eigenfunctions of the underlying system; Section 3 is devoted to the generation of Gazeau–Klauder coherent states and an investigation of their basic properties by means of the probability distribution of photons in the configuration space; the main purpose of Section 4 is an inquiry into some aspects of the previously constructed coherent states during their time evolution. We end this communication by summarizing our results in Section 5.
2. System model and generation of the energy eigenvalues
2.1. Derivation of the energy spectrum
In the context of semiconductor heterostructures, unidimensional position dependent mass Schr¨odinger equations were proposed in the 1980s,based on von Roos’idea and set up in terms of ambiguity numbersa1,a2anda3constrained asa1+a2+a3=−1,that is,[33]
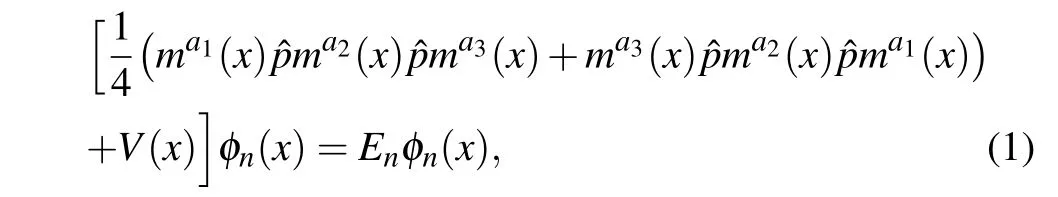
where the momentum operator=−id/dx,Enis the energy spectrum of the system under consideration andφn(x)denotes its eigenfunctions, which provide us with the probability amplitude for the charge carrier to be at a positionxalong the axis.V(x)stands for the potential that describes the space in which the studied quantum particle evolves. One can write another closed form of, the momentum operator, so that the equation becomes[34]

It is possible to connect Eq. (2) with the von Roos kinetic energy operator presented in the coordinate dependent mass Schr¨odinger Eq. (1) through a hermitization scheme introduced by Mustafa-Mazharimousavi,[35]leading to the ordering ambiguity parameter set ofa1=a2/2 =a3=−1/4.Our particle, investigated hereafter, is designated as a space variable-effective-mass charge carrier with an effective mass expressed by the following numerical law:
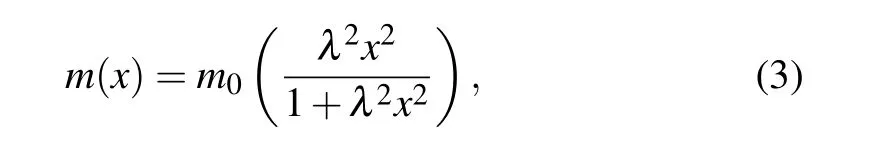
in whichm0is the carrier vacuum mass andλrepresents the space deformation coefficient with the inverse length dimension.This gauges the accuracy of the link between the carrier’s effective mass and the coordinate. We assume this charge carrier to be moving in a quantum space modeled by a Coulomb–type potential given by
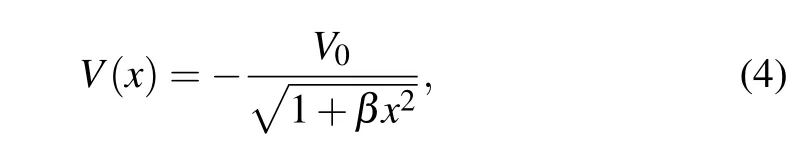
in which the singularity has been lifted off, compared to the standard Coulomb one. Theβ-parameter with a squared inverse length dimension evaluates the impact of the coordinate on the potential. Such an alteration in the potential renders the problem more realistic, as well as bypassing the troublesome Dirichlet conditions.[36]The idea here is to model the system with a renormalized form of the Coulomb potential which is physically easier to implement. Fig. 1 is a plot of the mass profile as well as the variations of the quantum potential defined by Eq.(4).From curve(i),it can be seen that the carrier’s effective mass is zero at the coordinate origin,but equal to the vacuum mass when the particle is distant from that position.Such a situation is recurrent in heterostructures. In the case of curve (ii), the particle experiences a potential with fewer impurities than in case(iii). With fewer impurities,the carrier moves more freely along the chain. It is worth pointing out that the more impurities,the deeper the potential well. Such a potential has been studied in Ref. [37] using soliton features in doped trans-polyacetylene (CH)v, assumed to be a matrix of parallel linear chains with no inter-chain conduction. To generate the bound states of the system in theβ=λ2scenario,let us substitute Eqs.(3)and(4)into Eq.(2)and then perform the following independent variable changes:

Fig. 1. Plot of the mass function (i) and the confinement potentials V0 = 1 (ii), V0 = 2 (iii) versus the position of the charge carrier for β =0.64,λ =0.80 and m0=1.
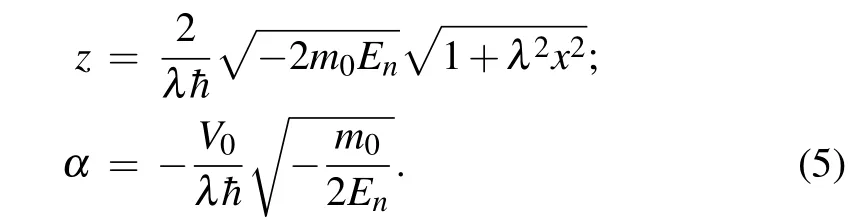
It follows after careful calculation that the Schr¨odinger wave equation(2)is equivalent to
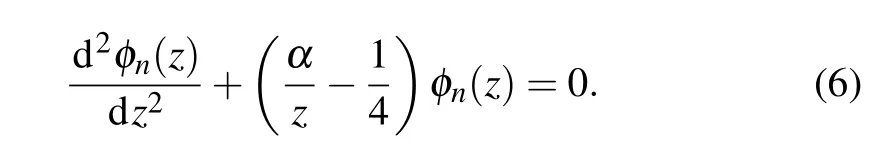
By taking into account the asymptotic behavior of the energy eigenvector solutions of Eq. (6) forz ≫1, we choose the ansatz
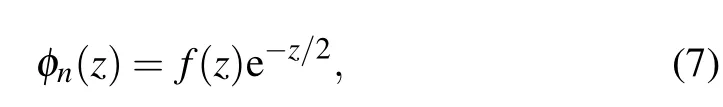
resulting in Kummer’s equation
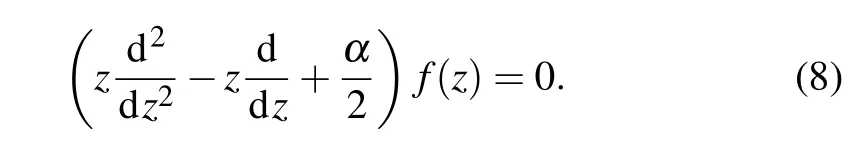
Equation(8)is solvable only if the parameterαis constrained to be an integer[38,39]. Sincef(z) is expected to be a single hypergeometric function1F1,thereforeα=n+1,n=0,1,2,etc. Consequently,Eq.(5)yields
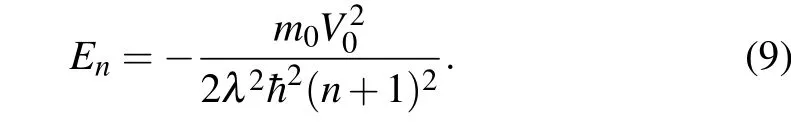
The result of Eq. (9) is satisfactory insofar as it is consistent with the 1/n2dependence of the energy spectrum previously seen in many other Coulomb problems.[20,22,26,40–44]Furthermore,one notes that these energy eigenvalues are proportional to the strengthV0of the confinement potential but,are scaled down by the space deformation coefficientλ. Let us use the analytic procedure to solve Eq.(8).
2.2. Traditional method to complete solutions
We assume the solutionf(z)as the Frobenius series
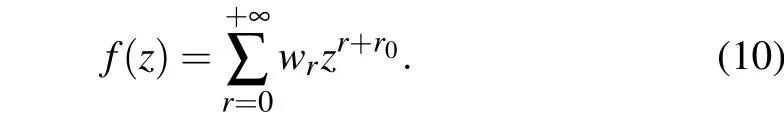
The motivation for choosing the Frobenius approach is that the numberr0can be zero or any rational number. The first and second derivatives of Eq. (10) with respect toz, carefully introduced into Eq.(8),provide us with the following recursive relation:
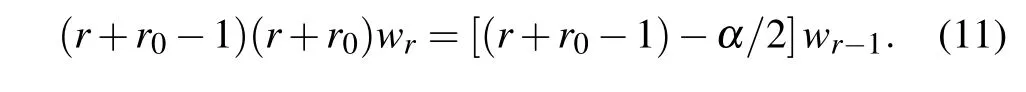
It can be seen that the lowest power ofzis derived fromr=0.Thus,r0(r0−1)=0. The caser0=0 has been put aside,since it leads to meaningless terms. Thus,

appears as a suitable solution. Trying few iterations,
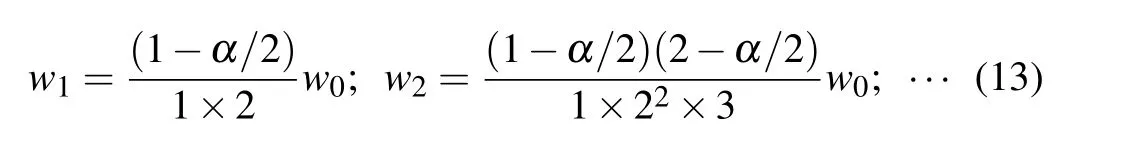
leads to the following general coefficient:

that permits Eq.(10)to yieldf(z)as

which exactly matches our expectation off(z) being a1F1confluent hypergeometric function. Equation(15)can then be introduced into Eq.(7)to finally give the general solutions of the wave equation as

The eigenfunctions of coordinate spaceφn(z) admit the following boundary conditions:
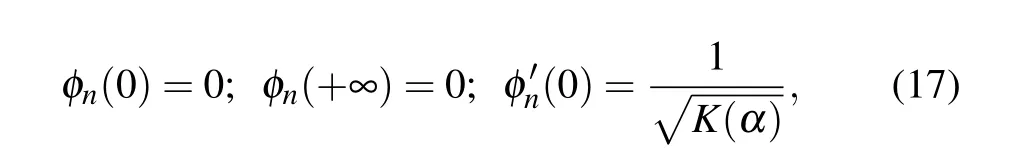

An alternative approach would be to consider a deformed space
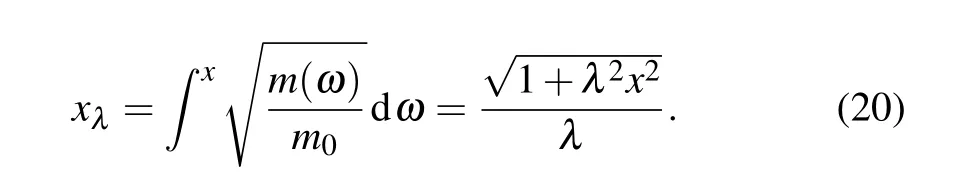
Thus, the transformationx →xλchanges the problem of a charge carrier with variable mass trapped in a deformed potential (4), into that of a charge carrier with a constant-mass confined in a standard Coulombian potential,say
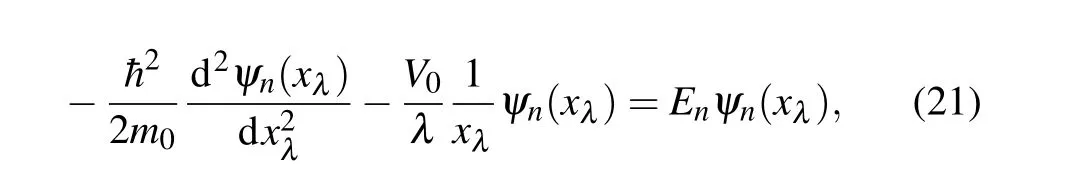
withψn(xλ) =φn(x(xλ)). The solutions of the onedimensional problem stated in Eq. (21) have been discussed in Refs.[46,47]in terms of the associated Laguerre polynomialsL(ν)n

The solutions to problems (4) and (21) are isospectral. This view gives a physical meaning to the deformed 1D Coulomblike problem studied. In addition, the solution given by Eq.(22)permits a compact form of the normalization constantK(n) to be obtained by means of the orthogonality condition of the associated Laguerre polynomials.
We now have sufficient materials to build coherent Gazeau–Klauder states in Section 3 of this communication.
3. Coherent Gazeau–Klauder states of the system and their properties
3.1. Generation of Gazeau–Klauder coherent states
Unlike other coherent states such as Barut–Girardello’s or Perelomov’s which are constructed on the basis of Lie groups,Gazeau–Kauder coherent states are not associated with any algebraic group. For any Hermitian Hamiltonian of eigenstates|φn〉, the unique cornerstone of Gazeau–Klauder coherentstate|s,ξ〉building is the energy spectrum of the system in question. Minimal parameterizations enabled Gazeau and Klauder to denote their coherent states by[32]
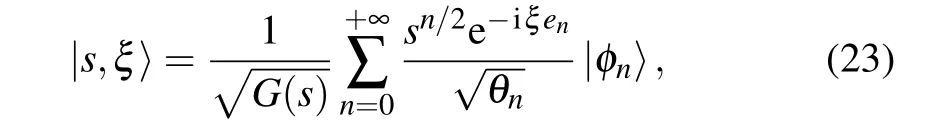
in whichsis the coherent state parameter constrained to belong to the disk{s ∈C,|s|<R}.Rdenotes the radius of convergence of the previous series,ξis the angular variable andθn=e1×e2×...×enwithenknown as the dimensionless energy of the system,expressed as
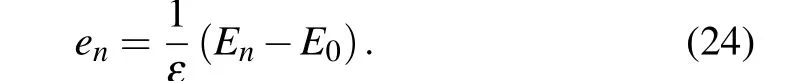
The parameterεwith the energy dimension is introduced to scaleen, rendering it dimensionless. Consequently, Eq. (24)together with Eq.(9)provide us with
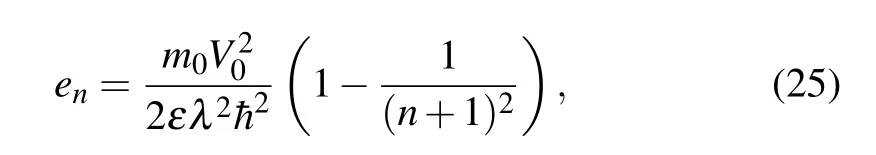
leading to the computation of the productθnof the dimensionless energies as

It is obvious that for the sake of simplicity, we have setaas the modified space deformation coefficient,say

On the other hand, the normalization factorG(s) will be obtained on the basis of the standard condition stated as〈s,ξ|s,ξ〉=1. It then follows from Eq.(23)that
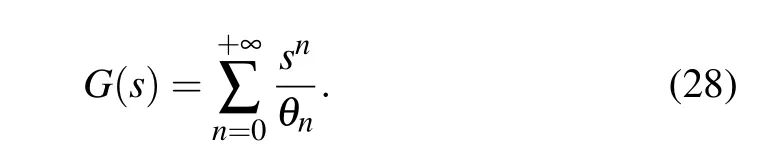
Elements from Eqs.(26)and(28)can be connected to generate an elegant form of this normalization factor in terms of a confluent hypergeometric function,say
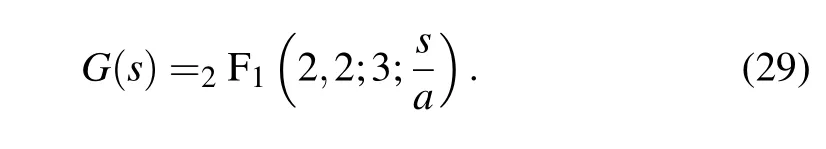
Substituting Eq. (26) into Eq. (23) yields the family of states we seek to study
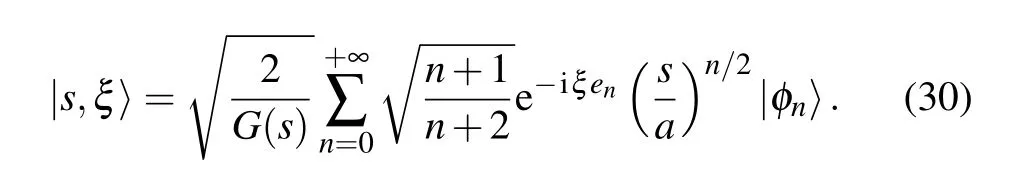
Stated otherwise, the expression given in Eq. (30) stands for the Gazeau–Klauder coherent states of our position-dependent mass system confined in the Coulomb-like potential given in Eq.(4).
3.2. Basic properties of Gazeau–Klauder coherent states
A suitable way to probe the existence of such a series solution is to compute the radius of convergenceR, as follows:[32]
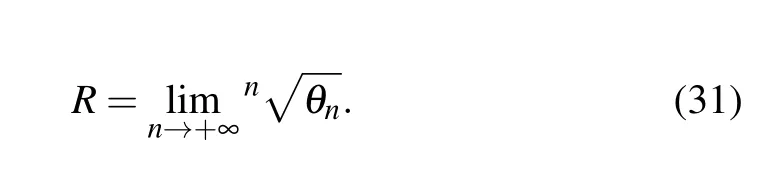
Using Eq.(26)in Eq.(31),a straightforward calculation shows thatR=a, which is an interesting feature. Thus, we can argue that Gazeau–Klauder coherent states for the position dependent-mass system under consideration do exist, but are not defined on the whole complex plane. This result is not surprising if one takes a closer look at the energy shape in Eq. (25). In agreement with Eq. (30) the scalar product between two representatives|s,ξ〉and|s',ξ'〉of the Gazeau–Klauder coherent-state family reads
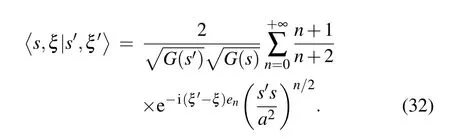
The latter real-valued expressions'scannot vanish. So,the previous overlap is a non-zero number. Consequently,the Gazeau–Klauder coherent states for the studied positiondependent mass system do not form an orthogonal family.The family{|s,ξ〉}is therefore said to be overcomplete. Apart from overcompleteness, the continuity property is another Klauder minimum requirement for a family of states to be termed coherent.[48]Here, continuity has a peculiar connotation, say, for a family mapping, such that|s,ξ〉→|s',ξ'〉,it follows that|||s,ξ〉−|s',ξ'〉||→0. Adapting the previous definition to our problem of a Coulomb-like potential induces the following norm:
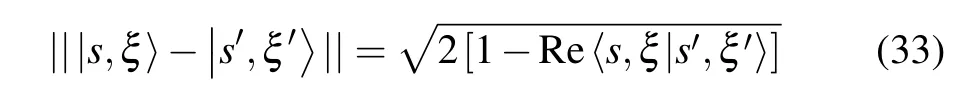
which tends to zero for|s,ξ〉approaching|s',ξ'〉. As a strong point of this result,we assert that the family of vectors{|s,ξ〉}forms a continuous and connected submanifold in the configuration space.
3.3. Statistical properties of Gazeau–Klauder coherent states
The statistical features of the Gazeau–Klauder coherent states for the studied position-dependent mass system can be investigated through the photon number distributionσn, defined as the squared modulus of the weighting coefficient of Eq.(30),that is,
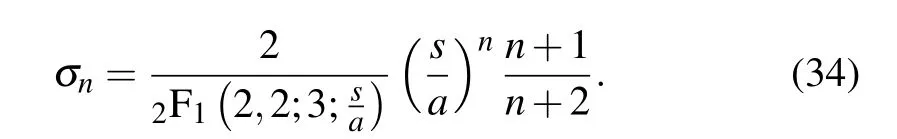
The mean excitation number is defined as the first moment of the photon number distribution,as
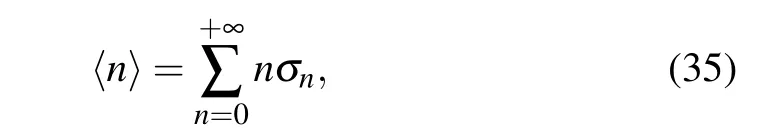
that has been computed and then expressed in terms of the confluent hypergeometric functions as

In a similar manner,the second moment of the photon number distribution reads

equivalent to
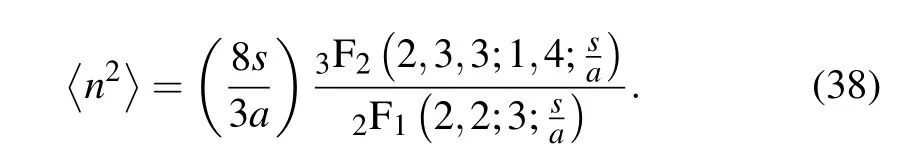
It is henceforth an easy task to derive the variance (∆n)2=〈n2〉−〈n〉2of the distribution from Eqs.(36)and(38)as

All the requisites contained in Eqs.(34), (36), and(38)stand for the basic elements required to gain insight into the statistical behavior of our system. For this purpose,we have started by plotting in Fig. 2 the photon number distributionσnas a function of the quantum numbernfor various values of the Gazeau–Klauder coherent-state parametersand the nonlinearity coefficienta. It can be seen that the distribution is a deformed Poissonian. This was to be expected,due to the fact that the system possesses a Coulomb spectrum. In addition,a simple observation of Fig. 2 shows that, for all values ofs,theσn-curve is narrower than the standard Poissonian. This points out the sub-Poissonian nature of our distribution.[3,8]Figure 3 shows that no matter how the nonlinearity coefficientachanges,the mean of the photon number distribution remains greater than its variance. This observation clearly indicates that the distribution is not Poissonian. Nervertheless,for small values of the coherent state parameter,the mean and the variance of the distribution evolve towards a point of coincidence.It appears in the previous figure that the mean〈n〉of the distribution and Gazeau–Klauder coherent-state parametersare two quantities that are proportional to each other. The Mandel parameterQis an interesting instrument for classification of the photon number distribution. In fact, the distribution is Poissonian forQ=0, super-Poissonian forQ >0 and sub-Poissonian ifQ <0.[49,50]This parameter is given by

Fig. 2. Plot of the photon number distribution σn versus the quantum number n for (i) s=0.010, (ii) s=0.011, (iii) s=0.012 and (iv) the standard Poissonian in the contexts of(a)a=0.019 and(b)a=0.025.
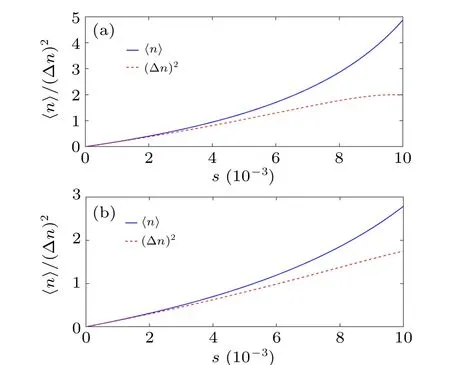
Fig. 3. Plot of the mean and the variance of the photon number distribution versus the coherent-state parameter s for (a) a=0.015 and(b)a=0.019.

plotted in Fig. 4(a). The latter figure shows thatQ <0 in the present case. Consequently, the Gazeau–Klauder coherent states for the position-dependent mass are subject to sub-Poissonian statistics. In other words, the expected value of the photon number is always larger than its fluctuations. The previous result can be strengthened by studying the last parameter,called the second-order correlation function,g2(0)given as
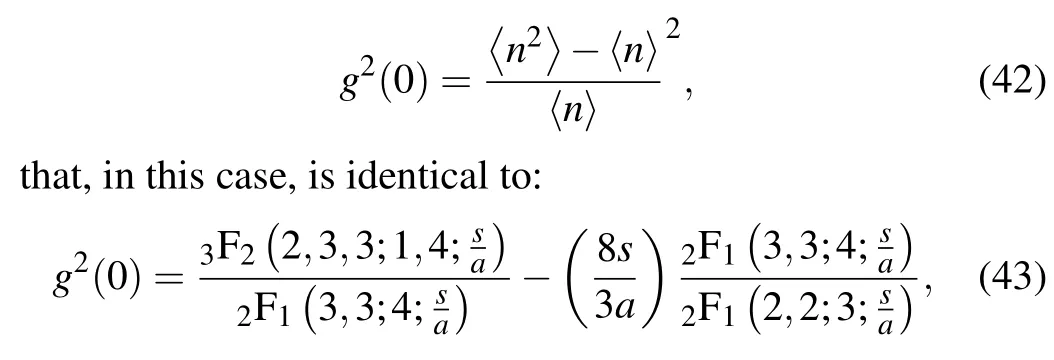
as plotted in Fig. 4(b). It is well known that a distribution is Poissonian forg2(0)=1,super-Poissonian forg2(0)>1 and sub-Poissonian ifg2(0)<1.[49–52]The case we are dealing with,g2(0)<1,evidently confirms the sub-Poissonian nature of the photon number distribution,no matter the change in the nonlinearity coefficienta.
We now conclude this section by noting that the Gazeau–Klauder coherent states for the position-dependent mass system trapped in a Coulomb-like potential exhibit an effect that has no analog in classical mechanics, the anti-bunching phenomenon.[53]
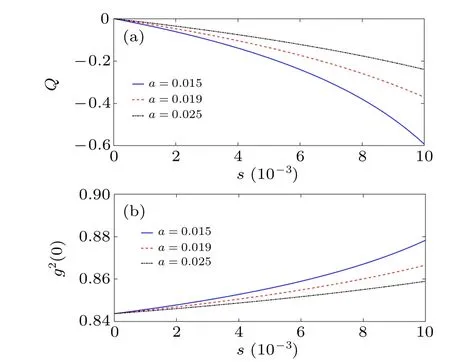
Fig.4. Plots of(a)the Mandel parameter and(b) the second-order correlation function versus s for various values of the modified nonlinearity coefficient a.
4. Temporal evolution of Gazeau–Klauder coherent states
4.1. Time scales in wave packets evolution
Quantum states are expected to show a recurrent behavior,consisting of a series of collapses alternating with revivals as the time passes.[54–56]The structure of these recurrences is strongly linked to the energy eigenvalues of the relevant system.It is well known that an individual eigenstate is stationary,and consequently exhibits no motion. On the contrary,a wave packet that is localized in a space admits variable expectation values as time evolves. One says that localized wave packets are dynamically nonstationary. It is worthwhile pointing out that the propagation of the previous wave packet is framed by the correspondence principle,which asserts that classical and quantum mechanics must agree in the context of highly excited states.Hereafter,we hold wave packet dynamics to be a strong tool for the study of our system’s time evolution. The motion of wave packets of energy valuesenlocalized around a central quantum numbern0is governed by the important timescales defined as
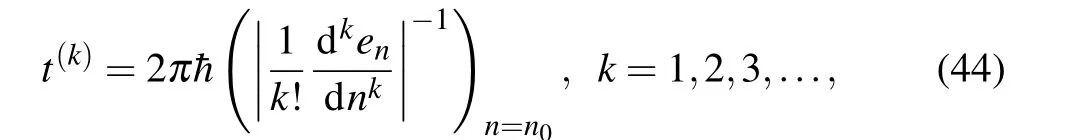
such thatt(k)<t(k+1). A proof of this inequality is provided in the Appendix. To obtaint(k), we write the energy in terms of the Taylor series with respect to the quantum numbernthrough a finite order. After this, we find times that cause the wave function’s phase to be a multiple of 2π. Here,t(1)is the classical period of the motion denoted bytc,t(2)stands for the revival timescale denoted bytrandt(3)is the super revival timescale,recorded astshereafter. In the special case of the harmonic oscillator the wave packet never fully collapses and there are no revivals.[57,58]Systems such as the rigid rotator, the infinite well, etc., that record an energy expression quadratic in the quantum number,undergo collapses and quantum revivals on a timescaletr.More realistic physical systems,such as Rydberg clusters are recognized to display more complicated revival patterns.[58,59]A study of the role of terms in the Taylor expansion of the energy is provided by Ref. [60],in which it is shown that at the timest ≈(n1/n2)tr, wheren1andn2are co-prime integers,the wave packet may be approximately rewritten as an equally weighted sum of subsidiary wave packets. These are the so called fractional revivals.
4.2. Quantum collapse and revival sequences
To apply the preceding ideas to the particular case of Gazeau–Klauder coherent states for the position dependent mass system, we should commence by using the timeevolution operator in Eq. (23) to write the time-dependent wave packets|s,ξ,t〉of the coherent states as
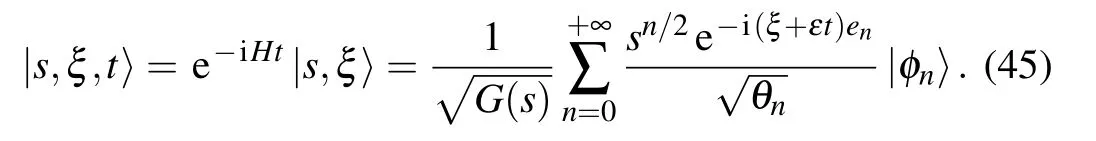
In the literature,a convenient way to probe some aspects of the Gazeau–Klauder coherent states during their time evolution is through a study of the autocorrelation functionC(s,a,t) defined as the scalar product between the initial coherent states given in Eq.(30)and the previously constructed time-evolved wave packets,
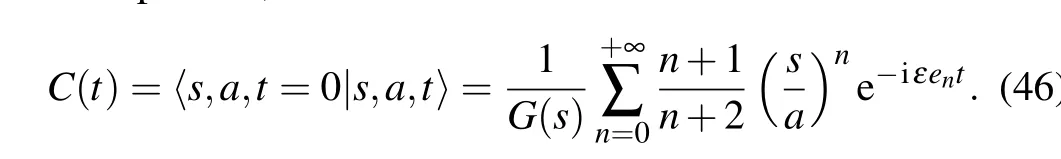
The idea here is attached to the constraint 0≤|C(t)|2≤1.More precisely,higher values of|C(t)|2,known as the survival function, occur when the wave packets reproduce their initial states. Conversely,low values of|C(t)|2correspond to the situation of waves that are far from their initial shapes.[58,61]We have substituted Eq.(25)into Eq.(44)and derived the following timescales:
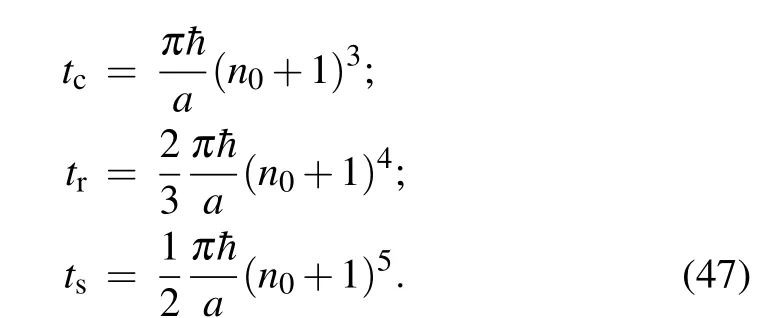
One straightforwardly notices from Eq.(47)that all timescales are proportional to the quantum numbern0of the most probable state,and consequently to the coherent-state parameters,keeping in mind the observations in Fig.3. Contrariwise,t(k)are scaled down by the space deformation coefficienta. In the context of highly excited particles, the system may experience the hierarchyt(k)≪t(k+1).[62]This is the case if one choosesn0=91 as the central quantum number. The various timescales are thus found to betc⋍0.0039,tr⋍0.2420 andts⋍16.6958 (in microseconds (µs)) fora=0.015. The motion of wave packets of Gazeau–Klauder coherent states propagating in the Coulomb-like potential is simulated using the survival function in Fig. 5. This figure provides us with rich information about the quantum system. One sees that the coherent-state wave packet initially oscillates with a period oft ≈tc. After a few classical oscillations, phase interference leads to the contraction of the wave packet, that is, the collapse phenomenon. The wave packet is revived after a timet ≈trand reconstructs its initial form; this is the quantum revival discernible in Fig. 5(b). This revival structure cannot be considered as an ideal one. In our mind, the reason for this is simple. The function given by Eq.(34)that typifies the Gazeau–Klauder coherent states being studied is not a normal Poissonian function compared to


Fig.5. Plot of the survival function versus time for s=0.01,a=0.015,and n0=91,in arbitrary units.

Fig. 6. Plot of the survival function versus time for (a) n0 = 5 and(b)n0=12,with s=0.01,a=0.015.
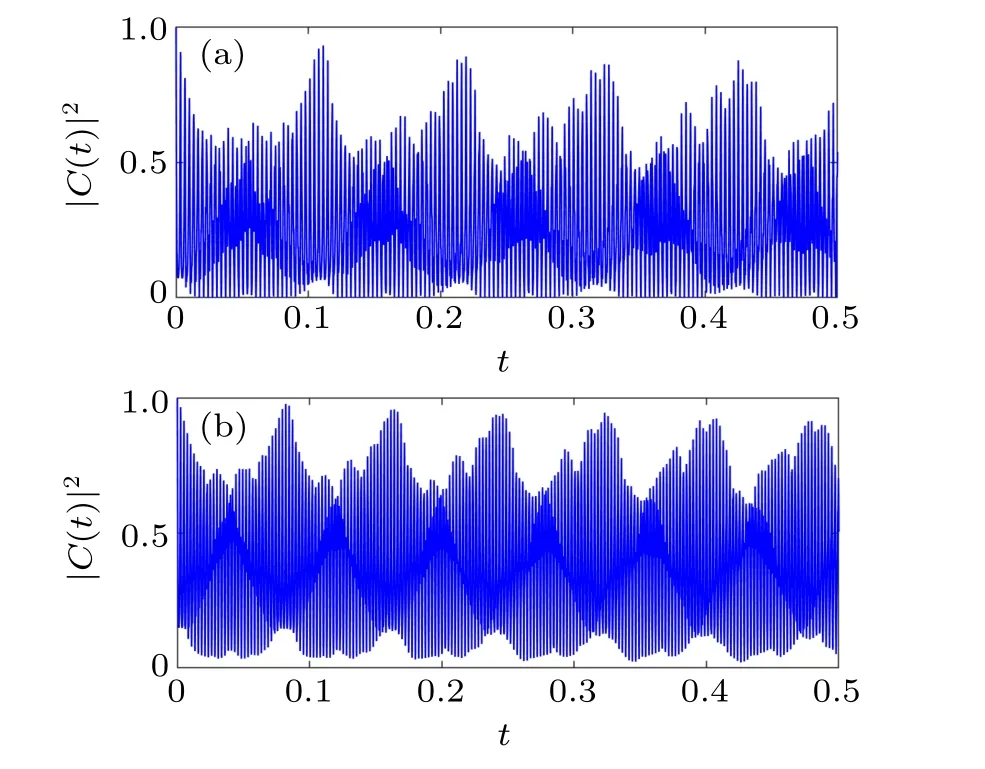
Fig. 7. Plot of the survival function versus time for(a) a=0.019 and(b)a=0.025,with s=0.01,n0=91.
It is obvious that the revival peaks are not as high as expected in Fig. 5. More precisely, as time evolves, they undergo a decay due to higher-order terms in the wave packet expansion that introduce a distortion into the quantum revivals.[62,63]From a closer look at the revival pattern,it emerges that there is a delay during the appearance of the simulated quantum revivals of the system, compared to the theoretical prediction. For example, the fractional and full revivals expected att ≈tr/2⋍0.1210 andt ≈tr⋍0.2420, respectively, actually appear later, at aroundt ⋍0.1410 andt ⋍0.2777, as displayed in Fig.5. We have studied the motion of wave packets in the context of low values of the central quantum number.It can be seen from Figs. 5 and 6 that regardless of the low or high value of the central quantum numbern0, the revival structure remains evident for a fixed value of the nonlinearity parameter. This observation is in contrast with the results of Naila Amiret al.in 2017, when they studied Gazeau–Klauder coherent states of an oscillator in a deformed quadratic potential.[27]On the other hand, an increase of the modified nonlinearity parameterainduces a decrease of the timescalest(k),and consequently an increase of the number of revival cycles for the same duration, as can be seen in Fig.7.We can now assert that strongly nonlinear systems exhibit more revivals than the others. In what follows,we investigate the behavior of wave packets when the simulation duration is sufficiently increased.
4.3. Long-term evolution of wave packets
We are now interested in the long-term evolution of wave packets for Gazeau–Klauder coherent states in a Coulomblike potential. The coherent states under consideration are expected to display interesting features at times up totsor fractions thereof. In Ref. [62] the reader can find a convincing mathematical explanation that may permit us to predict the revival regime of a quantum-mechanical system. On the other hand, this quantum revival structure can also be predicted by solving the following phase-difference equations:[61]

Fig.8. Plot of the survival function versus time for a=0.015,s=0.01,and n0=91 during the first 8µs.
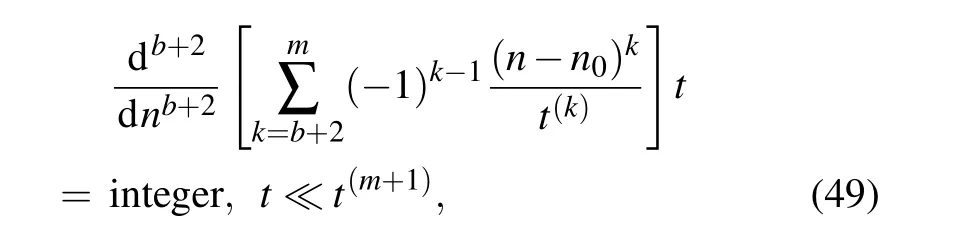
in which the timescalest(1),t(2),andt(3),respectively,representtc,trandts,whilet(4)stands for the timescale corresponding to the fourth-order term in the Taylor expansion of wave packets. Equation(49)gives some approximations for the revival pattern of systems that possess timescalest(k)obeying the hierarchyt(1)≪t(2)≪t(3)≪t(4). For orderb=0, this phase-difference equation produces information about quantum revivals with a timescaletr. The longer timescale,ts,known as the super-revival time,records the orderb=1. Thus Eq.(49)provides us with

yielding solutionst=ts/6,ts/3, etc., that exactly match those obtained in Ref. [62]. We have simulated the motion of wave packets for Gazeau–Klauder coherent states in the Coulomb-like potential during the first 8 µs, for which the central quantum numbern0=91 and the deformation coefficienta=0.015, corresponding to the super-revival timescalets⋍16.6958; the results obtained are displayed in Fig. 8.From this figure, it is easy to see that the full-revival peaks gradually decay in size as well as losing their periodicity. This collapse of wave packets evolves until aroundt ⋍3.4373 of Fig. 8(d), corresponding to a new sequence of revivals. This sequence later repeats neart ⋍6.3190, as seen in Fig. 8(g),with a peak higher than that of the first revival;this is a super revival.These fractional super revivals were expected to occur att ≈ts/6⋍2.7826 andt ≈ts/3⋍5.5652,respectively,rather than att ⋍3.4373 andt ⋍6.3190.This delay can be explained by the loss of periodicity previously mentioned, certainly introduced by the deformation in the coordinate space manifest in the variable changes of Eq.(5). The height of the survival function’s peak provides evidence that the super revival looks more like the initial wave packet than the revival packet does,whent ≈tr.
5. Conclusion
This communication focused on Gazeau and Klaudertype coherent states of a mechanical system with a spatially variable mass confined in a potential similar to that of the 1D Coulomb problem. The ensuing energy spectrum appeared in the expected form with an inverse quadratic dependence onn. We found that these energy levels are tightened in strongly nonlinear systems. Using the probability distribution of the photon number revealed that the underlying system exhibits an antibunching phenomenon. Moreover, the temporal evolution of this mechanical system was explored by using the survival function. It was made clear that the wave packets of Gazeau–Klauder coherent states undergo quantum revival and super-revival cycles with a progressive loss in periodicity,consequently leading to their evanescence.
We believe that our work sets the stage for a conceptual and practical understanding of wave packet propagation in systems with position-dependent effective masses in the presence of Coulomb-type confinement potentials.Such systems can be exemplified by bottom-up fabricated atomically-precise segmented graphene nanoribbons, SGNRs. One aspect of this conceptual understanding emanates from both Eqs. (27) and(47),where it is evident that the revival times are proportional toλ2, a manifestation of time dilation brought about by the non-singular nature of the Coulomb-type potential studied.
Appendix A
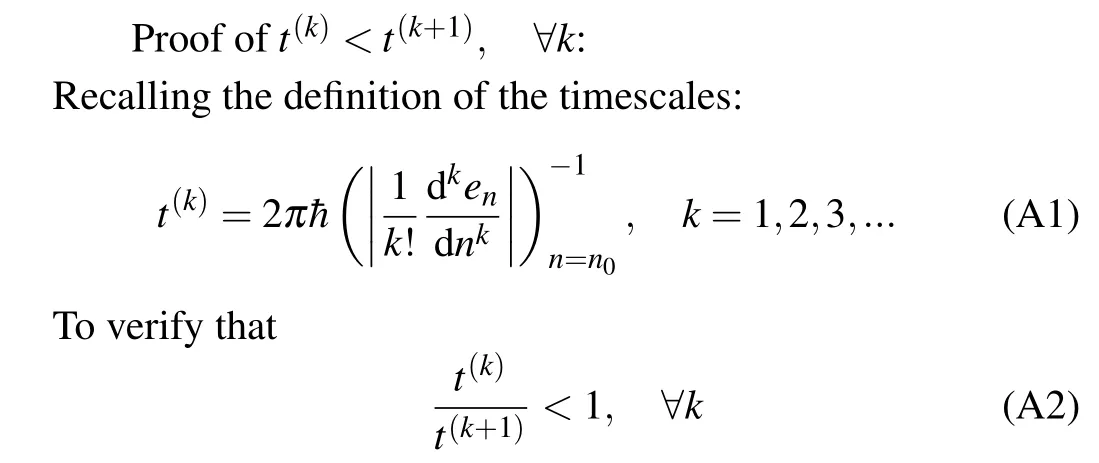

杂志排行
Chinese Physics B的其它文章
- Quantum computation and simulation with vibrational modes of trapped ions
- ℋ∞state estimation for Markov jump neural networks with transition probabilities subject to the persistent dwell-time switching rule∗
- Effect of symmetrical frequency chirp on pair production∗
- Entanglement properties of GHZ and W superposition state and its decayed states∗
- Lie transformation on shortcut to adiabaticity in parametric driving quantum systems∗
- Controlled quantum teleportation of an unknown single-qutrit state in noisy channels with memory∗
