板式直线压电振子的拓扑优化与实验∗

朱 华，崔云鹏，牛瑞坤

（南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016）

引言

目前，对于超声电机的结构设计比较常见的方式是采用尺寸优化确定电机定子的几何参数，使用此种方法进行电机结构设计比较简便，但是在特定的尺寸范围内，对于电机性能的提升具有局限性［1‐4］。

近年来，许多学者尝试了不同的方法来设计超声波电动机的结构［5‐7］。Gilder 等［8］等对一种压电柔性换能器进行了拓扑优化设计。万志坚［9］通过在矩形板上打4 个槽用于减小谐振的频率差，仿真后发现这种方式同样可以增加驱动足的振幅。唐茜［10］通过拓扑优化技术对杆状超声电机的定子结构进行设计，通过放大驱动足的振幅提高电机的性能。M'Boungui等［11］以输出点位移响应最大为目标，利用拓扑优化的方法设计了一款利用2 个谐振频率比为1∶2 的贴片式直线超声波电动机，其空载速度为14 mm/s，最大推力为50 mN。张百亮等［12］提出将V型直线电机前端盖开圆弧形槽增加驱动足处振幅，通过实验得出开槽后的电机性能有了一定的提升。

笔者提出通过对矩形板式的直线超声电机定子结构进行拓扑优化设计，旨在不改变电机几何外形尺寸的条件下提高板式直线超声电机的机械性能。对优化前后的电机进行实验分析后发现，电机定子结构的拓扑优化设计可以在一定程度上提高电机的性能。

1 电机结构和拓扑优化方法

1.1 电机结构

电机整体结构如图1 所示，由动子导轨、矩形板电机和预压力调节器组成。超声波电机的定子结构由矩形金属板和8 片压电陶瓷组成，压电陶瓷片用环氧树脂胶均匀地附着在金属板的正面和背面，其中定子选取的金属基体为磷青铜（Qsn），压电陶瓷片为PZT‐8。这种类型的电机利用压电陶瓷的d31效应，主要用于具有线性输出的微型超声波电动机。

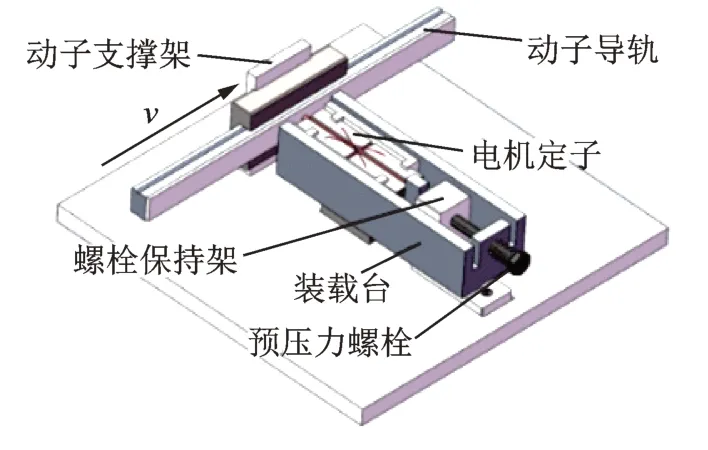
图1 直线电机整体结构Fig.1 The overall structure of the linear motor

1.2 电机工作原理

对于这种类型的超声电机，矩形板的平面内1阶纵向伸缩振动和平面内2 阶弯曲振动模式通常用于工作中，两种模式可以以相同的频率彼此耦合，从而使定子能在驱动足处形成椭圆运动。加电方式为在对角线方向上分别施加正弦和余弦电压，如图2 所示。定子用于工作的两种振动模式如图3所示。

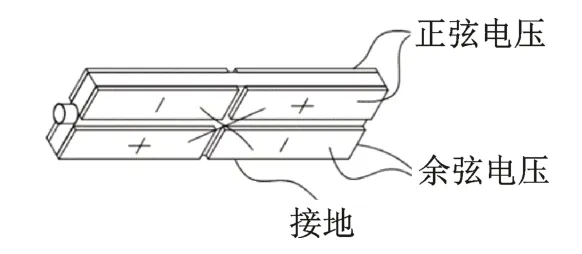
图2 压电陶瓷极化方式Fig.2 Piezoelectric ceramic polarization

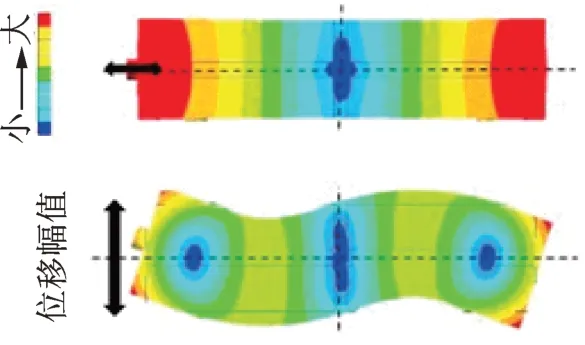
图3 定子振动模态Fig.3 Stator vibration mode

1.3 拓扑优化方法

目前，变密度法（solid isotropic microstructures with penali‐zation，简称SIMP）主要用于连续体的拓扑优化［13‐15］。SIMP 法是将设计区域的材料密度设置为0～1，设计变量为材料的密度值大小，0 表示材料去除，1 表示材料保留［16］。为了更好地激发电机的工作模态，拓扑优化过程中采用三平面对称的约束条件，使3 个对称面均通过矩形板的中心位置。对矩形薄板粘贴压电陶瓷位置处施加与压电耦合效应等效的简谐激振力，为之后进行拓扑优化分析进行前处理工作。图4 为力加载仿真示意图，其中矩形板的绿色部分为施加正弦电压时等效激振力所激励的区域，红色部分为施加余弦电压时等效激振力所激励的区域。

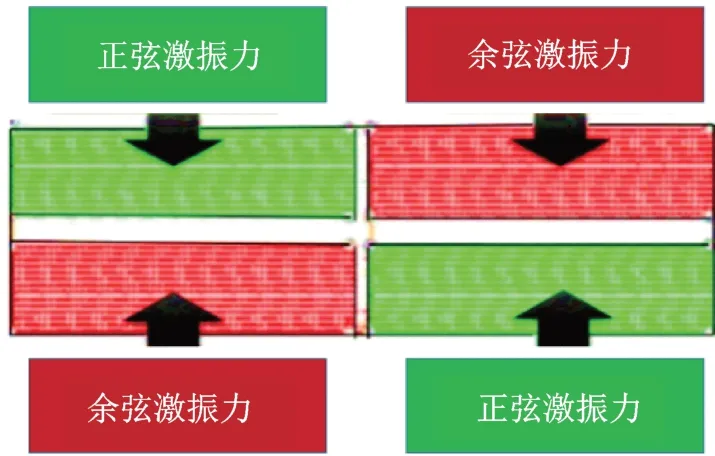
图4 激振力加载矩形板表面Fig.4 Exciting force loading rectangular plate surface

2 定子结构设计

超声电机的工作性能好坏与定子结构的设计相关，笔者采用对电机定子部分进行拓扑优化设计，在不改变电机几何形状的情况下，进一步提高电机的输出性能。

2.1 结构优化设计

通过对现有的文献调查研究可知，驱动足振幅与定子结构力系数相关，通常是在一定的范围内，驱动脚振幅越大，电机的性能就越好［17］。在等效激振力作用下，首先以增大定子驱动足的横向振幅为目标，对定子进行拓扑优化分析，得到的结果如图5 所示。其中结构的红色与蓝色部分表示其单元密度值由大到小分布，从图中可以看出，去除矩形板中间位置两侧一部分的材料，会使驱动足处的振幅有一定程度的增加。超声电机输出效果与施加的预压力有关，预压力大小直接影响电机的运动特性。动子摩擦层与驱动足之间的接触距离又会对两者之间的压力产生影响［18］，即预压力施加的大小与定子预压力施加方向的振幅有关。在一定激励频率范围内，椭圆运动的纵向振幅大小决定输出驱动力的大小，横向振幅大小决定输出速度的大小。但过于增大纵向振幅，会降低定子的纵向局部刚度，不利于超声电机的工作，因此笔者在对定子进行设计时，尽量使纵向振幅保持不变，而增大横向振幅，以此减小拓扑优化后对定子纵向刚度的影响。图6 为纵向刚度的拓扑优化结果。为了更清楚地表示目标函数与设计变量的关系，拓扑优化数学模型为

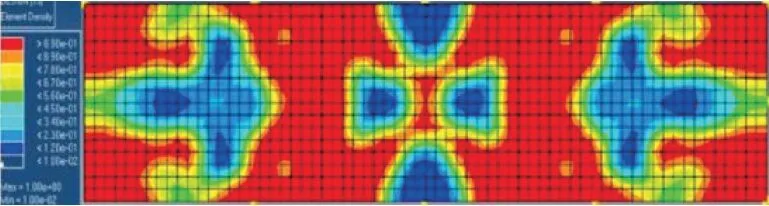
图5 定子横向振幅拓扑优化结果Fig.5 Stator lateral amplitude topology optimization results

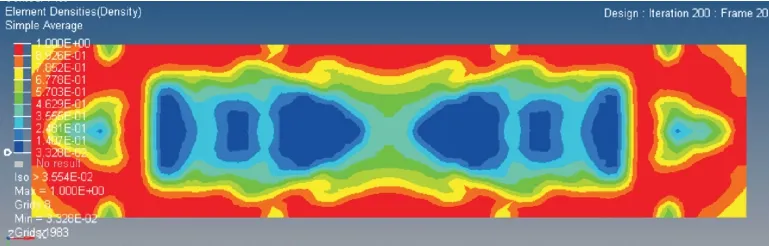
图6 定子纵向刚度拓扑优化结果Fig.6 Topological optimization results of stator longitudinal stiffness

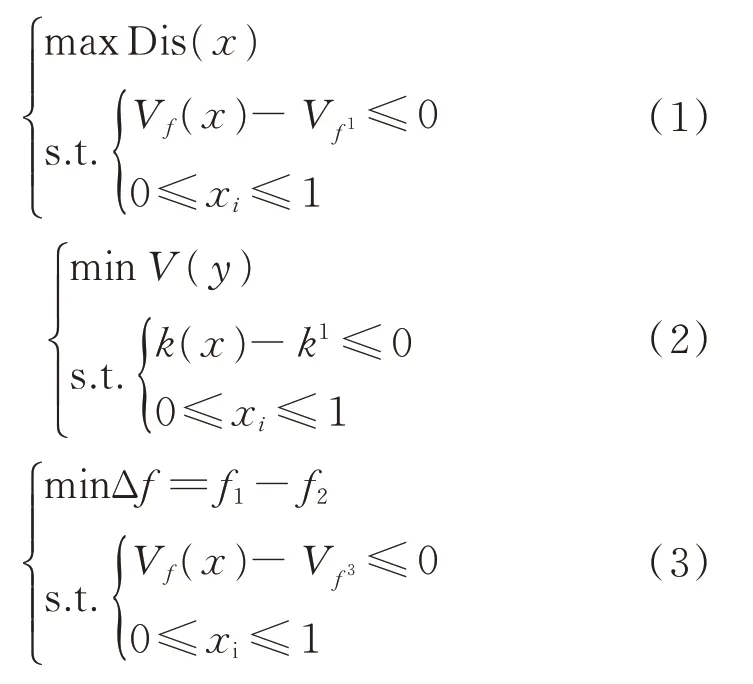
其中：函数Dis（x）为定子结构的横向位移响应；V（y）为结构的总体积；k1为结构的刚度要求；Δf为定子两种工作模态所对应频率的差值；为结构的体积分数要求；设计变量xi为单元密度值。

以上的分析均是对定子力学方面的拓扑优化分析所得到的结果。另外，此类直线超声电机工作的主要方式是利用2 阶弯曲振动模式和1 阶纵向振动频率相互耦合，因此围绕优化电机工作模式的频率一致性，以提高电机的输出性能。优化设计方案如表1 所示。定子结构频率优化结果如图7 所示，迭代曲线如图8 所示。

表1 优化参数Tab.1 Optimization parameters

图7 频率拓扑优化结果Fig.7 Frequency topology optimization results

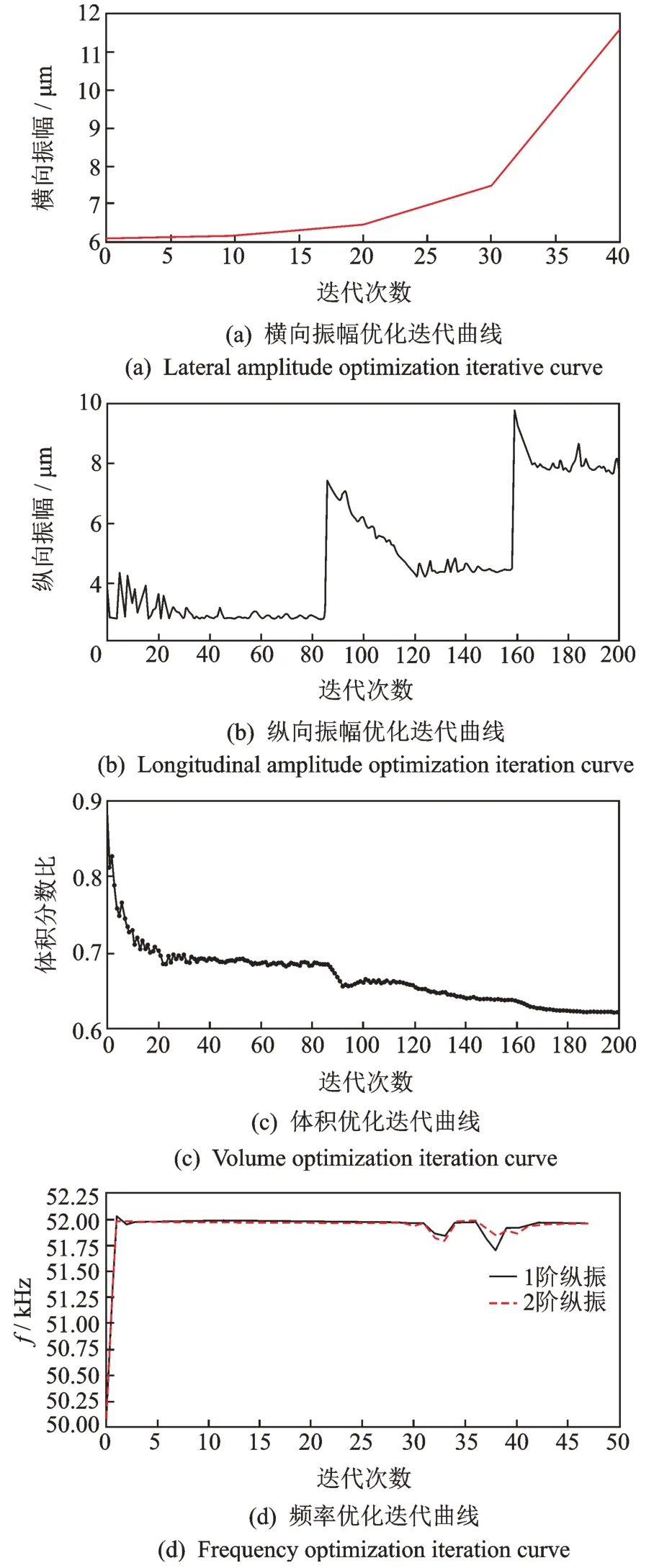
图8 迭代曲线图Fig.8 Iteration graph

从以上分析结果可以得出，去除定子4 个顶角部分和定子2 阶弯振节点处的材料，能够减小1 阶纵振和2 阶弯振的频率差。由图6 纵向刚度优化结果可知，去除2 阶弯振节点处的材料，对电机纵向刚度影响较小。施加等效激振力后，以增大定子顶部横向振幅为目标进行拓扑优化设计，从结果可知，在2 阶弯振节点处去除材料会增加驱动足的横向振幅。通过对上述拓扑优化结果的综合分析，设计出拓扑优化后的定子结构。考虑到孔的数量会对结构的局部刚度和强度有很大的影响，孔的数量不应过多，而且定子设计成对称式结构能更有效地激发所需模态。综合以上分析，定子的几何结构设计如图9 所示。

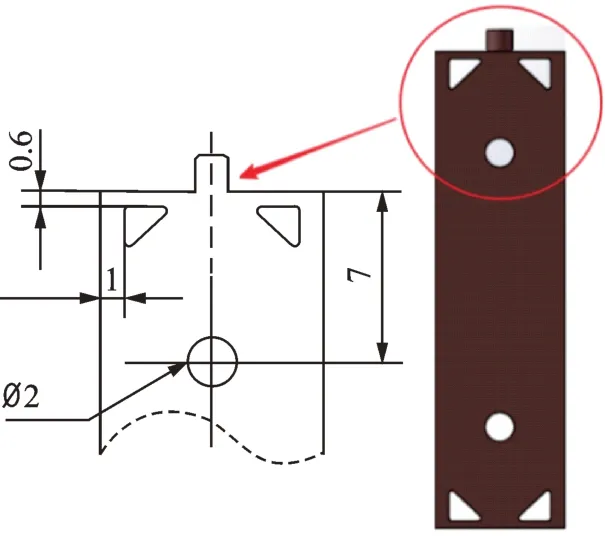
图9 优化后定子结构图(单位：mm)Fig.9 Optimized stator structure (unit:mm)

2.2 仿真分析

使用ANSYS 有限元仿真软件对原型电机和拓扑后的电机进行谐响应分析，这里将原型电机设为Ⅰ号机，拓扑优化后电机设为Ⅱ号机。Ⅰ号机和Ⅱ号机谐响应分析曲线分别如图10 所示。通过仿真结果可以得出，拓扑优化后的电机频率一致性较优化前的要好，驱动足处的振幅也有一定的提升，其中横向振幅提升较为明显。为了更直观地表达振幅的变化，绘制了驱动足仿真椭圆轨迹如图11 所示。从椭圆轨迹可以看出，优化定子结构后的椭圆轨迹大于优化前的横向振幅，满足上述的设计要求。

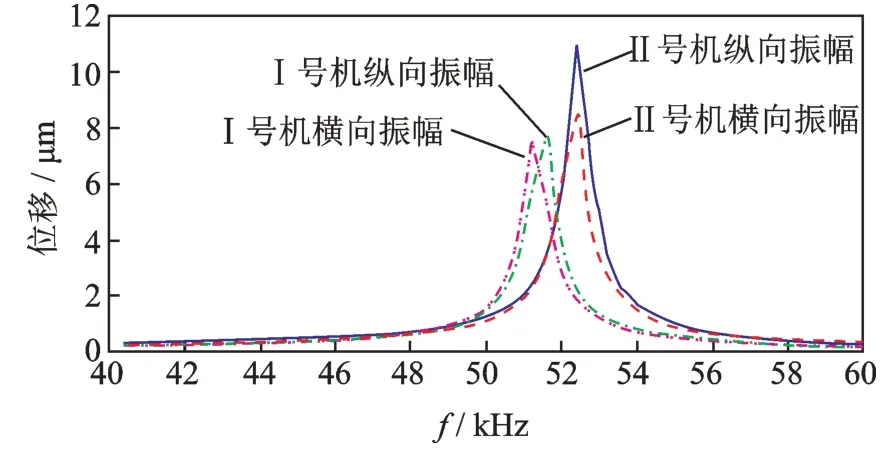
图10 谐响应分析仿真曲线Fig.10 Harmonic response analysis simulation curve

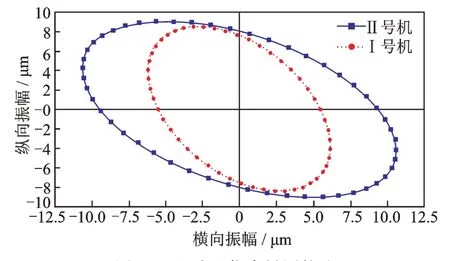
图11 驱动足仿真椭圆轨迹Fig.11 Driving foot simulation elliptical trajectory

3 实验与分析

通过前面仿真分析，加工制作出Ⅰ号电机和Ⅱ号电机，电机实物如图12 所示。其中线性导轨的一侧粘贴摩擦片（刚玉陶瓷），调节预压力螺栓压缩弹簧使其产生变形，进而对电机施加工作时所需的预压力。采用在导轨一端吊砝码的方式，测试电机推力大小。实验流程和设备如图13 所示，实验装置如图14 所示。

图12 电机实物Fig.12 The actual motor

图13 电机推力测试装置图Fig.13 Motor thrust test device diagram

图14 三维激光测振实验Fig.14 3D laser vibration test

使用三维测振分析后得到Ⅰ号机和Ⅱ号机振动速度频率响应特性曲线和定子测振振型如图15 所示。通过对定子结构进行扫频实验，选择驱动足处作为测试区，当对电机施加单相峰峰值为100 V 的激励电压时，从定子的频响特性曲线可知，Ⅰ号机的1 阶纵振和2 阶弯振模态分别对应53.752 和54.537 kHz 的实际激励频率，Ⅱ号机的1 阶纵振模态和2 阶弯振模态分别对应的实际激励频率为55.106 和55.259 kHz。Ⅰ号机和Ⅱ号机仿真和实验结果如表2 所示。从实验结果可以看出，电机的实际工作情况与有限元仿真分析结果大体相同，Ⅰ号机与Ⅱ号机相比频率一致性较差，但Ⅰ号电机工作时频率调节范围比优化后电机更大。

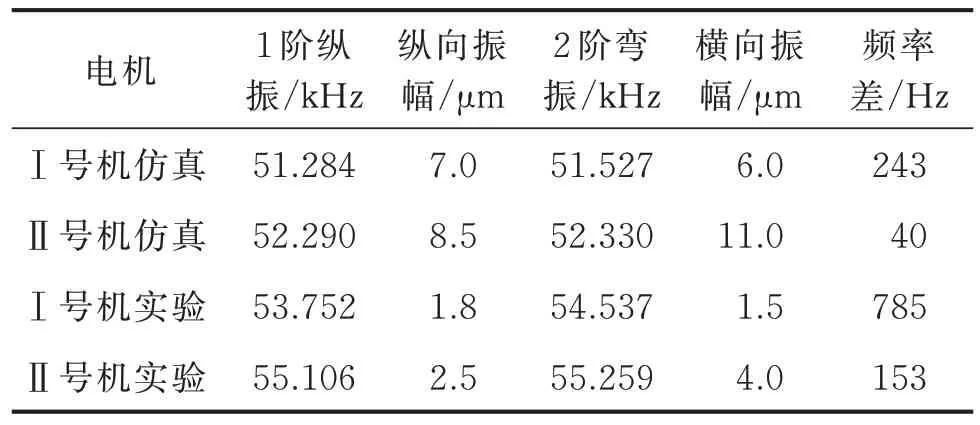
表2 定子拓扑优化前后数据结果对比Tab.2 Comparison of data results before and after stator topology optimization

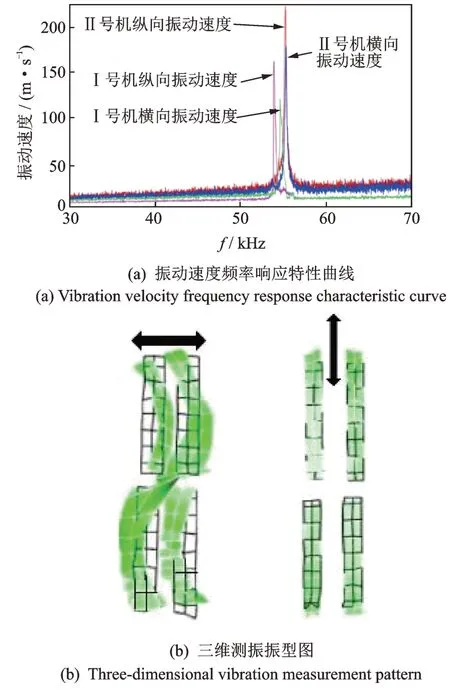
图15 三维测振实验结果Fig.15 Three-dimensional vibration test results

对Ⅰ号机和Ⅱ号机机械性能进行测试。空载速度和频率的关系如图16 所示，实验结果表明，Ⅰ号机和Ⅱ号机的最大空载速度分别为410 和460 mm/s，对应激励频率分别为54.12 和55.18 kHz。从实验数据分析可以得知，通过对电机定子结构进行拓扑优化设计后，可以一定程度上提高电机的空载速度。图17 为两种电机分别在其各自最佳激励频率、预压力分别为7 和10 N 时，激励电压幅值为400 V 时的速度与负载关系曲线。从图中可以得知，随着负载的增加，动子的速度越来越小，拓扑型电机的输出力提高了40%，推重比为38，而原型电机的推重比为23。

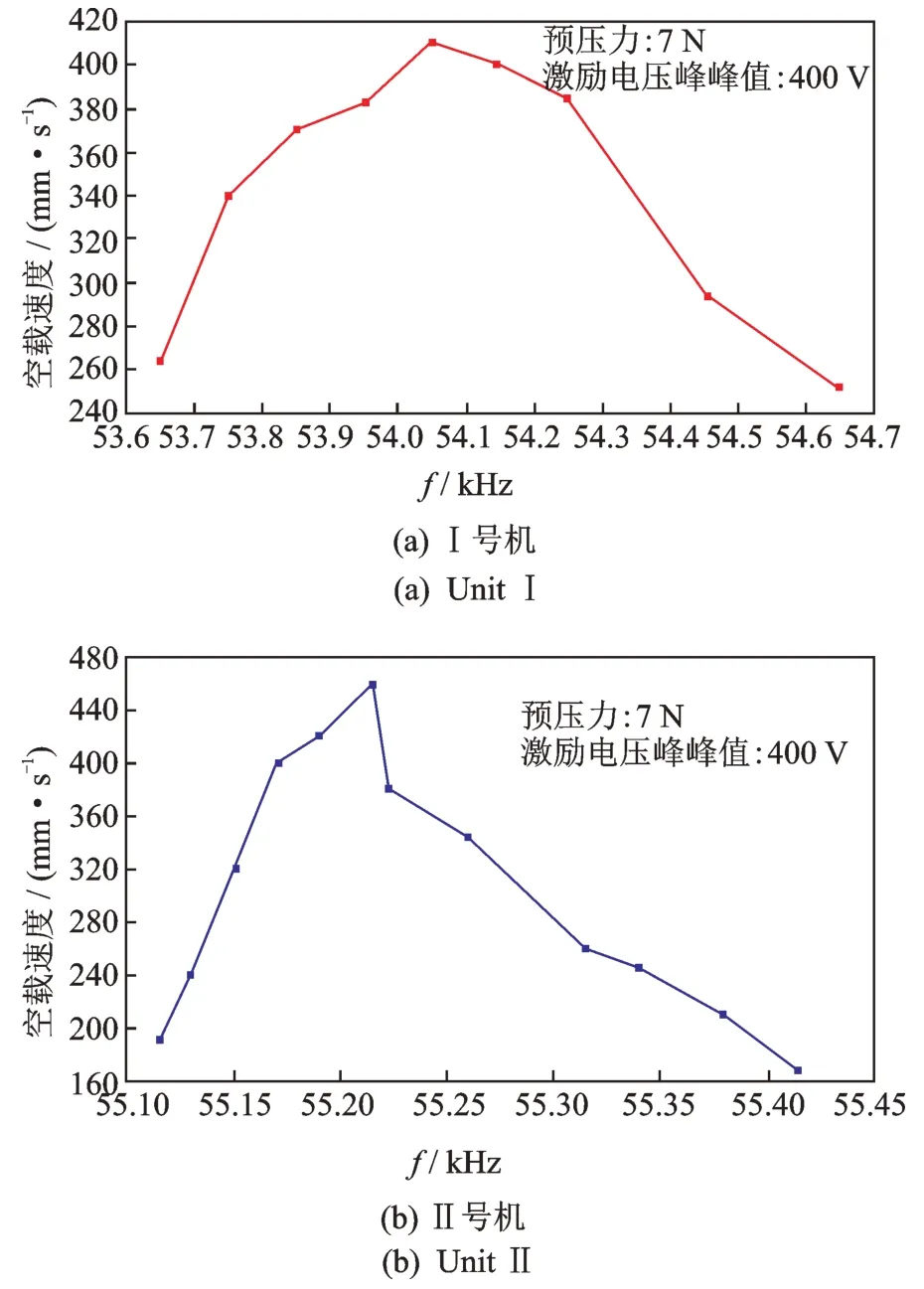
图16 电机空载速度频率曲线Fig.16 Motor no-load speed frequency curve

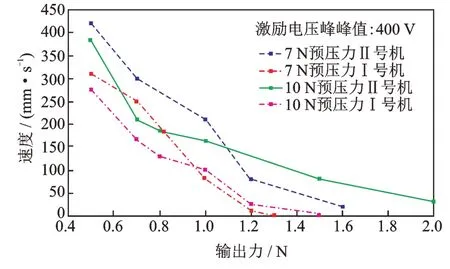
图17 不同预压力下负载与速度关系曲线Fig.17 Load and speed curve under different preloads

4 结论

1）笔者基于拓扑优化方法设计板式直线超声电机的定子结构，在不改变电机几何外形尺寸的条件下，提高了板式直线超声电机的性能。

2）通过有限元仿真分析得出，将电机的定子进行拓扑优化分析后，驱动足的振幅相对于原型机定子的驱动足有较大的提升。使用三维测振仪对电机的振动结果进行测试，然后对原型机和拓扑优化后的电机进行机械性能实验，证明了对超声电机定子进行拓扑优化设计后，电机的输出性能有明显的提升。

3）原型机和拓扑优化后的电机对应的最大空载速度分别为410 和460 mm/s，最大输出力分别为1.5 和2 N。相较于以往直线超声电机定子结构的设计方法，使用拓扑优化技术对定子结构进行设计后能够使电机获得更大的输出性能。