基于仿生学的微通道耦合射流系统设计与研究*

葛佳伟，徐伟杰，江 雄，金大元，景莘慧

（1.中国电子科技集团公司第三十六研究所，浙江 嘉兴314033；2.东南大学机械工程学院，江苏南京211189）

引 言

信息处理技术的微型化、高集成度、高功耗的发展趋势，使得电子设备的热流密度越来越高。局部温度过高已成为电子设备性能下降甚至失效的主要原因[1]。与常规风冷散热相比，微通道冷却和射流冷却作为新型高效冷却技术，具有更强大的换热能力，因而得到了广泛的关注和研究[2–3]。然而常规的微通道冷却系统压降过大，且沿着流动方向的均温性能不好。单纯的射流冷却技术作用范围小，阵列式分布又会使相邻射流之间产生干扰，造成交汇区域的换热系数急剧下降。微通道耦合射流冷却技术由于整合了微通道热沉冷却技术和射流冷却技术的优点,具有降温效果明显、均温效果好、压降小等优点[4]，被认为是未来解决高热流密度电子元器件散热问题的有效途径之一。

师法自然，自然界为人类提供了许多解决方案。每种生物经过数亿万年进化筛选出来的生物特征赋予其对环境非同凡响的适应能力，同时也为人类的技术进步注入了新的活力，如蜻蜓之于直升机，蝙蝠之于雷达，海豚之于声纳等。文献[5]受哺乳动物循环和呼吸系统分形模式的启发，设计了用于电子芯片冷却的分形分支微通道热沉。结果表明，分形分支通道网络比传统的并行网络具有更强的传热能力。文献[6]提出了一种新型微通道耦合射流冲击冷却方案，用于电子设备的高热流密度热管理，并用数值模拟对该散热器的均温性进行了优化。文献[7]在几种典型树叶形状的基础上，设计了树形微通道热沉的模型。结果表明，树形微通道具有更好的均温性,系统降压和被冷却的芯片温度更低。文献[8]对冲击射流作用下微通道散热器的强化传热进行了研究，通过试验对比，冲击空气射流作用下的微通道热沉的热阻比平行流作用下的微通道热沉的热阻提高了约48.5%。

本文借助自然界中典型的管网结构设计了3种仿生微通道耦合射流系统，并通过仿真计算研究了系统模型的流阻特性和换热特性，最后将研究成果应用于高热耗的贯通式液冷VPX模块，并通过实验验证了系统的散热性能。

1 微通道耦合射流模型

1.1 典型肋柱模型

典型肋柱模型为常用阵列式分布的柱形散热器，用于仿生模型的对比和分析。该模型采用边长为0.8 mm的正方形立柱，高度为4 mm，间距为0.8 mm。射流口位于模型的正上方，冲击后再向四周发散，如图1所示。

图1 典型肋柱模型与分形脉络模型

1.2 分形脉络模型

叶片脉络的主要特征为具有明显的主脉，再经过逐级分枝，细分为交错分布的细脉。叶片脉络描述了动植物必需的营养物质是如何在自相似的分形空间网络中输运的，经亿万年演化后将能量耗散率最小化。这种高效养分输运系统必然在物质输运及能量传递方面具有独特的优势。

分形脉络微通道耦合射流模型以荷叶为雏形，相较于传统流道，该模型采取中心射流、再向四周脉络流道扩散的形式，如图1所示。

该分形脉络模型具有多级脉络分叉结构，共有20条脉络，3种分叉等级。上下级流道的长度和宽度由Kleiber定律中的异速生长率决定[9]，即生物的生长速率或新陈代谢率B与个体质量M的3/4次方成正比，如式（1）所示：

该仿生模型上下级流道的深度、长度和宽度见表1。

1.3 斐波那契螺旋模型

斐波那契螺旋又称黄金分割螺旋，随着项数的增加，前一项和后一项的比值会无限逼近0.618。这是自然界中比较常见的一种结构，如海中的鹦鹉螺、银河中的星云、向日葵的种子等。生物的外壳及植物的种子在生长排布的过程中都希望最高效地利用好有限的空间，使其不至于太稀或太密，各部分都能得到比较均衡的营养与光照。

斐波那契螺旋耦合射流模型正是受此启迪而设计的，前后螺旋半径以逐渐逼近黄金比例的形式分布，以最有效地利用换热空间。该模型采用中心射流，然后向四周拓扑出20条流道。每一条流道按1/4圆弧内切生长而成，其半径按1 mm，1 mm，2 mm，3 mm，5 mm，8 mm，13 mm和21 mm以斐波那契数列规律增长，如图2所示。

图2 斐波那契螺旋模型与六方晶系模型

1.4 六方晶系模型

雪花多为六角形，是由空气中的水汽凝华而成的枝状或星状六方晶系结构。在雪花增长过程中，冰晶会消耗周围的水汽而形成短暂的局部负压，周围的水汽会根据负压分布选择一条最优路径补充过来。水汽在输运过程中凝华形成雪花的枝叉，如图2所示。

六方晶系模型以雪花为雏形，流道采用中间射流、再向四周拓扑的形式。该模型中心为一个边长为6 mm的正六边形，每个棱角上分出一条支路，每条支路两侧再分叉出宽度为0.6 mm的支路，如图2所示。

2 仿真分析

2.1 计算模型和边界条件

模拟流体流动时，湍流模型采用Realizablek-ε模型[10]，介质为连续介质，遵循连续方程、Navier-Stokes动量方程和能量守恒方程。微通道中的流动被认定为不可压缩的连续定常流，其控制方程见式（2）—（4）。

连续控制方程：

动量控制方程：

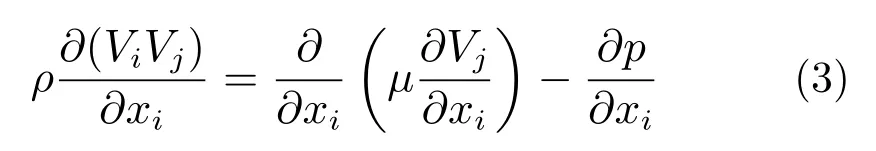
能量控制方程：

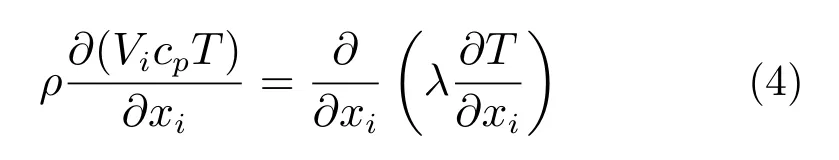
式中：Vi为水平方向的速度；Vj为垂直方向的速度；xi为位移；µ为动力粘度；p为压力；ρ为密度；cp为比热容；T为温度；λ为流体的传热系数。

模型材质为Al6061，导热系数为180 W/（m·K）；模型的进口采用质量流量进口，温度为55◦C，出口为压力出口，基准压力为标准大气压；流动域与固体域之间设置为耦合界面，其余界面采用绝热界面；模型底面设置热耗为40 W的热源，其尺寸为40 mm×40 mm；接触热阻为8×10−4m2·◦C/W。

为避免因网格质量引起的仿真结果误差，对网格独立性进行了分析。以分形脉络模型为例，采用5种不同的网格节点数量进行了模拟计算，结果见表2。

表2 网格独立性

从表2可以看出，随着网格节点数量的增加，前后芯片温升的最大偏差在0.5%以内。这意味着模型的网格是独立的，增加或较少网格对结果的影响较小。综合考虑计算精度和时间，最终确定网格数量为535 154个。

2.2 温度分布

当进口流量为0.6 L/min时，4种模型的温度分布如图3和图4所示。从图3可以看出，典型肋柱模型的冷却介质通过喷嘴射流至中央后，并没有均匀地向四周发散，而是主要顺着上下左右4个方向呈十字状向外发散，最后通过汇流槽汇流至出口。典型肋柱模型的中央区域为冲击区，温度最低，4个倒角处尤其是远离出口的2个倒角附近，由于流量相对较小，温度最高。

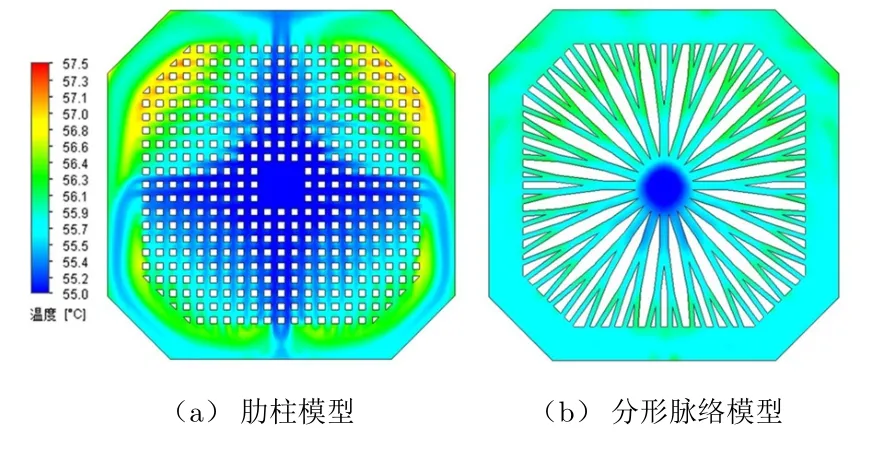
图3 典型肋柱与分形脉络模型温度云图

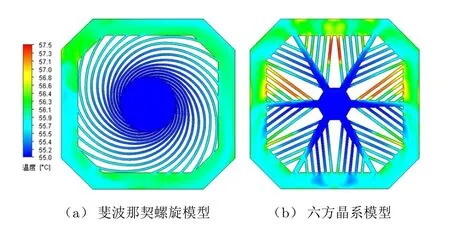
图4 斐波那契螺旋模型与六方晶系模型温度云图

分形脉络模型的冷却介质通过射流口喷射至中央并向四周拓扑，最后通过汇流槽汇流至出口。从温度云图可以看到，除了冲击区的温度相对较低，其余位置的温度梯度很小。

从图4可以看出，斐波那契螺旋模型中央的温度最低，各个螺旋线的温度分布基本相同。但汇流槽的左右流动情况并不对称，在以进口为圆心、与出口角度约为0.618π处开始分离，一部分冷却介质顺着螺旋线方向流至出口，而另一部分则逆着螺旋线方向流至出口。

六方晶系模型中央冲击区的温度最低，六条主要分支温度稍有不同，最长的旁路分支的流量较小，因而温度最高。

表3给出了4种模型芯片的最高温度、最低温度及其差值。通过对比可以看到：在流量一致的情况下，斐波那契螺旋和分形脉络的芯片温升和温差最小，平均温升分别为4.2◦C和4.4◦C；典型肋柱模型的换热特性相对较差，平均温升在4.9◦C，最大温差为1.2◦C。

表3 处理芯片最大温差与均值 ◦C

经综合分析，这4种微通道耦合射流系统的散热性能都很好，40 W处理芯片的平均温度都在60◦C以下，完全满足处理芯片的工作温度要求，证明微通道耦合射流系统具有强大的换热能力。

2.3 换热性能分析

平均努赛尔数Nu是表征固体对流换热量与流体内部传导换热量比值的无量纲参数，值越大说明对流换热越强烈，其计算公式为：

式中：D为入口处的当量直径；h为换热系数，本文为芯片热流密度与冷却介质定性温度和底面温度平均差值的比值。

雷诺数Re是惯性力和粘性力比值的无量纲参数，表征流体的流动情况，其计算公式为：

式中：U为流体入口处的速度；υ为动力粘度。

平均Nu随进口Re的变化如图5所示。

图5 平均努塞尔数与雷诺数的关系

从图5可以看出，4种模型的平均Nu随Re的升高而升高，增幅逐渐减小，说明一直提高流速对芯片散热的影响会逐渐减小。当Re>20×104时，3种仿生模型的平均Nu差距变小，与典型肋柱模型的差距逐渐拉开，表明仿生模型在高雷诺数区域也有很好的换热效果。在Re<20×104的区间，斐波那契螺旋模型的平均Nu最高，芯片温升最小，平均换热效果最好；其次是分形脉络模型和六方晶系模型；典型肋柱模型的Nu最低，芯片温升最高。

当进口流量为0.6 L/min时，4种模型的芯片温升与芯片热耗的关系如图6所示。

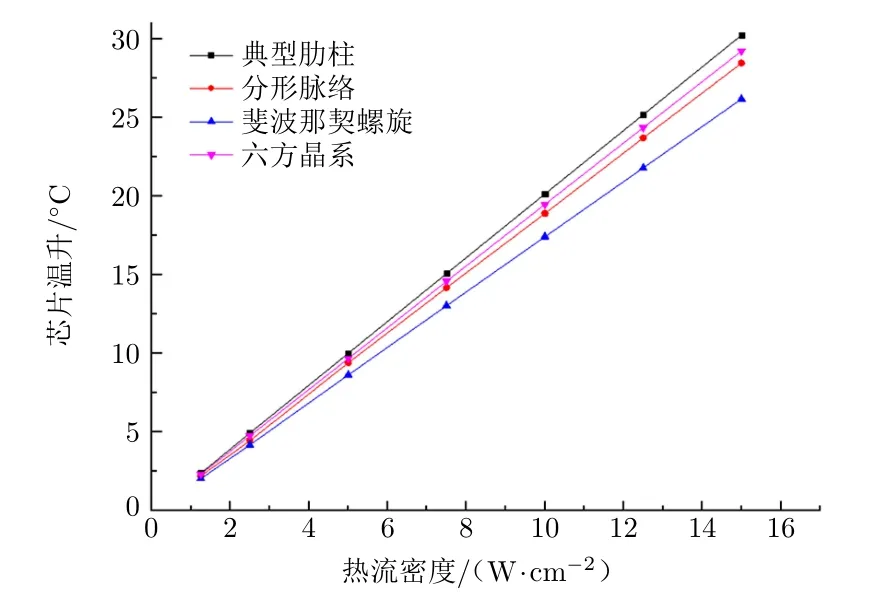
图6 芯片温升与热流密度的关系

从图6可以看出，芯片的温升与热流密度成正比，随着热流密度的增加而增加，但整体温升并不高。当热流密度≤15.6 W/cm2时，芯片的壳温依然保持在85◦C以下。

2.4 综合性能分析

分析散热性能时，还应对散热系统正常工作时的综合性能进行衡量。本文以散热系统在运行过程中所需消耗的泵功率为基础，对4种模型的综合性能进行分析，其中泵功率W的计算公式为：

式中：∆p是冷却介质在模型中的压力损失；V是冷却介质的体积流量。

芯片温升与泵功率的关系如图7所示。

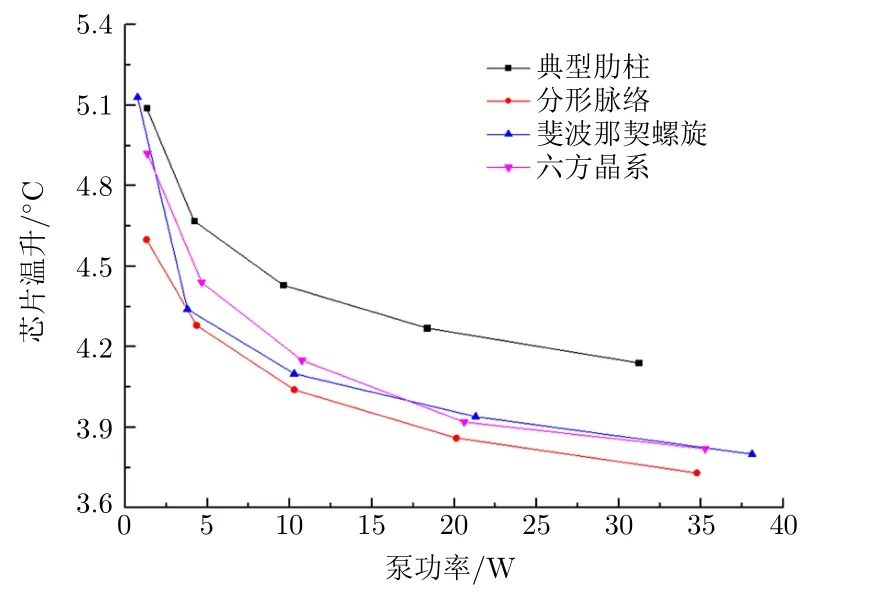
图7 温升与泵功率的关系

从图7可以看出，芯片温升随着泵功率的增大而减小，变化趋势渐渐平缓，说明一直提高泵功率对提升换热性能的作用变小。通过对比发现，在泵功率相同的情况下，典型肋柱模型的温升最高，斐波那契螺旋和六方晶系模型相差不大，分形脉络模型的温升最小，综合性能最佳。

3 应用及测试

3.1 贯通式VPX模块

VPX总线标准具有带宽高、通用性强、抗恶劣环境能力强等优点，代表着新一代军用综合信息处理平台系统的发展方向。贯通式液冷模块是指通过TSF盲插流体连接器直接将冷却介质贯通至模块冷板内部。为解决高热耗VPX处理模块的散热问题，文中基于某热源分布，设计了一种贯通式液冷VPX模块，并将仿生微通道耦合射流系统应用于该模块。

高热耗的VPX处理模块一般由载卡和子卡组成，位于载卡与子卡之间的导热板厚度往往只有3 mm左右。将流道布置在中间板不仅流阻大，散热性能也很难达到要求。本文将处理模块的子卡盖板设计为贯通式液冷冷板，通过蛇形流道将2个微通道耦合射流系统相互并联。目前加固型VPX电连接器未集成液体连接器，且电连接器占据了标准模块宽度233.35 mm的所有空间，故本文将TSF流体连接器设计在盖板上方，如图8所示。

图8 贯通式VPX模块

该模块采用结构化思维进行散热设计，以热耗大小为基础，自顶向下逐步细化。散热设计方法如下：

1）常规芯片热耗较低，通过模块底板或中间板传导至模块导轨，再通过锁紧条压装贴合传导至液冷冷板。

2）子卡的AD芯片热耗较高，通过导热衬垫贴合液冷上盖板，将热量传递给冷却介质。

3）载卡的FPGA处理芯片的热耗最高，通过仿生微通道耦合射流系统进行强化换热。

3.2 测试及分析

为了验证数值模拟方法的准确性以及测试仿生模型的散热性能，设计了一套试验系统。采用陶瓷加热片模拟FPGA芯片，发热源尺寸为30 cm×30 cm。通过驱动微型泵带动冷却介质流动，液体从泵的出口出来，经过流量计、温度计后进入贯通式冷板与模拟芯片进行热交换，换热后的流体工质进入冷凝器，最后回流至水箱。

试验中泵功率恒定在5 W，得到的不同功耗下的芯片温升见表4。

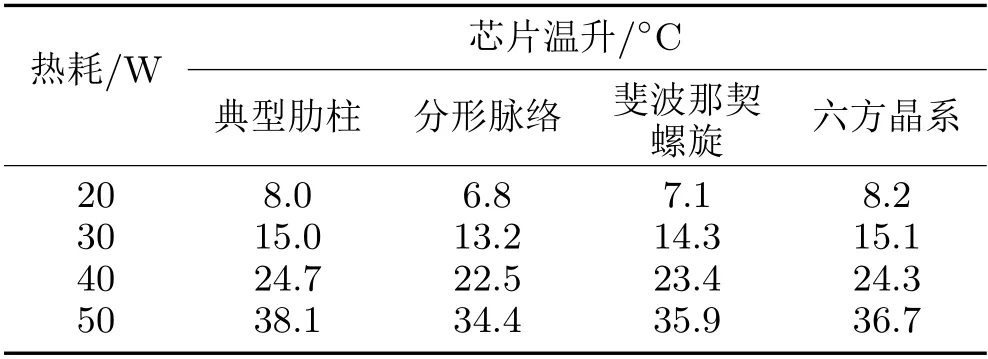
表4 4种模型不同功耗下的芯片温升

从表4可以看出：在泵功率相同的情况下，典型肋柱模型的相对温升最高，分形脉络模型的相对温升最小，其余两者随着芯片热耗的上升互有交替，试验结果与仿真结果保持一致。

芯片热耗为40 W，热流密度为4.4 W/cm2时，试验测得的典型肋柱和分形脉络模型的芯片温升相差2.2◦C，仿真计算得到的两者的温升相差2.6◦C。测试结果与仿真结果的相对误差为0.4◦C，验证了数值模拟计算的准确性。存在相对误差的主要原因在于：1）试验中的平均温度是布置于底板的2根热电偶的平均温度，与数值模拟中直接求取的底面的平均温度存在一定的误差；2）试验中热源和贯通式冷板与周围空气还存在一定的对流换热和辐射换热，而仿真中采用的是绝热界面。

综上所述，试验验证了仿真计算的准确性，进一步说明了仿生微通道耦合设计系统有着强大的换热能力。

4 结束语

本文设计和研究了3种基于仿生学的微通道耦合散热器，为突破电子设备散热瓶颈和热控技术的发展奠定了基础。其主要研究成果如下：

1）借助自然界中具有代表性的3种管网结构设计了分形脉络、斐波那契螺旋和六方晶系仿生微通道耦合射流散热模型。

2）通过仿真分析得知，3种仿生模型的散热性能都优于典型肋柱模型；在Re一致的情况下，斐波那契螺旋模型的平均Nu最大，换热性能最佳；在泵功率一致的情况下，分形脉络模型的平均温升最低，综合性能最好。

3）设计了一种贯通式液冷VPX模块，并将仿生微通道耦合散热系统应用其中，通过试验验证了其仿真计算结果与试验结果的一致性，进一步论证了仿生微通道耦合射流系统的散热性能。