相对变化值参考区间新算法的建立及应用评价
2021-06-26李丹杰唐大海刘曼娇贺嘉蕾蒋梦洁韦晓强
岳 波,李丹杰,唐大海,刘曼娇,贺嘉蕾,蒋梦洁,韦晓强
(上海长海医院虹口院区检验科,上海 200081)
1983年,Harris和Yasaka提出参考变化值(reference change value,RCV)的概念[1],尝试创立一种用于评估单个病例连续检测结果之间差异有效性的客观的工具,由此拉开个性化解读检验结果的序幕。当患者当前检测结果(X2)与上一次检测结果(X1)之间的相对变化值[ΔR,ΔR=(X2-X1)/X1]超出RCV时,则认为变化有效,提示患者健康状态发生变化,否则认为变化无效,变化源于固有变异[CVT,CV为变异系数(coefficient of variation)][2]。RCV有助于临床更客观地评估患者健康状态的变化,减少因临床医生认知局限和主观意识偏差对病情判断的干扰。RCV在我国一直被译为“参考变化值”,然而相关文献[1-7](包括Harris本人)均认为RCV的定义是“在患者健康状态未发生明显改变时,由相对变化值ΔR的所有可能值组成的集合的中间95%部分构成的区间”,或称相对变化值ΔR的95%参考区间(confidence interval,CI),因此我们认为,将RCV翻译为“相对变化值参考区间”更易于理解和推广。
理论上认为,患者当前健康状态的指标有一个相对平衡点(稳定值),平衡点发生改变,则提示健康状态发生改变,如能检测平衡点,则可较好地评估健康状态变化。然而,由于个体内生物学变异(CVI)的存在,患者指标时刻都在变化,每次对平衡点的检测实际只是对围绕平衡点变化的各种可能值组成的总体的随机抽样。另外,标本的检测结果还受分析变异(CVA)影响,因此最终测定的关于平衡点的结果等效于对由围绕平衡点变化的各种表观测量值组成的总体的一次随机抽样(图1),该总体的变异由CVI和CVA叠加而成,且无法消除,被称为固有变异(CVT)。当CVT较大时,即使平衡点未发生明显改变,每次的测量值之间也可能存在较大差异,因此临床医生在监测治疗效果及疾病转归时,迫切需要一种方法来判断“当前检测结果(X2)与上一次检测结果(X1)之间的差异是否能说明病情发生了变化,差异是否仅源于CVT”。
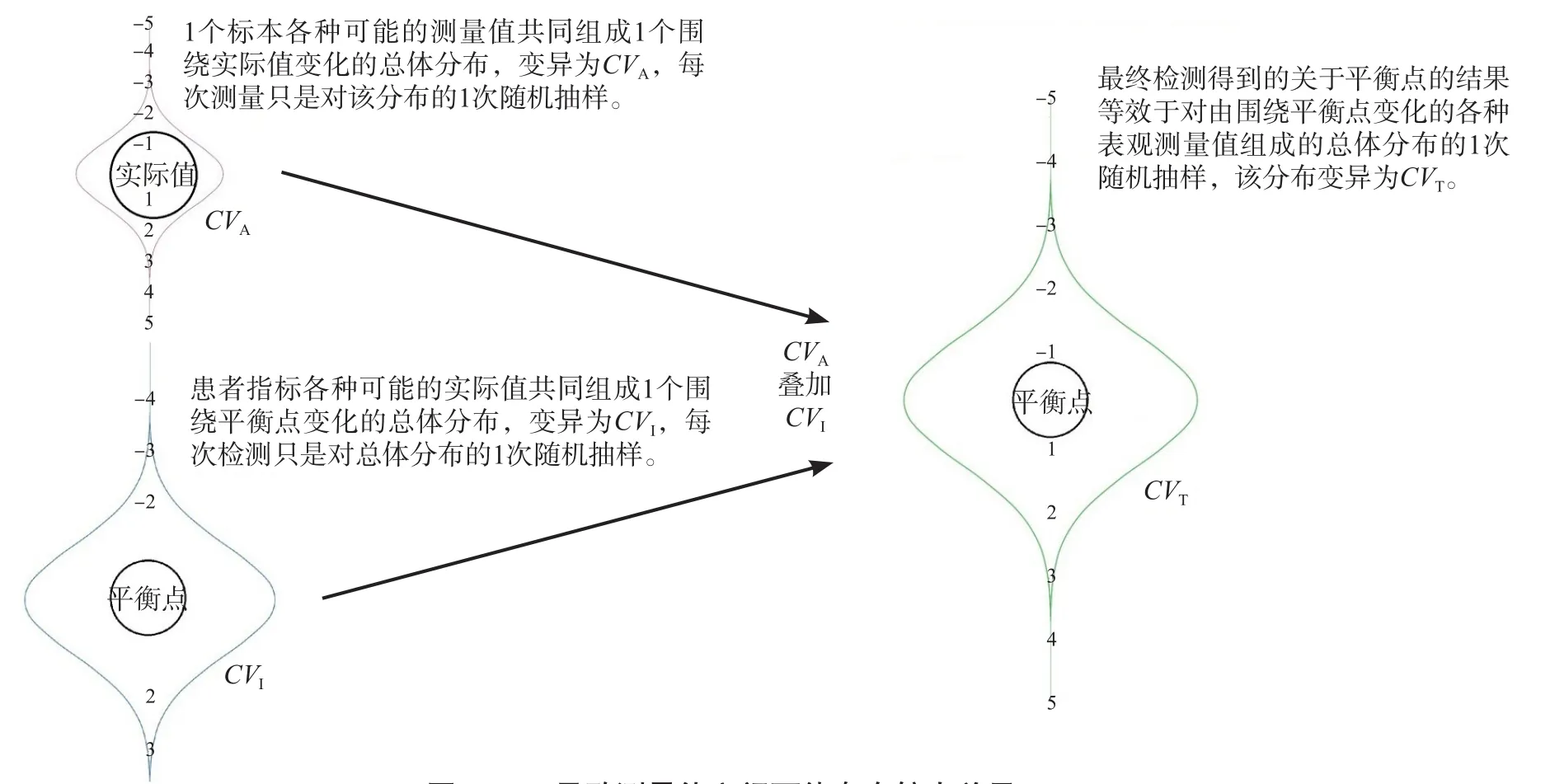
图1 CVT导致测量值之间可能存在较大差异
换一种方式分析这个问题:将患者当前健康状态所有可能的检测结果放在一起,组合成总体(T),变异为CVT,每次从T中随机连续抽出2个数据Xi1、Xi2,设ΔRi=(Xi2-Xi1)/Xi1,将全部的ΔRi放在一起,组合成ΔR分布,上述问题即转变为“已知CVT,求ΔR分布的95%CI,即RCV”。虽然Harris和Yasaka曾给出计算公式[1]:为一种对称性区间,但我们认为该算法欠妥。我们的研究结果显示,ΔR呈正偏态分布,而非正态分布,其他学者也有相关研究结果支持正偏态分布[8-12]的结论,因此RCV应具有非对称性,RCV算法需要改进。为此,基于蒙特卡洛法,我们采用Excel 2007软件进行了大数据建模,对ΔR的分布特点及其与CVT的关系进行了系列分析,为了便于研究,我们引入了本研究团队近年来推广的波动性(λ,λ=X2/X1)及波动性参考区间(CIλ)等指标[13-14]。
1 材料和方法
1.1 研究对象
基于蒙特卡洛法建立的统计学模型,包括用Excel 2007软件建立的大数据正态分布模型、λ分布模型、ΔR分布模型。
1.2 方法
先通过蒙特卡洛法得到符合条件的随机变量,建立模型,再用统计学方法分析模型中各种特征变量及不同变量相互之间的关系。
(1)假设同一健康个体多次检测结果的数值相互独立,没有相关性和趋势性,且呈正态分布。定义相邻2次检测结果的前1次结果为X1,后1次为X2,计算公式为:λ=X2/X1,ΔR=(X2-X1)/X1,CIλ、RCV分别为λ和ΔR的95%CI。
(2)此次建模主要使用了3个函数:①“NORMDIST(0,μ,σ,1)”函数可返回0在正态分布中的累积概率,为使产生的随机变量呈非负值,并尽可能保留正态性及完整性,我们在0的右侧非常靠近0的位置进行了截断,截断下限对应的累计概率设置为“NORMDIST(0,μ,σ,1)*1.000 000 1”,上限与之对称,为“1-NORMDIST(0,μ,σ,1)*1.000 000 1”;②“RAND()*(b-a)+a”函数可返回a和b之间的随机数,在本模型中用于从正态分布中进行随机抽样,a和b分别等于①中的下限和上限对应的累积概率;③“NORMINV(P,μ,σ)”函数可返回给定累积概率在正态分布中对应的区间点,令P等于②中计算出的概率,即可从正态分布N(μ,σ2)中进行1次随机抽样。合并后的复合函数为“NORMINV(RAND()*(1-NORMDIST(0,μ,σ,1)*1.000 000 1*2)+NORMDIST(0,μ,σ,1)*1.000 000 1,μ,σ)”。该复合函数通过稳健处理法[8,15]将正态分布N(μ,σ2)在0和2μ附近对称性地截断,然后从中随机抽样,确保模拟变量的随机性、非负性、正态性。首先使用复合函数在A、B 2列生成100万对非负数据,模拟健康个体多次检测结果,A列模拟相邻2次检测结果的前1次结果(X1),B列模拟后1次结果(X2);C列模拟λ,值为X2/X1,共100万个;D列模拟ΔR,值为(X2-X1)/X1,共100万个。
(3)不断改变μ、σ、CV的取值,分析λ和ΔR的变化规律,同时绘制频数分布折线图进行比较,必要时使用SPSS软件辅助正态性检验。
(4)将μ固定为1 0 0,σ通过公式“100*CV”自动计算,先将CV设置为0.1%,利用非参数法统计C列、D列的95%CI(即CIλ和RCV)并记录。然后将CV设置为0.2%,再统计相应CIλ、RCV,并记录。CV每次以0.1%递增,重复上述步骤直至CV为30.0%,得到共300组数据,汇总结果并绘制与CV对应的关系表。
(5)对300组CIλ、RCV与CV的对应关系进行回归分析,得出RCV的回归方程及新算法。
(6)使用新算法重新计算既往文献[16-17]报道的RCV应用实例数据,并与传统算法进行比较。
1.3 相关公式及推论的证明
(1)根据λ和ΔR的定义可知:λ=X2/X1,ΔR=(X2-X1)/X1,因此ΔR=(X2-X1)/X1=X2/X1-1=λ-1,即ΔR=λ-1(公式1)。
(2)将正态分布模型进行u变换,设ui=(Xi-μ)/σ,则ui呈标准正态分布,即ui~N(0,1)。由ui=(Xi-μ)/σ可得Xi=uiσ+μ,所以λi=Xi2/Xi1=(ui2σ+μ)/(ui1σ+μ)=(ui2+μ/σ)/(ui1+μ/σ)=(ui2+1/CV)/(ui1+1/CV),即λi=(ui2+1/CV)/(ui1+1/CV)(公式2)。
(3)设λi=Xi2/Xi1,因为Xi1和Xi2的抽样是随机且相互独立的,所以在1次配对抽样中,抽取组合(前1次结果为Xi1,后1次为Xi2)的概率与抽取组合(前1次结果为Xi2,后1次为Xi1)的概率相等,即在λ分布中,λi和1/λi出现的概率相等。对λ进行自然对数转换,则ln(λi)与ln(1/λi)在lnλ分布中出现的概率相等。由于ln(1/λi)=-ln(λi),所以ln(λi)和-ln(λi)出现的概率相等,即lnλ呈对称分布(推论1)。
1.4 统计学方法
采用Excel 2007和SPSS 24.0软件对λ、ΔR的分布进行统计学分析。采用2种方法进行正态性分析。(1)Z分数法。Z分数是以标准差为单位对原始数据与均值之间距离度量的指标,通过变换公式,可将分析对象转换为Z分数,当原始数据呈正态分布时,则Z分数呈标准正态分布。(2)K-S检验法。将分析对象的Z分数频数分布折线图与标准正态分布进行比较,两者拟合度越高,分析对象呈正态分布的可能性越大,对于拟合度较高者采用第2种方法做进一步检验。根据EP28-A3c指南要求[16],非正态分布数据使用非参数法(P2.5,P97.5)确定95%CI。
2 结果
2.1 λ和ΔR的分布特点及相互关系
由公式1可推出:λ和ΔR可互相转换,两者分布形状相同,将λ分布向左平移“1”即可得到ΔR分布,将CIλ的上限、下限同时减“1”即可得到RCV。频数分布图显示:λ、ΔR分布形状相同,且呈正偏态分布(图2),随着CV的增大,λ、ΔR分布的偏态越来越明显和扁平。λ的Z分数分布图显示:λ对应的Z分数分布峰值均在标准正态分布左侧,且尾部向右侧延申,即呈正偏态分布,且CV越大,偏态越明显(图3);当CV相同时,即使μ、σ相差很大,λ对应的Z分数分布图也基本能重合(图4),即λ的分布仅由CV决定,通过公式2也可证明此观点。

图2 不同CV时λ分布和ΔR分布比较
图3 不同CV时λ的Z分数分布

图4 相同CV、不同μ、σ、λ时Z分数分布
2.2 λ取自然对数后正态性分析结果
Z分数分布图显示,λ取对数后呈中心对称分布,且CV越小,lnλ的Z分数分布与标准正态分布拟合度越高,当CV≤9.5%时,分布图接近重合(图5),lnλ近似呈正态分布。

图5 CV为9.5%时λ、lnλ时Z分数分布
2.3 非参数法CI的校正
由推论1可知,λ取自然对数后呈以0为中心的对称分布,因此计算CIλ时将λ取对数后,取中间95%部分作为95%CI更科学。理论上lnλ分布的P2.5(lnλ)与P97.5(lnλ)以0为中心对称分布,但由于抽样误差的存在,实际统计分析出来的P2.5(lnλ)与P97.5(lnλ)很难对称,导致理论上呈对称性的CI,在采用非参数法进行统计时失去对称性。为保留CI的对称性,并降低抽样误差,我们使用校正因子(FC)对P2.5和P97.5进行校正:令FC=(|P2.5(lnλ)|+|P97.5(lnλ)|)/2,或者FC=(|ln(P2.5(λ))|+|ln(P97.5(λ))|)/2(公式3),则CIλ=(e-FC,eFC)(公式4),RCV=(e-FC-1,eFC-1)(公式5)。
2.4 建立FC、CIλ、RCV与CV的对应关系
由公式2可知λ的分布特征仅由标本总体的CV决定,因此CV的取值决定了CIλ、RCV,通过公式3、公式4、公式5可将CV、FC、CIλ、RCV相互之间建立一一对应关系。以0.1%作为间隔,我们模拟研究了CV为0.1%~30.0%时共300组对应关系,各组对应关系均先由模型生成100万对数据(数据容量越大,FC越稳定,当数据达到20万对时,已能维持FC精确到10-4时相对稳定,再继续增大数据容量意义不大。另外,受Excel 2007最大行数限制,模型数据容量设为100万对),然后再统计分析得出FC、CIλ、RCV与CV的对应关系。部分结果见表1。
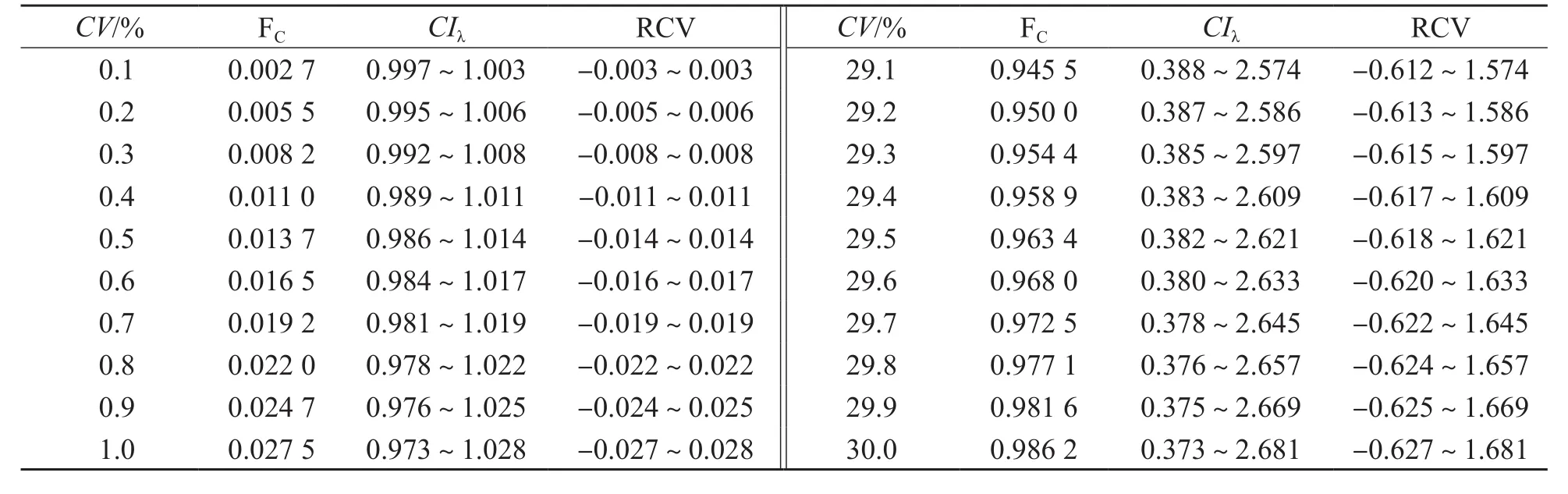
表1 CIλ、RCV、FC与CV的对应关系
2.5 对应关系的回归分析
利用Excel 2007软件对300组CV和FC的对应关系进行回归分析,结果显示,四次多项式拟合效果最佳,相关系数接近1.00。回归方程为:FC=15.14CV4-0.548CV3+0.620CV2+2.742CV(公式6);CV=0.032FC4-0.096FC3+0.006FC2+0.36FC(公式7)。
2.6 新算法与传统算法的应用分析比较
既往文献报道[16-17]中的RCV实例经本算法修正后,RCV区间均向右偏移,这种现象在CVT较大时更为显著。见表2、图6。
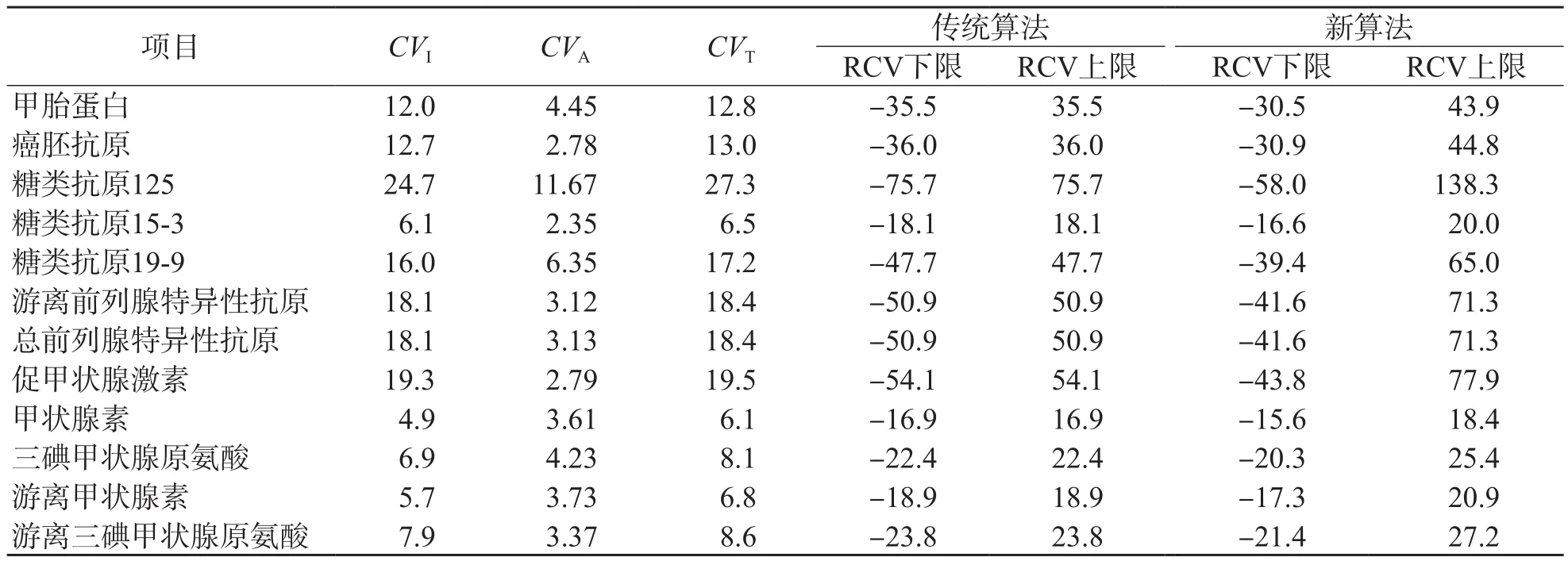
表2 2种算法RCV结果比较 %
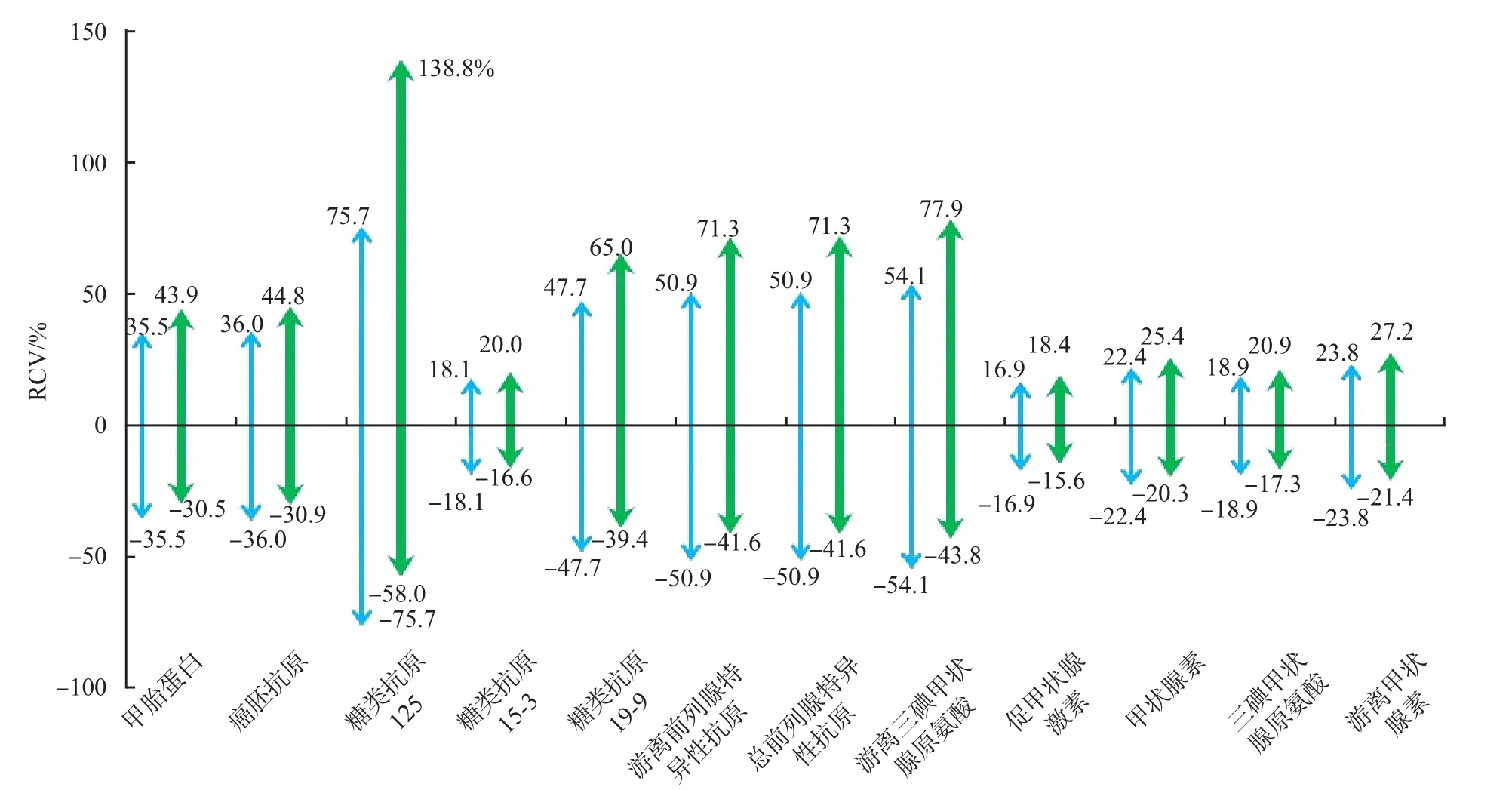
图6 2种算法得出的RCV的比较
3 讨论
λ和ΔR均涉及到2个正态变量之间的比值,分布较为复杂,目前尚无相关文献可以给出相关概率分布公式。本研究使用蒙特卡洛法模拟建立了由患者各种可能的表观测量值组成的、变异为CVT的总体分布模型和相关的λ、ΔR分布模型,再用统计学方法分析模型中各特征变量之间的关系,最后通过回归分析法得出RCV回归方程及新算法。
综合本研究结果可得出以下结论:(1)λ分布呈正偏态分布,取自然对数后呈中心对称分布,当CV≤9.5%时,λ近似呈对数正态分布;ΔR的分布与λ相同,位置相对于λ向左平移“1”,λ与ΔR可由公式1互相转换;(2)由正态分布总体衍生的λ分布均可由公式2转换为标准形式,即λi=(ui2+1/CV)/(ui1+1/CV),由于ui2、ui1均呈标准正态分布,因此λ分布仅由CV决定,若CV相同,则λ分布相同;(3)由推论1可知,λ取自然对数后呈对称分布,在使用非参数法统计分析CIλ和RCV时,引入校正因子FC可有效降低抽样误差,通过本研究的公式3、公式4、公式5分析CI更可靠;(4)公式6、公式7可以将CIλ、RCV经FC与CV相互转换;(5)回归分析结果显示CV越大,CIλ、RCV的范围越宽。
当通过RCV判断患者某指标检测结果从XA到XB的健康状态是否发生改变时,或检测结果从XB到XA的健康状态是否发生改变时,依据传统算法导出的对称性RCV可能会得出2个相互矛盾的结论,如假设某指标的CVT为12.8%,依据传统算法则RCV为(-35.5%,35.5%),假设140和100是患者的2次随机测量值,如果患者检测结果从140降到100,则ΔR=(X2-X1)/X1=(100-140)/140=-28.6%,未超出RCV,提示变化无效;如果患者结果从100升到140,则ΔR=(X2-X1)/X1=(140-100)/100=40%,超出RCV,变化有效,提示患者健康状态发生改变;同样的2个测试结果,只因出现顺序不同却得到2个互相矛盾的结论,因此传统算法得出的RCV欠妥。本研究的新算法则不会出现这种相互矛盾的结论。因为判断ΔR是否超出新算法导出的RCV区间,等同于判断λ是否超出CIλ,即等同于判断lnλ的绝对值是否超出F,而从XA到XB与从XB到XA2个方向变化得出的lnλ互为相反数,绝对值始终相等,所以依据新算法导出的RCV在从2个方向判断患者健康状态是否发生改变时,可以始终保持一致。依据新算法,此例中的RCV为(-30.5%,43.9%),FC为0.364 0,判断从2个方向得出的ΔR是否超出RCV等同于判断ln(100/140)及ln(140/100)的绝对值是否超出FC,很显然,|ln(100/140)|=|ln(140/100)|=0.336 5未超出0.364 0;而-28.6%与40.0%也均未超出(-30.5%,43.9%),即无论结果从140变化到100,还是从100变化到140,都提示变化无效,变化可能源于固有变异(CVT),患者健康状态未发生明显改变。由于计算RCV的原理不同,与传统算法相比,新算法得出的RCV改变较显著(表2和图6),有助于RCV的临床推广应用。
1983年,Harris和Yasaka就提出通过ΔR是否超出RCV来评估结果变化是否有统计学意义[1],但直至目前,RCV的概念和应用却极少被用于临床实验室,我们认为有以下原因:(1)研究RCV的大部分学者认为ΔR呈正态分布,RCV是对称的,然而本研究结果显示ΔR呈非对称的正偏态分布,因此RCV计算公式的适用性存疑;(2)RCV计算公式中的CVT需要根据个体内生物学变异(CVI)来计算,而现有文献报道的各种CVI通常来自少数人的、小样本量的数据统计分析,重复性差,不具代表性,同一指标的CVI在不同文献[19]报道中往往差异很大,给RCV计算带来困扰。上述2点是RCV在临床应用中的最大阻力。近几年,我们提出通过λ是否超出CIλ来评估结果变化是否有统计学意义,在临床应用上取得了一定进展[13-14]。与ΔR相比,λ为非负数,可进行对数转换,有利于分布特征的分析。在公认的、统一的、标准的CVI检测方法出现之前,通过本研究的公式3、公式4、公式5进行非参数法统计CIλ、RCV,结果更可靠,更适合进行临床推广应用。
有研究结果显示,由于生物学变异及分析变异的影响,仅依靠传统CI解读实验室检测结果存在较大局限性[13-14,20]。CIλ、RCV以及CVI的研究是精准解读实验室检测结果,提高实验室信息在临床决策过程中的影响力的关键一环。遗憾的是,关于这些指标的研究目前仍没有标准化的统一方案,亟需更多力量、更多学科相互合作,去研究和推动。
本研究是蒙特卡洛法在检验医学中的一次运用,随着科技的进步及跨专业医学人才的不断涌现,希望会有越来越多的交叉学科的知识融入医学,助推医学进步。
