考虑形状差异的RFS 多目标跟踪性能评估方法

王碧垚，王永齐，顾 鹏

（中国电子科技集团公司第二十九研究所，成都 610036）

0 引言

多目标跟踪是雷达、电子侦察、导航、空中交通管制等设备/系统数据处理中的重点内容之一，其跟踪性能的好坏对系统整体性能有着非常重要的影响。近年来，随机有限集（RFS）统计学理论作为一种友好的贝叶斯理论工具被广泛关注，基于RFS 的多目标跟踪方法成为研究热点［1］，该方法不同于传统的基于数据关联的多目标跟踪方法，对其进行性能评估时不适合采用均方根误差指标。

针对RFS 多目标跟踪评估问题，文献［2］率先给出了多目标系统下脱靶距离的定义与性质，提出使用Hausdorff 距离和最优质量转换（Optimal Mass Transfer，OMAT）距离对跟踪性能进行综合评估，并对比了两者在势不一致时的敏感程度。Schuhmacher等人［3］分析了文献［2］中两种距离的缺陷后提出了OSPA 距离，引入一个可调参数来控制位置误差和势误差的惩罚程度，提高了评估的灵活性。文献［4-5］注意到跟踪器输出的航迹通常为带标签的时间序列，于是引入航迹标签误差后，采用标签OSPA（Labeled OSPA，L-OSPA）距离进行评估。文献［6］强调了协方差信息在滤波中的重要性，提出在计算OSPA 距离时使用Hellinger 距离替代欧氏距离。文献［7］利用多目标状态估计器提供的航迹质量信息在OSPA 距离上改进得到了Q-OSPA 距离，并指出当分配每个估计器相同质量时Q-OSPA 就退化为OSPA 距离。文献［8］考虑了航迹错误、丢失、漏检等现象后，在OSPA 距离基础上提出了一种更完备的评估方法。Beard 等人基于OSPA 距离直接在航迹空间中引入时间权重，构造出OSPA（2）距离，证实了OSPA（2）完全满足公理化特性并能综合反映航迹断裂和航迹切换问题［9］，最后说明了OSPA（2）的优势和其局限性［10］。国内学者也对该问题进行了研究，文献［11］在充分考虑虚假估计和漏检目标问题后，对OSPA 距离进行了修正并验证了修正后指标的合理性。文献［12-13］通过实例详细分析了圆丢失率、Wasserstein 距离、Hausdorff 距离、OMAT 距离、OSPA距离以及L-OSPA 距离等指标的特点和适用场合。

上述文献提出的OSPA 距离及其各种改进/修正形式均没有考虑目标间可能存在的几何形状信息，而在部分多目标跟踪场景中，如编队飞行目标、协同作战目标等，这时目标点组成的形状信息对作战意图理解、威胁估计有着重要的意义，因而在性能评估时，理应考虑对该形状差异的度量。为解决这一问题，提出了一种考虑形状差异的改进OSPA 距离，并基于傅里叶描述子给出了形状差异度量的计算公式，仿真表明所提改进方法提高了评估的完备性。

1 问题描述

1）当多目标存在某种协同运动关系时，其组成的形状图也是非常重要的信息，而滤波器B 在跟踪时具有较高的形状保持能力，根据它的跟踪结果得到的态势图，更利于指挥员对作战要素的行为意图作出更加准确的理解和判断；

2）滤波器B 的跟踪结果组成的几何形状相比真实形状，几乎可以认为出现了整体偏移，那么滤波器B 就存在潜在的可矫正性，即借助其他传感器或者信息引入某种误差配准算法对跟踪结果进行矫正，从而可以减小每个目标的位置误差。

因此，是否可以考虑引入某种形状误差的度量构造新的OSPA 距离，使其在传统OSPA 距离的基础上，还能反映估计出的目标几何形状与真实目标几何形状之间的接近程度，对滤波器进行全面评估或比较，为评估人员提供更加有效的结论。

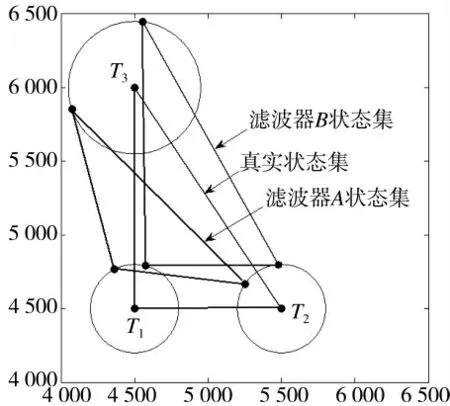
图1 目标真实状态和滤波器估计状态

2 OSPA 距离

截止参数c 可以理解为用来决定势误差（目标数估计误差）部分相对于位置误差部分的权重。c 越小，表示越关注位置误差，c 越大，表示越关注势误差。文献［3］论证了OSPA 距离作为度量指标满足3个度量公理，并且关于计算OSPA 距离的程序实现给出了两种具体方法，不再赘述。

3 改进的OSPA 距离（F-OSPA）

3.1 F-OSPA 距离构造

为了解决第1 节描述的问题，构造出式（2）的一种改进形式：

显然新构造的F-OSPA 距离也存在局限性，并不适用于n≤2 的情况。

3.2 形状差异度的计算

在模式识别、图像处理领域，傅里叶变换作为频域分析的重要手段，通常用来进行形状表示、形状分析和特征识别、形状分类以及形状检索［14-15］，而傅里叶描述子（Fourier Descriptors，FD）作为形状边界曲线的傅里叶变换系数，可以描述多边形的形状边界，通过计算两个形状FD 的相似距离就可以表示其差异程度［16］。

将多目标位置组成的多边形边界表示为顺序连接的点，每个点K 用复数表示为弧长s 的函数［15］：

假定边界有M 个点，则边界可视为M-1 个线段的连续累加。令sk为点K 沿边界到参考点之间的弧长，则

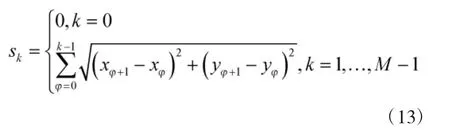
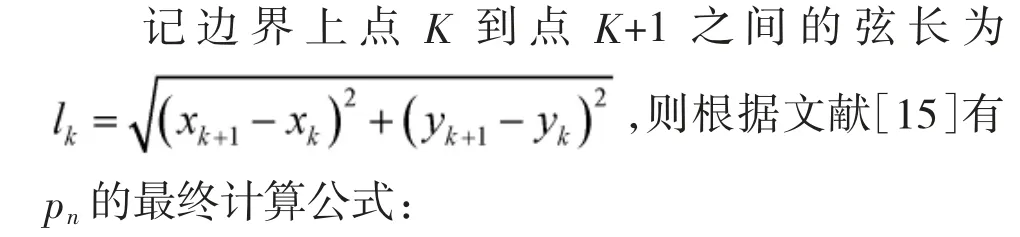
其中，An和Bn分别表示为

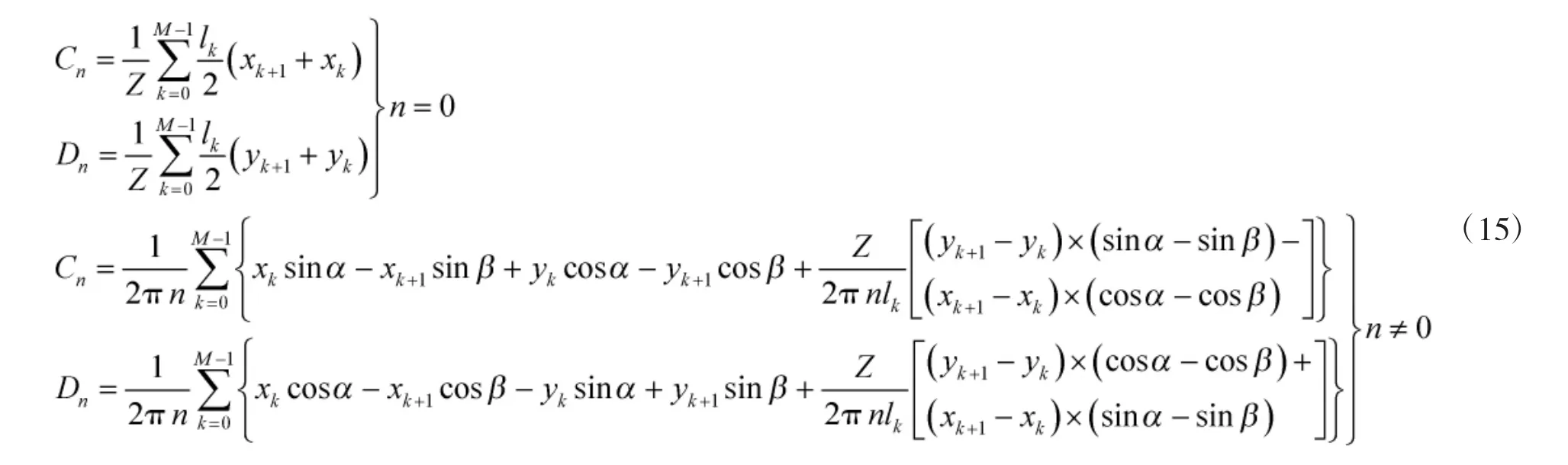
4 仿真与分析

4.1 F-OSPA 距离和OSPA 距离对比分析

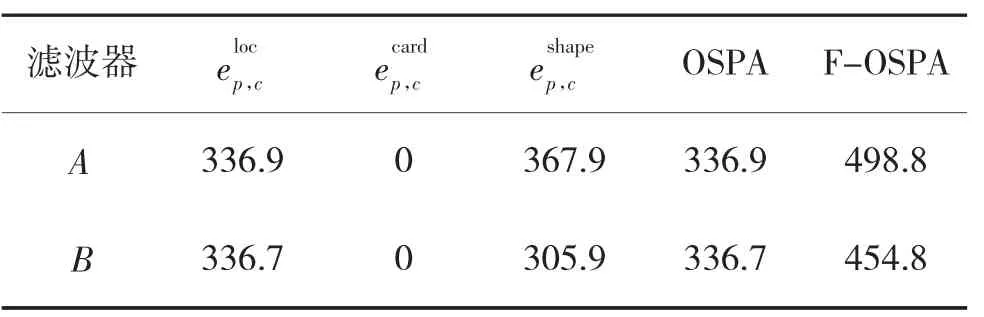
表1 F-OSPA 和OSPA 距离计算结果

由表1 中的计算结果可知，两个滤波器的OSPA 距离非常接近，几乎没有可分辨性，得出的结论自然是两个滤波器估计效果相当，但考虑形状差异后通过对比F-OSPA 距离可知，滤波器B 的性能明显优于滤波器A，这个评估结论更符合直观理解。F-OSPA 距离可以反映出滤波器在目标间形状估计方面的优势。

4.2 基于F-OSPA 距离的GMPHD 算法评估

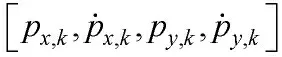
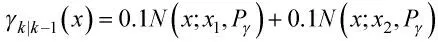
上式中新生目标的状态均值x1=［-600，10，500，0］T，x2=［-400，10，1 500，0］T，新生协方差阵Pγ=diag（［400，400，400，400］T），采用GM-PHD 滤波算法完成跟踪过程。具体的目标运动信息如表2 所示，目标运动真实轨迹见图2，显然即使此处是针对点目标的跟踪估计问题，但这些点目标形成的形状信息依然对态势理解有着重要意义。

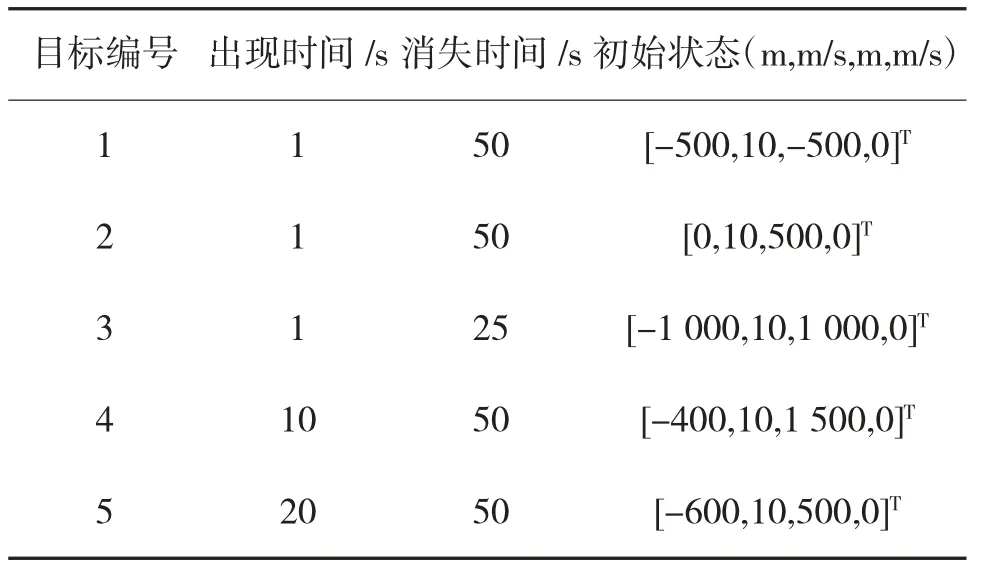
表2 目标运动想定信息

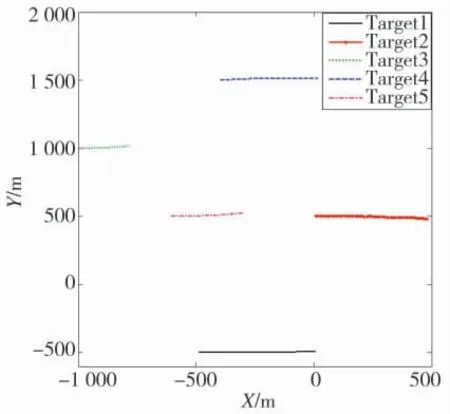
图2 目标运动轨迹

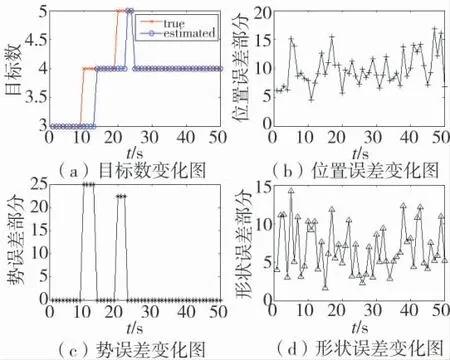
图3 各分误差结果

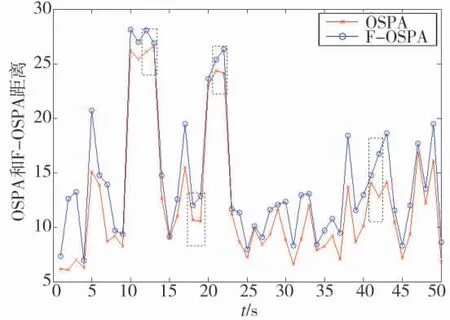
图4 F-OSPA 和OSPA 距离对比分析

结果分析：图3 给出了目标真实数目和估计数目比较结果以及F-OSPA 的3 部分误差，对于该仿真场景参数取为10 时，形状误差部分与其他两部分误差数量级相当。图4 比较了F-OSPA 距离和OSPA 距离，观察虚线框选出的部分可知，F-OSPA距离的变化趋势与OSPA 距离的变化趋势有时并不一致，因为F-OSPA 的变化趋势由3 类误差共同决定，而OSPA 距离的变化趋势只由两类误差决定，可见F-OSPA 距离可以提供更加完备的评估结论。需要说明，此处基于某单次仿真的结论分析，仅是为了方便阐述采用F-OSPA 距离进行评估的具体实施流程，并不是研究GM-PHD 滤波算法本身的优劣，而如果是研究算法性能，应该计算多次蒙特卡洛仿真下的平均F-OSPA 距离才有意义。

5 结论

本文针对随机有限集框架下多目标跟踪算法的性能评估问题，如协同作战目标等，提出了一种考虑形状差异的综合度量指标，即F-OSPA 距离。首先结合跟踪场景描述了采用OSPA 距离进行评估时可能不完备的情况，然后利用傅里叶描述子对形状的表达特性，提出了包含形状差异度量的F-OSPA 距离，并基于傅里叶描述子欧氏距离给出了形状差异度量的计算公式。仿真结果表明，F-OSPA 距离引入形状误差度量，弥补了仅包含位置误差和势误差的OSPA 距离的不足，针对部分跟踪评估需求可以提供更加完备的评估效果。