基于聚类选址的区域能源系统站网布局优化规划

王珊珊， 刘青荣*， 阮应君， 刘洪运

(1.上海电力大学能源与机械工程学院， 上海 200090； 2.同济大学机械与能源工程学院， 上海 200092)

近年来，随着社会经济的不断发展，能源需求不断增加，能源消耗所导致的环境污染问题日益严峻[1]。提高能源利用效率，减少污染排放成为解决能源与环境问题的关键[2]。区域能源系统因具有污染低，效率高等独特的优势，在世界范围内得到了快速的发展[3]。

区域能源系统包括能源站、供能管网和负荷需求点[4]。其中能源站的数量与选址对于整个系统的投资运营起了至关重要作用；另外，能源站与管网布局的相互耦合作用使得能源站选址问题更加复杂。因此在区域能源系统规划过程中，能源站数量、选址以及管网布局的综合优化是保障区域能源系统经济性的关键[5]。

目前，关于区域能源系统中设备运行规划方面研究较多[6-8]，而针对区域能源系统站网布局规划研究较少[9]。王瑞祥等[10]基于图论的思想提出了一种全能流城市能源网络规划方法，通过建立有向图和矩阵的结合通用模型，来分析比较不同路径组合的系统性能，较好地解决了多源多汇多路径的城市能源系统规划方法。Yan等[11]提出一种核密度估计和最短路径方法来优化传输管网，根据核密度估计方法确定供能站和储能站的最优位置，利用Astar搜索算法和筛选算法优化能源网络的分布，得到了投资和管网损失最小的能源站选址与管网布局模式，使网络总长度减少21.3%。易文飞等[12]结合p-中位模型建立了能源站选址及管网路径的优化模型，考虑负荷需求、能源站和管网的初始投资成本，并提出了一种基于枚举法的改进求解算法对规划模型进行求解。徐成司等[13]基于能流平衡约束和热网特性建立了区域综合能源系统的拓扑描述模型，考虑管线容量对成本的影响，利用正交多项式逼近等方法对优化模型进行简化求解，所提方法提高了问题求解的收敛性。陈娟等[14]提出“能距”的概念，建立了基于能距的p-中位模型，利用定址布网算法对能源站与储能中心的数量、选址和管网路径进行协同优化求解，为区域能源互联网实现整体最优架构提供了参考。王兆强等[15]应用最小生成树思想，在遍历解集空间中所有可行解后得到最优解，确定了能源站数量、选址和输送管网的最优路径。Jing等[16]提出一种基于层次的方法，利用聚类算法将整个空间划分为几个小区域，考虑负荷需求不确定性建立需求互补优化模型。结果表明与基线条件相比，项目成本可以节省42%以上，具有很高的实用价值。于震等[17]应用聚类分析和最小生成树算法对能源站选址及管网路由进行优化分析，总结出一种可定量计算评估的设计优化方法。

从中外研究现状来看，目前能源站选址一般通过工程经验进行判断和比选，确定备选能源站位置，然后依据算法从备选能源站中优选出最终的能源站位置与数量，缺少根据定性比较对能源站位置进行选优的研究。现提出一种将最短路径与聚类算法结合的规划方法，根据已知负荷点的负荷需求和规划区域道路分布情况，将能源站设置在靠近负荷中心位置，以系统年均经济成本最小为优化目标，建立区域能源系统站网布局优化规划模型，并通过算法对模型优化求解。

1 区域能源系统站网布局结构模型

区域能源系统的经济性与能源站数量、选址、管网布局紧密相关。在区域能源系统中，当能源站没有备选位置时，需在区域内确定能源站的最佳数量、位置、负荷归属及管网布局。聚类算法可以将整个区域划分,以此来确定能源站数目以及负荷归属，适用于区域能源系统能源站选址问题。在能源站选址的过程中，采用K-means聚类算法，将最终优化得出的聚类中心作为能源站选址，可以在优选能源站位置的同时确定负荷归属。另外采用最短路径算法确定能源站与负荷点间的管网布局，最终使区域能源系统的投资运营成本最小。

以区域能源系统能源站年均经济成本与管网年均经济成本之和最小化为布局规划的目标，其目标函数可表示为

(1)

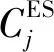
1.1 能源站经济成本

能源站的经济成本包括能源站的初期投资费用和后期维护管理费用，能源站年均经济成本可表示为

(2)

(3)

(4)

1.2 管网经济成本

管网的经济成本包括管网初期投资费用、折旧维护费用、水泵运行费用和供热管网的热量损失费用[18]，能源站j至负荷点i管网的年均经济成本可表示为

(5)

(6)

c(db)=9.484 6+4.942db

(7)

(8)

(9)

(10)

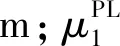
2 区域能源系统站网布局算法

K-means聚类算法通常采用两点间的直线距离作为相似性的评价指标，而在实际工程中管网布局一般是沿道路分布的。因此针对区域能源系统站网布局的实际情况，提出一种结合最短路径和K-means聚类算法的计算方法。该算法将最短路径思想引入K-means算法，参照最短路径确定能源站到负荷点的管网布局，并将能源站到负荷点的最短路径作为聚类相似性依据划分负荷归属，在确定能源站位置的同时确定了管网布局。相比于通过专家经验进行比选的能源站选址，该算法可以考虑负荷分布对能源站位置的影响，并且通过定性比较对能源站位置进行优选。算法结束时可以同时确定区域内最优的能源站数目、位置和管网布局。对于区域能源系统整个空间内设置一个或多个能源站的规划方案，该方法可以解决能源站数量、选址和管网布局问题。

算法总体思路：第一阶段采用Floyd最短路径算法得到聚类中心与负荷点间的最小权重矩阵D和对应的路径矩阵P；第二阶段将Floyd与K-means算法相结合，计算得到能源站位置、负荷归属和管网布局；第三阶段对不同数量的能源站，算法进行循环迭代；最终确定区域能源系统年均经济成本最小的能源站数量、位置以及管网布局。算法流程如图1所示。

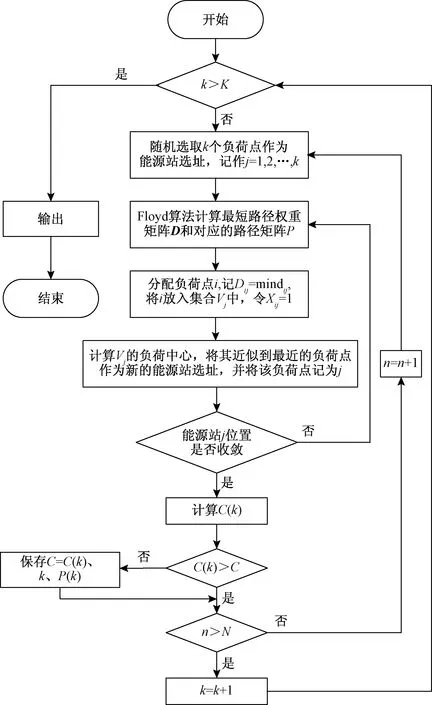
图1 站网布局算法流程图Fig.1 Flow chart of station network layout algorithm

算法流程如下(K为能源站数量上限，初始时设置k=1，C=∞，n=1，N=200)。

步骤1如果k>K，跳转至步骤13，否则，执行步骤2。

步骤2随机选取k个负荷点作为能源站选址，记作j=1，2,…,k。

步骤3采用Floyd最短路径算法计算能源站与负荷点间最短路径权重矩阵D和取得最小权重对应的路径矩阵P。

(11)

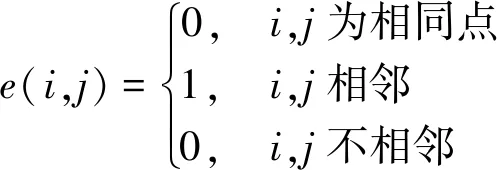
(12)

式中：dij是D的元素，其值为点i和j之间的最小权重。

步骤4分配负荷点i，对于j=1，2,…,k，比较dij；记Dij=mindij，将i放入集合Vj中，令Xij=1；重复计算，直至所有负荷点全部分配。

步骤5计算Vj的负荷中心，即

(13)

式(13)中：xj、yj表示能源站j所供应负荷点的负荷中心位置坐标；xi、yi表示负荷点i的位置坐标。将负荷中心近似到最近负荷点，并将该负荷点记为j，作为新的能源站选址。

步骤6如果新的能源站位置与旧的能源站位置为同一负荷点，则能源站位置收敛，执行步骤7，否则执行步骤3。

步骤7计算目标函数C(k)，即

(14)

步骤8比较C(k)与C的大小，若小于则执行步骤9，否则执行步骤10。

步骤9更新C=C(k)，并保存此时的能源站个数k、能源站位置、管网布局P(k)，并跳转至步骤10。

步骤10比较n与N的大小，如果n

步骤11n=n+1，并跳转步骤3。

步骤12k=k+1，并跳转至步骤1。

步骤13k>K时计算结束，输出能源站数量、能源站位置和管网布局。

3 案例分析

3.1 案例概况

选取浙江某区域规划数据进行计算。如图2所示，该区域共有30个负荷需求点，故能源站数量上限K设为30。道路节点共81个，编号为1～81；道路中间节点共97个，编号为82～178；负荷点共30个，编号为179～208。案例各负荷点的负荷需求如表1所示，案例仿真参数设置如表2所示。

表1 负荷点的负荷需求表Table 1 Table of load demand of load points

表2 仿真参数表[13,17,19]Table 2 Table of simulation parameters[13,17,19]

图2 案例区域道路节点图Fig.2 Road nodes map of the case area

3.2 站网布局规划结果与分析

在区域能源系统站网布局规划过程中，以系统年均经济成本最小化为目标，根据模型求解方法，利用MATLAB编写实现程序，完成站网布局的优化求解。算法通过设置不同聚类数目表示能源站个数，随机选取负荷点作为聚类中心，并将其记为能源站的选址，采用Floyd算法求解能源站与负荷点间路径矩阵，计算权重矩阵D；在计算的过程中，记录最小权重矩阵各节点间对应的路径矩阵P。根据最小权重矩阵确定各负荷点所归属的能源站，并对聚类中心循环迭代计算，使其靠近负荷中心位置。最终确定能源站的位置与对应的负荷归属信息，同时参照最短路径矩阵P，确定能源站与负荷点间的管网布局。

图3为不同数量能源站情况下，案例区域的系统年均经济成本、能源站年均经济成本和管网年均经济成本。从图3可以看出，随着能源站数量的增加，能源站年均经济成本增加，管网年均经济成本减少，区域能源系统年均经济成本呈现先减少后增加的趋势。当能源站数量为4时，区域能源系统年均经济成本最低。即能源站数量为4时，区域能源系统站网布局最佳。表3给出了最佳管网布局时能源站与负荷点之间的最短路径和能源站容量信息。

图3 不同数量能源站各项年均经济成本Fig.3 Average annual economic cost of different number of energy stations

表3 负荷归属、最短路径信息与能源站容量信息表Table 3 Table of load attribution, shortest path information and energy station capacity information

续表3

案例区域的能源站与管网布局最终优化结果如图4所示。图4中4个星形结点表示经K-means聚类和最短路径算法最终确定的能源站位置，即案例区域能源站数量与位置的优化结果；算法同时给出了能源站至负荷点的最优管网布局。从图4可以看出，该案例区域被划分为4个供能区域，每个区域由一个固定的能源站供能。

图4 区域能源系统站网布局优化结果Fig.4 Optimization results of district energy system station network layout

4 结论

研究了区域能源系统中能源站数量、选址和管网布局的规划方法，构建了以最小年均经济成本为目标的区域能源系统的站网布局模型。提出了将聚类算法与图论最短路径结合的求解算法，得出如下结论。

(1)所提出的基于聚类选址的区域能源系统站网布局优化模型，考虑了能源站、供能管网的初始投资与运营维护成本，适用于以经济性为目标的站网布局优化规划研究。

(2)所给的站网布局算法，在区域没有备选能源站位置的情况下，能够确定区域内最优的能源站数量、选址以及能源站和负荷点间的管网布局，实现区域能源系统站网布局优化规划。

(3)讨论了区域能源系统站网布局规划研究，主要考虑了区域能源系统内负荷点、能源站和枝状管网的布局优化，未来将进一步考虑多能流的源、荷、储、网的综合布局以及含有环状管网的布局优化问题。