大观念视角下的反比例意义教学
2021-06-25浙江省温州市滨江外国语小学林志辉
浙江省温州市滨江外国语小学 林志辉
浙江省温州市仰义第一小学 陈柯柯
教学内容:人教版数学六年级下册第47、48页。
反比例函数是重要的数学模型,体现了基本的函数思想,在数学思想层面上对以前所学过的许多数学问题和数学规律等进行一般化和模型化,对学生代数思维的发展十分有益。课程标准要求第二学段的正比例教学注重表格数据分析、图像分析和关系式概括,是一个完整的建模过程。而回顾小学阶段课程标准对反比例的要求,较为关注表格内数据分析与关系式概括,不要求出现反比例图像。反比例图像为一条光滑的曲线,学生确实较难通过描点法画图得到。但教学时反比例真的可以不需要图像吗?
一、教材对比中的数形需求
横向对比7个版本的教材,笔者发现人教版、苏教版和浙教版不约而同都提出了字母式和图像。其他版本教材虽然没有明确地提出字母式和图像,但定义描述时都提到了字母式的雏形。各版本教材不约而同引入了反比例的图像和关系式,由此可见引入图像是有必要的。
进一步对比7个不同版本的教材,虽然提供的学习素材不同,但都是结合具体情境来认识反比例关系,有些教材用足一个素材,有些教材则通过不同的素材比较,来帮助学生更好地理解反比例,判断两个量是否成反比例关系。 而对反比例的定义主要分成两种形式:结合具体例子和科学规范的定义。
因为之前学习了正比例,笔者认为学生已经有了一定的抽象概括能力,将一个素材用足,在科学规范的定义下,既能帮助学生对反比例函数有科学的认识,同时有利于培养学生的抽象概括能力。
二、学情分析下的数形需要
反比例函数是学生在学习完除法、分数、比、方程等数学知识后的综合与提升。在教学本堂课前,笔者思索学生对于成反比例关系的两个量到底有怎样的前情认知,所以在正式上课之前,进行了学习单的检测(如图1)。

图1
笔者对129个学生进行抽测,根据学习单,我们发现学生能借助图表发现简单的规律,A中画面积是12cm2的长方形,20.9%的学生能发现“宽变大,长反而变小”,41.9%的学生能发现A中长和宽的“积不变”。B中23.3%的学生能发现“宽变大,长随着变小”,46.5%的学生能发现“和不变”。由此可见,在学习完正比例的基础上,学生虽能关注到两个量之间的关系,但对于“积不变”的感悟是不深刻的,在量的关注上还需要教师进行引导,因此数形的引入就显得十分有必要。
三、数形结合下的模型建立
(一)初识数形特点,关注量的规律
1.探究“学习单A”量的规律
师:课前我们做了一份学习单,和你的同伴交流你发现的规律,记录你认同的新规律。
师:你猜她发现了什么规律。(如图2)

图2 学生作品一
生1:宽增加,长减少。
生2:长乘宽的积都是12。
师:为什么长和宽都在变化,而面积一直不变呢?
生:当宽乘2时,长除以2,就是积的变化规律。
2.对比“学习单B”量的规律
师:学习单B中的长和宽的变化规律和A中长和宽的变化规律有什么相同或不同的地方?(如图3)

图3 学生作品二
生:一个数增加,另一个数减少,相加所得的和都一样。
设计意图:学生通过“画图—填数—找规律—找异同”4个步骤探究面积是12cm2的长方形,周长是12cm的长方形。基于学习单A和B的对比,笔者发现学生都能用自己的语言结合图表发现学习单A和B中长和宽变化,学生的语言虽质朴,却能清晰地表达出学习单A与B中长和宽变化的异同点。通过第一次学习单的对比,学生对于两个量的变化规律有了一定的认识,为进一步学习反比例知识埋下了伏笔。
(二)建构数形对应,初步抽象模型
学生带着问题自学课本:
①怎样的两个量成反比例关系?
②A和B中的两个量成反比例关系吗?
师:像这样一个量增加,另一个量减少,这样的两个量在数学上成什么关系呢?
师:A表中的两个量是否成反比例关系?小组讨论。
生:A表中两个量成反比例关系,因为一个量增加,另一个量减少,且积不变。
师:(如图4)宽为1cm,长为12cm,宽为2cm,长为6cm,随着宽增加,长减少,而积始终不变。像这样的图像就叫反比例图像。
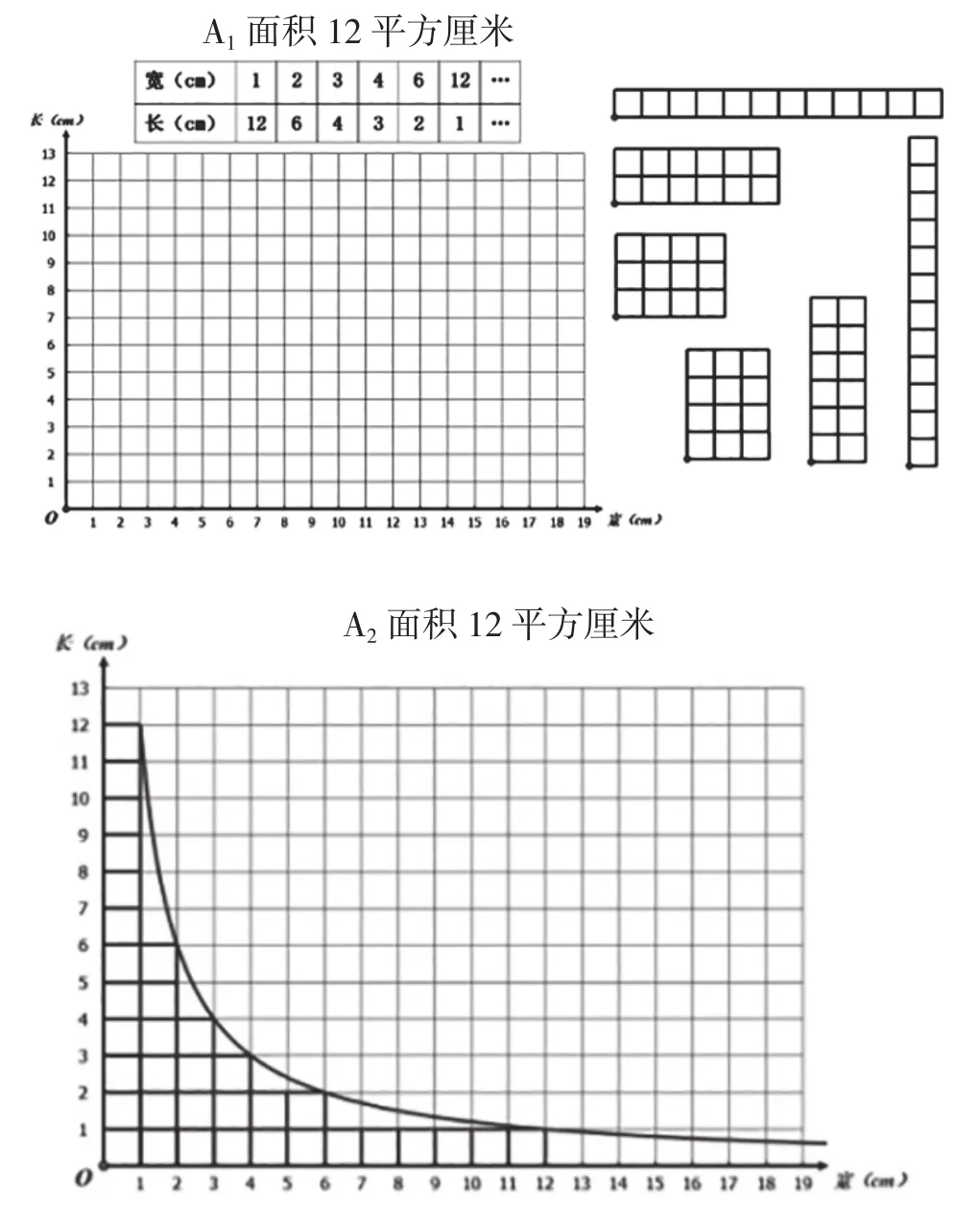
图4 几何画板演示反比例图像
师:B中,随着宽增加,长也减少,所以B中的长和宽成反比例关系,赞同的请举手。
生1:对,因为一个量增加,另一个量减少,所以这两个量成反比例关系。
生2:不对,虽然它们一个量增加,另一个量减少,但是它们的和是6,反比例要乘积一定,所以它们不成反比例关系。
师:到底怎样的两个量成反比例关系呢?
师:像这样宽增加,长减少,长和宽的积一定,我们就说长和宽成反比例关系。这就是反比例的图像和关系式。
设计意图:本环节学生经过三次对比,逐步促进了对反比例意义的理解。首先基于学生自学,对比学习单和书本课例,初步感悟反比例意义。再通过反比例对比量的变化规律,辅以课件呈现图像对比,进一步对比量之间的关系,抽象出关系式,初步建立反比例模型。
(三)对比数形特征,深化比例模型
师:长为6cm,宽和面积成反比例关系吗?(如图5)

图5 课件呈现宽和面积成正比例的数量
生:不是,成正比例关系。
师:谁能说一说怎样的两个量成正比例关系?还记得正比例的图像吗?比一比。
生:一个量增加,另一个量也增加,且商不变,这样的两个量成正比例关系。
师:都是长、宽、面积,为什么一个是成反比例关系,一个成正比例关系?正比例和反比例有什么相同点和不同点?
生1:宽增加,长减少,乘积不变,所以长和宽成反比例关系。宽增加,面积也增加,它们的商一定,所以面积和宽成正比例关系。
生2:相同的是量都在发生变化,而且值都一样,不同的是一个量增加,另一个量减少,正比例同时增加或减少,且反比例的积一定,正比例的商一定。
设计意图:能找出正比例和反比例的异同点,正确区分正比例和反比例。从量的变化规律、图像的区别等入手,进一步深化对于两种比例关系的理解,并打通正比例和反比例之间的联系。
(四)融汇应用数形,内化模型思想
师:(出示图6)判断各题中两种量是否成比例关系。若成比例,成什么比例关系?

图6
师:回顾我们课堂中成反比例关系的两个量,你有什么想说的?
生:成反比例关系的两个量相乘的积一定相等。
师:对于反比例,你脑中留下了什么印象?
(生回答,如图6)
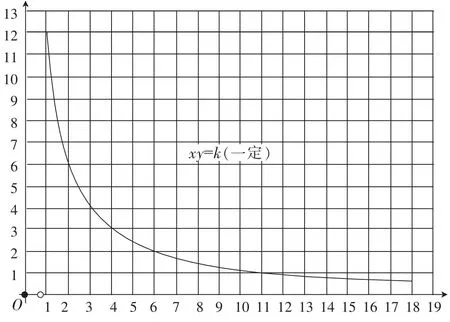
图6
设计意图:学生在同一情境中,紧抓两个量的变化规律,深入理解成反比例关系两个量的变化,已经了解了正比例和反比例以及不成比例之间的异同。在本次对比中,笔者发现学生会在脑中留下反比例的关系式和图像,这说明反比例的模型已经有了一定的建立。
