基于理想格的通用可组合两方口令认证密钥交换协议

2021-06-24王圣宝路凡义韩立东

电子与信息学报 2021年6期

舒琴王圣宝路凡义韩立东谭肖

(杭州师范大学信息科学与工程学院杭州 311121)

1 引言

两方口令认证密钥交换协议(Two-Party password-based Authenticated Key Exchange，2PAKE)能够使得协议参与者使用低熵、易于记忆的口令(password)协商生成一个高熵的会话密钥。

目前，大多传统基于数论的底层困难问题都存在量子解决算法[1，2]。因此，随着量子计算机的发展，基于这些难题构造的密码协议或方案正面临所谓的量子威胁。同时，应对量子威胁的所谓“后量子密码”研究方兴未艾。其中，基于格(lattice)上难题(简称格基)的2PAKE协议的研究成为热点之一。2009年，Katz等人[3]构造了首个格基2PAKE协议。该协议的安全性在基于不可区分的公共参考串(Common Reference String，CRS)模型[4]下得到证明。随后，Ding等人[5]和Zhang等人[6]各自构造出新的格基2PAKE协议，同样在CRS模型下证明了安全性。此后，又有多个格基2PAKE协议陆续被提出[7—9]，它们使用的安全模型皆为BPR模型[10]。

CRS模型与BPR模型没有考虑到协议的可组合性以及口令的相关性。相较而言，通用可组合(Universally Composable，UC)模型[11]则很好地解决了这些问题。2017年，Gao等人[12]基于SRP协议[13]，提出了一个格基扩展版本协议，称为RLWESRP。另外，RLWE-SRP采用了由Ding等人[14]所提出的误差调和机制。但是，该机制效率较低，使得协议双方提取出的共同比特只是具有高熵，而并非均匀分布，需要一个随机提取器来获得均匀的值。相比而言，Peikert[15]于2014年提出的改进误差调和机制能够使协议双方所提取的共同比特满足均匀分布。

采用Peikert式误差调和机制，本文提出一个更高效的具有通用可组合性的格基2PAKE协议，称为RLWE-CAPAKE，并在UC框架下证明其安全性。新协议的设计思想来源于Abdalla等人[16]于2008年提出的CAPAKE协议。新协议既保持了CAPAKE协议的优势，又能抵抗量子攻击。

2 预备知识

2.1 理想格

2.2 环上带误差学习问题

2010年，Lyubashevsky等人[17]提出了基于理想格的环上带误差学习(Ring Learning With Errors，RLWE)问题，并指出求解RLWE问题的难度可以量子规约到求解近似最短向量问题。被密码学界普遍认为能够抵抗量子攻击。

2.3 Peikert式误差调和机制

RLWE问题固有的误差问题会导致通信双方无法得到完全相同的会话密钥。为解决这一问题，Ding等人[14]在2012年首次提出误差调和机制(称为Ding式误差调和机制)。2014年，Peikert[15]指出Ding式误差调和机制中协议双方提取出的共同比特只是具有高熵，而并非均匀分布，需要一个随机提取器来获得均匀的值，这会带来较大的效率损失。他提出一个改进的误差调和机制(Peikert式误差调和机制)，该机制中协议双方提取的共同比特均匀分布。Peikert式误差调和机制具体描述如下：

2.4 安全模型

本文设计的协议的安全性在Canetti等人[11]提出的UC框架下，结合Canetti-Rabin[19]提出的具有联合状态的UC(Joint state UC，JUC)定理，使用UC混合模型证明。

3 基于理想格的两方PAKE协议

3.1 协议描述

相较于Abdalla等人[16]提出的CAPAKE协议，本文提出的新协议具有如下两个优势：(1)基于RLWE难题、采用文献[15]改进的误差调和机制，被密码学界普遍认为可以抵抗量子攻击；(2)新协议中，服务器不直接存储用户的口令，而只存储服务器ID及用户口令的哈希值HPW=H0(S||PW)。实际应用中，“单口令多用途”现象比较普遍，即用户往往针对许多不同的应用服务器使用相同的口令。该改进避免了当服务器沦陷后，敌手可直接获得用户口令，从而可向其他服务器冒充为用户的风险。

3.1.1 初始化阶段

用户加入系统时，需向服务器注册。用户 U 将其口令PW及服务器ID即S 输入哈希函数H0(·)计算得到HPW，同时从商群Rq中均匀随机选择公共参数a，将用户ID即U ， HPW及a通过安全信道发送给服务器 S。S 收到U 的注册信息后将〈U，HPW，a〉添加到存储在数据库中的列表 L上，本文设定外部敌手无法获得服务器内部信息。

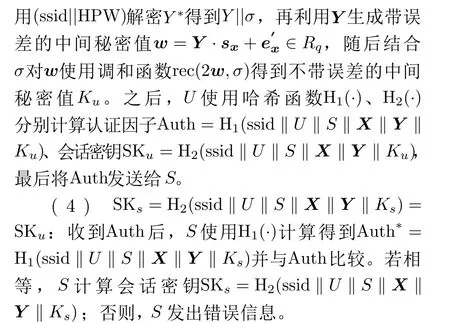
3.1.2 相互认证及密钥交换阶段

3.2 方案的正确性

图1 RLWE-CAPAKE的相互认证及密钥交换过程

4 安全性证明

(1)TestPwd查询：参与者完全被模拟时，验证某一方的口令是否为想要的那个口令；

(2)NewKey查询：参与者完全被模拟且口令未泄露时，验证两方是否拥有相同的口令；

(3)GoodPwd查询：参与者未完全被模拟时，验证某一方的口令是否为想要的那个口令；

(4)SamePwd查询：参与者未完全被模拟且口令未泄露时，验证两方是否拥有相同的口令。具体证明过程如下：

游戏 G0：该游戏是环境 Z与现实世界的敌手A及RLWE-CAPAKE协议的实例在随机预言模型以及理想密码模型下进行交互。

游戏 G1：理想攻击者S 模拟随机预言机和加解密预言机。

表1 UC框架不可区分性证明概览

引理 2 游戏 G1和游戏G 2对于任意环境 Z都是计算不可区分的。

引理 4 游戏G 3与游戏G 4对于任意环境 Z都是计算不可区分的。

5 效率分析

本节从安全性和计算与通信效率两方面对本文所提出的新协议与Ding等人[7]提出的PAK理想格扩展协议(RLWE-PAK)及Gao等人[12]提出的SRP理想格扩展协议(RLWE-SRP)进行比较。Ding式REC代表Ding式误差调和机制，Peikert式REC代表Peikert式误差调和机制。

如表2所示，这3个协议均基于RLWE问题，且通信开销也基本相同。RLWE-PAK与本文新协议的环运算次数基本相同，但是它的安全性证明基于BPR模型。如前所述，该模型相对UC模型而言不够完善。进一步，相比RLWE-SRP协议，虽然两者都在UC框架下被证明安全性，但是，本文新协议具有更少的环运算次数，即具有更高的计算效率。因此，综合而言，新协议具有更高的安全性和更好的效率。