基于分数低阶矩的干涉阵列米波雷达稳健测高方法

陈根华 陈伯孝 秦 永

①(南昌工程学院信息工程学院 南昌 310099)

②(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引言

波束宽、定位精度低的米波雷达是反隐身、反辐射导弹等防空系统的重要组成部分，如何提高米波(Very High Frequency， VHF)雷达的目标分辨力与定位精度一直是米波雷达的重要研究课题，尤其是低角目标的稳健测高。众所周知，当目标处于低仰角区时，宽波束照射目标时打地，产生强热杂波[1]，目标经由地(海)面反射的复杂多径信号，严重展宽单脉冲的差波束宽度，使得单脉冲测高时误差较大，甚至失效[2]。因此，限制米波雷达低角测高性能的关键因素是波束宽和复杂多径信号[3]。针对以上两大因素，目前国内外的大部分研究是利用超分辨法处理米波雷达波束宽的问题，比如合成导向矢量法、空域滤波法[4]等，也有研究复杂多径信号模型的随机扰动法[5]等。但参数化的测高算法严重依赖信号模型，其精确与否直接决定了算法的测高性能。而由Barton多径信号模型[2]可知，复杂多径信号可分为独立的镜面反射信号(specular component)和散射分量(diffuse component)两部分，其中非高斯(non-Gauss)分布的散射分量难以精确建模，工程应用时常将其简化为高斯白噪声，因此非高斯分布的散射分量是导致参数化低角测高算法非稳健的关键因素。另外，由阵列信号处理理论可知，增加阵列自由度(Degree Of Freedom，DOF)[6]可提高阵列分辨力，而为了降低计算量将面阵转换为线阵的行列合成技术却大大降低了测高算法的自由度，从而限制了米波雷达的测高精度与分辨力。

本文从以上两个关键因素出发，将InSAR中的干涉技术[7]应用到米波雷达，提出干涉阵列以扩展俯仰孔径，增加基线自由度，并将非高斯随机变量分析中的分数低阶矩理论[8]用于处理散射分量，提出了基于分数阶协变矩阵的干涉阵列米波雷达稳健测高方法。该方法先求解干涉阵列的分数阶协变矩阵，再结合干涉阵的双尺度移不变性和中心对称性，利用2维空间平滑法和双尺度酉ESPRIT算法[9]实现干涉阵列米波雷达稳健低角测高。另外，本文从理论上提出干涉阵列的3区基线设计法，将基线范围分为模糊区、高分辨区及非稳定临界区，为干涉阵设计提供理论指导。仿真结果验证了干涉阵列及测高算法的高精度及高分辨性能，也验证了3区基线设计法的正确性。

2 干涉阵列信号模型

由于米波雷达波长较长，工程上难以架设大孔径均匀矩形面阵(Uniform Rectangular Array，URA)阵列天线，因此本文提出如图1所示的倒T形干涉阵列，由子阵S1和S2组成，基线为 D，阵元间距分别为 dz和dy， S1为主收发阵列，S2仅为接收阵列，与S1以干涉形式扩展俯仰孔径，提高米波雷达测高自由度，而仅接收目标反射能量的S2也可用于提高目标发现概率。在方位上，较大孔径的S1可实现单脉冲精确跟踪，因为多径信号并不展宽单脉冲的方位差波束宽度[2]。本文主要研究低角目标的稳健测高，因此仅取S1中的S3与S2构成的干涉阵列，S3与S2孔径一致。

图1 干涉阵列米波雷达示意图

由Frauenhofer准则[2]可知，当反射面为复杂地(海)面时，多径信号中的散射分量呈现明显的非高斯特性[1]，其幅度与雷达工作频率、掠射角、遮挡效应等因素有关[2]。目前米波雷达低角测高算法常将多径散射分量忽略或简化为高斯白噪声，使其满足参数化的子空间类算法的应用条件，因此，模型失配是常规测高算法非稳健的关键因素。

3 基于分数低阶矩的干涉阵列米波雷达稳健测高算法

理论上，米波雷达低角测高是分辨同一仰角波束内的直达波与复杂多径信号，但根本问题为孔径与自由度，因此本文采用干涉阵列扩展俯仰孔径，增加基线自由度，以提高米波雷达低角测高性能。随着大规模计算能力快速发展，已可满足雷达高维实时计算需求。

针对非高斯分布的散射分量，从理论上证明非高斯随机变量的分数阶协变矩阵[8]与协方差矩阵一样都保留了阵列流形结构及秩亏性，因此先计算干涉阵列的协变矩阵，并再根据阵列中心对称性和双尺度移不变性将2维空间平滑法和双尺度酉ESPRIT算法[9]应用于分数阶协变矩阵，以实现复杂多径信号环境下米波雷达的稳健测高。

3.1 分数低阶矩(Fractional Lower Oder Moments，FLOM)及干涉阵列协变矩阵

协方差(covariance)是高斯分布的随机变量的最重要分析工具，而对于非高斯随机变量，其协方差无穷大，但其分数低阶矩是有界的[8]，因此可用分数低阶矩分析非高斯随机变量，分数低阶矩又称协变(covariation)。

由随机过程的期望的线性特征及相位旋转不变定理[11]，可得式(5)中右边第1项为

由协变系数定义可知，协变系数矩阵(CCM)与CM的关系可表示为

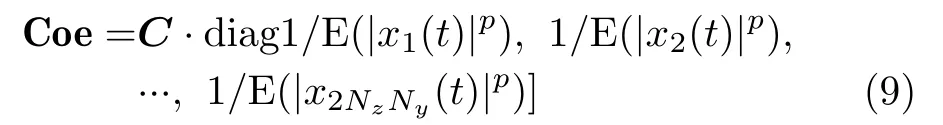
其中，diag(·)表示对角矩阵。

由式(8)、式(9)可知，CM和CCM不仅有效地处理了非高斯分布的散射分量野值点[1，8]，也类似于高斯白噪声背景下的阵列协方差矩阵，保留了阵列流形(manifold)信息，因此，常规的子空间类谱估计算法也可应用于分数阶协变矩阵，包括空间平滑解相干[9]、酉变换[5]、MUSIC等。工程上常用数值平均计算协变矩阵和协变系数矩阵Cˆoe，即

3.2 2维空间平滑解相干及实值化

本文拟采用ESPRIT算法[7]实现米波雷达稳健测高，而由式(8)可知，广义信号协变矩阵 Λ是秩亏的，需对CM进行解相干处理。常用的解相干处理方法有空间平滑法[9]、前后平均法[5]等。为了充分利用干涉阵的自由度和俯仰孔径，本文选用沿y轴平滑的2维空间平滑法实现解相干。

ˆEsˆEn

其中， 和 分别为信号和噪声子空间[9]。

3.3 双尺度酉ESPRIT算法

由双尺度ESPRIT算法[9]可知，由子阵内偏移量 dz的移不变性可得精度低但无模糊的方向余弦估计，称为粗估计；而由子阵间偏移量 D的移不变性可得精度高但周期模糊的方向余弦估计，称为精估计。因此，由酉ESPRIT算法[9]及自动配对算法得粗估计与精估计为

对方向余弦精估计解模糊后，结合多径信号特征，可得高精度无模糊的目标入射角为

4 干涉阵的3区基线设计法

总之，3区基线设计法说明了只有当基线处于高分辨区时，才能充分发挥干涉阵列的高分辨性能，而当基线处于模糊区和非稳定临界区，难以实现稳定的高分辨且易产生严重误差。因此设计干涉阵时需综合实际需求，选择处于高分辨基线区，使低角测高性能最优。

5 仿真实验

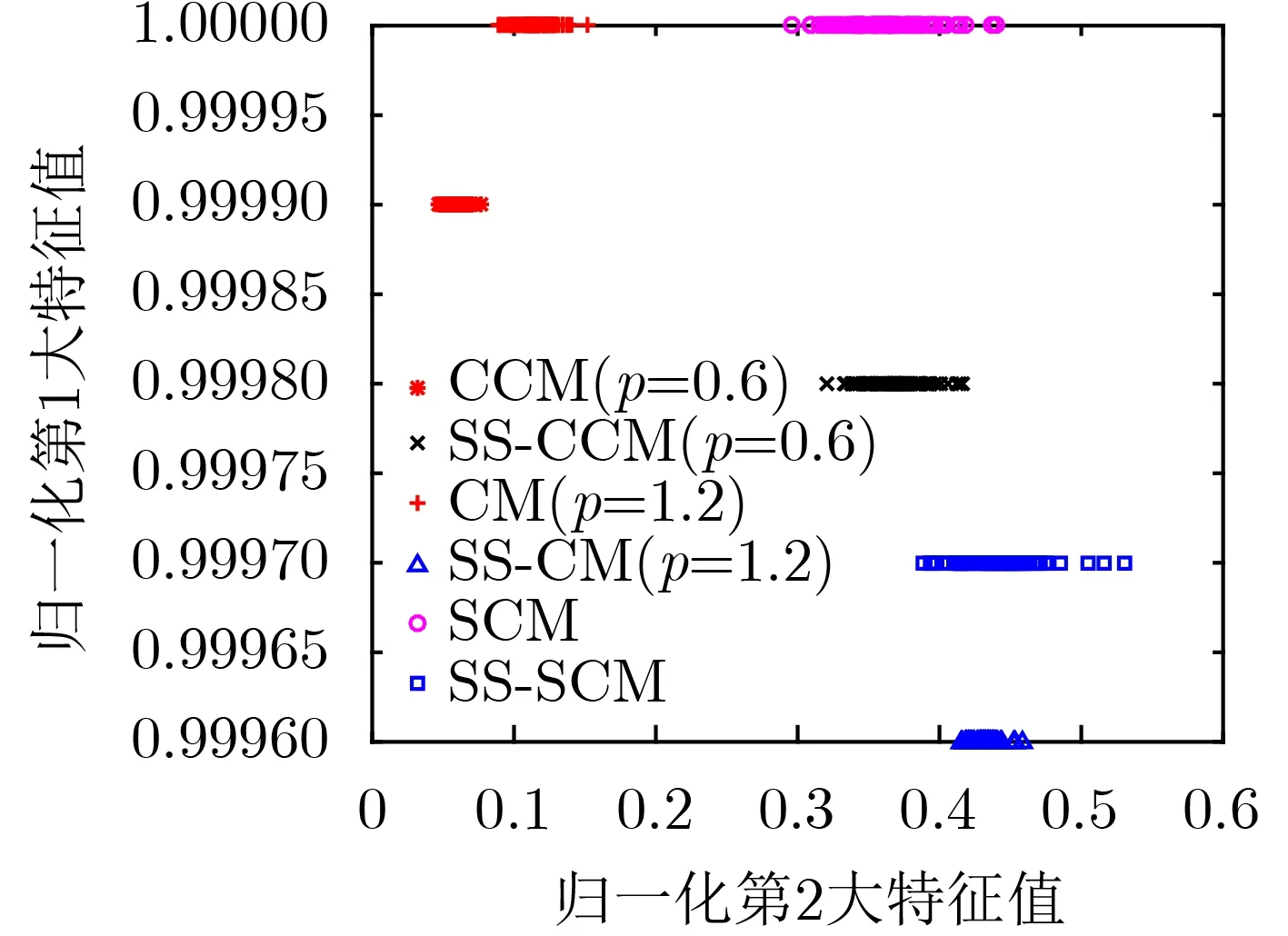
图2 分数阶协变矩阵特征值分布示意图

试验2 验证干涉阵列及本文低角目标测高算法的有效性。图3给出了不同基线下的低角目标测角的均方根误差(RMSE)，其中Nys=8。由图3可知，在低SNR时，基于分数低价矩的测高性能都明显优于常规SCM，且p=0.6时，基于CCM的测角精度约为SCM的5倍，充分说明了分数低阶矩处理非高斯分布的散射分量是有效的。图3也表明在高分辨区，D =20λ时测角精度比D =8λ时约提高了4倍，其中p=0.6时CCM的估计性能最佳，p=1.2时的CM次之。为验证干涉阵的有效性，本试验也比较了同等硬件规模的10× 16的URA， D =8λ和20λ时干涉阵的测高精度约为URA的4倍和6倍，且降低了SNR门限。本试验充分说明了分数低阶矩及干涉阵可实现米波雷达的高分辨稳健低角测高。

图3 不同分数低阶矩下干涉阵估计的精度

图4 平滑方向对估计性能影响

试验3 分析空间平滑方向及次数对测高算法性能的影响。图4给出了D =10λ时不同平滑方向和次数下的测高精度。沿方位维平滑时，利于SCM和CM；而沿俯仰维平滑时，CCM更优。由图4可知，CCM沿俯仰平滑较方位平滑后测高性能提高约3倍，因此，当对CCM解相干时，需沿俯仰方向，而CM和SCM需沿方位向平滑，以实现测高性能最优。

试验4 分析分数阶p对本文测高算法的性能影响。由图5可知，CM存在一个以p=0.8为中心，宽为0.2的 p门限窗，p 门限窗外都有稳定估计性能，对SNR不敏感；而CCM存在明显的p门限，低于门限时都能可靠分辨出低角目标，且p 门限随SNR增加而增大。因此本文试验计算CM和CCM时分别选择p=1.2和p=0.6。该试验说明需优化选择p值计算协变矩阵，以使测高算法性能最优。

图5 不同SNR下分数阶p 对测高性能的影响

试验5 分析ε混合噪声与分数阶p的关系。图6为不同ε下由CM和CCM得到的RMSE等高线图，仿真条件同试验1。从图可知，在CM时， p门限窗随ε不同而不同，且门限窗的中心与宽度随ε的增加而增大；而当p ＞1时，适用于任意ε混合噪声，因此，工程上应用时可选p ＞1。而在CCM时，ε 较大时p需选在2附近，而当ε ＜0.6时，需选取p ＜1。另外，本试验也说明基于CCM的测高性能要优于CM，为工程应用提供了理论指导。

试验6 验证3区基线设计法的有效性与正确性。图7(a)充分说明了3区基线设计法理论的正确性。当D =13λ和30λ时，子阵间波程差分别约为π和2 π，即分别位于非稳定临界区和模糊区，不能有效分辨低角目标，说明了长基线不一定能提高分辨力。只有处于高分辨区时才可实现干涉阵的高分辨力。图7(b)为典型3区基线下100次估计结果，其中D =20λ时处于基线高分辨区。由图可知在模糊区和非稳定临界区未能稳健分辨低角目标，而在高分辨区可稳定分辨目标，充分说明干涉阵的高分辨力。

图6 RMSE与ε 、p 的关系图

图7 3区基线设计法

6 结束语

针对复杂环境下米波雷达低角测高难题，本文从阵列孔径和多径信号散射分量的非高斯性出发，提出干涉阵列米波雷达结构，并从理论上验证分数协变矩阵保留了阵列流形特征，然后提出基于分数低阶矩的干涉阵列米波雷达低角稳健测高算法。实验结果证明干涉阵及测高算法的正确性与有效性，实现了复杂环境下低角目标的可靠分辨与测高，且基于CCM的测高性能要优于CM，应用时需选取最优的分数阶系数p。另外，设计干涉阵时需根据3区基线设计法，使其处于高分辨区，才能得到稳健的高分辨性能。