基于平行互质虚拟阵列的低复杂度二维DOA联合估计算法
2021-06-24余玉龙
李 林 余玉龙 韩 慧
①(电子信息系统复杂电磁环境效应国家重点实验室 洛阳 471003)
②(西安电子科技大学电子工程学院 西安 710071)
1 引言
波达角(Direction Of Arrival, DOA)估计是阵列信号处理中的一个重要研究课题,在无线通信、雷达和医学成像等许多领域中有广泛的应用。在阵列结构方面,平面阵的应用最为广泛。在过去的几十年中,国内外学者已经提出了许多基于平面阵列结构的DOA估计算法,包括面阵[1,2]、L型阵列[3]和平行线阵[4]等。平面阵列通常由几个均匀间隔的线性子阵列构成,具有有限的自由度,例如含 M个阵元的L型均匀线阵阵列,最多可以估计M -1个入射信号角度。
近年来,稀疏阵列由于能够有效提高阵列的自由度而受到广泛关注,例如最小冗余阵列[5]、嵌套阵列[6]和互质阵列[7]等。与传统阵列相比,稀疏阵列可以在保证性能的前提下充分地减少阵元数,或在阵元数相同的情况下,拥有更大的阵列孔径、更低的旁瓣级,通过对阵元位置和加权的解算改善测向算法的精度、分辨率和自由度。在稀疏嵌套阵列方面,文献[8]和文献[9]将嵌套阵列从1维DOA估计推广到2维DOA估计,提出了一种包含两个均匀间隔线性子阵的2维嵌套阵列。在L型互质阵列方面,有基于迭代最小化和离网格稀疏学习[10,11]。在平行互质阵列方面,文献[12]首次提出了利用平行互质阵列的互协方差矩阵构造1维向量,通过稀疏重构和最小二乘法得到相互匹配的DOA估计,提升了阵列的自由度,但是在小快拍情况下精度较差,且算法复杂度较高。文献[13]和文献[14]针对复杂度较高问题,将2维DOA估计问题转化为1维表示,利用互协方差矩阵和压缩感知方法进行角度估计,一定程度上提高了估计精度。上述算法主要利用了平行互质阵列的互协方差矩阵,文献[15]和文献[16]使用平行互质阵列的协方差矩阵,采用1维DOA估计结合功率进行匹配实现俯仰角和方位角估计,但是容易出现失配现象。
可以看出,现有平行互质阵列DOA估计算法只利用了阵列的协方差矩阵或互协方差矩阵,需要网格搜索和匹配,存在着计算复杂度较高、算法精度不足、容易出现失配等问题。针对现有算法的不足,本文提出了一种新的基于平行互质线阵2维DOA估计算法,利用两个线阵的协方差矩阵和互协方差矩阵构造新的DOA估计矩阵。在此基础上,利用SVD和ESPRIT算法,根据特征值和特征向量得到相匹配的方位角和俯仰角。与现有算法相比,本文算法充分地利用了自相关和互相关矩阵信息,可以估计更多的信源数,精度更高。同时由于阵元孔径的扩展,算法的分辨能力较高,计算复杂度较低,且在低信噪比和小快拍的情况下性能较好。
文中符号说明:(·)T, (·)*, (·)H, (·)-1和(·)+分别表示矩阵转置、共轭、共轭转置、求逆和求伪逆;diag(v)表示以v 为主对角线元素的对角矩阵;vec(·)表示矩阵拉伸;⊗ 表示Khatri-Rao积; I表示单位矩阵;arg(·)表示取相位角。
2 信号模型

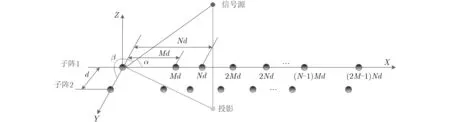
图1 平行互质阵列几何模型

3 基于平行互质虚拟阵列的低复杂度2维DOA估计算法
前文已指出,现有的2维DOA估计算法存在着计算复杂度较高、算法精度不足、容易出现失配等问题。针对这一问题,本文重点研究了2维虚拟阵列,提出了一种适用于平行互质虚拟阵列的2维DOA估计算法。
3.1 扩展矩阵构造


可见,矩阵 V1的尺寸为(MN +M)×(MN +M)。可以将V1表示为
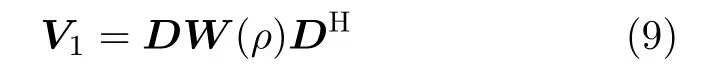
其中,W 为对角矩阵,和信号的功率相关。 D中包含了入射信号与X轴的夹角信息。
同样,可以通过接收的信号,定义子阵1和子阵2的互协方差矩阵为

同理,剔除v2中的重复元素,并取其中连续的虚拟阵元,可以得到

与式(7)类似,构造互协方差矩阵,即对 v¯2中的元素重新排列,可得
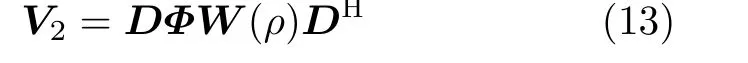
由式(8)和式(12),构造DOA估计的扩展矩阵

3.2 2维DOA估计
在3.1节中,通过子阵1的协方差矩阵及其与子阵2的互协方差矩阵,构造出DOA估计矩阵Rm。接下来,本文利用SVD和ESPRIT算法,由特征值和特征向量得到相匹配的方位角和俯仰角。
首先,对DOA估计矩阵Rm进行奇异值分解可得

其中,U1为信号子空间,U2为噪声子空间,则

其中,U11和U12的维度均为(MN +M)×K。
通过U11和U12的关系,构造矩阵 F,使得

通过对式(20)进行特征值分解,其对应的特征向量构成的矩阵为 T,通过(18)式有

通过联立式(21)和式(25),可得到相互匹配的方位角和俯仰角,即

3.3 算法步骤
基于以上理论分析,这里给出本文算法的具体步骤。
步骤 1 根据实际应用,通过有限的快拍数对协方差矩阵和互协方差矩阵进行估计,即

本文所提出的算法,利用互质虚拟阵列的思想,对于2维平行阵列进行扩展,能利用有限的阵元估计更多的入射角度,同时由于阵元孔径的扩展,对入射角度的分辨能力更好,并且在低信噪比和小快拍的情况下精确度相对较高,且算法复杂度更低。
4 实验仿真
在本节实验中,令 M=3, N=5,则子阵1的真实阵元数为2M -1+N,即L=10,阵元位置为{0 3 5 6 9 10 12 15 20 25}。考虑多个入射信号的情况,假设信号源个数K=11,即入射信号大于实际阵元数。此时,传统平行线阵算法均已失效,而本文算法仍然可以有效地估计出入射角度,如图2所示。本文提出算法能很好地扩展阵列孔径,提高阵元利用率,最多可估计MN +M -1个入射角度,远高于传统算法。
为了进一步验证提出算法的高分辨性能,我们假设入射信号个数为2,入射角为(10°,11°)和(11°,12°)。此时,传统算法失效。本文算法的实验结果如图3所示,可以看出,虽然存在一定误差,但依然可以分辨出两个非常接近的入射角度。需要注意的是,由于角度较为接近,实验中需要较高的信噪比和快拍数。
为了衡量算法的估计精度,本文采用均方根误差(RMSE)准则,定义为

图4为快拍数对本文算法性能的影响,并与已有算法进行比较。其中,文献[4]基于平行线阵2维PM算法,文献[12]基于基于平行互质阵列算法。考虑现有算法的适用范围,这里对4个信源进行估计,入射角分别为(10°,10°) , (20°,20°),(30°,30°)和(40°,40°)。可以看出,本文算法在少量快拍下也有较好的估计性能。特别当快拍数P=10时候,本文算法依然可以实现有效DOA估计,可适用于小快拍场景下工作。
接下来,分析信噪比变化对图4中各种算法性能的影响。为了减小快拍数对不同算法的影响,实验中采用较大的快拍数,即P=1000。实验中入射信号情况与图4相同,实验结果如图5所示。可以看出,本文算法在低信噪比情况下依然具有较高的估计精度。

图2 K=11时算法估计结果(SNR=10 dB, P=500)
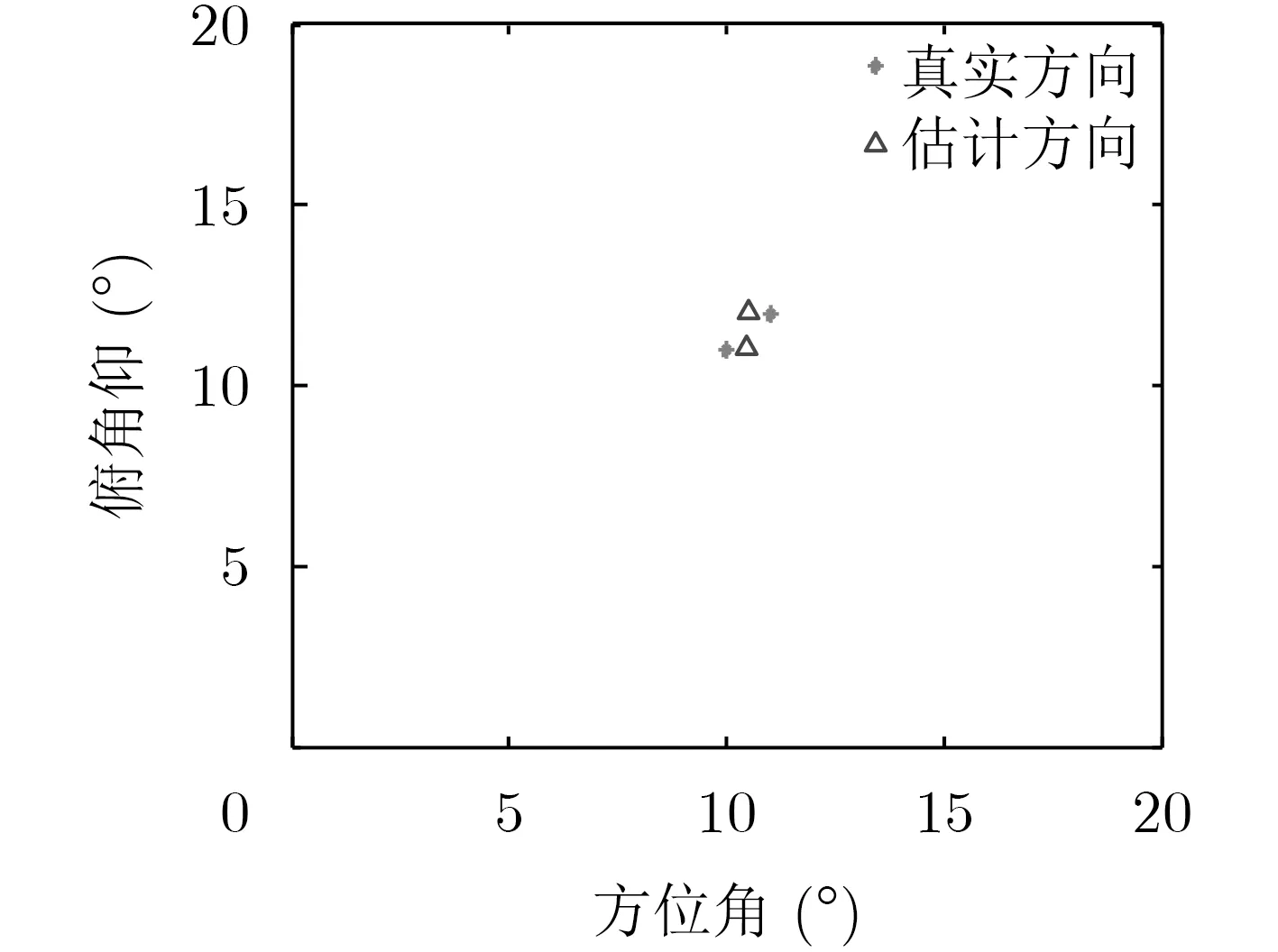
图3 高分辨率实验(K=2, SNR=20 dB, P=500)
最后,为了对不同DOA估计算法的复杂度进行比较分析,在相同硬件和软件条件下,进行1000次蒙特卡罗实验,统计各种算法的运行时间。实验中计算机的CPU为I7-8550U,内存为8 G。实验中入射信号情况与图3和图4相同,采样快拍数P =500,信噪比SNR=20 dB。实验统计结果如表1所示,可以看出,本文算法的计算复杂度优于文献[12]中的平行互质阵列算法,但略高于平行线阵PM算法。
5 结论
本文提出一种基于平行互质虚拟阵列的低复杂度2维DOA估计算法,将传统平行线阵与互质虚拟阵列相结合。本文采用扩展的DOA矩阵,在进行DOA估计时,通过奇异值分解并提取旋转不变因子,避免了传统算法的谱峰搜索,降低了算法复杂度,获得了自动匹配的DOA估计。同时,采用虚拟阵列扩展了阵元孔径,解决了传统DOA估计算法入射信源数小于真实物理阵元数问题。仿真实验结果表明,本文所提算法具有更高的分辨能力,可以分辨更多的辐射源信号,而且在低信噪比和小快拍情况下也优于传统DOA估计算法。
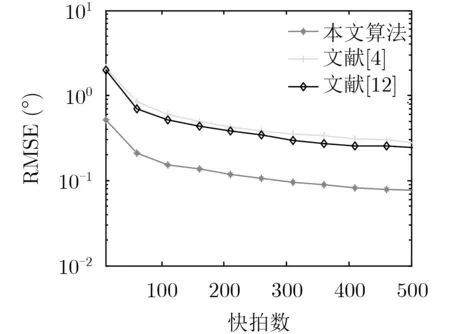
图4 不同快拍数算法性能对比(K=4, SNR=10 dB)
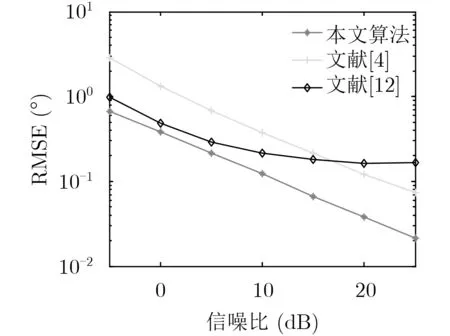
图5 不同信噪比下的性能分析(K=4, P=1000)

表1 不同2维DOA估计算法运行时间(s)
