部分相干Airy涡旋光束在非Kolmogorov谱中的模态强度
2021-06-24高金全周正兰徐华锋
高金全,周正兰,徐华锋, 吴 彬,屈 军
(安徽师范大学 物理与电子信息学院,芜湖 241002)
引 言
随着通信行业的快速发展,社会对通信速率的要求越来越高,传统的无线电通信不能满足用户的需求。为了弥补数据共享时代数据传输的压力,近些年来,自由空间光通信(free space optical communication, FSO)成为研究的热点,光作为信息传输的载体,具有非常高的可用光带宽,能够实现两个定点间的高速率传输,并且传输距离可达数千米[1-3]。研究发现,光不仅有自旋角动量,而且涡旋光束中每个光子都携带轨道角动量(orbital angular momentum, OAM)[4],轨道角动量可作为信息传输的载体。涡旋光束具有特殊的相位结构和确定的轨道角动量,在无线光通信领域备受关注[5-7]。由于不同模态的OAM光束相互正交,理论上它的拓扑荷数可以是无限的,构成无穷维希尔伯特空间,具有极高的自由度。因此可以在不增加频谱带宽的情况下,提高信号通道的编码容量[8-9]。同时OAM的拓扑荷和方位角之间的不确定关系,有利于提高OAM承载信息的安全性[10]。涡旋光束在光通信方面展现了巨大的潜力[11-12],WANG等人通过使用携带轨道角动量的正交的Laguerre-Gaussian模进行四模多路复用和解复用的方法,实现了12.8bit/s/Hz的高频谱效率;BOZINOVIC等人证明了利用光的轨道角动量创建在单个光纤中多路复用且正交,空间上不同的数据传输通道流的可行性,在光纤中采用10个波长的两种OAM模式的同时复用,获得了1.6Tbit/s的传输速率,结果表明,OAM可以为未来光纤网络中的数据复用提供额外的自由度。
大气湍流严重影响了OAM在实际自由空间光通信中的应用[13-14]。大气的温度和压力的不均性会导致折射率沿传输路径随机变化,从而使OAM光束的相位产生畸变,导致光束的光强闪烁,破坏OAM态的正交性,引起不同OAM态的信道之间的模态串扰,初始的OAM态将被破坏并扩散到邻近态,使轨道角动量携带的信息丢失[15]。传统的Kolmogorov湍流模型,被广泛用于光束在大气湍流中的传播,并且取得了大量的研究成果[16-17]。随着湍流测量技术的发展,研究发现大气湍流与Kolmogorov湍流模型的结构存在着差异,Kolmogorov湍流实际上是非Kolmogorov湍流的一个特例。为了得到更准确的实际大气信道传输结果,降低湍流对光束的影响,国内外学者开展了对涡旋光束在非Kolmogorov湍流中的传输特性的研究[18-20]。ZHANG等人研究了单光子在倾斜的非Kolmogorov湍流通道中的轨道角动量串扰,结果表明,轨道角动量的串扰概率随着湍流强度、方位角模态指数、轨道角动量量子数的增大而增大。OU等人研究了Bessel-Gaussian光束的螺旋谱在非Kolmogorov湍流中的扩散,发现基于OAM的通信系统的信道容量和螺旋谱随着湍流幂指数变化的趋势一致。TANG等人研究了部分相干Lommel光束在非Kolmogorov湍流中的传输特性,结果发现,部分相干Lommel光束的相干宽度在传输过程中决定了模态强度。
Airy光束具有无衍射、自愈合和自加速的特性,学者们开展了大量有关它的产生、传播和应用等方面的研究[21-22]。PU等人基于He-Ne激光器光源以及加载相位信息的反射式空间光调制器,从实验上产生了部分相干Airy光束。KE等人从理论上研究了部分相干Airy光束在大气湍流中的光束扩展与漂移。为了了解Airy光束在大气湍流中抗干扰的能力,本文中推导了非Kolmogorov湍流大气中部分相干Airy涡旋光束的模式概率密度(model probability density, MPD)和串扰概率密度(crosstalk probability density, CPD)的表达式。在此基础上,数值模拟了非Kolmogorov湍流大气中部分相干Airy涡旋光束的螺旋谱分布以及MPD和CPD受湍流参量和波数参量的影响,从而获得该光束在自由空间光通信中的最优参量。
1 理论推导
在柱坐标系和近轴近似下,Airy涡旋光束的电场解析表达式为[23-24]:
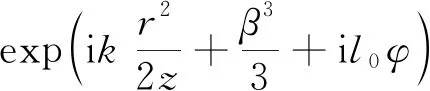
(1)
式中,柱坐标(r,φ,z)分别表示光束的径向位置、角向位置和传输距离;k=2π/λ是波数,λ为波长;w0与主Airy波瓣的宽度有关,r0表示主亮环的半径,β为截断指数,l0是OAM的拓扑荷数;Jl0()表示阶数为l0的第1类贝塞尔函数。
基于拓展的惠更斯-菲涅耳原理,当传输距离为z时,部分相干Airy涡旋光束的交叉谱密度函数可以表示为[25-26]:
〈exp[ψ(ρ1′,ρ1)+ψ*(ρ2′,ρ2)]〉d2ρ1′d2ρ2′
(2)
式中,ρ1≈(r,φ)和ρ2≈(r′,φ′)为两个位于输出面的任意横向位置矢量,ρ1′和ρ2′为两个位于源平面的任意横向位置矢量;W(ρ1′,ρ2′,0)是部分相干Airy涡旋光束在源平面的交叉谱密度函数;〈〉为系综平均,*表示复共轭,ψ表示球面波在湍流中由源平面传输到输出面时复相位的随机项。
利用Rytov近似,部分相干Airy涡旋光束在输出面的交叉谱密度函数可以表示为[27]:
W(ρ1,ρ2,z)≈E0(ρ1,z)E0*(ρ2,z)μ(ρ1,ρ2)×
〈exp[ψ(ρ1,z)+ψ(ρ2,z)]〉
(3)
式中,μ(ρ1,ρ2)是光谱的相干度,它的高斯形式可以表示为[28]:
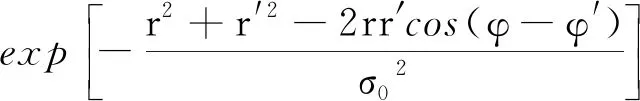
(4)
式中,σ0是光束源的空间相干宽度。
(3)式最后一项为大气湍流引起的相位波动,可以表示为[29]:
〈exp[ψ(ρ1,z)+ψ(ρ2,z)]〉=

(5)
式中,0阶贝塞尔函数J0可以近似为[30]:

(6)
式中,κ为2维空间频率;Φn(κ,α)是湍流介质的折射率起伏有效功率谱函数;ξ是归一化距离变量,ξ=1-z/L,L为沿z轴从发射机的发射孔到接收机的传输距离。
根据非Kolmogorov湍流理论,受湍流的内外尺度效应的影响,湍流有效功率谱可以表示为:

(7)
式中,α是湍流谱幂指数,Cn2是单位为m3-α的湍流折射率起伏结构常数。

(8)
式中,Γ()为伽马函数。

(9)
式中,κn=c(α)/n0,κm=8π/m0分别表示湍流涡流内尺度和外尺度对应的空间频率,n0和m0分别为湍流内尺度和外尺度。

(10)

参量ηx,ηy可以表示为[31]:

(11)
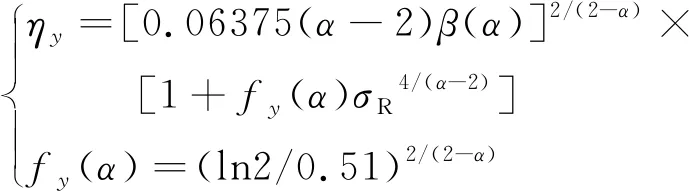
(12)

(13)
基于Rytov相位结构函数的二次项近似,(5)式可以表示为[32]:
〈exp|ψ(r,φ,z)+ψ*(r′,φ′,z)|〉≈
exp{-[r2+r′2-2rr′cos(φ-φ′)]/ρ02}
(14)
式中,ρ0为球面波在非Kolmogorov湍流中的空间相干长度,形式可以表示为:

(15)
当部分相干Airy涡旋光束在大气湍流中传播时,受到大气折射率起伏变化的影响,湍流引起的累积效应假定为OAM光束的相位扰动,导致涡旋模式偏离了OAM的原始本征态。携带轨道角动量的部分相干Airy涡旋光束的复振幅表达式为:
E(r,φ,z)=E0(r,φ,z)exp[ψ(r,φ,z)]
(16)
为了获得新的涡旋模式分量的权值,将部分相干Airy涡旋光束分解为携带相位因子exp(ilφ)螺旋谐波的叠加[33]:

(17)
式中,l是基于螺旋谱理论分解后的拓扑荷数。
展开系数:
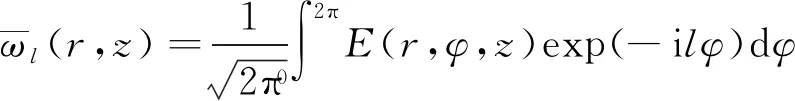
(18)

E0*(r′,φ′,z)μ(r,φ)μ′(r,φ′)×
〈exp|ψ(r,φ,z)+ψ*(r′,φ′,z)|〉×
exp[-il(φ-φ′)]dφdφ′
(19)
结合(1)式、(4)式、(14)式,部分相干Airy涡旋光束在非Kolmogorov湍流中传播的模式强度概率密度的表达式:
Jl0(kr0r′/z)exp(-ikr′2/(2z)+β3/3-il0φ′)×
exp{-[r2+r′2-2rr′cos(φ-φ′)]/σ02}×
exp{-[r2+r′2-2rr′cos(φ-φ′)]/ρ02}×
exp[-il(φ-φ′)]dφdφ′
(20)
根据积分表达式:

2πexp(-ilφ′)Il(ξ)
(21)
可得:

1/ρ02)(2r2)]Il-l0[(1/σ02+1/ρ02)(2r2)]
(22)
式中,Il和Il-l0分别表示阶数为l和l-l0的第1类修正贝塞尔函数。假设l-l0=Δl,则(22)式可写成:

1/ρ02)(2r2)]IΔl[(1/σ02+1/ρ02)(2r2)]
(23)
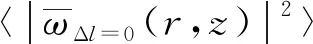
对于直径为D的有限孔径接收机,涡旋模式的螺旋频谱分布可以表示为:

(24)
2 数值计算与分析
根据部分相干Airy涡旋光束的涡旋模式的螺旋频谱分布公式(24)式,采用数值模拟方法对不同光束参量和湍流条件下的螺旋谱分布、模式概率密度和串扰概率密度进行了分析。除非另有规定,否则仿真中使用的参量设置为:λ=1550nm,w0=0.01m,r0=0.001m,β=0.05,α=3.67,σ0=0.03m,n0=0.001m,m0=1m,D=0.02m,l0=1,z=1km,Cn2=10-13m3-α,Δl=1。
在由弱到强的非Kolmogorov湍流中,不同相干宽度的Airy涡旋光束的螺旋谱分布如图1所示。反映了湍流造成能量从初始OAM本征态向其它本征态迁移。当湍流较弱时,串扰主要发生在相邻模式之间,相对于强湍流而言可以忽略不计,在强湍流条件下,串扰强度迅速增加,并且向更多边缘模态传播,造成误比特率显著提高。通过纵向对比发现,随着相干宽度的增加,模式概率逐渐增加,串扰概率逐渐减小,空间相干宽度对部分相干Airy涡旋光束的模态强度变化有较大的影响。理论上部分相干Airy涡旋光束受湍流的影响要小于完全相干Airy涡旋光束,但是当相干宽度较小时,相干性较差的部分相干Airy涡旋光束在非Kolmogorov湍流中传播时会更加容易丢失信号通道中的信息,选择合适的相干宽度将有利于部分相干Airy涡旋光束在非Kolmogorov湍流中的传播。
从图2a可以看出,随着传播距离的增加,串扰概率密度逐渐增加并趋于稳定值,Δl越小,串扰概率密度增长得越快,这是因为在强湍流中,串扰对邻近模态的影响较大,并逐渐扩散至其它模态。另外也反映了能量集中在光束的中心,所以靠近主瓣的旁瓣的能量高于其它旁瓣。在图2b和图2c中,当z增大,MPD呈急剧下降的趋势,最终达到稳定状态;CPD迅速上升,达到最大值后有一个下降的过程并趋于稳定。拓扑荷数越大,受湍流影响也越大,拓扑荷数相对于其它因数对模态强度影响较小,可以忽略不计。
图3主要反映了接收机的直径对部分相干Airy涡旋光束的MPD和CPD的影响。从图中可以直接看出,光束沿着z方向传播时,随着接收机的直径的增大,MPD下降得越快,相对的,CPD上升得也越快,在达到最大值后趋于平稳。选取合适的接收机的直径可以有效地减弱湍流的影响,提高光束的传输性能,当接收机的直径较大时,只适合短距离的传播。

Fig.1 The spiral spectrum distribution of partially coherent Airy vortex beam

Fig.2 a—CPD of partially coherent Airy vortex beam with different Δl b,c—MPD and CPD of partially coherent Airy vortex beam with different l0
由图4可见,随着传播距离的增加,部分相干Airy涡旋光束在弱湍流中相对于强湍流而言,MPD下降得较为缓慢,CPD单调增加,这是由于强湍流引起的累积效应迅速增加造成的。在远场中,强湍流下的MPD逐渐平稳,CPD也相对的平缓并有减小的趋势,造成这种现象是因为高阶串扰的增强减小了Δl=1时CPD的权重。提高MPD以增强OAM多路复用通信的性能并减轻湍流的影响,这对长距离传输具有积极作用。
在图5中,相干性较好的部分相干Airy涡旋光束的MPD下降得比较快,相干性差的部分相干Airy涡旋光束的MPD下降趋势较平缓,这是因为相干性差会导致部分相干Airy涡旋光束的初始模态强度严重色散,从而抑制了能量向边缘扩散。相干性较好的部分相干Airy涡旋光束的CPD迅速增加,在达到最大值后有一个减小的趋势,相干性差的部分相干Airy涡旋光束的CPD只有略微上升便开始下降,这说明选择合适的空间相干宽度对部分相干Airy涡旋光束的传输性能的提高至关重要。

Fig.3 MPD and CPD of partially coherent Airy vortex beam with different size of the receiving aperture D
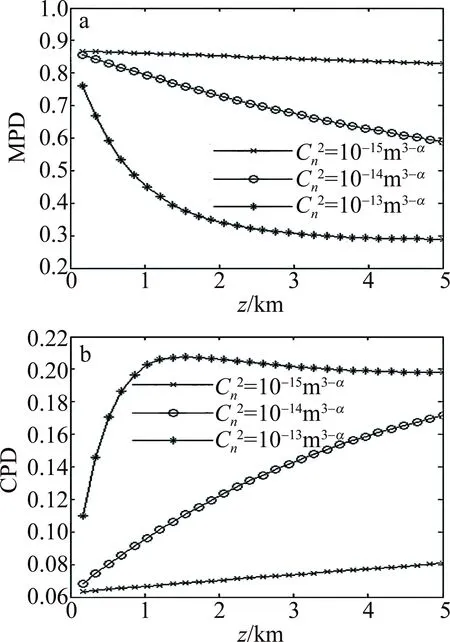
Fig.4 MPD and CPD of partially coherent Airy vortex beam with different turbulence strength
图6中分析了光束波长对部分相干Airy涡旋光束的MPD和CPD的影响。随着湍流的增强,各个波长的部分相干Airy涡旋光束的MPD都呈下降的趋势,其中长波长的光束比短波长的光束下降得更加缓慢。相对的,短波长的部分相干Airy涡旋光束的CPD在由弱到强的湍流中迅速上升并达到最大值,随着湍流逐渐变强,又开始平缓下降,这是高阶串扰的增强所导致的。长波长的部分相干Airy涡旋光束的CPD逐渐增加并最终保持稳定,这说明长波长的部分相干Airy涡旋光束对湍流的敏感性较低,受影响的概率更小,更加适合在大气湍流中传播。
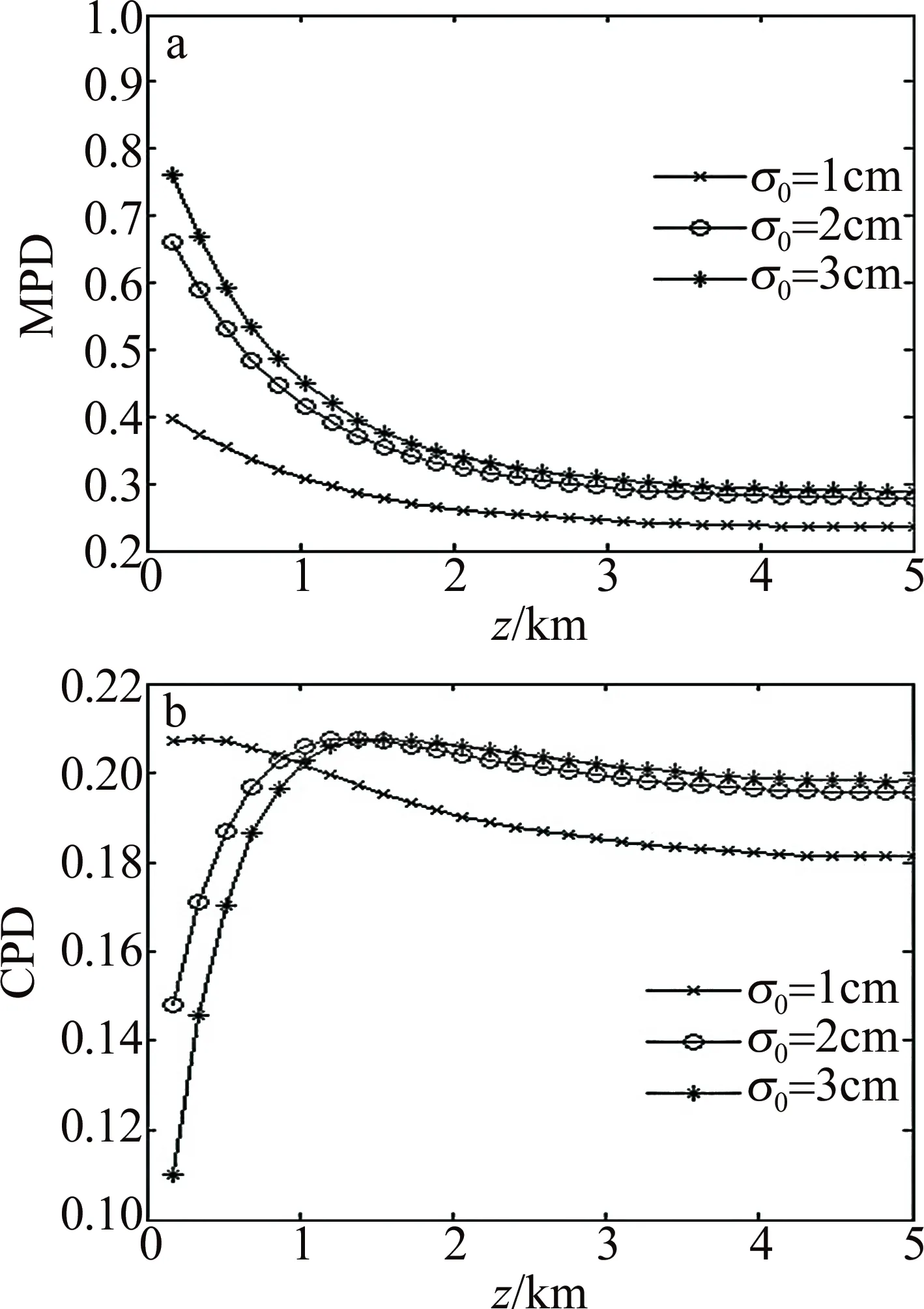
Fig.5 MPD and CPD of partially coherent Airy vortex beam with different spatial coherence width

Fig.6 MPD and CPD of partially coherent Airy vortex beam with different wavelength
从图7中可以看出,随着湍流强度的增大,α越大,部分相干Airy涡旋光束的MPD下降得越少。这是因为α直接影响了湍流中的旋涡数量,α越大,旋涡越少,光束的闪烁效应越弱。同时,α越小,部分相干Airy涡旋光束的CPD随着湍流强度的增大迅速上升至最大值又快速下降,这说明湍流的折射率起伏较大,严重影响了部分相干Airy涡旋光束的通信性能,合适的α有利于减小串扰,提高传输质量。
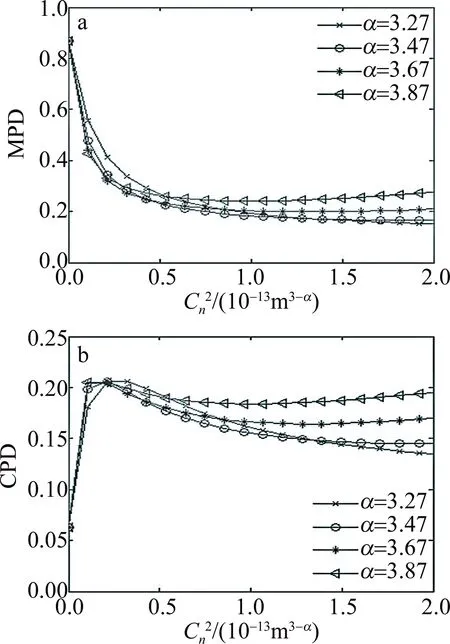
Fig.7 MPD and CPD of partially coherent Airy vortex beam with different values of non-Kolmogorov spectrum parameter
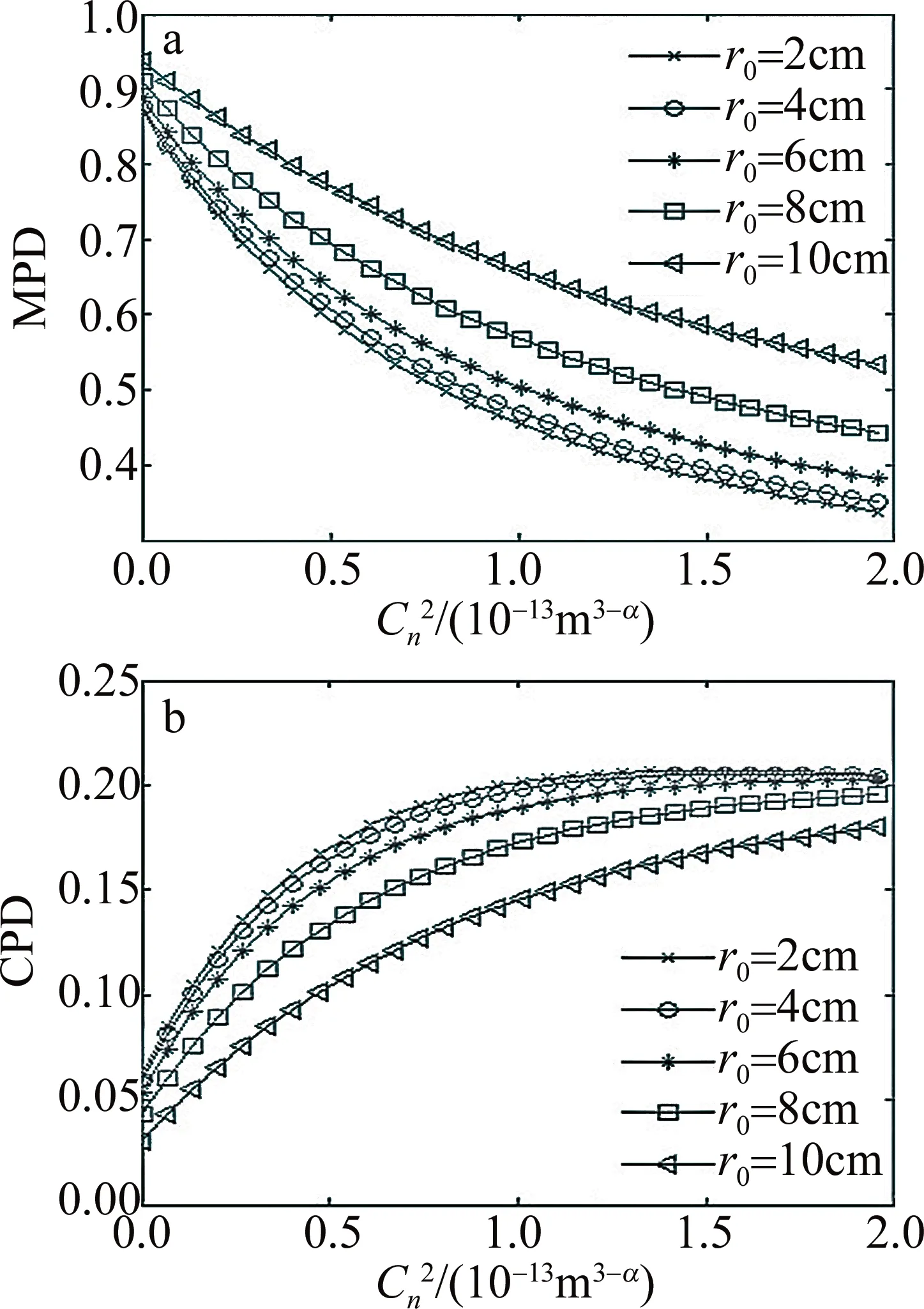
Fig.8 MPD and CPD of partially coherent Airy vortex beam with different main ring radius
图8表明,随着湍流强度的增加,部分相干Airy涡旋光束的主亮环半径越大,MPD下降得越缓慢,相对的,部分相干Airy涡旋光束的主亮环半径越小,CPD上升得越快,并在达到峰值后有略微下降。在强湍流中,不同主亮环半径的部分相干Airy涡旋光束的CPD基本一致。通过比较发现,主亮环半径较大的部分相干Airy涡旋光束在非Kolmogorov湍流中传播的性能更好。
3 结 论
分析了携带轨道角动量的部分相干Airy涡旋光束在非Kolmogorov大气湍流中传播时,光束参量和湍流参量对轨道角动量模的模式概率密度(MPD)和串扰概率密度(CPD)的影响。不仅考虑了源光源的相干性、拓扑荷数、波长和主亮环半径与轨道角动量模式之间的密切联系,还讨论了湍流强度、湍流谱幂指数和接收机直径对传输性能的影响。研究表明,拓扑荷数越大,抗干扰能力越弱;长波长的部分相干Airy涡旋光束的模态强度受湍流的影响较小;主亮环半径较大的部分相干Airy涡旋光束更适合在湍流中传播;接收机的直径越大,MPD越小,当接收机直径到达一定值时,对轨道角动量的串扰影响较小,上述结果与参考文献[23]及参考文献[24]中的结论相一致。此外,空间相干宽度决定了部分相干Airy涡旋光束模态强度的色散;轨道角动量的串扰随着湍流强度的增强而增大;较大的湍流幂指数有助于减小CPD。本文中得到的理论结果对OAM在空间光通信中的应用具有一定的参考价值。
