斜齿轮系统动力学行为研究

张 伦，吕小红，高 博

（1.兰州交通大学机电工程学院，兰州 730070；2.甘肃省轨道交通装备系统动力学与可靠性重点实验室，兰州 730070；3.兰州长信机车配件有限公司，兰州 730070）

0 引言

齿轮系统现如今被广泛运用于机械、航空、船舶等行业。因为其是机器中最主要的运动及动力传递装置，其动态性能的好坏会直接影响整个机器的运行状态［1］。有些学者已经对冲击碰撞系统的周期运动行为进行了大量研究，这类研究方法同样适用于斜齿轮振动系统中［2-3］。苏程等［4］研究了不同侧隙值下，啮合阻尼比对单级齿轮传动的影响；刘大亮等［5］在考虑齿侧间隙对齿轮动态特性影响的同时，还考虑了轴承间隙对整个系统的影响；田亚平等［6］采用数学理论推导与数值分析相结合的方法，对齿轮与转子耦合系统进行了仿真研究。还有一些文献对故障齿轮系统进行了动力学行为研究［7-9］。

本文主要建立斜齿轮模型，兼顾考虑齿侧间隙和轴承间隙，绘制分岔图与相轨迹图来揭示其动力学行为，为此系统设计安全性和平稳性提供理论依据，并且结合工程应用实际，模拟斜齿轮系统轻微磨损状态，进行了磨损状态的动力学行为探究。

1 模型建立

图1所示为一种斜齿轮传动动力学模型。假设：（1）齿轮和轴均为刚性元件，不考虑轴和轴承的质量；（2）齿轮为对称安装，不存在偏心，并且将安装的误差计入齿轮的综合传动误差；（3）整个支撑系统和啮合副简化为阻尼元件和刚度元件，齿轮1为左旋齿轮，齿轮2为右旋齿轮，压力角α=20°，螺旋角β=18°，模数m=0.003，齿数比为35∶67。

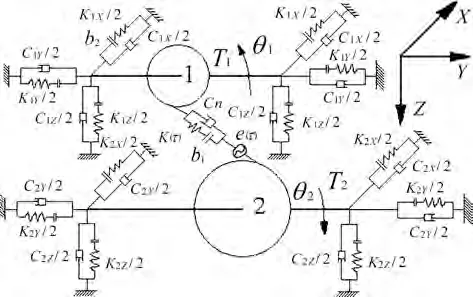
图1 斜齿轮动力学模型

振动和误差导致斜齿轮副沿啮合点法线方向的相对微位移为：

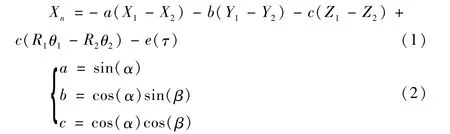
斜齿轮副沿法线方向的啮合力及各个坐标轴方向的分力分别为：

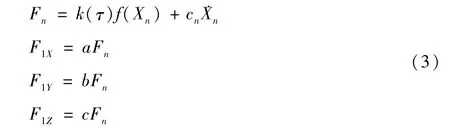
式中：R1、R2分别为齿轮1和齿轮2的基圆半径；θ1、θ2分别为齿轮1和2的旋转角位移；e（τ）为斜齿轮副的时变综合误差函数；k（τ）为时变啮合刚度；cn为啮合阻尼；F1X、F1Y、F1Z分别为齿轮1所受的径向力、轴向力和切向力。

齿轮副时变啮合刚度可表示为：

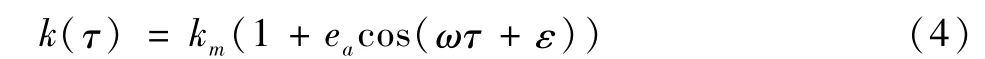
式中：km为齿轮副的平均啮合刚度；ea为无量纲刚度幅值；ω为无量纲啮合频率；ε为初相位。

时变综合误差函数可表示为：

采用集中质量法建立运动微分方程如下：

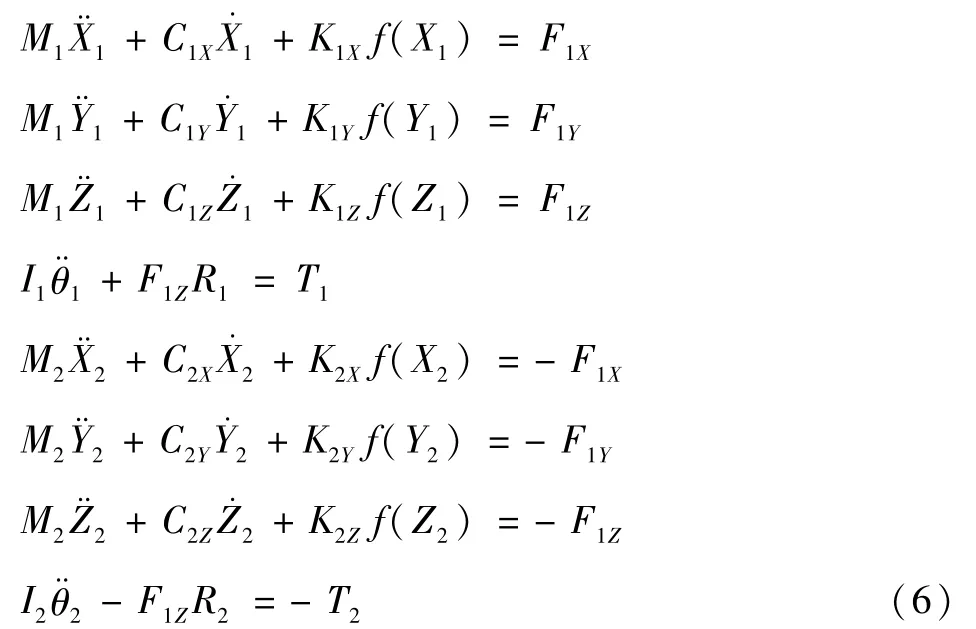
式中：Mi为齿轮i的质量；Ri为齿轮i的基圆半径；Xi、Yi、Zi为齿轮i沿X、Y、Z坐标轴方向的微位移（其中X¨i，X·

i为齿轮i沿X轴方向微位移的二阶和一阶导数；Y、Z方向同理，不赘述）；θi为旋转角位移；Cij，Kij为支撑阻尼和支撑刚度；T1，T2分别为输入和输出转矩；i=1，2；j=X，Y，Z。

引入无量纲参数：

xi=Xi/bc，yi=Yi/bc，zi=Zi/bc，t=ωnτ，特征频率ωn=为齿轮啮合副的当量质量；其中mi=为齿轮i当量质量。则有无量纲运动微分方程：

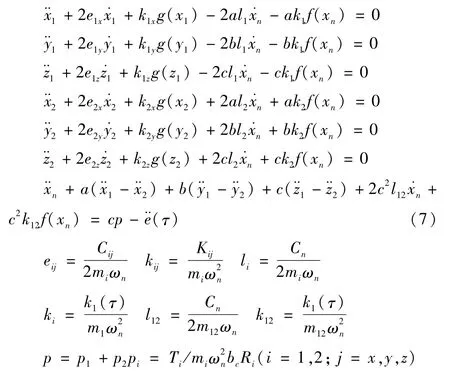
f（xn）和g（x1）分别为齿侧间隙函数和齿轮1在x方向上的支撑间隙函数。均可表示为：

2 动力学行为研究

斜齿轮系统是受周期激励的系统，其激励周期为T=2π/ω，θ=ωt，因此取Poincaré截面为：

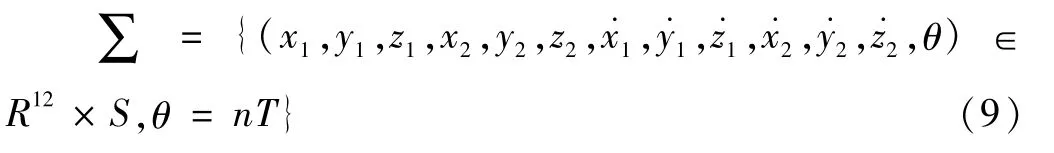
2.1 啮合阻尼比对系统分岔特性的影响

根据无量纲运动微分方程，取系统的基准参数如下：特征尺寸bc=30×10-6，特征频率ωn=23 414，无量纲齿侧间隙b=1，无量纲输入载荷p1=0.048，选取无量纲啮合频率区域ω∈［0.2，3.0］，对系统进行数值分析，得到如图2所示不同啮合阻尼比下的系统运动分岔图。通过图2（a）可知，在啮合阻尼比ξ=0.01条件下，当啮合频率ω＞2.45时，系统处于稳定的周期1运动状态。随着ω的递减，当ω穿越2.45时，系统经倍化分岔进入短暂周期2运动状态。ω继续递减，在ω∈［1.45，2.29］范围内，系统呈现出大幅的混沌区域，此时系统运动极不稳定，并且在ω∈［1.94，2.15］范围内，夹杂着短暂的周期3运动状态。而在ω∈［1.24，1.45］的区间内，如图2（b）所示，系统的运动状态经历了周期8—混沌—周期4—周期2的变化过程，大体呈现出逆倍化分岔的形式。而后系统又经历了混沌—周期2—周期1—混沌—周期1等运动状态，并且在跨越ω=0.536时，经跳跃分岔转迁为稳定的周期1运动，此时系统恢复稳定。

当ξ增加至0.03时，系统分岔图如图2（c）所示。与ξ=0.01时相比较而言，混沌区域略微减少，周期运动区域有所增加。具体运动形式表现如下：当ω＞2.266时，随着啮合频率ω的递减，系统经由周期1—周期2—周期4倍周期序列分岔进入混沌。随着控制参数继续递减，系统经历了一片混沌区域，在跨越ω=1.981时，系统的拓扑结构发生改变，由混沌运动退化为稳定的周期24运动。接着经由一系列的逆倍化分岔过程：周期24—周期12—周期6—周期3，在ω=1.70时结束周期3运动，并且在啮合频率ω∈［1.53，1.70］时系统再次失去稳定性，表现为混沌运动状态，而在此区域内还包含着极短暂的周期2运动。当ω＜1.53后，系统的运动状态经历了周期8—周期4—周期2—周期1—（跳跃分岔）—周期1的变化过程。

继续增加啮合阻尼比ξ的值，取ξ=0.05，系统分岔图如图2（d）所示。此时系统的运动形式变化比较简单，不存在离散的混沌区域，运动形式与ξ=0.03时大致相似。随着啮合频率ω递减，系统同样经历了周期1—周期2—周期4的倍化分岔过程，在ω=2.2时，系统失去稳定性进入混沌运动。与ξ=0.03所异的是，此时的混沌运动是一片连续的区域，不存在混沌—逆倍化分岔—混沌的变化过程。ω继续递减至1.65时，系统结束混沌运动，回归到稳定的周期8运动状态，并且经历一系列逆倍化分岔，最终变为稳定的周期1运动状态。图3所示为ω∈［0.2，1.65］区间时系统经历逆倍化分岔过程的相图与Poincaré映射图的叠加，可以清晰地观察到这一系列分岔过程。

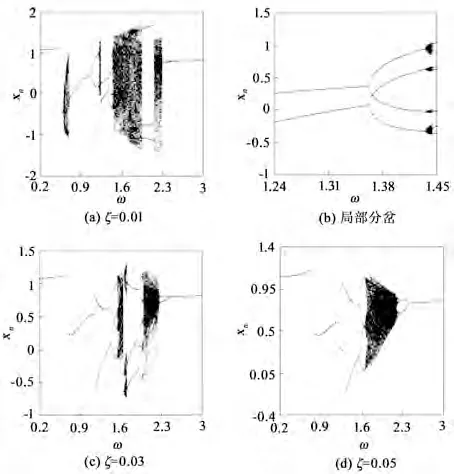
图2 不同啮合阻尼比条件下系统分岔

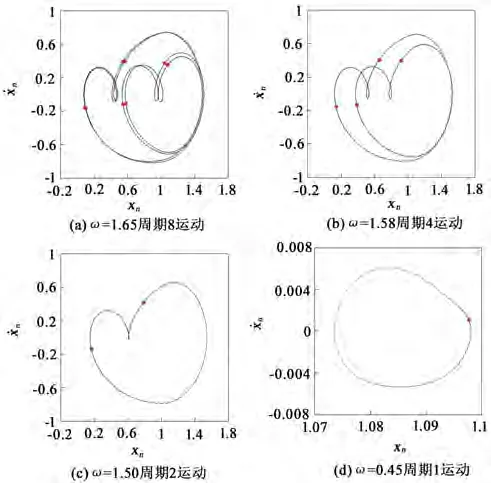
图3 逆倍化分岔过程

图3中，xn为无量纲相对位移；为无量纲相对速度；ω为无量纲啮合频率。

2.2 输入载荷对系统分岔特性的影响

保持系统基准参数不变，综合考虑取系统啮合阻尼比ξ=0.03。通过改变无量纲输入载荷的值，进行数值分析，得到如图4所示的系统分岔图。

通过图4（a）可以观察到，在无量纲输入载荷p1=0.027条件下，系统在啮合频率ω＞2.28时呈现出稳定的周期1运动状态。当啮合频率ω递减穿越2.28时，系统的周期1运动经倍化分岔进入周期2运动状态，随后在啮合频率递减穿越ω=2.145时，系统再次经倍化分岔进入短暂的周期4运动状态。随着ω继续递减，系统的周期运动变得更加多样。在ω∈［1.24，2.125］和ω∈［0.96，1.065］的区域，系统出现了被周期运动间隔开来的大面积混沌运动，其中，ω∈［1.24，2.125］区间内出现了极小范围的周期窗口。从啮合频率ω=1.24开始递减，系统依次呈现的周期运动分别是周期8—周期4—周期2—周期4—周期2—周期1运动。其中周期1运动并不是一直表现出稳定状态，在ω递减穿越ω=0.57后，系统发生跳跃分岔，之后系统才趋于稳定。

另一方面，在无量纲输入载荷p1=0.048的基础上，将p1增大至0.063，其分岔图如图4（b）所示。在啮合频率ω递减至2.3时，系统依次发生周期一—周期二—周期四的倍周期分岔序列。ω继续递减，在ω∈［1.75，2.3］区间，系统呈现出大幅的混沌啮合运动。如ω=2.0时，系统的Poincaré映射图为一系列杂乱的密集点，相轨迹形成不封闭的曲线，如图5所示，证明此时确实是混沌运动。在啮合频率穿越ω=1.75时，系统从混沌运动退化为周期8运动。并且经历一系列逆倍化分岔，即周期8—周期4—周期2—周期1和两次跳跃分岔，分别发生在ω=1.25和ω=0.71之后，系统最终转迁为稳定周期1运动状态。

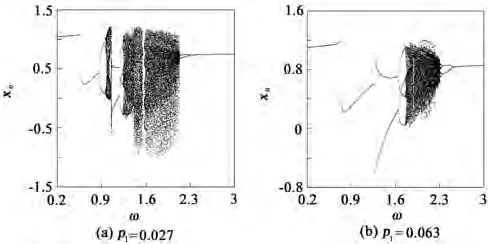
图4 不同输入载荷条件下系统分岔

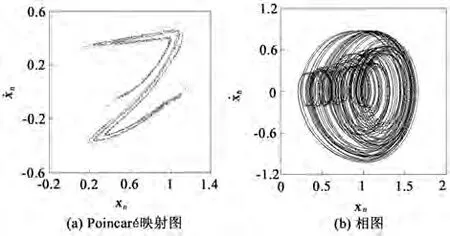
图5 ω=2.0 Poincaré映射图和相图

3 磨损条件下动力学行为研究

斜齿轮相比直齿轮而言，其啮合过程是一个过渡的过程，齿面的力是由小到大，再由大到小逐渐增加的。并且其重合度较大，所以适用于高速重载的场合。正是由于重载的因素，长期运转的斜齿轮系统便会发生磨损。如果忽视磨损等问题，就会造成意想不到的事故，故而对于磨损状态下运转的斜齿轮，有必要研究其动力学行为。

齿轮磨损会直接导致齿轮啮合间隙增大，主要可以分为单齿磨损和多齿磨损（或全齿磨损）两种状态。这里结合实际情况，以全齿均匀磨损来进行研究。

当全齿磨损故障发生时，可以用新的齿侧间隙函数f1（t）来作近似模拟［10］。

f1（t）可表示为：

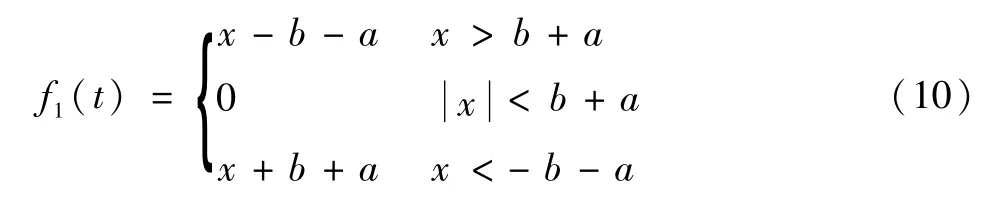
式中：b为原始无量纲齿侧间隙为1.0；a为磨损故障的齿侧间隙，即全齿磨损的剧烈程度。

磨损状态系统分岔图如图6所示。为了方便与正常运转状态作比较，保持系统基准参数不变，取啮合阻尼比ξ=0.03。首先取a=0.1来模拟轻微磨损故障，得到如图6（a）所示的全局分岔图。对比图6（a）与图2（c），斜齿轮系统在轻微磨损状态下的分岔图变化不大。在高频区域，依旧是经过倍化分岔进入混沌运动，但是倍化分岔的区间有所减小。而更加明显的区别在于，两段混沌运动之间嵌入的周期六运动几乎消失不见，周期三窗口也略微有所减小。另一点主要区别在于，当啮合频率ω∈［1.0，1.3］区域时，系统不再是稳定的周期运动，如图6（b）为ω∈［1.0，1.3］的局部分岔图。具体表现为ω＞1.132时为混沌运动，ω＜1.132时为稳定周期运动，可通过图7所示的相图和Poincaré映射图加以验证。

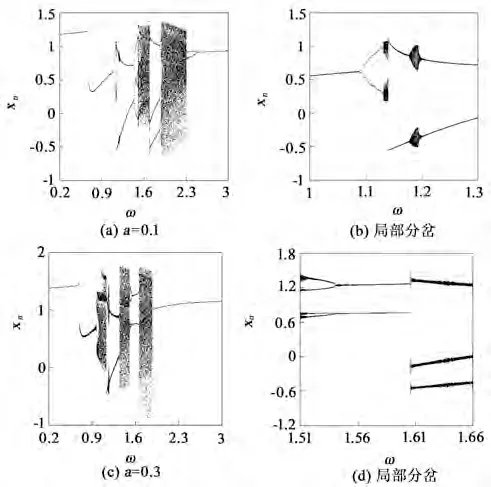
图6 磨损状态系统分岔

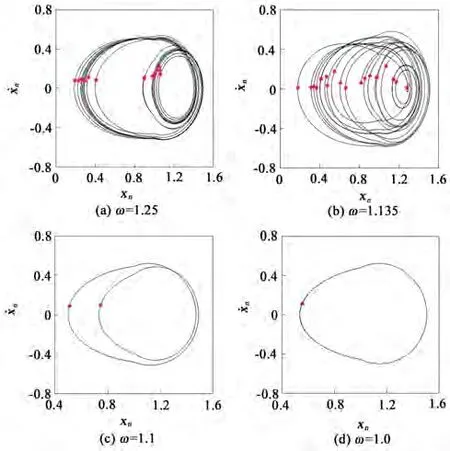
图7 轻微磨损故障相图及Poincaré映射图

取a=0.3来模拟齿轮系统剧烈磨损状态，得到系统分岔图如图6（c）所示。当ω＞1.88时，系统处于稳定周期1运动状态，当ω穿越1.88时，周期1运动经Hopf分岔转迁为概周期或混沌运动，直到ω穿越0.7时，系统经跳跃分岔退化为稳定周期1运动状态，结束一系列混沌运动。图6（d）为ω∈［1.51，1.66］的系统局部分岔图，可以看到，此区间并非周期运动，而是混沌运动区间。

4 结束语

本文针对斜齿轮系统，建立包含齿侧间隙、轴承间隙和啮合阻尼比等在内的齿轮系统非线性动力学模型。通过对斜齿轮系统动力学行为的研究，得出如下结论。

（1）在斜齿轮系统中，啮合阻尼比的改变会使得系统的周期运动形式多样化。当啮合阻尼比较大时，系统的混沌啮合运动区间比较集中，分岔形式比较单一。随着啮合阻尼比的减小，系统会出现阵发性混沌区域，并且混沌区域的无量纲相对位移幅值更大。说明此时系统的冲击猛烈、稳定性弱。

（2）输入载荷的改变也会对系统产生较大的影响。具体表现为输入载荷很小时，系统处于中频运转时基本上全是混沌啮合运动，此时对齿轮系统以及整个机械设备都有极大的负面影响。而伴随着输入载荷的增加，混沌区域会有明显的缩小，并且在中频运转向低频过渡时混沌运动被周期运动取代，稳定周期运动所占比值增加。输入载荷越大，系统的周期运动形式越单调，越趋于稳定。

（3）在轻微磨损状态下，系统的运行状态变化不大，只是对低中频区间有着微小的负面影响。而在剧烈磨损的条件下，整个系统在中频区域皆处于混沌运动状态，说明此时齿轮系统已经出现严重的隐患，有必要考虑对齿轮进行处理，例如更换润滑油或者直接更换齿轮，以免发生事故。