创新环境指数构建及基于自适应ARIMA的动态预警监控研究

谢贤芬,王斌会,古万荣,杨 颖

(1.暨南大学 a.经济学院;b.管理学院,广东 广州 510632;2.华南农业大学 数学与信息学院,广东 广州 510642;3.中南大学 法学院,湖南 长沙 410083)

一、引言及文献述评

创新是推动国家和地区经济增长和发展的驱动力,在经济发展过程中,单纯依赖市场的自由引导或企业的自主创新力量往往不够,需要依靠整个创新系统。创新系统是各级政府部门、高等院校、地区科研机构及企业等实体单位协调运作,形成的有机复杂网络系统,在面对全球经济危机及适应城市经济衰退的冲击下,区域或省域经济区的创新系统表现出了较完备的抗风险能力[1]。为此,学术界对创新系统从各方面进行了深入研究,创新理论得到了迅速发展。从地区跨度来看,创新系统分为国家级创新系统、区域级创新系统和城市级创新系统。典型的国家级创新系统包括全球创新指数GII及欧洲创新记分牌EIS,以及中国两个国家创新能力评价系统:中国创新指数和国家创新指数,这些均用来反映国家的创新能力及发展趋势[2]。国内外学者对区域级创新系统及城市级创新系统做了广泛的研究,美国用来评价城市创新程度的指标体系是“创新力指数”,澳大利亚和英国也使用该指数来衡量城市创新程度[3]。中国区域级或省级创新系统中,较为认可的有《中国区域创新能力报告》、中国城市创新力指数和中国创新能力评价。纵观国内外学者的研究,衡量创新系统的各类研究也日益增多,主要有:创新能力研究、创新环境研究、创新发展研究、创新绩效研究、创新空间关联研究等[4-6]。

本文主要研究创新系统中的创新环境。20世纪80年代GREMI提出创新环境的概念,最初的涵义主要包括创新环境的定义及构建、创新环境与经济发展的关系、创新环境对创新绩效的影响研究三个方面。创新环境是指某一特定区域内聚集资源的再分配,包含两个层面的涵义:第一个层面是指单个或少数几个关联企业内部的创新环境,如企业管理者的冒险、企业应对市场机会的能力、企业自身资源的合理配置等,这是微观层面的创新环境状态;第二个层面是指企业所处的外部环境创新,包括经济环境、劳动力市场、技术水平、区域文化等因素,这是宏观层面的创新环境状态。

创新环境状态及指数研究最近受到国内外学者的重视,由于不同文献研究的数据、时间范畴、模型、国情等因素的不同,分析过程和得出的结论也不尽相同。国内外相关研究多见于创新环境指标体系研究与构建、创新环境的测度方法、创新环境发展的对策研究等方向。在创新环境指标体系构建的研究工作中,国外学者Michael E.Porter等基于17个区域20多年的数据进行研究,发现硬件条件完善有利于提升区域的创新环境[7];Porter认为产业聚集有利于良好创新环境的创造,产业集群内的企业往往能够更快发展,以更低的成本快速实现企业的创新,同时,相关政策制度及市场也是影响创新环境的重要因素[8];学者Martina Fromhold-Eisebith从社会资本对创新环境的影响因素分析出发,结合德国Aachen地区的真实情况,分析两者之间的相关性及差异性,发现相关性及差异性是相互作用的,这种协同作用有利于提升创新环境[9]。Collins等研究了欧洲企业创新的政策环境,发现地区的政策环境能够极大地鼓励并引导企业进行技术创新,对创新活动推进具有显著的意义[10];杨毅同样认可政策环境的重要性,认为应加大政策层面对创新环境的引导和扶持力度,从而提升技术创新活动的活跃程度[11];施蕾等从基础条件、人力资源、孵化能力和研发转移4个层次构建了包括20个基础指标的创新环境评价指标体系,从省域的角度进行比较研究,结合陕西省实际情况,深入探究其不足之处,并给出相应的对策建议[12]。李玲等首次构建了区域包容性创新环境指标体系,该指标体系既涵盖了创新环境的基础设施、支撑条件、市场及金融环境方面,也涉及创新主体、创新投资、企业的创新能力和制度环境等四个方面[13]。

在创新环境测度分析方面,大部分研究主要是建立各种模型评价各省份在一个时间点的创新环境,分析区域的创新能力差距并尝试解释产生差距的原因,它们并不能对各区域的创新环境状态进行纵向的动态分析。崔航采用层次分析法对中国典型的六大城市群(长三角、珠三角、京津翼、成渝、武汉、哈长)进行实证分析,基于收集的创新环境指标数据进行评价,对各个城市群的不同维度进行了详细分析,同样采用层次分析法的有党晶晶等人[14-15]。黄玲雁构建涵盖经济环境、金融环境、基础设施环境因素的创新环境指标体系,利用因子分析法对湖南省14个地级市的创新环境进行评价与分析,揭示了省域间的差异性[16]。陈红川采用CURE聚类分析算法对高新技术企业的创新环境进行了综合分析,从政策环境、市场环境、人才环境等多个角度进行了细化及分析[17]。鉴于多数文献常采用单一的评价方法进行测度,李沃源等将层次分析法、集对分析法、灰色关联法和TOPSIS结合起来,建立了基于离差最大化的组合评价模型,该模型解决了应用单一方法的不足,并对西部地区科技创新环境的区域差异性进行分析[18]。另外还有一些文献是以创新环境来解释区域创新能力或区域创新效率,结合各种模型研究创新环境对它们的影响[19]。

创新环境发展的对策研究方面,苏炜从基础设施环境、经济环境及创新的产出等多个方面综合评价了珠三角九大国家级自主创新示范区的创新环境,结合各地的实际情况,提出了持续高创新投入、加强基础设施建设工作、建立多元化的创新投入新机制、完善创新体制等多项政策措施[20]。林媛媛等通过分析福建省的环境规划、企业技术创新现状和环境规制低效率原因三方面因素,对福建省企业的发展提供了研究对策[21]。

纵观学者们的研究,他们大多采用的是事件分析法,即在构建创新环境指标体系的基础上,分析过去确定时间段的创新环境状态,但是缺乏对未来创新环境发展状态走向的预测及监控。如何衡量一个国家或地区的创新环境状态并进行预测呢?笔者认为应构建一个综合性指标(指数)来进行测度,目前暂未发现有其他文献构建创新环境指数,对创新环境指数进行预警监测的相关文献也未见报道。

本文从宏观角度去研究创新环境状态的相关因素,构建指标体系,进而建立预警机制,而不是纯粹作为区域创新能力或区域创新效率的解释变量。另外,创新环境发展过程涉及的经济运行指标之间往往存在着相关关系,传统的主成分合成指数法通常要求数据相互独立,直接采用传统主成分合成指数法可能得到不合理的结论。因此,这里利用稳健主成分合成指数法构建宏观创新环境指数MacroIEI(Macro Innovation Environment Indicator),基于自适应ARIMA方法及改进型EWMA控制图建立创新环境指数的动态预警模型,研究指标的动态规律并给出相应的政策建议,以供决策部门或相关企业参考,这为中国区域创新环境的测度提供了新的研究思路,对创新环境预警系统的建立也有一定的意义[22]。

二、动态预警模型与方法

(一)创新环境状态指标体系

本文在宏观层次下构建创新环境状态指标体系,指标选取应能覆盖影响创新环境的经济与社会因素、硬件投入、市场机会等方面。这里参考了国家统计局社科文司“中国创新指数(CII)研究”课题组(2014)提出的指标体系框架,该文提出创新环境领域应能反映驱动创新能力发展必备的人力、财力等基础条件的支撑情况,以及政策环境对创新的引导和扶持力度,共包括经济活动人口中大专及以上学历人数、人均GDP、信息化、科技拨款占财政拨款的比重、享受加计扣除减免税企业所占比重五个指标[23]。然而在实际应用中,有些参数可能会缺失,可以用相关或相近指标来代替。比如,这里的信息化及享受加计扣除减免税企业所占比重两个指标数据缺失,同时使用本科以上学历人数指标替代大专及以上学历人数指标、产值超亿元企业数量替代享受加计扣除减免税企业等。

鉴于上述的数据可获取性以及统计口径的差异性,从经济因素、制度因素、人才因素、硬件能力及产业聚集五个层次出发,选取的创新环境状态指标主要包括专业机构服务数、入园企业数量、企业固定资产投资、财政科技支出、高新区鼓励创新的政策及措施数量、本科以上学历人数、R&D人员数、高新区从业人员数、R&D经费支出、高新区高新技术产品出口总额、高新区GDP、高新技术产品产值、产值超亿元企业数量等13个相关指标。有些原始数据不能很好地反映创新环境状态,本文提出构建比率指标,即用增长率=(当期指标值-上一期指标值)/上一期指标值来表示,总体创新环境指标体系见表1。

表1 创新环境状态指标体系

专业机构服务数增长率及入园企业数增长率用来反映地区经济的发展能力;财政科技支出增长率及企业固定资产投资增长率用来反映地区的创新投入及市场经济水平;高新区相关政策措施增长率指标表明国家/地区对创新园区从宏观角度进行引导及支持的程度,是政府政策调控的有力支撑;本科以上学历占高新区从业人员比重及R&D人员占高新区从业人员比重,能反映地区的劳动者结构及整体素质,是创新发展必备的人力条件;R&D经费支出增长率和高新技术产品出口总额增长率,反映一个地区创新环境的研发投入及硬件水平;高新区GDP增长率、高新技术产品产值增长率和产值超亿元企业数量增长率三大指标,是地区产业聚集效应的最直接表现,而产业聚集跟产出规模又是相互影响的,较大的产出规模将吸引更多优势企业聚集,产业的聚集又提高了资源共享,提高地区竞争力,从而实现更大的产出规模。

(二)创新环境指数计算方法

主成分分析方法的全称为Principal Component Analysis,通常简记为PCA,该方法最早是由Pearson在1901年提出来的,现在使用的PCA技术是经过Hotelling改进的,其基本思想便是数据降维,通过对数据压缩把原来若干个映射同一个问题的研究数据xi解释成一个新的相互无关的综合指标yi,这个指标被称为主成分,它们之间有如下的公式:

(1)

记标准化数据矩阵为Zn×p,建立变量的相关系数矩阵:R=(rij)p×p=Z′Z,然后求出相关矩阵R的特征值λ1≥λ2≥…≥λp>0及相应的单位特征向量u1,u2,…,up,写出主成分:yi=ui1z1+ui2z2+…uipzp,这里i=1,2,…,p。

根据累积方差贡献率高于80%的基本原则,选定前m个主成分反映原评价对象。设前m个主成分为:C1,C2,C3,…,Cm,以方差贡献率为权重,可以得到综合评价函数:

(2)

将主成分综合得分值作为主成分合成指数值(PCSI),PCSI=C。通过该指数可以很好地反映宏观经济运行指数的动态变化过程。

然而,从上面的传统主成分构建过程可以看到,主成分的计算基于协方差矩阵(或标准化矩阵),并在此基础上计算其他统计量。由于协方差矩阵是不稳健的,因此样本中出现离群值时,相关系数矩阵、特征值和特征向量会受到较大影响,进而得到不准确的计算结果。2007年王斌会提出了基于FAST-MCD算法构建稳健的均值向量和协方差矩阵,并应用到主成分分析中,通过模拟和实证研究发现,改进后的主成分分析方法确实能够对离群值起到很好的抵抗作用[22]。稳健主成分合成指数构建的具体算法如下:

(1)获取经济运行样本数据,并进行标准化,记为Z;

(2)基于Fast-MCD算法得到协方差矩阵S和稳健均值向量T;

(3)通过协方差矩阵S得到稳健相关矩阵R;

(4)求解矩阵的特征方程,可得稳健相关矩阵R的特征值λp和特征向量up;

(5)写出主成分yi(i=1,2,…,p),按累积方差贡献率大于80%的原则,取前m个主成分计算综合得分。

按上述方法得到的综合得分值即为稳健主成分合成指数值,记为:PCSIm。本文将以此构建宏观创新环境指数MacroIEI,即:MacroIEI=PCSIm。

(三)基于自适应ARIMA方法的创新环境指数预警模型

1.基于自适应ARIMA的预测方法

ARIMA模型(自回归求积移动平均模型)是一个经典的时间序列预测方法,其基本原理是:先利用d阶差分将非平稳时间序列平稳化,然后对平稳化后的时间序列,利用自回归过程AR(p)、移动平均过程MA(q)以及样本自相关系数(ACF)和偏自相关系数(PCF)等对模型进行辨识,该模型常用于时间序列分析。

如果某个时间序列{Xt}的d次差分Wt=(1-B)dXt是一个平稳的ARMA过程,则称{Xt}为自回归移动平均求和模型。如果Wt服从ARMA(p,q)模型,则称{Xt}是ARIMA(p,d,q)过程。ARIMA包含了自回归、差分以及移动平均三个组成部分,p、d、q分别表示自回归阶数、差分次数和移动平均的阶数。在实际应用中,通常取d=1或2。这时可用平稳过程Wt来代替不平稳的Xt在ARMA模型中的位置,即:

Wt=c+φ1Wt-1+…+φpWt-p+εt+θtεt-1+…+θqεt-q

(3)

用滞后算子表示,则有:

Φ(B)Wt=c+Θ(B)εt

(4)

其中,Φ(B)=1-φ1B-φ2B2-…-φpBp,Θ(B)=1+θ1B+θ2B2+…+θqBq。经过d阶差分变换后的ARMA(p,q)模型称为ARIMA(p,d,q)模型,式(3)等价于下式:

Φ(B)(1-B)dXt=c+Θ(B)εt

(5)

其中{εt}是白噪声过程。模型ARIMA(p,d,q)的识别和参数估计步骤与ARMA(p,q)模型的参数估计基本类似。对于ARIMA(p,d,q)模型,参数d的确定由差分次数来决定。ARMA(p,q)模型的识别方法较多,一般会利用ACF函数和PACF函数来判断类型。初始值的选择往往是不准确的,需要根据模型的检验结果对参数不断进行调整,最终得到最优模型。估计模型的参数有两种常见的方法:最小二乘法和极大似然法,这两种方法都是“精估计”。本文提出一种自适应方法,利用R统计软件自编了adaptive.Arima()函数,对R自带的auto.arima()函数进行了改进。该函数能够绘制模型的识别过程图,并给出最优模型的参数估计值及序列的预测值。另外,由于经济运行数据可能具有季节因素,如CPI指数的周期长度为12,这里在实现adaptive.Arima()时考虑了对数据进行季节ARIMA模型的估计。adaptive.Arima()的基本模型如下:

adaptive.Arima(y,d=NA,D=NA,max.p=5,max.q=5,max.P=2,max.Q=2,max.order=5,max.d=2,max.D=1,…)

adaptive.Arima()的基本思想是对ARIMA建模的系数进行逐步向后选择的过程,其原理类似于线性回归模型的逐步回归过程,基于极大似然估计和AIC/BIC/AICC进行模型的选择,这里主要采用AIC最小准则选择最优模型。

图1是以高新区GDP指数为例说明adaptive.Arima()的模型识别过程,每一行对应于每一步的后向选择。每个小方格中的数字是对应的系数,系数值越大其对应的小方格颜色就越深。每个小方格右下角的小三角形代表该系数的p值,p值介于0～0.1之间,p值越大,对应的灰色就越深,p为0.1时为黑色。图形的左边是在每一步骤中建立的模型的AIC值,右侧的sar是对应的AR模型的残差项系数值,sma是对应的MA模型的残差项系数值。根据AIC最小准则,这里选择迭代4次之后建立的ARIMA模型。从图1及adaptive.Arima()函数的运行结果得到的最优模型为:

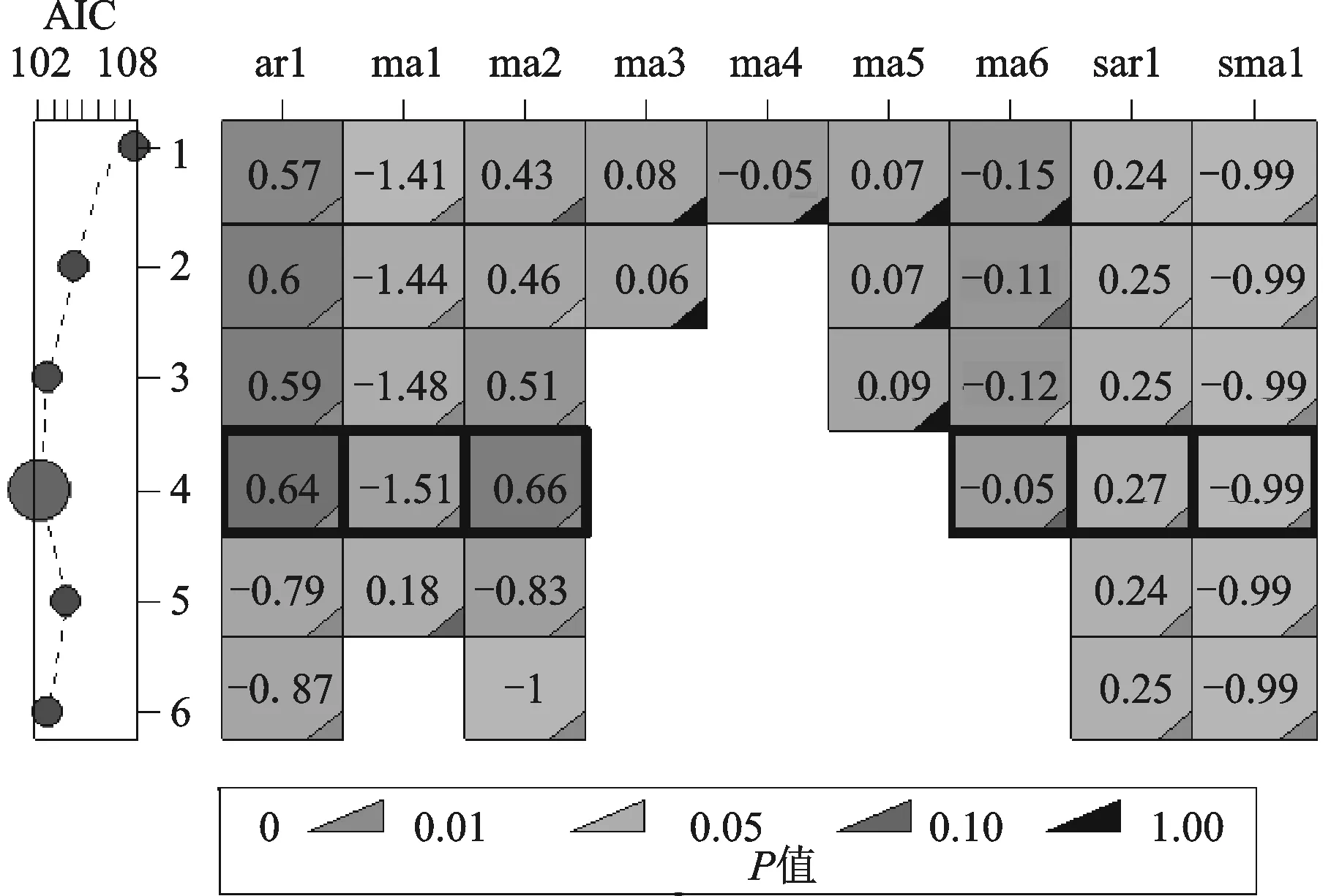
图1 1997—2019年高新区GDP的ARIMA模型识别过程图

ARIMA(p=1,d=1,q=c(1,2,6))×(P=1,D=1,Q=1)7

2.构建基于改进型EWMA的动态预警模型

1959年Roberts提出了指数加权移动平均(EWMA)控制图,它与累积和控制图(CUSUM)一样,要求观测序列值相互独立。然而,经济运行时间序列数据往往存在着自相关现象,若直接采用传统的EWMA控制图进行过程控制,估计出的过程方差是有偏的。这里,将采用考虑了自相关关系的改进型EWMA控制图,并把上节中基于自适应ARIMA方法得到的预测结果加入到该控制图中,从而实现对创新环境指数进行动态过程控制。改进型EWMA控制图的原理如下:

设{Xt}是离散平稳过程,EWMA统计量Zt、自协方差函数R(τ)=cov(Xt,Xt+τ)=E[(Xt-μ)(Xt+τ-μ)]仅与滞后期有关。统计量Zt及序列{Zt}的自协方差函数如下:

(6)

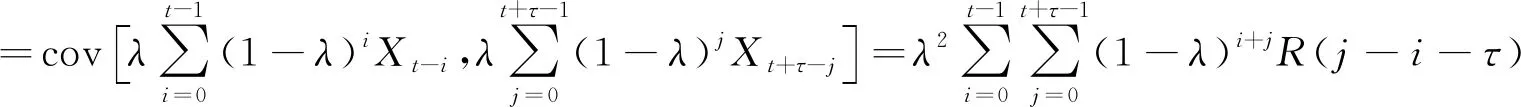
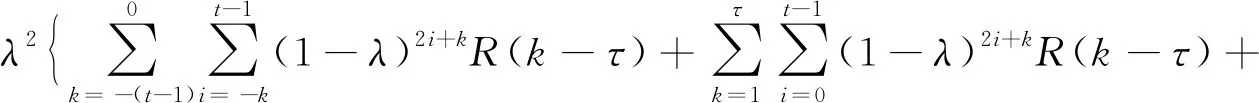
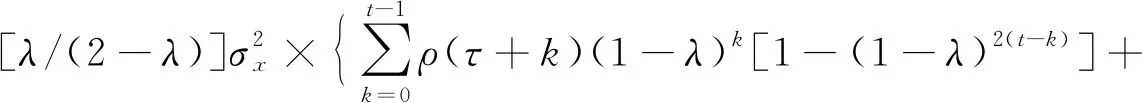
(7)

在式(6)中,λ是一个常数,取值范围为:0<λ≤1,EWMA统计量的初值Z0一般取E(X)=μ。在式(7)中,ρ(k)=R(k)/R(0)表示{Xt}后面k期的自相关系数。当τ=0时,式(7)即为Zt的方差:

(8)

当t→∞时,cov(Zt,Zt+τ)收敛且收敛值不依赖于t。由于cov(Zt,Zt+τ)收敛,则当t很大时,由式(7)可知存在常数M,使得:

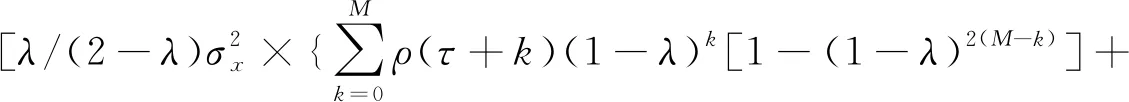
(9)

那么,Zt的近似方差为:

(10)

而Hunter及Zhang等人已经证明了Z在自相关条件下的数学期望为[24-25]:

E(Z)=E(X)=μ

(11)

(12)

本文将利用上述方法对创新环境指数MacroIEI进行过程控制,若计算得到的统计量观测值全部落在式(12)对应的控制线内,表明不存在离群值;否则,则存在离群值,需对离群值作进一步分析。由于在对创新环境指数进行实际的过程控制时,控制统计量Zt的均值及方差会受到样本均值、样本自协方差及相关系数的影响,为了减少相关因素对控制参数估计准确度的影响,样本数量不宜太少。

三、分析过程和结果

(一)样本数据及描述性统计分析

我们使用创新环境状态指标体系(见表1)中的广东省高新技术企业年度数据,样本期为1997—2019年,指标数据来自《广东统计年鉴》及《广东科技年鉴》,表2罗列了各指标变量的定义及基本描述性统计结果。

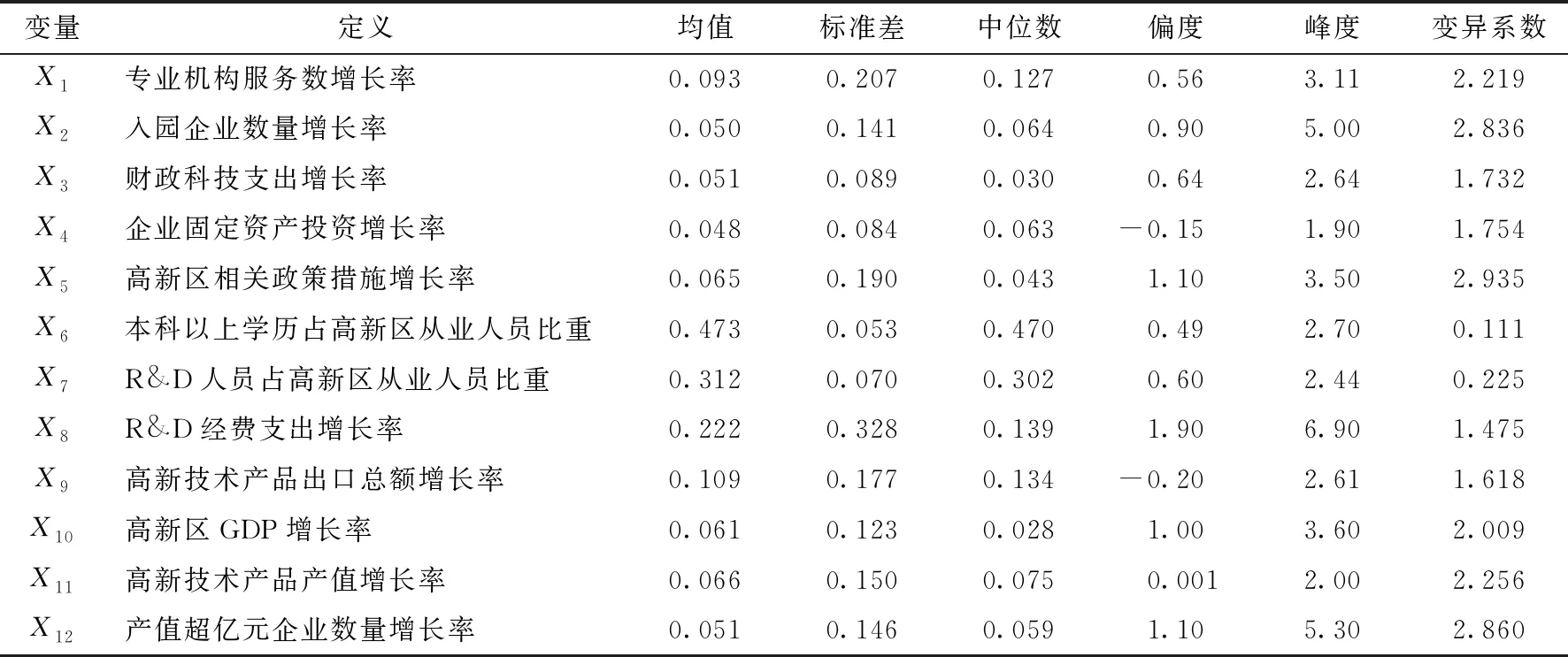
表2 描述性统计分析

从表2可以看出,只有X6(本科以上学历占高新区从业人员比重)及X7(R&D人员占高新区从业人员比重)指标的均值大于标准差,其他变量的标准差均很大,偏离均值较多,说明这些变量是非正态的。比如入园企业数量增长率X2,其均值为0.050,标准差为0.141,约为均值的3倍,产值超亿元企业数量增长率X12的均值为0.051,标准差为0.146,也约为均值的3倍,这两者都不符合非正态分布。此外,从Skewness和Kurtosis两个统计量值也可以分析出这些数据不服从正态分布。

这里还引入了变异系数对各指标进行测度,变异系数值越小,说明数据的波动程度越小,变异系数值越大说明数据的波动程度越大,更可能存在离群值,从而影响创新环境的状态。如X2的变异系数为2.836,X6的变异系数为0.111,说明X2的变动要比X6的大,表示在样本期内入园企业数量增长率变量的波动较大,这与广东省对高新区的投入息息相关,包括财政科技投入、政策环境对企业创新的扶持力度(如企业享受减免税收优惠政策)、产业聚集等因素。另外,衡量地区产业聚集效应的三大指标为:高新区GDP增长率(X10)、高新技术产品产值增长率(X11)和产值超亿元企业数量增长率(X12),它们的变异系数值也较大,均大于2.0,进一步验证了产业聚集和产出规模的正向反馈作用,产出规模提升有利于促进产业聚集,而产业聚集反过来又能实现更大规模产出。

(二)广东省创新环境状态综合评价

基于表1的创新环境状态各项指标,运用稳健主成分合成指数法计算得到相关数据见表3。从表3可知,前5个特征值的累积方差贡献率超过了80%,说明这5个主成分包含了大部分状态指标的信息,这些主成分对应的载荷矩阵如表4所示。

表3 特征值、方差贡献率及累积贡献率

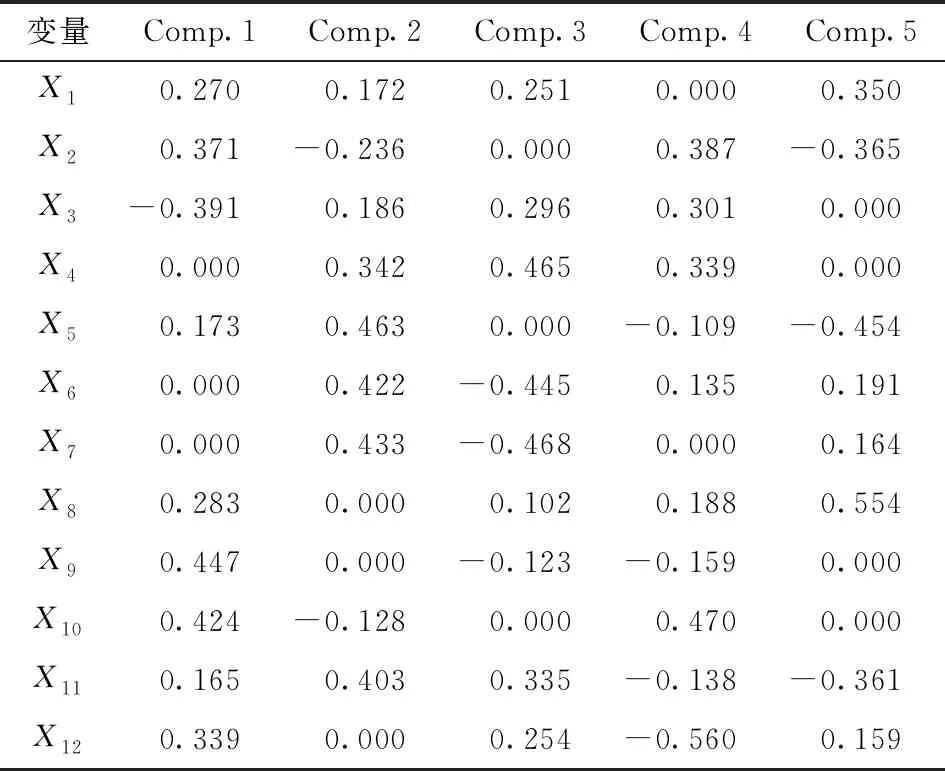
表4 主成分载荷

对前5个主成分按方差贡献率进行加权计算,利用创新环境指数计算方法获得各年份的稳健主成分合成指数值,即创新环境指数MacroIEI,绘制其走势图如图2所示。

图2 1997—2019年广东省创新环境指数走势图

从图2可以看出,在整个研究期内,广东省创新环境指数处于一个波动的状态。其中,有3个时间段的波动幅度较大,分别为:2001—2002年、2003—2005年和2007—2011年。以2008年至2009年为例,2008年的指数值为1.219 2,2009年的指数值为-0.589 1,波动差为1.808 3,是整个研究期内波动幅度最大的。总体而言,创新环境指数的变动受到宏观政策、外部环境、地区政府投入、经济因素等方面的影响,后续的预警监控分析中将作更详细的分析。

(三)估计方法和结果

1.平稳性检验

平稳是建立时间序列模型的前提,为了确定创新环境指数不存在随机趋势或确定趋势,应对该变量进行平稳性检验。本文采用ADF(Augmented Dickey-Fuller Test)方法来检验该变量序列的平稳性情况。对广东省高新技术产业创新环境指数MacroIEI进行平稳性检验,结果显示其不平稳。从图2的MacroIEI走势图可以看出,该时间序列不呈现指数增长趋势,因此采用差分法进行平稳化。经一阶差分后,序列d.MacroIEI的ADF检验结果为平稳,见表5。

表5 平稳性检验结果

2.初步相关性分析及模型确定

对一阶差分d.MacroIEI序列进行数据的相关性及正态性检验,从序列数据的ACF图和偏PACF图(图3)可以看出,ACF很明显是“2后截尾”,而PACF图中有若干项非0而呈现出振荡拖尾的现象,可初步判断序列d.MacroIEI序列应为ARIMA(p,0,q)模型(p不为0)。

图3 d.MacroIEI的自相关图和偏自相关图

另外,对序列数据d.MacroIEI进行正态性检验,从其直方图及QQ图(见图4)可以看出,基本符合正态分布。由于数据序列样本量为20多个,这里采用小样本的正态性检验方法Shapiro-Wilk进行检验,得到的W=0.934 8,p值为0.170 8>0.05,结果认为该样本数据符合正态分布。

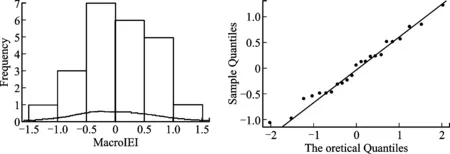
图4 d.MacroIEI的直方图和QQ图

我们利用提出的自适应ARIMA方法,即利用adaptive.Arima()函数对模型进行识别,并对模型的最佳参数进行估计,以AIC(Akaike information criterion)最小准则AIC=-2ln(L)+2k和BIC(Bayesian Information Criterion)最小准则BIC=-2ln(L)+kln(n)来选择最佳模型,其中L为最大似然函数,n为样本数量,k为模型的参数个数。这里基于实际数据,设置初始值为p=6、d=1、q=1,初始的完全模型为ARIMA(p=6,d=1,q=1),即有:

Yt=-1.675Yt-1-1.580Yt-2-1.183Yt-3-0.603Yt-4+0.003Yt-5+0.201Yt-6+0.519εt-1

该初始模型对应的AIC值为53.93,BIC值为55.72,极大似然估计值为-18.96。基于该初始模型调用adaptive.Arima()方法进行逐步向后选择,最终得到的最佳模型是:ARIMA(p=4,d=1,q=0),对应的AIC值为48.58,BIC值为54.04,极大似然估计值为-19.92,该模型的系数估计值见表6。

表6 创新环境指数差分序列d.MacroIEI拟合结果

ARIMA(4,1,0)模型为:

Yt=-1.182Yt-1-1.017Yt-2-0.73Yt-3-0.348Yt-4

这里,Yt为原始序列作d=1阶差分后得到的序列,即:d.MacroIEI。此时,基于拟合的ARIMA模型,向前预测两期,得到序列d.MacroIEI的预测值为0.697 3及0.337 1,将它们代入到一阶差分计算公式,即可得到广东省创新环境指数MacroIEI在2020年和2021年的预测值,分别为-0.184 9和0.152 2,其预测走势图见图5。

图5 创新环境指数MacroIEI的预测走势图

从图5可以看出,2018年的创新环境指数值比2017年的指数值有较大幅度增长,2019年的指数值开始下降,比2018年下降了0.292 3,下降的幅度较小。预测的2020年指数值接着下降,比2019年下降了0.697 3,而2021年相比2020年又是增加的,从-0.184 9增加到0.152 2,增幅为0.337 1。从整体上看,创新环境指数呈现出缓慢增长的趋势。

3.建立动态EWMA预警监测模型

对加入了预测值的创新环境指数MacroIEI数据进行动态过程监控,而使用常规控制图的基本假设前提是:一是质量特征值相互独立;二是质量特征值服从正态分布。实际的经济运行过程中,直接获得的经济运行时间序列数据往往并不满足“服从正态分布”和“数据间互不相关”这两个基本条件。因此,需要对指数MacroIEI进行平稳性、正态性及相关性检验。

检验过程类似于上一节,对加入了两期预测数据的MacroIEI进行一阶差分,得到序列d.MacroIEI_p,对该序列进行ADF检验,检验结果为Dickey-Fuller=-3.92,p值为0.00,结果平稳,表明一阶差分后的序列基本消除了趋势。对该序列进行Shapiro-Wilk正态性检验,W=0.978 2,p值为0.270 3>0.05,该结果认为样本数据是来自正态分布的总体。这里省略对序列数据作ACF图和偏PACF图,因为结果跟上文的d.MacroICI类似。

由于创新环境指数的一阶差分序列d.MacroIEI_p存在自相关现象,这里采用改进型EWMA控制图进行预警监测,同时也应用常规EWMA控制图进行过程监控,结果分别见图6、图7。

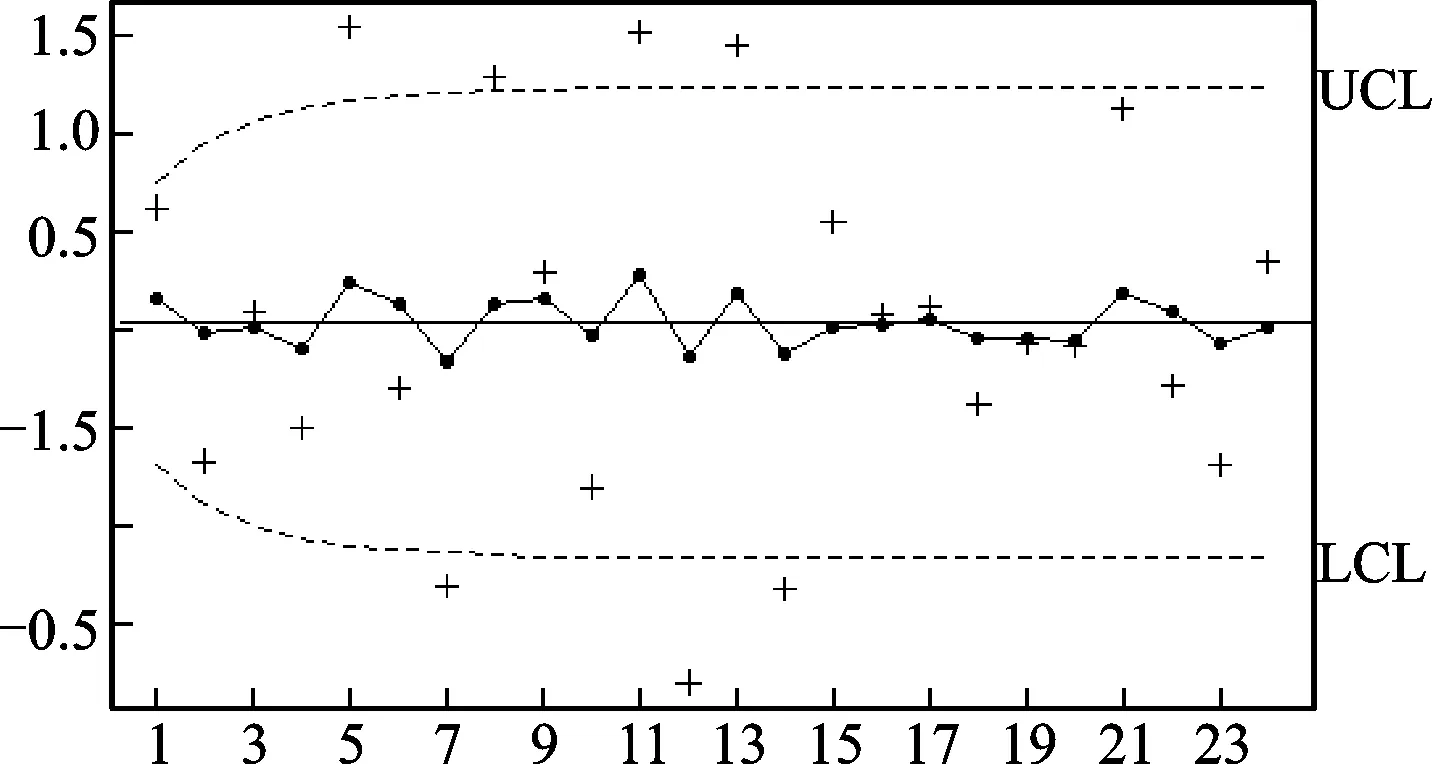
图6 基于常规EWMA控制图的过程控制图

图7 基于改进型EWMA控制图过程控制图

在过程控制图中有三条特殊的水平直线,如图6,UCL为上控制线,LCL为下控制线,中间水平直线为中心线CL。当检测统计量的观测值落在上下控制线外的区域时,认为过程不处于受控状态,控制图将给出过程失控的警报,即该观测值为可能“离群值”。

从常规EWMA控制图可以看到,所有样本数据点及预测数据均落在控制限区域内,均不存在异常情况。对于改进型EWMA控制图,我们可以看到,一共有四个点是落在控制线外的,分别是2002年、2008年、2009年、2010年,而其他年份的真实值及两个预测数据值都落在控制线内。

结合广东省实际的创新环境情况,改进型EWMA控制图判断出的四个离群值是更符合实际的。(1)2008年底,中国受到美国严重的次贷危机影响,整个大环境的社会经济状态是属于一个下降(安全状况降低)的情况,受其影响的创新创业环境状态落在了控制线之外,这种情况更符合当时的实际情况。而且这种状态连续持续了三期,多了两个邻近的离群值,包括2009年及2010年,这几个离群值的存在都具有一定的合理性,无论是受到宏观政策、外部环境还是其他一系列经济因素的影响,宏观上创新环境状态的情况在一段时间内应具有一定的持续性,至少是短期的持续性。(2)2002年,虽然广东省创新能力稳居全国第三位,总体水平较高,但是影响创新能力各要素的方法是不平衡的,其中包括整个创新环境状态。首先,2002年广东省研发经费支出中,政府投入部分约占10%,该数据为全国最低,投入明显不足,政府对科技创新的重视程度远远不够。同时,广东省产学研合作还处于一个发展的态势,企业与研究机构、高等院校合作仍不太紧密,特别在某些领域的合作发展方面,学科分布与企业需求不太相符,这也造成了创新环境状态的变动。需要说明的是,落在控制线外的样本数据为离群值,这里的离群值并不一定是指创新环境状况不好的情形,也可能是创新环境状态极好,却远远偏离其他数据的情形,此时应根据实际情况进行分析。

四、研究结论及启示

基于广东省高新技术企业1997—2019年的数据,本文从宏观角度研究创新环境状态的相关因素及指标体系、构建创新环境指数及进行预测预警分析,主要研究结论为:

第一,创新环境状态指标体系涵盖了经济环境及硬件能力、制度及创新人才因素、产业聚集等几个方面,构建出的创新环境指数综合反映出地区在这几个方面的创新环境状态。在对广东省创新环境各指标的实际数据进行变异系数测度时,发现波动程度较大(变异系数值>2.0)的指标包括:两个经济因素指标(专业机构服务数增长率和入园企业数量增长率)、一个制度因素指标(高新区相关政策措施增长率)和三个产业聚集指标(高新区GDP增长率、高新技术产品产值增长率和产值超亿元企业数量增长率)。这几个指标的波动程度类似,也与它们之间的正向相互作用有关。随着高新区科技企业的投入及政策扶持力度加强,会吸引更多优势企业入园,相应带动专业机构服务数量增长;同时,优势企业入园又会提高资源共享及高新区的竞争力,从而带动整个高新区的GDP及技术产品产值增加。因此,为了提升整个高新技术企业的创新环境,政府可持续加大对高新区在各方面的支持力度,加大财政科技投入,继续实施相关税收优惠政策。同时,也应重视变异系数较小的指标,如本科以上学历占高新区从业人员比重,政府可通过制定人才奖励政策等,为高新区引进更多博士和硕士学历人员,加强创新人才队伍建设,这也有利于改善创新环境。

第二,构建了创新环境指数MacroIEI,由于创新环境发展过程涉及的经济运行指标之间往往存在着相关关系,这里采用的是稳健主成分合成指数法。从图2的广东省创新环境指数走势图可以看出,MacroIEI是波动的,且较大的波动后面往往跟着另一个较大的波动,较小的波动后面往往跟着另一个较小的波动,即:波动具有一定的持续性。从整体上看,样本考察期内的创新环境指数呈现出平缓上涨的趋势。

第三,利用自适应ARIMA方法对MacroIEI进行预测,并首次将预警监控技术引入到创新环境状态的研究分析中,利用改进型EWMA控制图对创新环境指数MacroIEI进行预警监控,与并未考虑样本数据相关性的常规EWMA控制图进行比较,发现常规控制图未识别出来的可能离群值,改进型EWMA控制图都识别出来了,且这几个离群值与实际情况较为相符。因此,相比常规控制图EWMA而言,改进型EWMA控制图具有更好的检测效果。

本研究得到的指数趋势及预警监控结论基本符合广东省实际的创新环境状态,在一定程度上验证了构建的创新环境指数的适用性,提出的动态预警监控方法也是合理的,可以依据这些来评价广东省的创新环境状态,进一步构建区域创新环境预警系统,本文采用的模型方法对中国其他地区的创新环境状态研究具有一定的借鉴意义。