一种基于分区段模式土工加筋拉伸应变分析方法
2021-06-24吕伟华刘维正孙信张继周
吕伟华 ,刘维正 ,孙信,张继周
(1.南京林业大学 土木工程学院,江苏 南京 210037;2.中南大学 土木工程学院,湖南 长沙 410075;3.江苏交通控股有限公司,江苏 南京 210016;4.公路地质灾害防治工程技术研究中心,宁夏 银川 750004)
桩承式加筋路堤因具有施工速度快、加固效果优和经济效益好等优点,在公路路堤和铁路路堤等工程中被广泛应用。而在进行桩承式加筋路堤设计时,必须要对这种双向复合增强体的荷载效应进行正确的评估。目前,工程设计人员可参考相关的桩承式路堤理论并考虑土工加筋作用机制评判方法[1−4],也能参考国外相关的手册指南[5−9]。然而,在评价水平加筋影响桩土荷载调配作用时,基于JONES 等[10]理论的英国手册BS8006 将部分路堤荷载完全归由加筋层承担,却把该荷载作了过度计算;德国指南EBGEO[11]在分析加筋薄膜效应时,仅考虑少部分地基反力作用在加筋层上;ABUSHARAR 等[12]直接用圆形挠曲形态构建土工加筋提拉作用与上覆荷载竖向力的平衡;而EEKELEN 等[13]采用一种倒三角形的荷载形式进行加筋层薄膜效应的分析并据此展开竖向应力的平衡计算。综观这些方法,在进行土工加筋的薄膜效应评价时要么仅采用均值应变假设,要么未对筋材的工作模式进行明确判定区分,而且对筋层与填料接触特性的宏观力学表征亦较模糊。虽然部分学者[14−17]将不同荷载形式下土工加筋拉应变分别进行了讨论,也引入了局部筋土界面作用因子,但水平加筋通长范围内的作用机制及定量评价仍需进一步探讨。参考已有的研究文献资料[18−19],本文开展通过橡胶水袋泄水实现基底局部差异沉降的加筋路堤模型试验,分析不同沉降差条件下加筋层挠曲后的拉伸应变分布形式与大小变化规律,基于通长范围内划分为锚固段、过渡段与挠曲段的分区工作模式及拉应变非均匀分布特性,引入筋层与填料接触界面摩擦作用强度指标,推求一种水平向加筋体拉应变分析计算方法,且应用试验实测数据对其合理性进行初步验证。
1 模型试验及结果分析
1.1 试验模型介绍
试验模型所用的路堤填料取自某高速公路拓宽工程现场,模型路堤高度为0.6 m,分6 层填筑,路堤边坡度为1:1.5;所用填土塑限为20.3%,液限为40.8%,塑性指数为20.5,填土黏聚力为8 kPa,内摩擦角为24°;橡胶水袋的长×宽×高=1.6 m×1.0 m×0.3 m,模型填筑过程及控制条件参数见表1 所示。试验模型的具体构造与监测传感器的布置如图1所示。

表1 模型填筑参数与控制条件Table 1 Model filling parameters and control conditions

图1 模型试验设计构造Fig.1 Schematic diagram of model test
试验模型所用土工格栅为TGDG40kN 型单向塑料土工格栅(部分弱化处理),测得其抗拉应变为10.9%时的拉应力为42.3 kN/m。考虑路堤局部沉降设置,底层土工格栅铺设在水袋盖板以上5 cm位置,中层土工格栅距路堤表面约25 cm,格栅平均厚度约为1 mm,换算抗拉刚度均为388 kN/m,底层格栅长度为3.425 m,中层格栅长度为2.975 m。试验采用方形橡胶水袋安装在填筑路堤底部,安装缝隙处均用细砂填满压实,水袋侧面设泄水阀接流量计。模型稳定后对经沉降标定后分7个阶段对水袋泄水试验,如图2所示。

图2 填筑模型沉降观测与标定Fig.2 Settlement observation and calibration of filling model
1.2 试验结果分析
图3所示为路堤内部土压力的监测结果变化情况,基底差异沉降引起路堤内部应力场改变。受水袋泄水影响,位于基底板之上底层土工格栅以下测得的土压力变化明显,泄水初期Pb-1,Pb-2 与Pb-3 压力相近,随后位于底板中间位置(Pb-2)处的土压力开始减小,两侧土压力(Pb-1 与Pb-3)不断增大。本次试验中,当泄水量超过一定体积即底板沉降达8.0 cm 后,路堤填料与底板间的接触作用明显减弱。水袋泄水产生的基底局部沉降使得沉降槽宽度范围内的路堤填料荷载逐渐转移为由底层土工格栅全部承担,位于沉降槽中间位置监测得到的土压力减至2 kPa 左右,格栅下水袋几无支撑作用。
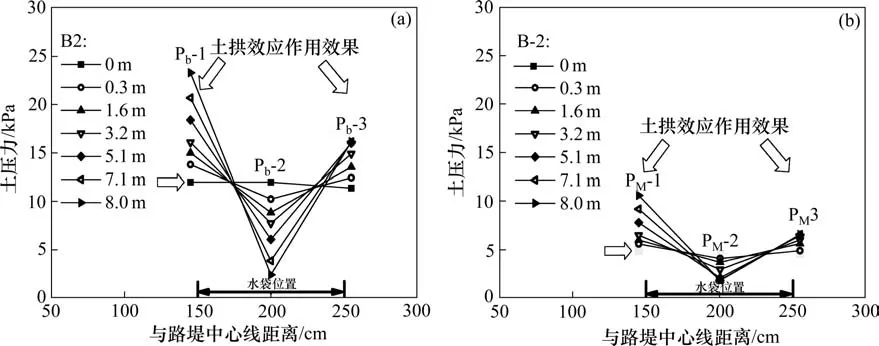
图3 路堤内部土压力变化Fig.3 Stress analysis in the embankment
图4 所示为土工格栅拉伸应变的分布变化情况。底层土工格栅拉应变通长呈马鞍形分布,即沉降槽边沿位置处出现拉应变峰值,中间拉应变稍小;两侧锚固段的格栅拉应变随离开沉降槽距离增加迅速减小。随着水袋的沉降其上覆板对底层土工格栅的支撑力逐渐减小,且接触作用宽度逐渐收窄,即土工格栅在发生挠曲变形后,加筋层仅有很小甚至不受到来自于下部的反力作用,此时两边缘位置产生的拉应变最大。

图4 底层与中层土工格栅轴向拉伸应变Fig.4 Axial tensile strain of the georids
从格栅拉应变的分布变化看,水袋边缘向两侧很短的锚固长度范围拉应变就迅速减小至0,且对应每一级泄水后的基底沉降均是如此,说明在试验设定条件下依靠路堤填料与筋材之间的摩擦力作用,仅锚固有限长度就能够抵消底部筋层在上覆荷载作用下发生挠曲时对两侧的拖拽力;对于中间层土工加筋而言,最大的拉应变却发生在沉降槽的中部,向两侧逐渐递减,呈单峰鼓包型分布。主要原因是由于路堤中部的土工格栅发生挠曲时,其形变过程伴随着上下路堤填料的协同沉降,筋材表面与上下填料之间始终存在着摩擦界面的滑移调整,因此发生的拉应变峰值处于槽宽范围的中间位置。
2 土工加筋工作区段分布模式
在分析水平加筋的薄膜效应时,常规的方法是将挠曲后筋层形变假设为圆形或抛物线形来进行拉应变的分析[20−21],并以均匀的应变常数值为计算目标,且这些方法仅考虑桩净间距范围内的格栅拉伸,对锚固端筋材的作用力贡献考虑较少。然而,VILLARD 等[22]和HAN 等[23]分别从模型试验和数值模拟方法验证了加筋层在沉降槽或桩帽边沿处发生峰值拉应变。而且,通过此次模型试验对不同加筋层位处筋材拉应变的分布规律研究,可判定在加筋层的不同位置其工作性状及受力模式均不同。
图5(a)所示为试验结束后开挖半幅路堤的土工格栅变形情况,很明显土工格栅与上下填料之间的黏结非常紧密,未出现筋土脱离现象。图5(b)所示为基底沉降监测结果,开挖检查与沉降观测结果吻合较好。显然,位于硬地基上的土工加筋基本保持了初始铺设时的状态,但水袋中间位置的土工格栅已发生了明显的下沉凹陷,故认为从硬地基土上的平铺向水袋间的凹陷应有一段弯曲过渡。综合以上分析,认为底层加筋层应采用分区段模式进行受力工作状态分析。

图5 土工格栅挠曲形态模式分析Fig.5 Inspection of the deflected geogrid after testing
根据加筋层受力和变形的特点,参考已有的研究成果[16,25],按图6 进行工作状态模式的划分,从平面应变的角度对其进行受力分析。假设铺设时的土工格栅初始状态由AB段直线表示,当对水袋泄水使基底发生差异沉降后,土工格栅变为曲线A'B'形态,可以将其分为3 段进行受力分析,分别为锚固段、过渡段与挠曲段。锚固段是指硬地基上部分平铺的土工格栅(直线AC段),过渡段即为硬地基边沿土工格栅从水平方向渐变为挠曲形变的弯曲段(曲线CC'段),而纯挠曲段是指底部净跨间距纯挠曲的加筋部分(曲线C'B'段)。其中,弯曲过渡段CC'来自于初始直线段AC的拉伸。

图6 水平铺设的加筋工作模式区段划分Fig.6 Stress analysis of the basal reinforcement
2.1 挠曲段的受力状态分析
参考已有的研究成果[16],为简化加筋层受力分析,作如下假定:1) 将硬地基土的路堤内竖向应力和水袋上地基土内的竖向应力分布都作均值化处理;2) 基于分析模型的对称性考虑,认为理想条件下仅适用于沉降槽宽度范围内挠曲工况,作用在筋层上的均布应力qg产生的作用等效于使抗拉刚度为Jg,跨净间距为b的筋层仅发生了竖直向下为δg的挠曲变形。
如图7(a)所示,假设土工加筋与上下填料的界面接触作用符合库伦摩擦关系,令筋土界面摩擦强度为τmax时的相对位移临界值为u0,为使问题简化暂不考虑筋土界面的黏附力作用(下同)。则某一筋土相对位移条件u下的界面摩擦作用应力强度可表示为:

其中,φ0为筋土界面作用的摩擦角,σn为筋土界面接触作用的法向应力。如图7(b)所示,针对净跨距间的挠曲段,取加筋层在点M处的微元段水平方向长为dx进行受力平衡分析。

图7 位置M处微元段应力状态分析Fig.7 Stress analysis of a element in position M
令筋土上接触面摩擦强度为τu,而筋土下接触面摩擦强度为τl,建立如下关系:

其中,k1为加筋层底部接触界面相对于上部接触界面的折减因子。这主要是考虑到模型中堤底以主动方式实现局部沉降差,弱化了加筋层与下部填料间的作用。
根据图7(b)中对微元段的受力分析,可以建立如下的关系:

又由于qg(x)=qu(x)-ql(x),且ql(x)=ks y(x),则可以得到以下的方程组:

其中,ks是地基土反力系数,y(x)是基底地基土竖向位移。调整后可以得到如下表达式:
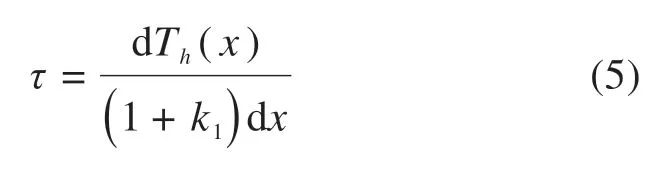
将式(4)中第2个方程两边都除以dx,得到:
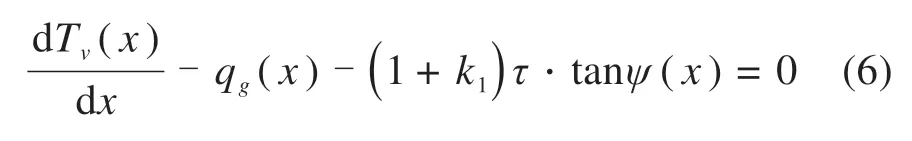
对式(3)中的第2个方程求导得到:
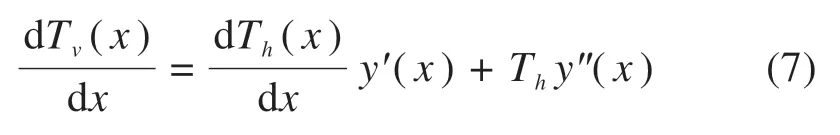
将式(5)和式(7)一起代入式(6)得到:
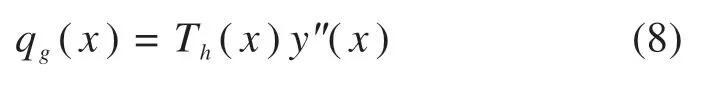
而水平向分力又可以表示成:

其中,Jg=Egt=Tgt/εg,Tg为拉应变εg下的加筋抗拉应力,t为加筋层平均厚度。
同时,也可以得到:
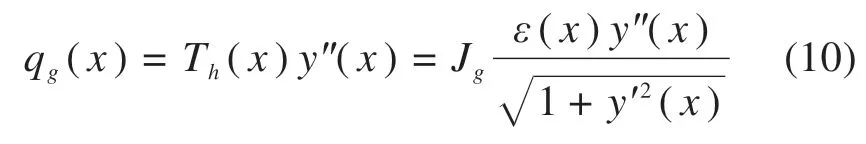
而位置M点位处的格栅拉应变还可表示为:

其中,u表示位于横坐标为x处的土工加筋相对于初始位置的拉伸位移,将式(11)代入式(10)中可以得到:
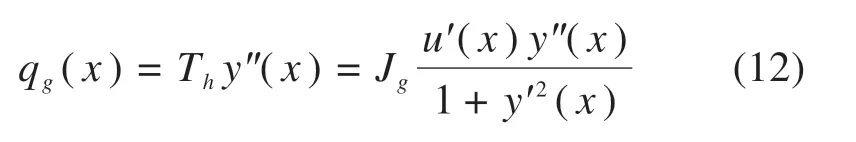
此时,可得到如下关系:

将经土拱效应作用影响下的土工加筋层的上覆荷载均值化为挠曲段范围内竖向应力,可得到:
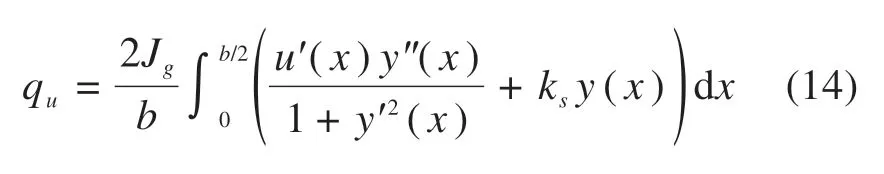
此时,令土工加筋的挠曲形状满足抛物线形或者圆曲线形假设,则可以得到特定挠度下的加筋层轨迹线方程,亦即对应了此时地基土压缩量。
2.2 土工加筋层上覆荷载作用
参考HANDY[24]的摩擦墙理论及在此基础上的理论改进[25],考虑土条单元应力状态受基底位置地基土沉陷的影响,见图8 所示并由应力莫尔圆可知,某位置的应力状态方程如下:

图8 考虑基底沉陷路堤应力状态分析Fig.8 Stress state of the fill due to local subsidece

其中,σh,σv分别为水平向和竖向应力,σ1,σ3分别为大小主应力,θ为大主应力与水平方向的夹角。此时,对应的路堤土中的剪应力为:
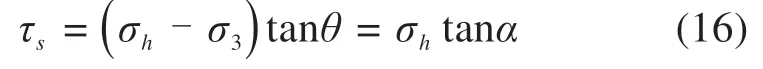
其中,α为剪应力部分发展下的倾角。当Ka=tan2(450-φ/2)时,φ为填料内摩擦角。对应情况下的侧向土压力系数可以表示为:

将式(15)中第一个方程除以σ3代入式(16)得到:
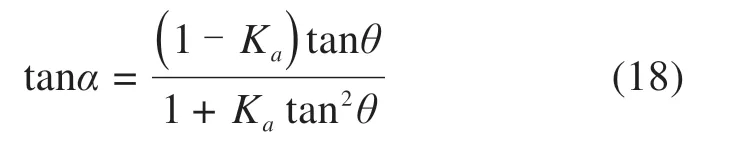
对应路堤中的剪应力式(16)可表示为:
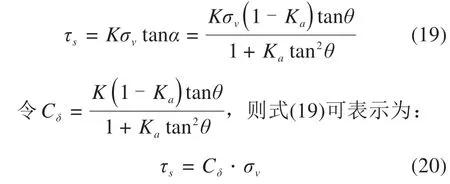
取路堤中的土条单元静力平衡条件有如下关系:
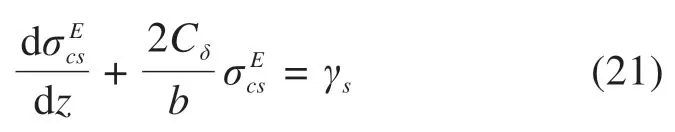
方程(21)的通解形式为:

其中,C1=-γs,则由公式(22)得到路堤底部在沉陷时的路堤填料中的竖向应力可以表示为:
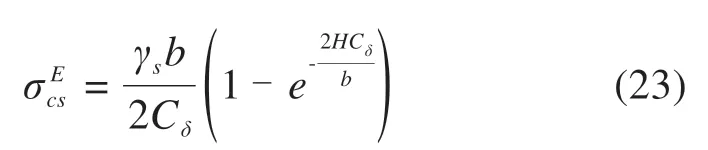
此时,还有如下关系成立:

基于变形协调,路堤底水袋泄水后产生的沉降值可等效为土工加筋的挠度,这也决定了路堤中土拱效应作用下施加在加筋层上的基底应力。
2.3 过渡段等效分析
区别于传统的仅考虑净跨距间土工加筋拉伸应变计算方法以及铺设全长范围内扣除位置点C处位移的处理方式,借鉴VILLARD 等[22]对基底沉降部分与周边硬地基过渡段作圆弧段假设,认为该圆弧段来自于原铺设在硬基上锚固段的拉伸变形,此时有如下关系成立:

其中,ψc为锚固段的C点经拉伸弯曲后到达挠曲段C'点处的切线与水平方向的夹角,而φ0可认为是此处土工加筋与上下填料接触面的综合摩擦角,VILLARD 等[22]认为可取筋层下界面与填料的摩擦角。
基于沉降槽边沿处土工加筋变形协调,考虑图6 中的C点位置即为连接挠曲段与锚固段的过渡区范围内的宏观几何特性,有ψc+θ=π/2 关系成立。
2.4 土工加筋锚固段分析
如图9所示,为考察硬地基上的土工格栅锚固段AC的受力工作状况,认为从硬地基上的某点受拉力作用向右发生拉伸变形,选取距离C点r处的锚固微元段dr进行受力分析,得到:
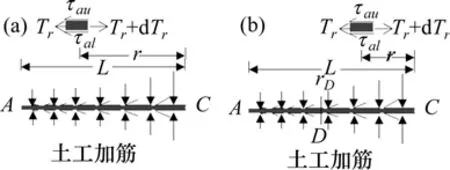
图9 锚固段加筋体水平向受力分析Fig.9 Mechanical analysis of the anchorge section
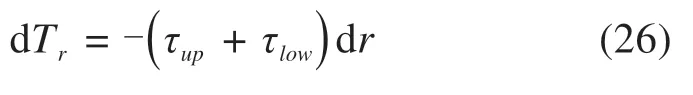
此处,τup,τlow分别为加筋层上下与填料的界面摩擦应力,仅考虑界面筋土之间的摩擦角作用,认为锚固段的筋土界面摩擦关系同样适用库伦摩擦强度关系,则此时在任一筋土相对位移U下的土工加筋与上下填土界面的摩擦应力强度可由下式表示:

其中,σ0表示锚固段加筋层的筋土界面法向应力,可取上覆土重压力;ϕup/low分别为锚固区筋土接触上下界面的摩擦角。则可以得到如下关系:
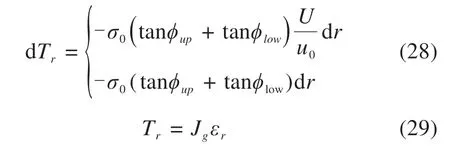
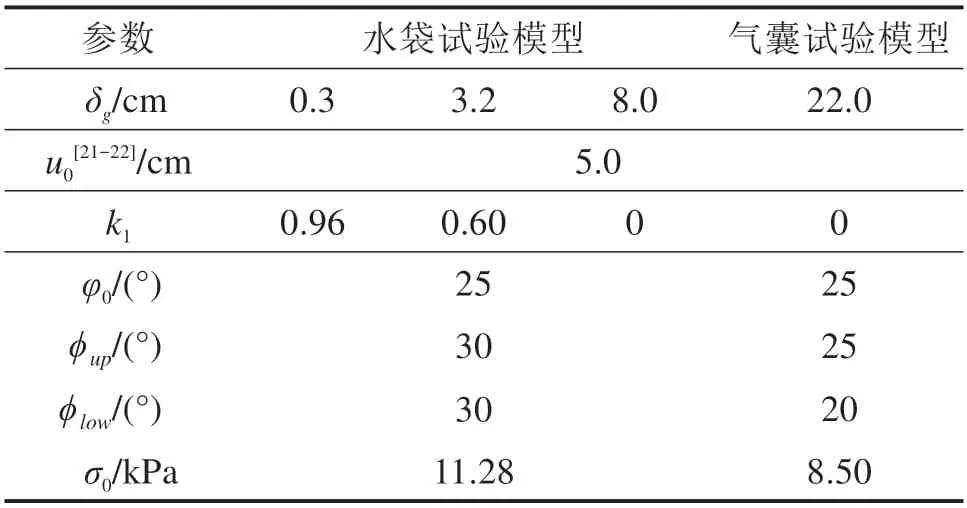
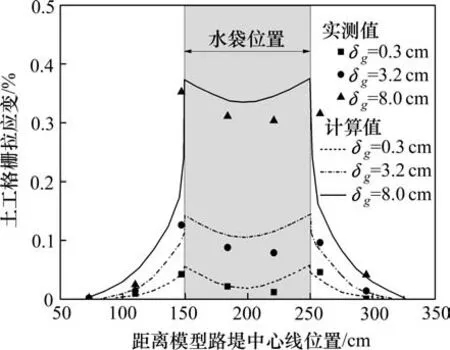
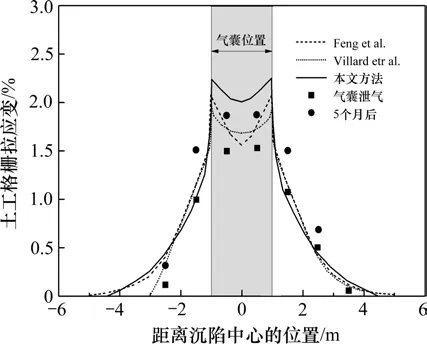
1)当U 将方程(27)~(29)整理得到如下偏微分方程: 其中,β=σ0(tanϕup+tanϕlow)/(Jgu0)。则方程(30)的通解形式为: 其中,C1,C2为取决于边界条件的常系数。当r=L时U=0,当r=0 时T=Tr0。对于任意位置的锚固区加筋拉伸筋土位移可表示为: 土工加筋层在锚固段的拉应力可以由下式表示: 则锚固段位于C点的位移可以表示为: 而对应的临界位移时的拉应力为: 2)当U≥u0时,即为图9(b)工况。 则需要将锚固区的土工加筋工作状态分为2部分考虑,其中的AD段部分为与1)相同情况,采用相同的分析方法与步骤。另一部分CD段有如下关系: 其中,q0=σ0(tanϕup+tanϕlow)。 则可以得到: 对于临界点D位置,有r=rD时T=T0,且U=u0,则对应的临界位置可以求得: 于是,可以建立锚固段邻近沉陷边沿点位移与此处拉应力之间的关系: 若不考虑应力的水平向扩散影响,认为基底加筋作用影响的路堤内部应力重分布仅发生在竖直方向的调整。对于式(12),(22),(35)和(38)中的加筋材料、土的基本物理力学特性和模型几何尺寸等都可以得到明确的参数取值,此时只需知道加筋层中间挠度的最大值δg,式(10)中等效的加筋层均值膜效应qg就可以计算得到。由于土工加筋的存在,当分析模型底部发生向下位移或如水袋泄水产生差异沉降,即相对于周边稳定的土体发生差异沉降,挠曲的加筋层将产生薄膜效应使部分填土荷载转移到邻近处发生应力重分布。基于图5所示开挖检查情况,筋土间的黏接良好,计算筋层拉应变时按竖向应力、位移协调考虑。因此,可按图10对本文推导过程进行迭代求解。 图10 推导过程的计算流程Fig.10 Solution procedures of the proposed method 利用模型试验数据对上述底层加筋层的计算拉应变分析方法进行验证。计算时填土高度取0.6 m,重度为18.8 kN/m3,黏聚力为8 kPa,内摩擦角为24°,沉陷区范围宽度为1.0 m,土工格栅的抗拉强度为388 kN/m。以基底水袋泄水沉降为土工格栅挠度的输入条件,选取3组土工加筋挠度对计算结果与实测结果进行对比,补充计算参数选取见表2所示。在挠曲段范围对加筋上下界面进行定义时,以底板沉降为8 cm 时为最终状态,下界面的折减因子即为某一级与该最终状态比值。 表2 模型试验计算实例相关参数选取Table 2 Selection of parameters in the calculation process 如图11 所示为采用本文方法与模型试验结果的比较。由于计算时将分析模型仅考虑为对称情况,因此得到的拉应变也呈对称分布,这与后续验证实例介绍的另外2种方法相同。很明显,计算结果与实测数据吻合较好,底部沉陷越大,加筋层上覆荷载也越大,得到的筋层拉伸应变越大,这时需要更长的锚固段以兜提该荷载的作用。而且,当土工加筋拉伸强度未充分发挥时,采用本文分析方法也能够得到合理的加筋拉伸应变预测结果。 图11 计算结果与水袋试验模型实测数据对比Fig.11 Composion of tensile strains with water bag model test 为作进一步验证,选用文献[23]开展的通过现场原位对气囊放气实现基底空洞大型试验模型对本文分析方法进行验算。该试验模型填筑路堤高度为0.5 m,重度为17 kN/m3,黏聚力为0,气囊的宽度为2.0 m,高度为0.25 m,气囊上部铺设的单层土工格栅的锚固段长度超过2.0 m,筋层上下界面与填土间的摩擦角分别为30°与25°,筋带极限拉伸应力为125 kN/m 时的拉应变为12%。该试验是用气囊泄气的方式实现基底位移,相对于水袋模型试验,筋层底部支撑会随气囊的泄气瞬间消失,沉陷区路堤土迅速进入临界状态导致土拱效应充分发挥,全部荷载由土工加筋承担且筋层挠度最大值位于中间,因此计算时地基反力设为0。 如图12 所示,气囊泄气试验模型得到的土工格栅拉应变相对较大,且试验结束后的5个月观测得到稳定值更大。针对该模型试验工况,认为本文方法与FENG 方法、VILLARD 方法都能够得到有效的土工加筋拉伸应变的预测结果。只是由于开展试验时监测布拉格光栅的布置在卸门边缘处间隔一定距离,测得的实际土工加筋拉应变分布未反应出在边沿位置处的峰值,仅呈现中间大两边小的分布特点,这与本文的试验结果及所采用的分析方法结果并不矛盾。 图12 气囊试验模型土工加筋拉伸应变对比Fig.12 Composion of tensile strains with the balloon model test 经对比可以发现,本文方法得到的峰值应变偏大,产生这样的结果一方面是因为考虑了挠曲范围筋土的界面摩擦作用(与FENG 方法的处理相类似),另一方面也是由于土拱效应的作用受制于基底沉陷相对位移较小影响其发挥的结果。VIL‐LARD方法在理论假设中不考虑挠曲范围筋土的界面摩擦作用,仅仅考虑上覆土拱效应作用后的上覆荷载作用,因此得到的峰值应变最小,故需要的锚固段长度也最小。 当气囊泄气后,加筋层底部的反力作用完全消除,此时本文方法对挠曲段的下界面以k1=0 进行考虑,这与FENG方法的理论推导前提假设是一致的。本文方法针对沉陷区边沿处土工加筋发生弯曲的过渡段从挠曲段向水平锚固段处所发生的筋带主受力方向的变化的分析,区别于FENG方法采用的是地基土部分压缩筋带拉力转移方法,因此导致2种方法在锚固区的土工加筋拉应变渐变形式上有所不同,前者会存在一个陡变而后者相对较缓和,但基于相似的锚固区力学分析原理所以其区别并不大。 通过以上2个不同实例的比较证明本文所提方法在评判土工加筋拉应变时具有一定的合理性。相比较另外2种方法更适用于筋层底部出现空洞情形,本文方法在评判地基土具有一定反力作用时可以优先选用。但是,该方法是在理想二维条件下开展相应的理论推导,相对应于实际桩承式加筋路堤中仅仅以桩帽尺寸幅宽范围内的加筋工况分析,并没有考虑邻近多排桩之间部分地基土上的土工加筋作用,因此对于双向整体布筋的工况适用性需要拓展研究。 1) 不同层位铺设的土工加筋受力存在明显差异,底层土工格栅存在2个峰值拉应变并分别位于沉降槽两侧边缘,中层加筋仅有单峰值拉应变且位于中间。随着基底沉降差的发展拉应变均不断增长,但位于两侧的筋带锚固段的拉应变均迅速减小直至为零。 2) 进行底层加筋薄膜效应分析时区分不同工作模式以进行受力分析,所提的基于长度范围内锚固段、过渡段和挠曲段假设的分析方法能合理的评判土工加筋的提拉作用,据此给出的筋带非均匀拉伸应变计算方法也得到了实测数据的初步验证。 3) 虽然本文所提的基于工作区段模式区分并部分考虑筋土界面作用的拉应变分析方法被两组试验结果初步验证是合理的,但在原型足尺条件下及双向铺设时的适用性还有待深入探讨并完善,且对于不同土拱效应作用分析下的加筋兜提作用还有待更进一步的研究讨论。

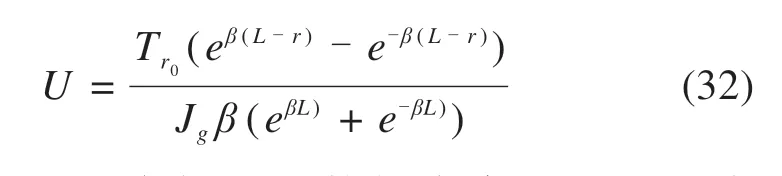
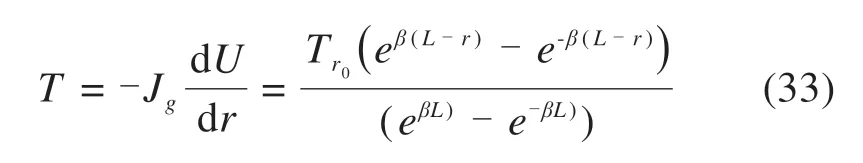






3 迭代求解过程与方法

4 结果验证与分析讨论
5 结论
