一种增加动基座飞行器误差分离结果稳定性的半解析方法

张 青，檀朋硕，傅 瑜，王 勇，林海奇

(北京宇航系统工程研究所，北京 100076)

精度评估一直以来都是各方研究的重点，由于飞行轨迹变化、飞行允许区域限制等约束条件，某些飞行器无法通过试验直接进行精度评估，通常的做法是将各项误差系数通过遥测、外测数据分离出来[1]。与静基座飞行器相比，动基座发射飞行器存在初始误差大、初始误差和工具误差强耦合等特点，其误差分离过程复杂[2]。

目前，中国已经有一些机构对动基座误差分离方法展开了研究。文献[3]建立了视速度域和视位置域下的初始误差分离线性模型；文献[4]将分组遗传算法应用于制导工具系统误差分离；文献[5]提出了一种基于非线性模型的误差估计方法；文献[6]采用经典参数的粒子群算法分离制导工具误差和初始误差；文献[7]提出了一种基于动力系统求解的制导误差分离方法；文献[8]针对发射原点误差对制导工具系统误差分离的影响进行了分析；文献[9]提出了一种地心系下的动基座飞行器制导工具系统误差分离方法。

虽然中国研究机构开展了大量研究，但是在实际工程应用中，由于外测数据存在测量误差，且测量噪声具有较大不确定性，应用上述方法进行动基座误差分离时，分离结果随分离时段和分离项数变化较大，即误差分离结果稳定性较差。针对该问题，现提出一种增加动基座飞行器误差分离结果稳定性的半解析方法，并通过仿真结果验证了方法的有效性。

1 模型建立

1.1 坐标系定义

4种坐标系示意图如图 1所示。

图 1 坐标系示意图Fig.1 Coordinate system

1.1.1 平台质心发射坐标系Of-xyz

坐标原点Of取为平台质心处，y轴与参考椭球体的法线重合指向上方，x轴在过原点的参考椭球体的切平面内指向射击方向，z轴与x轴、y轴成右手正交坐标系。

1.1.2 平台质心发射惯性坐标系Og-xyz

飞行器起飞瞬间，与平台质心发射坐标系Of-xyz重合，飞行器起飞后，坐标系原点Og点及坐标系各轴指向在惯性空间保持不变。

1.1.3 地心惯性坐标系Oc-xcyczc

原点Oc选为地心，xc轴在赤道平面内指向春分点，zc轴与地球赤道平面垂直指向北极，yc轴在赤道平面内，与xc轴、zc轴构成右手正交坐标系。

1.1.4 平台惯性坐标系Op-xpypzp

平台惯性坐标系原点Op在断调平时刻的平台质心，各坐标轴保持惯性器件初始对准后的指向。坐标系Op-xpypzp为惯性坐标系。

1.2 初始定位误差解析求解模型

初始定位误差会同时引起坐标位置差异和指向差异[10]。飞行器理论发射原点Og在地心惯性坐标系内的坐标为

(1)

式(1)中：H0为发射点的大地高程；ξ、η分别为垂线的子午面分量和卯酉面分量，且ξ、η均为小量；e为地球椭球的第一偏心率；Nog为Og点的卯酉圈曲率半径；B0为发射点纬度。

记B0ξ=B0-ξ，且经过近似计算有

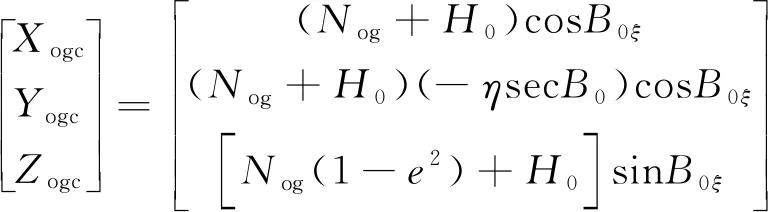
(2)

同理，可以得到飞行器实际发射原点Op在地心惯性坐标系内的坐标为

(3)

式(3)中：ΔH0为发射点的大地高程误差；ΔB0为发射点纬度误差；ΔL0为发射点经度误差；Nop为Op点的卯酉圈曲率半径。

飞行器理论发射原点Og与实际发射原点Op的位置差在地心惯性坐标系内可以表示为

(4)

其中，卯酉圈曲率半径计算公式[11]为

(5)

式(5)中：a为地球半长轴。

将式(5)代入式(4)，并进行简化，可得

(6)

式(6)中：

将地心惯性坐标系中的位置转换到发射惯性坐标系中，则有

(7)

式(7)中：Xogg、Yogg、Zogg为理论发射点在发射惯性坐标系，可以通过遥测参数获得；Xopg、Yopg、Zopg为实际发射点在发射惯性坐标系，可以通过外测参数获得；V为地心惯性坐标系到发射惯性坐标系的转换矩阵[11]。

由于在工程实践中，难以通过外测直接得到动基座飞行器发射点参数，需要通过飞行初段视位置差解算得到发射点位置差。即

ΔgOg-p=Yyc(t)-Ywc(t)-ΔYΔW(t)

(8)

式(8)中：Yyc(t)为t时刻遥测视位置；Ywc(t)为t时刻外测视位置；ΔYΔW(t)为t时刻由遥外测视速度差引起的视位置差，即

(9)

飞行初段遥外测视速度误差较小时，可以忽略由遥外测视速度误差引起的视位置误差，此时有

ΔgOg-p=Yyc(t)-Ywc(t)

(10)

另外，为了减小外测测量误差对初始定位误差分离结果的影响，可以选取一段时间的遥外测视位置参数进行计算。

将式(10)代入式(7)，则有

(11)

求解式(11)可以得到初始定位误差的解析解为

(12)

1.3 初始速度误差解析求解模型

遥外测视速度差主要包括初始定位误差、初始速度误差、初始对准误差和惯性系统工具误差，即

ΔWg(t)=Wgyc(t)-Wgwc(t)=

ΔWcsd(t)+ΔWcsv(t)+ΔWcsz(t)+ΔWgj(t)

(13)

式(13)中：Wgyc(t)为t时刻的发射惯性坐标系下遥测视速度；Wgwc(t)为t时刻的发射惯性坐标系下外测视速度；ΔWcsd(t)为t时刻初始定位误差引起的遥外测视速度差；ΔWcsv(t)为t时刻初始速度误差引起的遥外测视速度差；ΔWcsz(t)为t时刻初始对准误差引起的遥外测视速度差；ΔWgj(t)为t时刻惯性系统工具误差引起的遥外测视速度差。

外测数据一般为发射坐标系下的速度参数，需要通过转换计算得到发射惯性系下的外测视速度参数，即

(14)

将式(14)代入式(13)，有

ΔWcsd(t)+ΔWcsv(t)+ΔWcsz(t)+ΔWgj(t)

(15)

根据文献[1]可以计算得到初始定位误差对遥外测视速度差的影响；根据文献[12]可以计算得到初始对准误差和惯性系统工具误差对遥外测视速度差的影响。则初始速度误差求解公式为

ΔWcsz(t)-ΔWgj(t)

(16)

需要指出的是，飞行初段初始速度误差对遥外测视速度差的影响较其他误差更为显著，因此采用飞行初段分离得到的初始速度误差更接近于真实值。

与初始定位误差分离相同，为了减小外测测量误差对初始速度误差分离结果的影响，可以选取一段时间的遥外测参数进行计算。

1.4 初始对准误差和惯性系统工具误差的Bayes估计

初始对准误差引起惯性基准漂移，在受到视速度激励后，引起遥外测视速度差和视位置差。由于初始对准误差的影响机理和作用效果与部分惯性系统工具误差相近，因此可以一起进行参数估计。

根据式(13)，发射惯性坐标系下，初始对准误差和惯性系统工具误差引起的遥外测视速度差为

ΔWcsz(t)+ΔWgj(t)=ΔWg(t)-ΔWcsd(t)-ΔWcsv(t)

(17)

按照环境函数法，建立的误差分离模型为

ΔWzgj=ΔWg-ΔWcsd-ΔWcsv=SC+ε

(18)

式(18)中：ΔWzgj为初始对准误差和惯性系统工具误差引起的遥外测视速度差；S为环境函数[12]；C为误差系数；ε为观测误差矢量。

利用Bayes参数估计方法，对误差系数进行估计，估值模型为

(19)

式(19)中：C0为误差系数验前期望值；K为协方差矩阵[13]；PC0为验前方差阵，即

(20)

由于初始对准误差和惯性系统工具误差，在受到时间、视速度、视加速度的激励后，引起遥外测视速度差，且其对遥外测视速度差的影响与所受激励成正比，因此采用飞行中段及后段参数进行误差分离，分离结果更加接近真实值。

2 半解析方法

影响动基座飞行器精度的误差源主要包括：初始定位误差、初始速度误差、初始对准误差和惯性系统工具误差。从误差影响机理分析，初始定位误差直接引起遥外测视位置差，初始速度误差直接引起遥外测视速度差，初始对准误差和惯性系统工具误差在受到视速度、视加速度的激励后引起遥外测视速度差。

因此，在误差分离时，利用飞行初段的遥外测视位置差，通过解析方法可以求解得到初始定位误差；利用飞行初段的遥外测视速度差，通过解析方法可以求解得到初始速度误差；利用飞行中段及后段的遥外测视速度差，通过Bayes方法估计得到初始对准误差和惯性系统工具误差。另外，考虑到误差耦合影响，可以采用迭代方法进一步提高误差估计的精度和稳定性。

动基座误差分离流程如图 2所示。

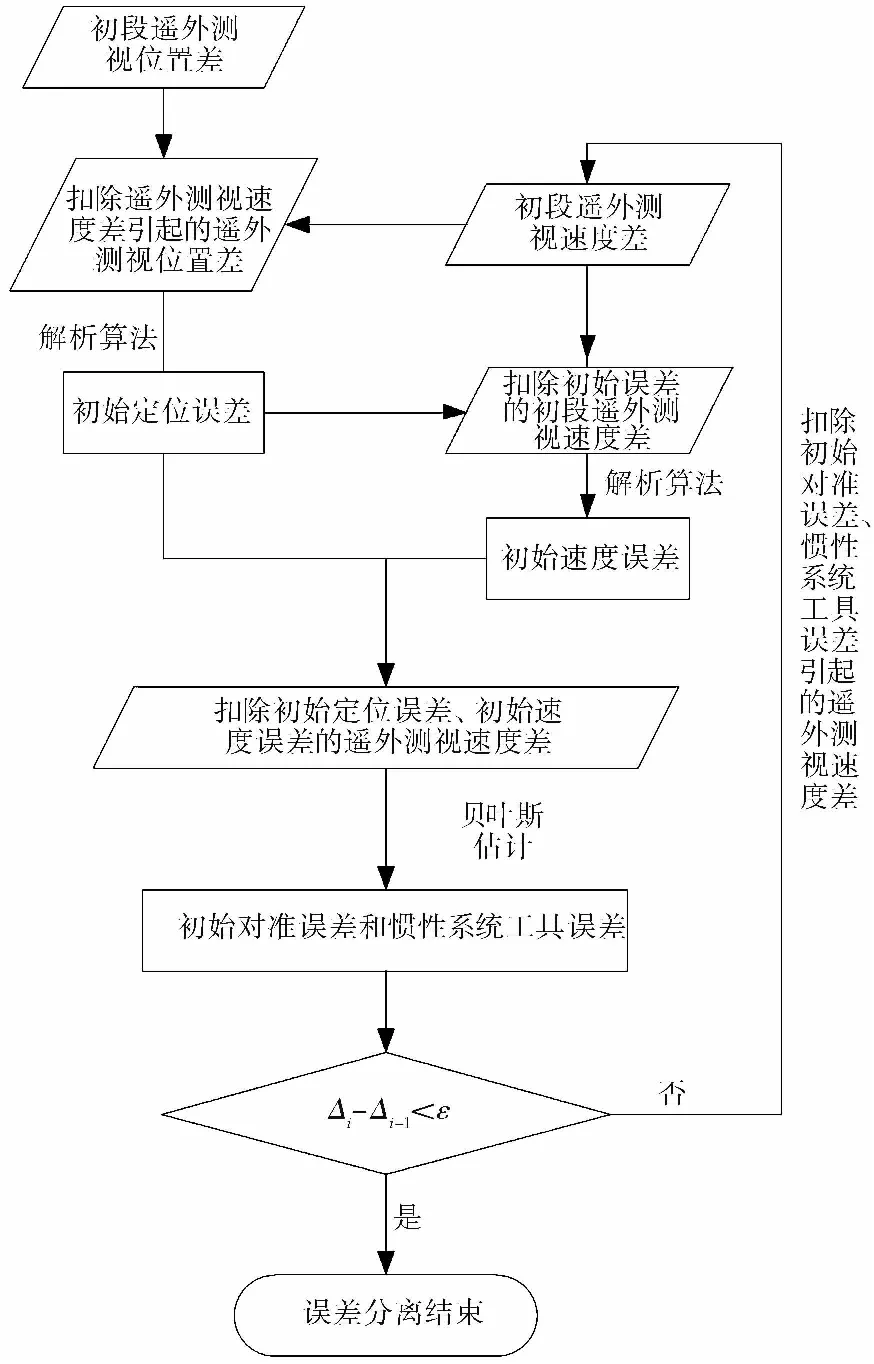
图 2 误差分离流程示意图Fig.2 Process of error separation

3 仿真算例

设计了仿真算例进一步说明方法有效性。仿真条件如下：①考虑3项初始定位误差、3项初始速度误差和3项初始对准误差；②考虑24项惯性系统工具误差。基于文献[12]提到的平台单星复合制导误差模型，分别采用文献[3]中提到的分时段误差分离方法和提出的半解析方法进行误差分离。结果分别如表 1、表 2和图 3所示。

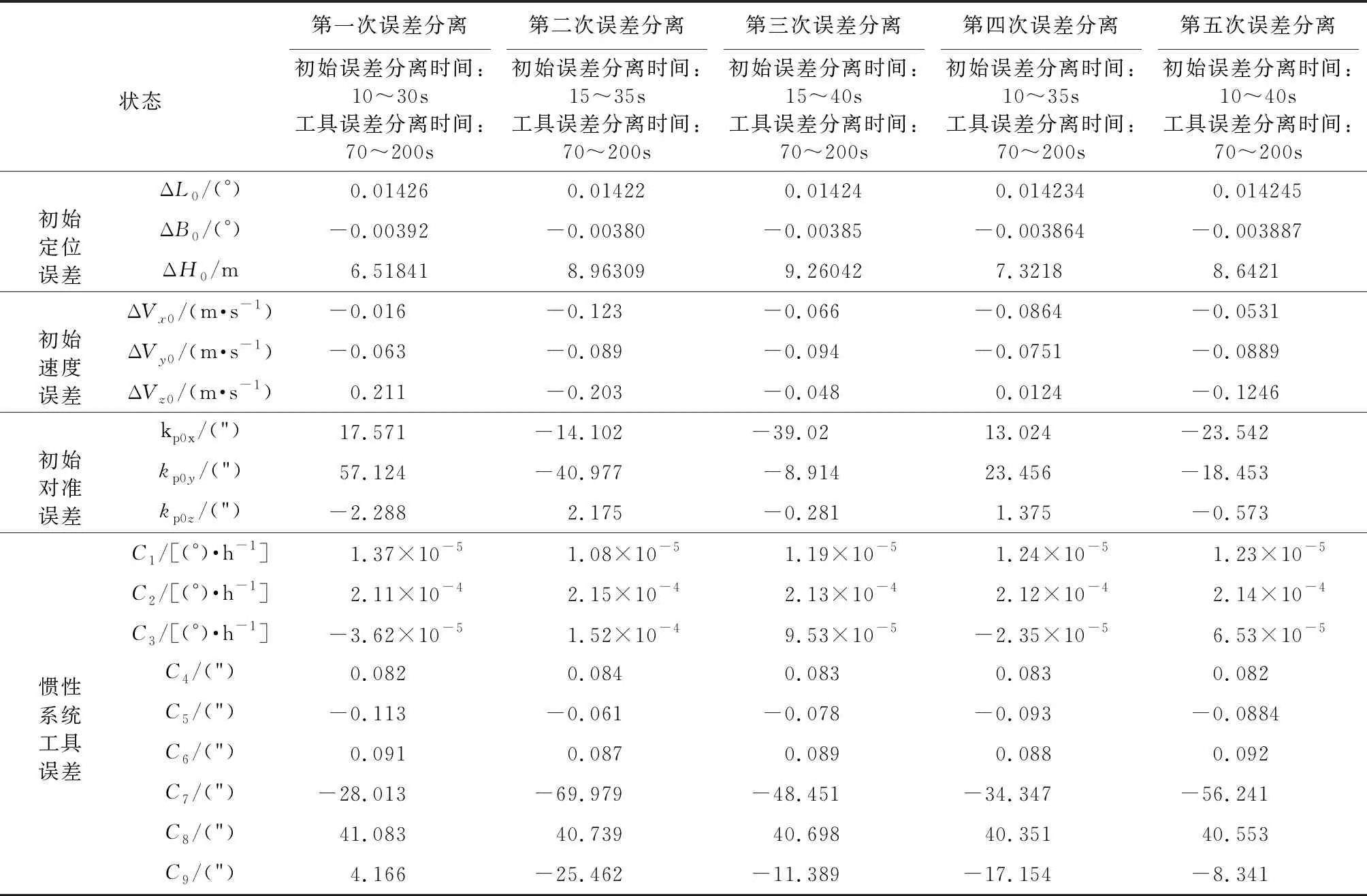
表 1 分时段误差分离方法Table1 Time division error separation method

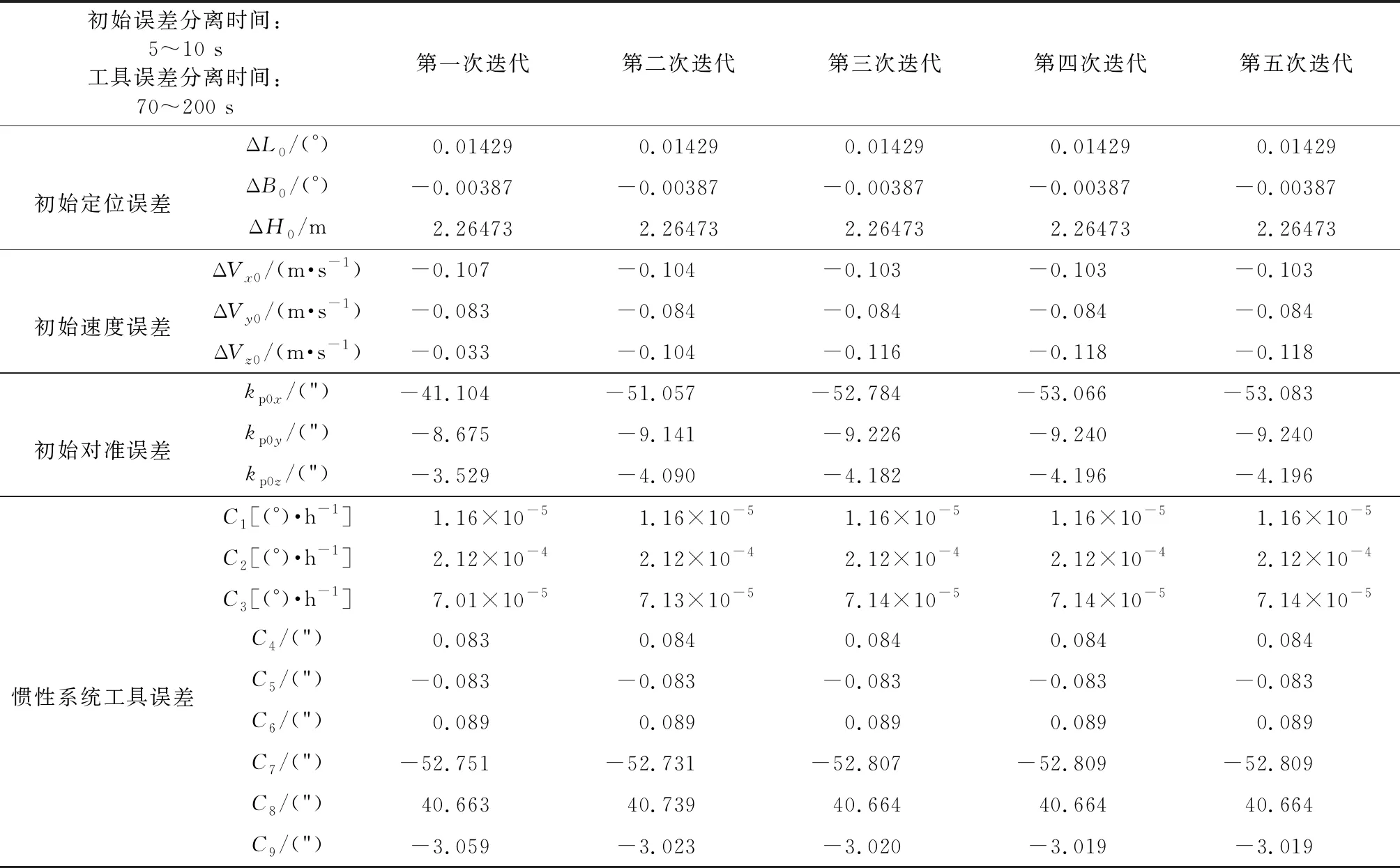
表 2 半解析误差分离方法Table2 Semi-analytical error separation method

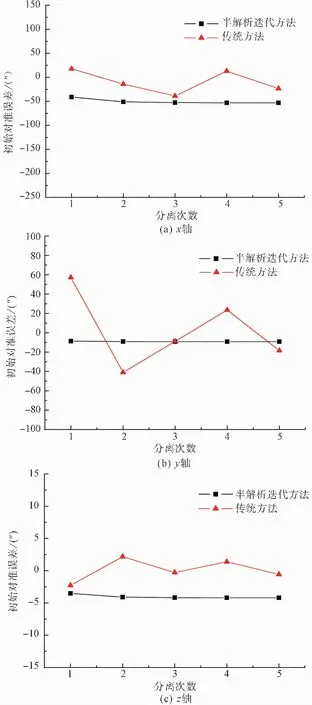
图 3 初始对准误差分离结果对比图Fig.3 Comparison of separation result for initial alignment error

从表 1结果可以看到，采用分时段误差分离方法时，误差分离结果具有较大的不确定性。造成该结果的主要原因在于：分时段误差分离方法下，需要利用飞行初段遥外测位置差同时分离初始定位误差、初始速度误差和初始对准误差，而初始速度误差对遥外测视位置差的影响需要经过时间累计，初始对准误差需要在视速度激励后产生遥外测视速度差，再经过时间累计才能影响遥外测视位置差。因此，采用分时段误差分离方法时，初始误差分离所选时间不宜太短，否则飞行时间短，视速度小，激励出的初始速度误差和初始对准误差小，分离结果受外测数据测量噪声影响大。但是若所选分离时间太长，飞行时间长，视速度大，激励出的惯性系统工具误差将较大，工具误差与初始误差严重耦合，也无法进行有效分离。因此，初始误差分离所选时间直接影响误差分离结果，误差分离结果稳定性较差。

表 2中给出了由半解析方法得到的误差分离结果，经过5次迭代，误差分离结果收敛。半解析方法能够获得稳定分离结果的主要原因在于：半解析方法采用遥外测视位置差分离初始定位误差，采用遥外测视速度差分离初始速度误差，观测数据与误差量对应，直接采用解析方法求解，分离结果稳定；半解析方法下，初始定位误差、初始速度误差和初始对准误差分别求解，针对不同误差特点选择观测量和分离时间，改善分离结果稳定性；采用飞行初段数据代替某单点数据进行求解，减小测量误差影响；采用迭代方法求解，进一步提高了分离结果的精度和稳定性。

4 结论

动基座飞行器误差分离存在初始误差与工具误差强耦合的问题，传统方法利用遥外测视速度进行求解，受测量噪声影响大，误差分离结果不稳定。通过对初始定位误差和初始速度误差进行机理分析，建立了解析求解模型，同时考虑制导工具误差进行迭代求解。算例仿真分析表明，采用半解析误差分离方法得到的误差分离结果受分离时段影响较小，有效提升了动基座飞行器误差分离结果的稳定性，达到了预期效果。在此基础上，后续将进一步研究动基座飞行器误差分离准确性的评价方法。