军用飞机最大故障速度计算

郑峰敏，安 彦

（航空工业西安飞机工业（集团）有限责任公司西飞设计院，西安 710089）

军用飞机最大故障速度是飞行员基于飞行训练实际需求和安全考虑人为规定的。目前，国内军用、民用等其他相关标准[1-2]未对该速度进行阐述和定义，相关研究[3-7]也只是针对临界发动机故障后的相关性能进行展开。基于此，以某型军用飞机为例，从飞机地面动力学建模入手，结合飞机的防滑刹车系统设计，对飞机的加速滑跑段、刹车停止段进行动力学仿真计算，全面分析飞机不同运动状态下的动态响应特性，对飞机最大故障速度展开研究，对指导部队训练和提高飞机起飞安全系数具有重要意义。

1 最大故障速度

故障速度VEF是飞机在起飞滑跑过程中，当飞机出现发动机失效以外的故障时，飞行员进行中止飞行操作时的速度。若飞机从起飞到停止整个过程所滑跑距离（中止起飞距离S）恰好等于机场跑道长度SR，此时对应的速度为最大故障速度VEFmax。

飞行员在故障速度VEF处（中断点）开始刹车，全部发动机推力减小至慢车状态。整个飞行过程可分为两个阶段：加速段和减速段，模型简图如图1所示。

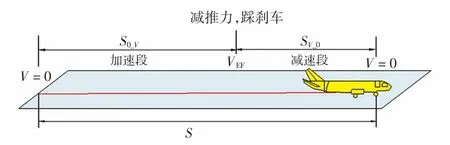
图1 飞机中止起飞简图Fig.1 Sketch of aircraft takeoff abortion

2 飞机运动仿真模型

飞机起飞滑跑阶段需考虑外部环境因素（气动力、跑道状况等）、飞机系统（发动机推力、刹车系统）与飞机本身之间的相互作用，综合考察飞机在滑跑时的动态特性[8]。

飞机抬前轮前后两阶段所考虑的飞行侧重点不同，除飞行姿态以外，速度、迎角、抬轮速率及升、阻力系数也不相同[7-8]。但飞机滑跑及抬前轮阶段的计算模型[6]是相同的。飞机水平和垂直方向运动方程为

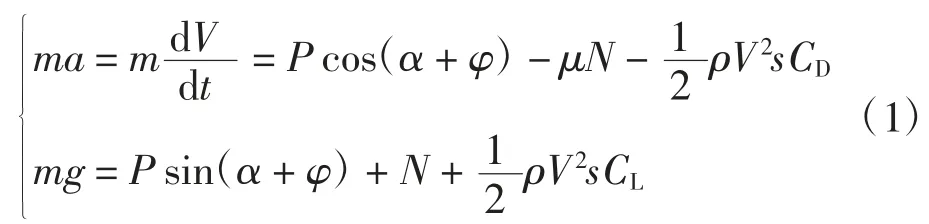
式中：m为飞机质量；a为水平加速度；g为重力加速度；V为滑跑时的瞬时真空速；t为时间；P为发动机的实际瞬时推力；α 为飞行迎角；φ 为发动机安装角；μ 为机轮与地面的摩擦系数；N为地面支撑力；ρ 为密度；s为机翼面积；CL、CD分别为升力系数和阻力系数。

中止起飞距离[4]计算公式为

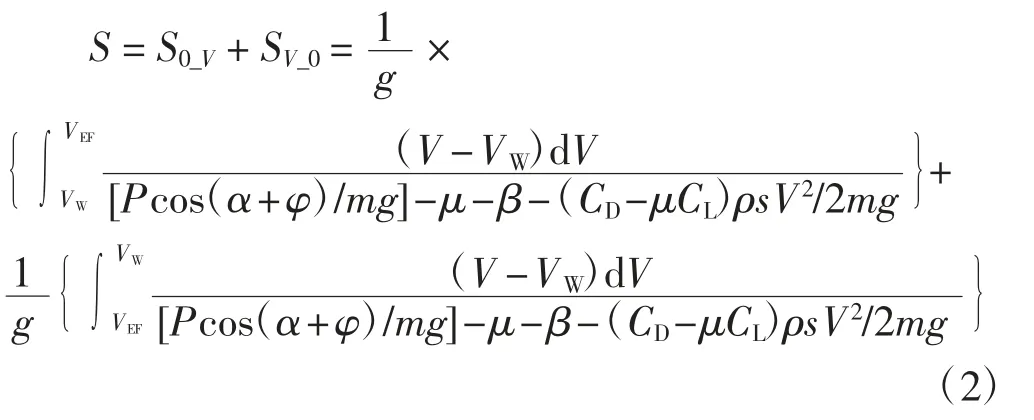
式中：S0_V为从开始滑跑到中断点的距离（加速段距离）；SV_0为从中断点到停止的距离（减速段距离）；VW为风速（逆风取正，顺风取负）；β 为跑道平均纵坡（逆坡取正，顺坡取负）。

计算中止起飞距离时，其防滑刹车模型的准确性是影响计算精度的关键因素之一。防滑刹车模型中的滚动摩擦系数使用等效值，刹车时摩擦系数与地速、胎压、防滑效率和防滑装置有关，可由插值矩阵得出。

3 中止起飞计算模型及方程求解

3.1 算法思路

飞机以全发起飞推力从速度为0 时开始加速运动，在最大故障速度VEFmax时中止起飞，VEFmax可能比给定的抬前轮速度VR小，也可能比其大，可分以下两种情况：当VEFmax≤VR时，飞机在VEFmax时减小推力并开启刹车，即使到达了给定的VR也不会抬前轮；当VEFmax＞VR大时，飞机先到达VR，给定迎角变化率，模拟抬前轮过程，速度达到VEFmax时开始减小推力，以该时刻的迎角作为基准，给定3 s 后飞机迎角减为0，并在此时开启刹车。

当飞机速度减为0 时，比较中止起飞距离与给定机场跑道长度SR。如果长度不等，则调整VEFmax大小，使中止起飞距离等于给定机场跑道长度SR。

建立VEFmax计算模型，需要结合全发正常起飞计算模型[6]，调用其中的地面最小操纵速度VMCG和离地速度VLOF作为VEFmax的判定条件。VEFmax需满足：VMCG≤VEFmax≤VLOF。

3.2 计算模型

以上述算法为基础，建立中止起飞计算模型。根据具体机型实际飞行的操作特点，并结合起落架、刹车、发动机及气动模型等模块，基于Visual C++编写计算仿真程序，程序流程图如图2所示，将程序分为多个功能模块，模块间存在调用与被调用的关系。

图2 中止起飞过程计算模型Fig.2 Calculation model of takeoff abortion process

3.3 微分方程求解及迭代计算过程

微分方程求解采用4 阶Runge-kutta 法[9-10]。方程组中的状态变量一般为非线性函数，难以得到解析解，因此，采用数值分析方法求解。给定初始条件和操作规律后，通过数值法求解非线性微分方程组，可解出每时刻下的若干飞行运动状态参数。

由于建立的数学模型中变量较多，且数量级差别较大，根据工程经验选择以定步长与变步长相结合的迭代方式，可节省计算时间，提高计算精度和准确度。通过定步长数值积分后的距离大小判断是否需要继续迭代，通过局部截断误差大小判断是否需要改变计算步长，从而进行有效迭代计算。

假定三点滑跑段的机身迎角一定，不随时间变化；抬前轮段机身迎角变化率一定，不随时间变化。通过气动数据库计算CL、CD从而得到升、阻力，利用刹车模型及发动机模型三维插值得到μ、P，襟翼为起飞襟翼，放起落架。根据动力学方程得到a、速度增量ΔV、距离增量ΔS等参数。通过给定时间步长Δt，计算下一时刻速度、加速度、距离等参数，依次迭代，依照模型计算流程对结果进行判定，从而得到最大故障速度值。

假定每一Δt内的加速度为常数，则中止起飞距离计算如下

t时刻下每段距离增量可按以下两种方式计算，即

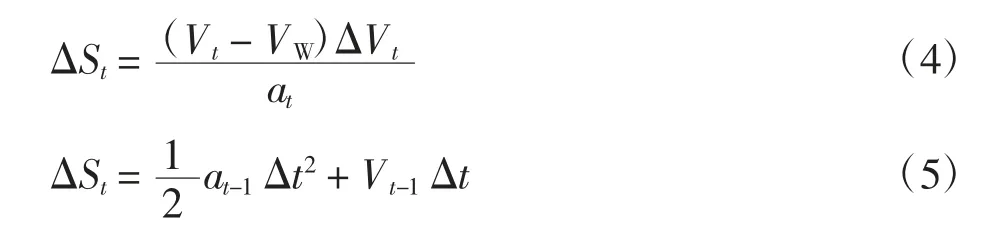
中止起飞加速段距离和全发制动段距离都可以用该迭代方法求得。

4 算例分析

4.1 最大故障速度计算

选取某型飞机常用的3 种飞机重量（G1＜G2＜G3）、3 个机场标准高度（H1＜H2＜H3）、3 个机场温度（T1＜T2＜T3），通过算例来计算某型机最大故障速度，结果如图3～图5所示。

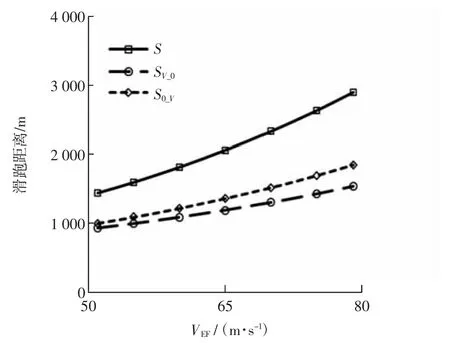
图3 滑跑距离随VEF 的变化曲线Fig.3 Running distance vs.VEF

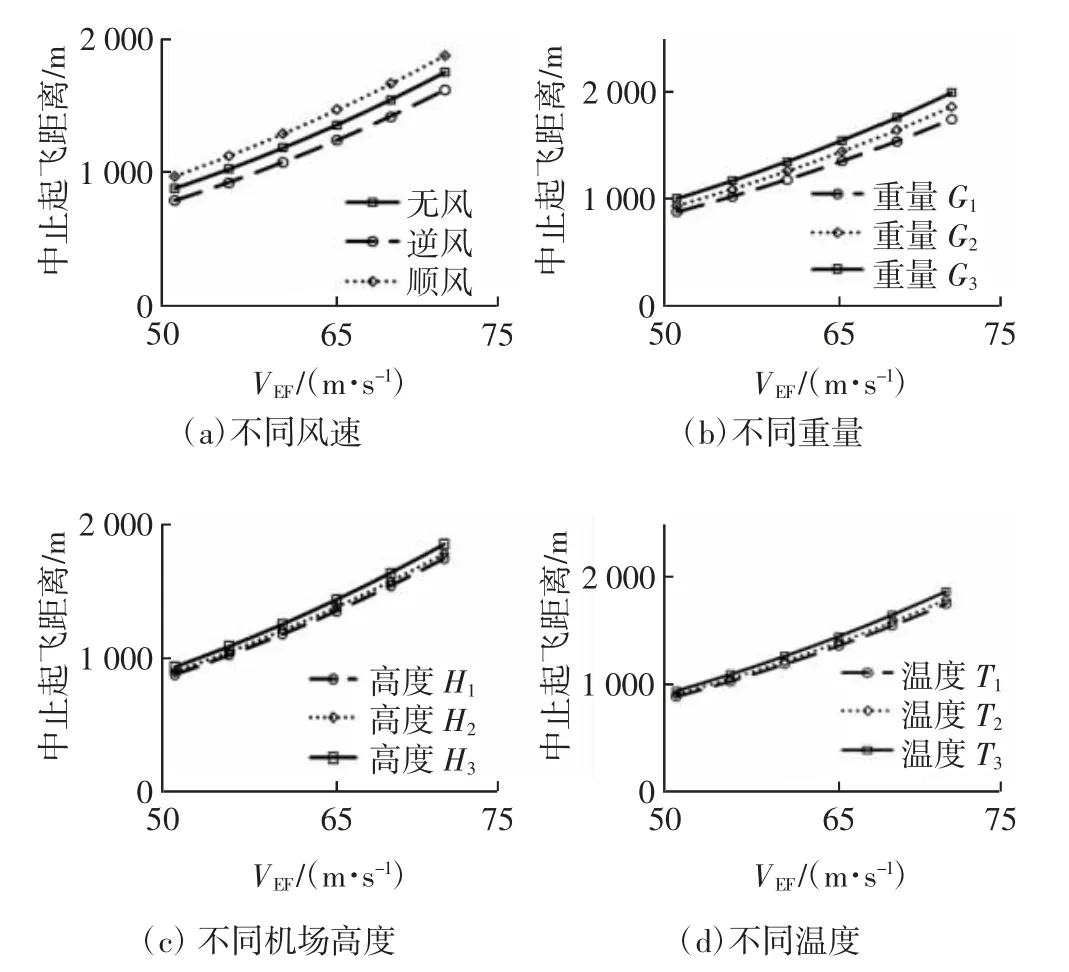
图4 不同条件下中止起飞距离随VEF 的变化曲线Fig.4 Aborted take-off distance vs.VEF under different conditions

图5 速度随重量变化曲线图Fig.5 Speed vs.weight

图3 给出计算过程中滑跑距离随故障速度的变化曲线，可看出：随着故障速度增大，S0_V、SV_0及S均增大；呈非线性变化，速度越大，变化越剧烈；S0_V始终大于SV_0。

图4（a）给出不同风速下中止起飞距离随VEF的变化曲线图，可看出：不同风速下的中止起飞距离均随VEF增大而增大；逆风时中止起飞距离最小，而顺风时中止起飞距离最大，可见逆风对中止飞行有利。从图4（b）～图4（d）可看出，同一VEF时，飞机重量越大、机场高度越高、外界温度越高，则对应的中止起飞距离越长。当速度一定时，重量越大，推力不变的情况下，需要更长的滑跑距离才能使飞机停下来；飞机起飞推力随着机场高度和外界温度的增高而降低，重量不变的情况下，推力不足以使飞机在短距离停下来，故需要更长的距离。而同一中止起飞距离时，重量越大、机场气压高度越高、外界温度越高，则对应的VEF则越小，因此，当机场跑道长度确定时，要使飞机在跑道上安全停下来，则需要减小VEF。

图5 给出了VR与VEFmax随重量的变化趋势：小重量时VEFmax＞VR；随着重量增大，VEFmax逐渐减小，直到某一重量下两者相等；重量继续增大，则VEFmax＜VR。对于确定的机场，均存在某一重量G0：当起飞重量≥G0时，VEFmax≤VR，飞机可在抬前轮之前安全刹车停止。当起飞重量＜G0时，VEFmax＞VR。程序设定在VEFmax时减小推力，3 s 后飞机迎角减为0，并开启刹车停车，保证飞行安全。

假定某型机某重量下VR=65 m/s，当VEFmax=66 m/s时，程序迭代计算3 s 后速度为70.9 m/s，此时飞机机身迎角为0，加速度为0，且该速度应满足：VLOF≥VEFmax，程序设定基本符合飞行员实际操作习惯。

4.2 临界发动机故障速度对比

某型机参考文献[1]计算飞机临界发动机失效特性，如图6所示，其中，A为单发失效停止距离与单发失效起飞距离的交点，此时对应的速度为决断速度V1（临界发动机失效后2～3 s 后的速度），对应的距离为临界机场长度L。B、C为在固定机场长度L1、L2时对应的最大故障速度点。

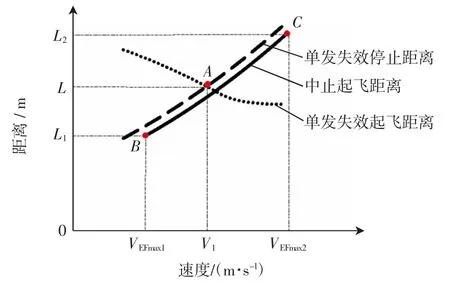
图6 临界发动机故障速度与最大故障速度对比Fig.6 Comparison between critical engine failure speed and maximum failure speed

由图6所示，若飞机重量、场温、场高给定，则临界发动机失效速度是定值，飞机最大故障速度可能等于该值，如A点，也可能小于或大于该值，如B点、C点。以文献[1]计算的临界发动机失效速度未考虑实际的机场跑道长度，故以此速度来判定飞机起飞是否安全意义不大。而最大故障速度则是以具体机场长度为标准，当飞机发生发动机失效以外的故障时，飞行员均可在最大故障速度之前将飞机安全停下来。这也从侧面体现了该计算原理，如只考虑飞行员人为中止起飞后飞机可以安全停下，不考虑继续起飞，则计算裕度可以延长到跑道端头。同时，在同一VEF下，单发失效停止距离要大于中止起飞距离，是由于单发失效和人为关车两种状态下发动机推力衰减规律不同导致的。

4.3 试飞数据对比

某型机选择某一机场、某一起飞重量下进行试飞验证，任务过程及相关操作如下：起飞襟翼，发动机全发起飞状态，飞机沿跑道加速至VEF后，发动机油门收至慢车，柔和踩刹车到底，迅速放襟翼至着陆襟翼，继续减速至飞机完全停止。

因无法直接读取全过程滑跑距离长度，通过对飞机飞行起、止位置的经纬度测量，给出最终的中止起飞距离。为保证飞行安全，最大故障速度的试飞测量采用多次试飞、速度由小到大、飞机逐渐逼近跑道端头、滑跑距离逐渐接近机场跑道长度的试飞方式。试飞情况如图7所示，先小速度试飞，然后逐渐增大VEF，直到S等于机场跑道长度SR，此时速度即为VEFmax。

图7 随速度变化的试飞情况Fig.7 Flight test mode vs.speed

将仿真计算结果与实际试飞数据进行比较，验证该算法的正确性和适用性。取某型飞机在相同状态下3 次有效架次数据进行验证，数据如表1所示。

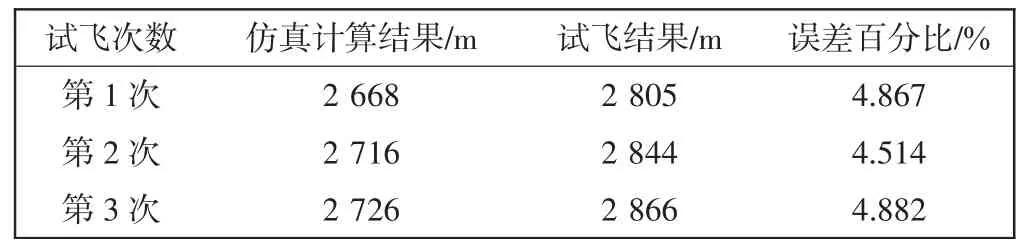
表1 仿真计算结果与试飞结果对比Tab.1 Simulation results vs.test flight results

由表1 可以看出，仿真计算结果与实际试飞结果相比，仿真结果均小于试飞结果，误差范围在5%以内。由于人为操作与仿真计算存在差异，加之机场跑道表面质量、风速、风向等不确定因素，仿真计算结果难以做到与实际情况完全一致。仿真结果误差较小，在可接受范围内，表明该仿真模型正确，计算结果可信，可为部队实际训练提供参考。

5 结语

通过分析计算原理，建立仿真模型及运算程序，并结合实际算例及试飞数据分析可知，最大故障速度仿真计算方法正确可行。机场跑道长度一定时，最大故障速度受起飞重量、机场气压高度、外界温度、风等因素的影响。由于民航和国家军用标准等相关标准都未对该速度做出规定，该速度的定义和计算方法是在与飞行人员沟通交流并在征得飞机设计人员一致认可的情况下而设定的，具有重要的实际意义和适用性。该计算方法可在部队进行推广，并作为部队试飞训练的参考，保障实际飞行安全。