基于深度强化学习的巡飞弹突防控制决策

高昂，董志明，叶红兵，宋敬华，郭齐胜

(1.陆军装甲兵学院 演训中心，北京 100072；2.湘南学院，湖南 郴州 423099)

0 引言

按照全域机动，全域力量投送，创造领域优势，确保行动自由的“多域战”作战理念，巡飞弹这种飞航式智能弹药成为军事领域的重要发展方向[1-3]。巡飞弹如何在动态对抗环境中有效规避威胁、提高生存力是其执行作战任务成功与否的关键[4-5]。目前，巡飞弹航迹规划方法主要分为基于知识、推理、规划，仿生优化，学习3类方法[6]。第1类方法缺乏探索及发现框架之外新知识能力；第2类方法适用于求解旅行商这类静态环境下的路径规划问题，难以应用于动态对抗、决策实时性要求较高的环境；深度强化学习(DRL)属于第3类方法，DRL可以突破专家先验知识的限制，直接从高维战场空间中感知信息，并通过与环境不断交互优化模型。目前，采用DRL方法进行飞行器航迹规划的工作并不多。文献[7]在航迹终端约束条件下，基于DRL实现无人机从终端附近任意位置向目标点自主机动；文献[8]在城市环境中，基于DRL实现无人机从静态障碍物中通过，并到达指定目标区域。尽管飞行器控制在自主化方面已经取得了一定进展，但上述方法仍需要在更复杂的环境下进行进一步测试，例如动态环境中的航迹规划对飞行器来说仍然具有挑战性。本文考虑了存在潜在敌人威胁条件下，飞行器自主航迹规划问题，其难点在于飞行器在完成任务之前，并不知道威胁的数量、位置、策略，因此，必须学习一个合适的策略来对动态环境做出反应。具体来说，假设敌人的地空导弹雷达能够探测到一定范围内的巡飞弹，并能够影响巡飞弹在一定空间内的生存概率，因此巡飞弹必须学会在保证其自身不被摧毁的前提下完成突防任务。

1 基于马尔可夫决策过程的巡飞弹突防控制决策模型

巡飞弹的作战运用方式为，当其收到控制平台发出的敌目标信息后，会绕过威胁区域，选择高效飞行搜寻路线，对固定目标实施打击。本节将巡飞弹机动突防建模为马尔可夫决策过程(MDP)，建立巡飞弹飞行运动模型，设计巡飞弹状态空间、动作空间、奖励函数。MDP可由元组(S,A,P,R,γ)描述，S表示有限状态集；A表示有限动作集；P=P(st+1|st,a)表示状态st下，采取动作a后，转移到下一状态st+1的概率，t为仿真时间；巡飞弹在与环境交互过程中，在每个时间步长内，根据状态st执行动作a，通过与环境交互，生成下一时间步长的状态st+1；R(s,a)表示状态s下采取动作a获得的累积奖励，r(s,a)表示状态s下采取动作a获得的即时奖励；γ为折扣因子，用来计算累积奖励E.定义状态值函数vπ(s)和状态- 行为值函数qπ(s,a)分别如(1)式和(2)式。

(1)

式中：k为仿真时间间隔；vπ(s)能够衡量策略π下状态s有多好。相应地，状态- 行为值函数定义为

(2)

由上述可以看出，qπ(s,a)衡量的是采用策略π时，在状态s下采取动作a有多好。

1.1 巡飞弹飞行运动模型

巡飞弹的空间质心运动采用3自由度质点运动模型[9-10]，假设巡飞弹发动机推力和速度方向一致，采用北东地大地坐标系，建立巡飞弹质点动力学运动模型fm(t)如(3)式所示，系统转移概率P(·|s,a)=1.

(3)

式中：x、y、z表示大地坐标系下坐标分量；v表示速度矢量；vx、vy、vz分别表示巡飞弹在x轴、y轴、z轴3个方向的分量速度；g表示重力加速度；β、φ、φ分别表示航迹倾角、航向角、滚转角；nx、nz分别表示巡飞弹切向过载和法向过载。

假设巡飞弹在Oxy平面以固定速度v高速突防，则控制巡飞弹航迹倾角β=0°，滚转角φ=0°，运动模型简化为

(4)

图1 巡飞弹飞行航迹示意图Fig.1 Schematic diagram of flight path of loitering munition

1.2 状态空间设计

(5)

式中：α=x(t)-xg，β=y(t)-yg；xg、yg分别为目标区域中心点的经度、纬度坐标。

1.3 动作空间设计

根据巡飞弹飞行运动模型控制量的定义，飞行动作空间定义如 (6) 式所示。

Af={Δφ},Δφ=φ(t)-φ(t-1),
-φmax<Δφ<φmax，

(6)

式中：Δφ表示两个相邻仿真时间步长间航向角的改变量。设置巡飞弹作战条令与交战规则如图2所示，主要为巡飞弹可接战临机出现目标，武器控制状态为对地自由开火，即发现目标即摧毁，开火动作不受算法控制。

图2 巡飞弹作战条令与交战规则设置Fig.2 Doctrine and engagement rules of loitering munition

1.4 奖励函数设计

巡飞弹的突防目的是机动到目标地域执行任务，设巡飞弹完成突防控制任务的条件，如(7)式所示。

(7)

式中：在巡飞弹初始发射时刻，t=0 s，t为离散值，以1 s为1个仿真时间步长；maxt为每轮训练最大仿真时间；d(t)表示t时刻，巡飞弹与目标区域中心位置AT的距离；l表示巡飞弹的探测半径。目标区域的范围是以目标点AT为圆心，以l为半径的圆形区域，如图3所示。根据巡飞弹突防控制任务完成的条件，设计巡飞弹突防控制评价函数，如(8)式所示。

图3 巡飞弹突防场景几何关系示意图Fig.3 Schematic diagram of geometric relationship of loitering munition penetration scene

(8)

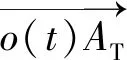
(9)

2 基于深度强化学习的巡飞弹突防控制决策模型求解

强化学习是在给定的MDP中寻找最优策略π*(a|s)=P(at=a|st=s)的过程。DRL主要是在给出状态s和qπ(s,a)，或s和vπ(s)的值后，可以借助深度神经网络(DNN)较强的拟合能力，通过模型实现s→qπ(s,a)或s→vπ(s,a)的映射关系。

2.1 基于演员- 评论家的巡飞弹突防决策框架

DRL基本可分为基于策略梯度(PG)与基于值函数两类，基于PG的DRL够直接优化策略的期望总奖励值并在策略空间搜索最优策略，适用范围更广[12-13]，因此，本节基于PG设计算法框架。

图4 巡飞弹决策网络结构Fig.4 Network structure of loitering munition penetration decision

巡飞弹在战场环境中的状态、动作、奖励值探索轨迹τ可描述为

τ={s1,a1,r1,s2,a2,r2,…,st,at,rt,st+1,
at+1,rt+1,…,sT,aT,rT}，

式中：st、at、tt分别为仿真时间，巡飞弹的状态、动作、奖励值；t=1,2,3,…,T，T为仿真终止时间。

如图5所示，τ发生的概率为

图5 巡飞弹探索轨迹示意图Fig.5 Schematic diagram of loitering munition exploration trajectory

(10)

因此，在巡飞弹的突防策略为π情况下，所能获得的期望奖励为

(11)

本节期望通过调整巡飞弹的突防策略π，使得期望奖励最大，于是对期望函数使用梯度提升方法更新巡飞弹策略网络参数θ，求解过程如下：

(12)

式中：N表示仿真的最大经验序列数；Tn表示第n经验序列的仿真终止时间。

利用该梯度调整策略参数θ，如 (13) 式：

(13)

式中：η为学习率。

(14)

因此，采用Q函数来估算R的期望值，同时，创建一个评价网络来计算Q函数值。为提升巡飞弹突防学习效率，设计巡飞弹评价网络结构如图6所示，输入层为t时刻巡飞弹状态空间、动作值，输出为Q函数值。

图6 巡飞弹评价网络结构Fig.6 Network structure of loitering munition evaluation

此时，巡飞弹策略网络的参数梯度变为

(15)

巡飞弹评价网络根据估计的Q值和实际Q值的平方误差进行更新，对评价网络来说，其损失值为

(16)

设计巡飞弹突防控制决策算法框架设计如图7所示。

图7 巡飞弹突防控制决策算法框架Fig.7 Algorithm framework of loitering munition penetration control

以上为基于演员- 评论家(AC)的DRL框架建模，属于PG方法类，但可以进行单步更新，比传统PG效率更高。

2.2 基于深度确定性策略梯度的巡飞弹突防控制决策求解

深度确定性策略梯度(DDPG)是AC框架下的算法[14]，但融合了DQN的优势，提高了AC的稳定性、收敛性，其流程示意图8[15]所示。图8中：s′、a′分别表示更新后的状态值、动作值。

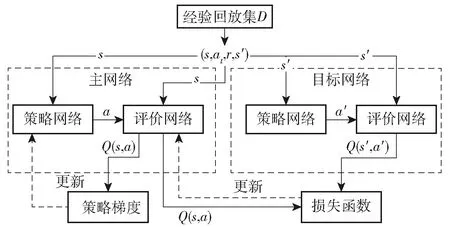
图8 DDPG算法流程图Fig.8 Flow chart of DDPG algorithm

根据上述流程，基于DDPG的巡飞弹突防控制决策算法训练流程如表1所示。

表1 巡飞弹突防控制决策算法训练流程Tab.1 Training process of loitering munition penetration control algorithm

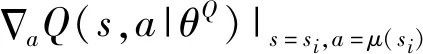
巡飞弹突防控制决策算法流程训练完毕后，得到最优决策网络μ(s|θμ)，直接使用μ(s|θμ)输出作为决策结果，即a=μ(s|θμ)，s∈S.

3 实验设计及结果分析

图9所示为巡飞弹突防敌地空导弹防御阵地，到某地域实施“斩首”行动仿真实验。

图9 巡飞弹突防想定示意图Fig.9 Schematic diagram of loitering munition penetration scenario

3.1 实验场景及武器性能参数设置

实验场景主要对巡飞弹及3个地空导弹阵地的初始位置，以及与巡飞弹突防相关的红方和蓝方主要武器性能参数进行了设置。由表2可知：地空导弹的火力射程为6.0～7.6 km，巡飞弹的飞行高度为3.658 km，当巡飞弹进入地空导弹火力范围时，即进入威胁区域；巡飞弹的侦察距离为10 km，地空导弹的火力范围为10 km，当巡飞弹距地空导弹阵地发射点10 km时，会相互探测到对方的位置坐标。导弹的爬升速度为323 m/s，爬升至巡飞弹的飞行高度需要约11.3 s时间，此时，巡飞弹以250 km/h速度可机动约785 m. 由于导弹的巡航速度为2 185 km/h，远大于巡飞弹的机动速度，因此，在导弹爬升至巡飞弹飞行高度前，巡飞弹如果没有规避到地空导弹阵地火力范围以外，就会面临被摧毁的危险；目标区域设置为：以目标点坐标为圆心，巡飞弹侦察距离为半径圆形区域，是因为这里假定巡飞弹进入该区域，即可在一定探测时间发现目标，并自动锁定将其摧毁。

表2 实验场景及主要武器性能参数设置表Tab.2 Experimental scene and weapon performance parameter setting

3.2 仿真流程及参数设置

实验软件环境：ubuntu18.04+pytorch. 硬件环境：Intel core i7+GeForce GTX 1060Ti+64G. actor、critic神经网络结构分别采用2层、3层隐藏层的全连接神经网络，隐藏单元数分别为(256，128)、(256，128，64)，并使用relu激活函数。网络主要超参数设置：actor、critic网络学习率η=0.001，折扣因子Γ=0.99，目标网络更新系数τ=0.001，经验回放池容量D=100 000，当经验回放池数据达到scale=10 000规模时，开始采用更新策略网络，采样数据规模batchsize=1 000，探索噪声ε=0.2.

3.3 实验结果分析

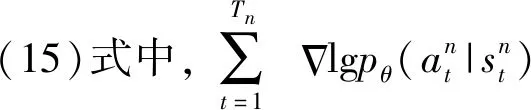
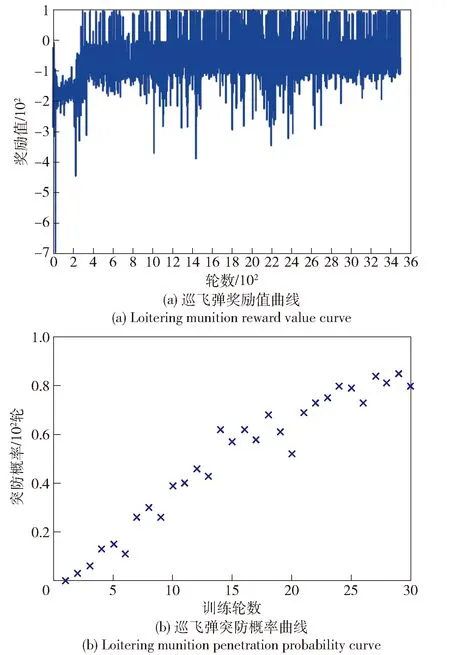
图10 训练数据统计图Fig.10 Statistical graph of training data

图11(a)为巡飞弹评价网络损失函数值曲线，由评价网络损失值函数(16)式可知：横坐标为训练周期；纵坐标为目标评价网络与主评价网络对巡飞弹状态- 动作值的估计在每个训练周期内的累积偏差，即损失值。本文以1 s为仿真时间步长，巡飞弹在每个时间步长内与环境交互采集一次数据，当经验回放池数据量达到规模scale=10 000之后，每batchsize=1 000条经验数据根据(16)式计算一次损失函数值，从图11(a)中可以看出，评价网络的损失值随训练进行不断减小，并趋近于0，这说明评价网络对巡飞弹状态- 动作的估计值趋于准确。图11(b)为巡飞弹策略网络训练目标变化图，横坐标为训练周期，纵坐标为策略网络在每次训练时目标，巡飞弹根据(21)式更新训练目标网络。从图11(b)中可以看出，策略网络训练目标随训练进行，逐渐维持在一个较小的值，说明巡飞弹突防控制策略在逐步优化并趋于稳定。

图11 巡飞弹突防控制决策模型最优策略求解过程Fig.11 Process of solving the optimal policy of loitering munition penetration control decision model

统计巡飞弹每训练M轮的平均奖励值，即

(21)

表3 巡飞弹突防平均奖励值统计Tab.3 Average reward values of loitering munition penetration

训练完成后，取Ne=3 500的巡飞弹策略模型π3 500进行1 000次突防仿真测试，数据统计结果如图12所示。

图12 巡飞弹突防仿真测试数据统计Fig.12 Data statistics of penetration simulation test for loitering munition

巡飞弹决策控制模型测试统计结果如表4所示，1 000次突防仿真测试实验，共成功突防821次，成功率为82.1%，平均决策时间1.48 ms，满足巡飞弹控制决策指标要求。

表4 决策控制模型测试统计结果Tab.4 Statistical results of decision control model test

从1 000次突防仿真测试实验中，选择3组具有代表性的巡飞弹突防轨迹样例，如图13所示。巡飞弹的初始位置在图13中绿色圆形区域内随机初始化，进而反应训练结果在该发射区域的泛化性能。目标区域为图13中橙色圆形区域，巡飞弹进入该区域成功摧毁目标，即为成功完成突防任务。图13中蓝色区域为地空导弹威胁区域，巡飞弹实施突防任务时需要即时调整突防路线，避开威胁区域。从图13中可以看出有红、绿、蓝3条不同颜色的巡飞弹突防轨迹，分别记为1号、2号、3号突防路线。

图13 巡飞弹突防仿真测试轨迹样例Fig.13 Sample trajectories of loitering munition in penetration simulation test

图14 巡飞弹突防仿真测试奖励值曲线Fig.14 Reward curves of loitering munition in penetration simulation test

图15为巡飞弹动作控制参数变化曲线，结合图13可知：在1号突防路线中，巡飞弹在突破威胁区之前，Δφ>0 rad，并且Δφ逐渐增大，后逐渐减小，实现向东平稳转向；巡飞弹临近威胁区域，Δφ减小至0 rad，并且随着距离的进一步临近，Δφ继续减小，实现向西平稳转向，从而在威胁区西侧边缘绕过；巡飞弹突破威胁区域，Δφ逐渐增大至大于0 rad，实现向东平稳转向之后，始终控制航向与任务方向保持一致，机动至目标区，实现突防。

图15 巡飞弹动作控制参数变化曲线Fig.15 Sample diagram of penetration trajectories

在2号突防路线中，巡飞弹在突破威胁区前，Δφ>0 rad，进而向东机动至临近威胁区域，随后控制航向与任务方向保持一致；Δφ在没有大的变动情况下，始终朝目标区域方向机动，从防御体系漏洞突破威胁区，实现突防。

在3号突防路线中，Δφ的变动范围较大，特别是在即将进入威胁区时，Δφ>0 rad持续增大，后持续减小至Δφ<0 rad，从而在威胁区东侧边缘绕过；在突破威胁区后，又调整Δφ，向目标区域机动，实现突防。

综上所述，3组具有代表性的突防仿真样例中，巡飞弹均能从发射区域的任意位置机动至目标区域，并将目标摧毁，决策网络具有较好的泛化能力，奖励值均层指数级增长。由此可以看出，本文所提模型可有效实现巡飞弹突防控制决策，在一定程度上提高了巡飞弹的自主性。

4 结论

本文针对巡飞弹动态突防控制决策问题，采用MDP描述了巡飞弹飞行运动模型，设计了飞行状态空间、动作空间、奖励函数等，提出基于DRL的LMPCD模型及其求解方法。仿真实验结果表明，巡飞弹在动态对抗环境中，能够实现自主突防，证明了模型及求解方法的有效性。该方法可为预测“蓝军”巡飞弹突防路线提供了技术借鉴，以及该方法以实际武器装备可获取的数据为输入，对下一步在真实环境中应用具有重要军事意义。

参考文献(References)

[1] 庞艳珂,韩磊,张民权,等.攻击型巡飞弹技术现状及发展趋势[J].兵工学报,2010,31(增刊2):149-152.

PANG Y K,HAN L,ZHANG M Q,et al.Status and development trends of loitering attack missiles [J].Acta Armamentarii,2010,31(S2):149-152.(in Chinese)

[2] 郭美芳,范宁军,袁志华.巡飞弹战场运用策略[J].兵工学报,2006,27(5):944-947.

GUO M F,FAN N J,YUAN Z H.Battlefield operational strategy of loitering munition [J].Acta Armamentarii,2006,27(5):944-947.(in Chinese)

[3] 刘杨,王华,王昊宇.巡飞弹发展背后的作战理论与概念支撑[J].飞航导弹,2018 (10):51-55.

LIU Y,WANG H,WANG H Y.Operational theory and conceptual support behind the development of loitering munition [J].Aero-dynamic Missile Journal,2018 (10):51-55.(in Chinese)

[4] 郝峰,张栋,唐硕,等.基于改进RRT算法的巡飞弹快速航迹规划方法[J].飞行力学,2019,37(3):58-63.

HAO F,ZHANG D,TANG S,et al.A rapid route planning me-thod of loitering munitions based on improved RRT algorithm [J].Flight Mechanics,2019,37(3):58-63.(in Chinese)

[5] 欧继洲,黄波.巡飞弹在陆上无人作战体系中的应用初探[J].飞航导弹,2019(5):20-24.

OU J Z ,HUANG B.Application of loitering munition in land unmanned combat system [J].Aerodynamic Missile Journal,2019(5):20-24.(in Chinese)

[6] 王琼,刘美万,任伟建,等.无人机航迹规划常用算法综述[J].吉林大学学报(信息科学版),2019,37(1):58-67.

WANG Q,LIU M W,REN W J,et al.Overview of common algorithms for UAV path planning [J].Journal of Jilin University (Information Science Edition),2019,37(1):58-67.(in Chinese)

[7] 张堃,李珂,时昊天,等.基于深度强化学习的UAV航路自主引导机动控制决策算法[J].系统工程与电子技术,2020,42(7):1567-1574.

ZHANG K,LI K,SHI H T,et al.Autonomous guidance maneuver control and decision-making algorithm based on deep reinforcement learning UAV route [J].Journal of Systems Engineering and Electronics,2020,42(7):1567-1574.(in Chinese)

[8] Bouhamed O,Ghazzai H,Besbes H,et al.Autonomous UAV navigation:a DDPG-based deep reinforcement learning approach[EB/OL].[2020-07-11].http:∥arxiv.org/pdf/1509.02971.pdf.

[9] 张建生.国外巡飞弹发展概述[J].飞航导弹,2015(6):19-26.

ZHANG J S.Overview of foreign cruise missile development [J].Aerodynamic Missile Journal,2015 (6):19-26.(in Chinese)

[10] 李增彦,李小民,刘秋生.风场环境下的巡飞弹航迹跟踪运动补偿算法[J].兵工学报,2016,37(12):2377-2384.

LI Z Y,LI X M,LIU Q S.Trajectory tracking algorithm for motion compensation of loitering munition under wind environment [J].Acta Armamentarii,2016,37(12):2377-2384.(in Chinese)

[11] 黎珍惜,黎家勋.基于经纬度快速计算两点间距离及测量误差[J].测绘与空间地理信息,2013,36(11):235-237.

LI Z X,LI J X.Quickly calculate the distance between two points and measurement error based on latitude and longitude[J].Geomatics &Spatial Information Technology,2013,36(11):235-237.

[12] 刘建伟,高峰,罗雄麟.基于值函数和策略梯度的深度强化学习综述[J].计算机学报,2019,42(6):1406-1438.

LIU J W,GAO F,LUO X L.A review of deep reinforcement learning based on value function and strategy gradient [J].Chinese Journal of Computers,2019,42(6):1406-1438.(in Chinese)

[13] 刘全,翟建伟,章宗长.深度强化学习综述[J].计算机学报,2018,41(1):1-27.

LIU Q,ZHAI J W,ZHANG Z C.A survey on deep reinforcement learning [J].Chinese Journal of Computers,2018,41(1):1-27.(in Chinese)

[14] KONDA V R,TSITSIKLIS J N.Actor-Critic algorithms[C]∥Proceedings of Advances in Neural Information Processing Systems.Denver,CO,US:NIPS Foundation,2000:1008-1014.

[15] LILLICRAP T P,HUNT J J,PRITZEL A,et al.Continuous control with deep reinforcement learning[EB/OL].[2020-07-11].http:∥arxiv.org/pdf/1509.02971.pdf.