基于非参数核密度估计法的车辆大数据服役载荷外推方法
2021-06-23于佳伟郑松林赵礼辉
于佳伟 郑松林 赵礼辉 井 清
1. 上海机动车检测认证技术研究中心有限公司,上海,201805 2. 上海理工大学机械工程学院,上海,200093 3. 上汽集团商用车技术中心,上海,200438
0 引言
对汽车产品而言,高耐久性里程与高可靠性指标要求是保证车辆产品品质的基本前提[1]。在车辆产品耐久性与可靠性评价中,试验规范尤为重要。一套合理的试验规范既可有效保证产品的用户使用可靠度,又有益于产品的轻量化设计。
在车辆产品耐久性试验规范制定方法方面,已有文献对此展开了相关研究,例如,结合定远试验场实车载荷谱采集和有限元分析方法制定钢板弹簧的加速寿命试验程序载荷谱[2];基于襄樊试车场实测载荷谱制定车身[3]和后桥[4]疲劳试验的程序载荷谱;以及由汽车控制臂实测载荷谱转化为台架疲劳试验谱[5-6]等。现有文献中关于道路载荷谱向台架试验载荷谱的当量等效转化方法的研究较多,为耐久性试验规范的制定提供了参考。
对车辆服役载荷特征的充分研究是制定耐久性试验规范的关键。若试验规范制定的数据依据仅是汽车试验场载荷谱,可能导致产品在试验验证阶段无法完全暴露潜在的用户使用过程中的失效模式。为了使试验规范能够完全反映用户实际使用情况,有必要对车辆用户道路的服役载荷特征展开研究。张禄[7]基于参数法概率密度估计,研究了某大型营运客车在用户道路载荷条件下轴头和质心三向加速度幅值、前悬稳定杆扭转和平衡梁弯曲应变幅值的概率密度分布。赵礼辉等[8]基于参数法概率密度估计,建立了用户使用条件下轻型商用车年行驶里程、行驶车速和载重等的概率密度分布模型。
在用户实际使用过程中,车辆承受的载荷环境复杂多变,通常难以用固定形式的概率密度分布函数对载荷的分布进行拟合,导致参数法概率密度估计应用的局限性。非参数法概率密度估计不需要假设变量的分布函数形式,概率密度估计结果完全由样本数据自身的分布决定,能够灵活准确地得到变量的概率密度估计结果,可有效解决分布形式复杂的随机变量的概率密度估计问题[9]。
非参数法概率密度估计在诸多领域的机械承载结构载荷特征研究中得到了应用。例如,在轨道交通方面,金新灿等[10]以高速动车组动车轮轴动应力线路实测数据为依据,采用非参数核密度估计法对实测高速轮轴载荷谱进行了拟合外推分析;李凡松等[11]利用非参数二维核密度估计法,提出了多载荷时间历程输入条件下的车下设备承载结构疲劳试验载荷谱编制方法。在工程机械方面,高天宇等[12]基于非参数核密度估计法建立了装载机转斗液压缸铲掘阶段八级程序载荷谱。此外,在农业机械方面,宋清椿等[13]以田间作业动力机械车架为研究对象,采用非参数核密度估计法对车架载荷进行非参数雨流外推,并基于外推结果进行了疲劳寿命预测。
道路车辆承载结构载荷谱因路面特征和驾驶员操作行为不同等因素影响而呈现出较强的随机性,载荷分布特征差异较大,通常不服从特定的分布函数形式,因此有必要采用非参数概率密度估计方法研究道路车辆承载结构随机载荷谱的统计分布特征。考虑到车辆服役载荷特征的研究对车辆产品耐久性和可靠性试验规范制定工作的重要性,本文以某型宽体轻客服役载荷特征的全国大范围用户使用习惯数据调研和道路载荷谱采集为数据研究基础,运用非参数核密度估计统计学方法结合蒙特卡罗仿真方法,研究用户使用习惯特征的统计方法和车辆服役载荷的外推方法,提出了一套基于用户使用习惯关联的车辆服役载荷的外推方法与流程,构建了该车型减振弹簧应变的全寿命周期服役载荷谱。
1 用户使用习惯特征统计与分析
1.1 非参数一维核密度概率密度估计方法
概率密度估计方法分为参数法和非参数法。由于非参数法不需设定分布函数的具体形式,概率密度估计结果完全由样本数据自身的分布决定,相比参数法能给出较为准确的密度估计结果。考虑到不同用户使用习惯之间的差异较大,致使用户使用习惯特征的分布不遵循固定的形式,因此本文采用非参数核密度估计法统计用户使用习惯特征。
一维核密度估计法的原理如下:设xi(i=1,2,…,n)是从一维总体X中抽出的独立同分布的样本数据,X具有未知的密度函数f(x),如果存在(-1,1]上的均匀密度函数K(u)≥0且满足
则f(x)的核密度估计为
式中,K(·)为核函数;h为带宽;n为样本容量。
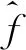
式中,f为真实密度函数,f″表示函数f的二阶导数。
我们的内分泌功能受到复杂调控系统的控制,同时也受人体发育不同时期和生活环境的影响,如果这些影响过大,就会导致内分泌功能紊乱。《黄帝内经》提倡“饮食有节,起居有常,不妄作劳”,要求我们遵循自然规律,合理饮食,按时作息,这是一切养生方法的基础;同时要有乐观的生活态度,保持心情舒畅,这样才能使肝气条达顺畅。
通过求取最小化AMISE,得到最佳带宽
此时最小化AMISE为
其中,[σKR(K)]4/5项与核函数K有关,因此选择的最佳核函数K应使[σKR(K)]4/5的值最小。当核函数为以下二次项形式时可使得[σKR(K)]4/5最小:
此即为Epanechnikov核函数。几种常用核函数如表1所示,相比于矩形核,Epanechnikov核和高斯核能够获得更为光滑的概率密度估计结果。

表1 几种常用核函数
1.2 用户使用习惯典型特征统计与分析
采用非参数一维核密度估计法研究用户使用习惯特征。首先以年行驶里程为例,研究用户年行驶里程调研结果的统计分布特征。年行驶里程通过查询用户车辆仪表盘里程(km)除以当前车龄(年)计算得到。统计结果的直方图概率密度估计如图1所示。基于参数法概率密度估计结合极大似然估计方法,得到几种常用连续型分布函数的概率密度拟合结果如图1所示,对数正态分布对样本数据的拟合效果最好,但仍然与实际样本数据的分布存在一定的误差,因此,基于非参数一维核密度估计法,应用高斯核和Epanechnikov核分别对实测样本数据进行密度估计,两种核函数密度估计结果基本相同,并与实际样本数据的分布十分吻合,明显优于对数正态分布,如图2所示。
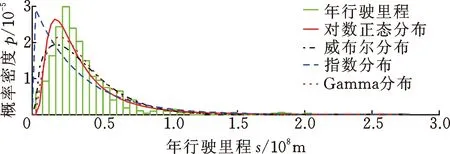
图1 几种常用连续型分布的概率密度估计
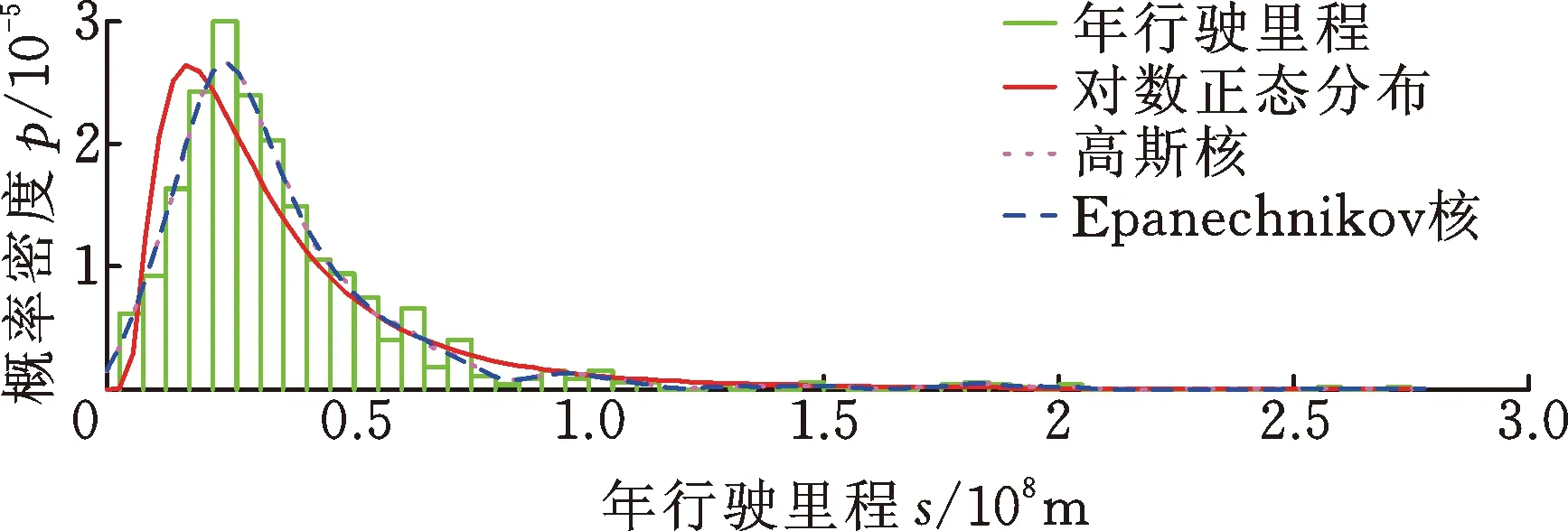
图2 非参数一维核密度估计
对于本文重点关注的90%分位用户年行驶里程,采用高斯核和Epanechnikov核密度估计法得到90%分位用户年行驶里程分别为61 900 km和61 978 km。鉴于两种核密度估计结果与实测样本数据分布较为一致,因此取高斯核和Epanechnikov核密度估计结果的均值作为最终结果,则90%分位用户年行驶里程估计值为61 939 km。
除年行驶里程外,本文还分别计算了90%分位用户期望车辆服役里程和不同道路类型的用户行驶里程比例。分析用户期望车辆服役里程有助于设定合理的车辆耐久性目标,通过采用相同的统计分析方法与流程,得到90%分位用户期望服役里程估计值为593 000 km。由于在不同道路条件下车辆所承受的载荷差异较大,为合理构建车辆服役载荷谱,有必要对用户在不同道路类型下的行驶里程比例进行估计,通过采用相同的统计分析方法与流程,得到90%分位用户城市道路行驶里程比例、高速公路行驶里程比例、郊区道路行驶里程比例和恶劣道路行驶里程比例估计值分别为40%、33%、23%和4%。经以上统计分析得到的用户使用习惯特征的90%分位估计值归纳在表2中。
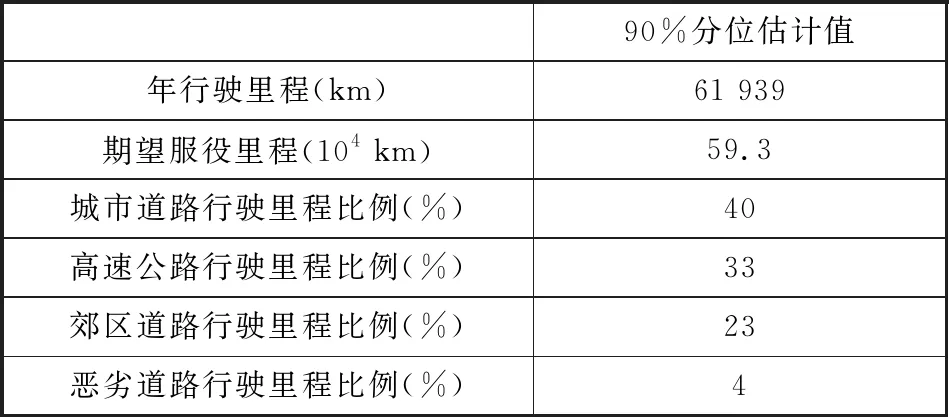
表2 用户使用习惯特征的90%分位估计值
2 用户道路大数据载荷谱采集
用户道路载荷谱采集是掌握用户道路载荷特征的最直接和有效的方法,同时也为车辆全寿命周期服役载荷谱的建立提供了载荷谱样本。在全国范围内对该车型开展了载荷谱采集,采集路线涉及全国21个省,总里程约为18 000 km,其中各道路类型的载荷谱采集里程如表3所示。该客车前悬架为麦弗逊式独立悬挂,为采集减振器弹簧的道路载荷谱,沿弹簧轴向布置了T型全桥应变片,如图3所示,测量弹簧的扭转载荷谱。图4展示了一段城市道路载荷谱,所采集到的载荷谱为载荷-时间历程形式,里程约52 km,以左前减振器弹簧应变通道为例。在应用于载荷特征计算之前,对采集到的载荷谱进行了剔除尖峰异常值和纠正漂移等信号预处理工作,保证用于计算分析的载荷谱能够代表用户道路的真实载荷环境。
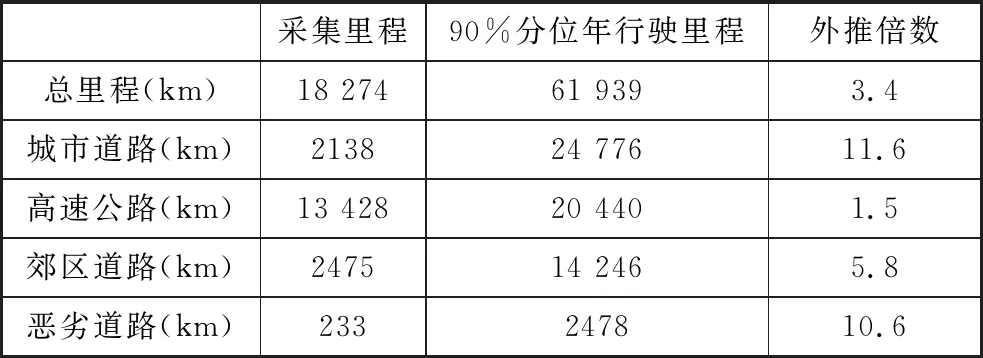
表3 各道路类型载荷谱采集里程和外推倍数

图3 前减振器弹簧应变片
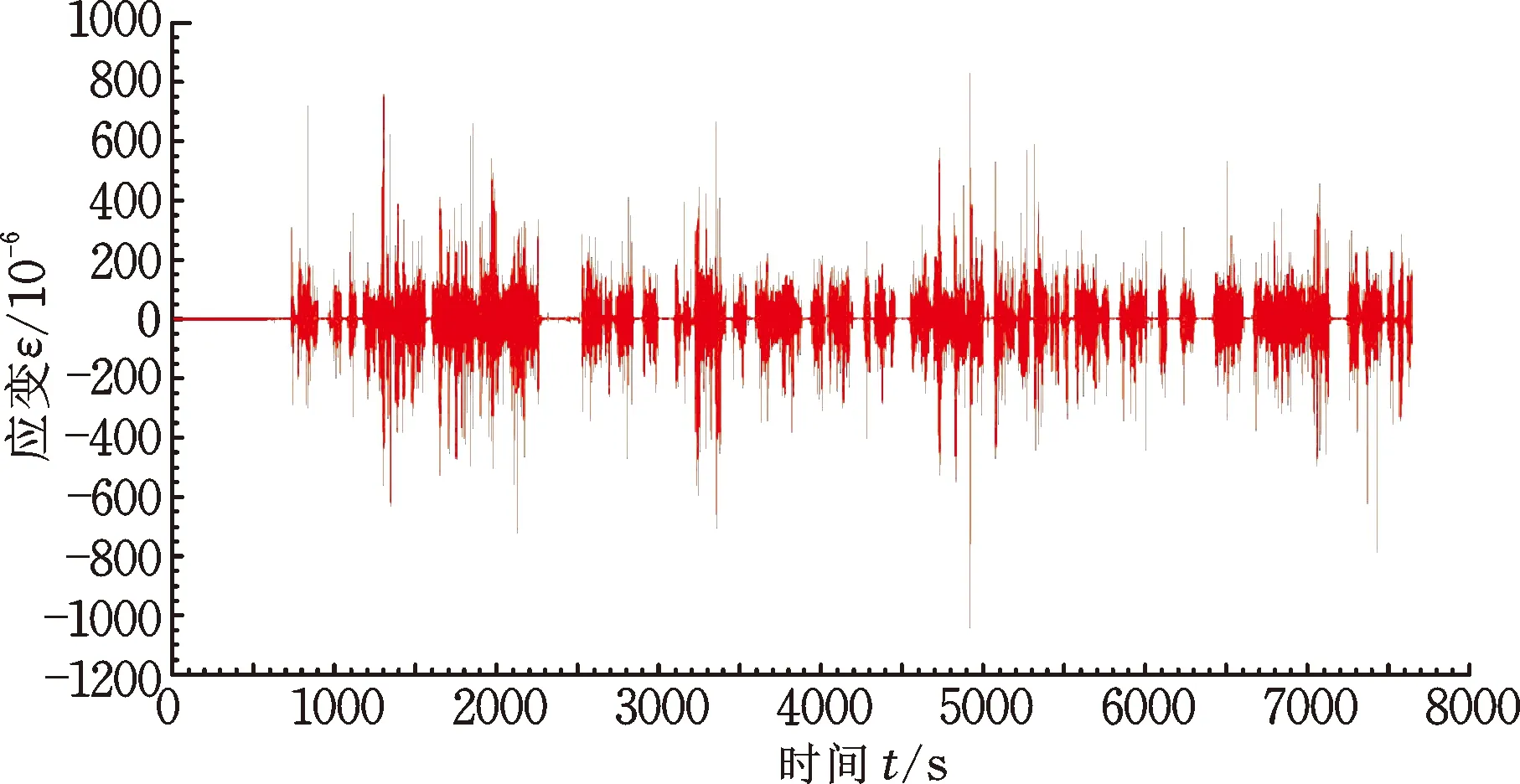
图4 杭州城市道路载荷谱
3 载荷谱外推方法与流程
建立车辆全寿命周期服役载荷谱是为了合理地制定零部件的疲劳耐久评价试验规范。对疲劳寿命分析而言,载荷的幅值域特征被认为是影响疲劳寿命的主要因素。雨流循环计数法属于双参数循环计数法,记录了载荷循环的二维信息,如起始值和终点值或幅值和均值,与材料的应力-应变迟滞回线相对应,具有较为明确的力学概念。雨流循环计数法通过对载荷-时间历程进行循环计数,可获得载荷均幅值与其作用次数间的对应关系,因而被认为是目前预测疲劳寿命较好的方法。此外,由于雨流循环矩阵包含详细的载荷循环的均幅值信息,有利于转换为疲劳耐久试验规范,因此本文采用非参数二维核密度估计法对用户道路实测载荷谱的雨流矩阵展开外推,建立该车型的全寿命周期服役载荷谱。
3.1 非参数二维核密度估计法
一维核密度估计法适用于一维随机变量的概率密度估计问题,而对于二维乃至多维随机变量的概率密度估计问题,则需要采用多维核密度估计法。多维核密度估计法和一维核密度估计法的基本原理相同。多维核密度估计法的通用表达形式为
式中,X为多维数据总体;Xi为观测到的第i个多维数据样本;H为非奇异d×d带宽矩阵;Kd为d维概率密度函数。
对于二维核密度估计,常用的两种核函数类型为二维正态密度函数和二维Epanechnikov核函数。二维正态密度函数表达式为
式中,x和y分别代表了二维数据的两个维度。
二维Epanechnikov核函数表达式为
若带宽矩阵H按H=hA的形式取值,且A取为单位矩阵,则二维核密度估计法可表示为
(10)
式中,xi和yi表示从二维数据总体中抽取的两个维度的样本数据。
3.2 用户道路载荷外推流程
载荷外推需明确两个关键内容,即载荷数据对象和外推目标里程。载荷数据对象选为用户道路实测载荷谱,考虑到不同道路类型的载荷环境差异较大,本文按照不同道路类型分别展开外推。为避免外推倍数过大,同时考虑以年为周期对车辆服役载荷进行划分较为合理,因此选择年行驶里程作为外推目标里程。本文提出的用户道路载荷外推流程如图5所示,共有两处采用非参数核密度估计法,其中用户使用习惯典型特征的数据为一维随机变量,采用一维核密度估计法研究其分布特征;而用户道路载荷谱雨流矩阵的数据形式为二维随机变量(载荷起始点和终止点),因此采用二维核密度估计法对其进行概率密度估计。载荷外推倍数由各道路类型的年行驶里程统计值除以实测载荷谱里程得到,如表3所示。将外推后各道路类型的载荷叠加,得到年行驶里程用户载荷。最后,按照用户期望服役里程与年行驶里程间的倍数,以年行驶里程用户载荷为基本单位进行载荷叠加,构建车辆全寿命周期服役载荷谱。
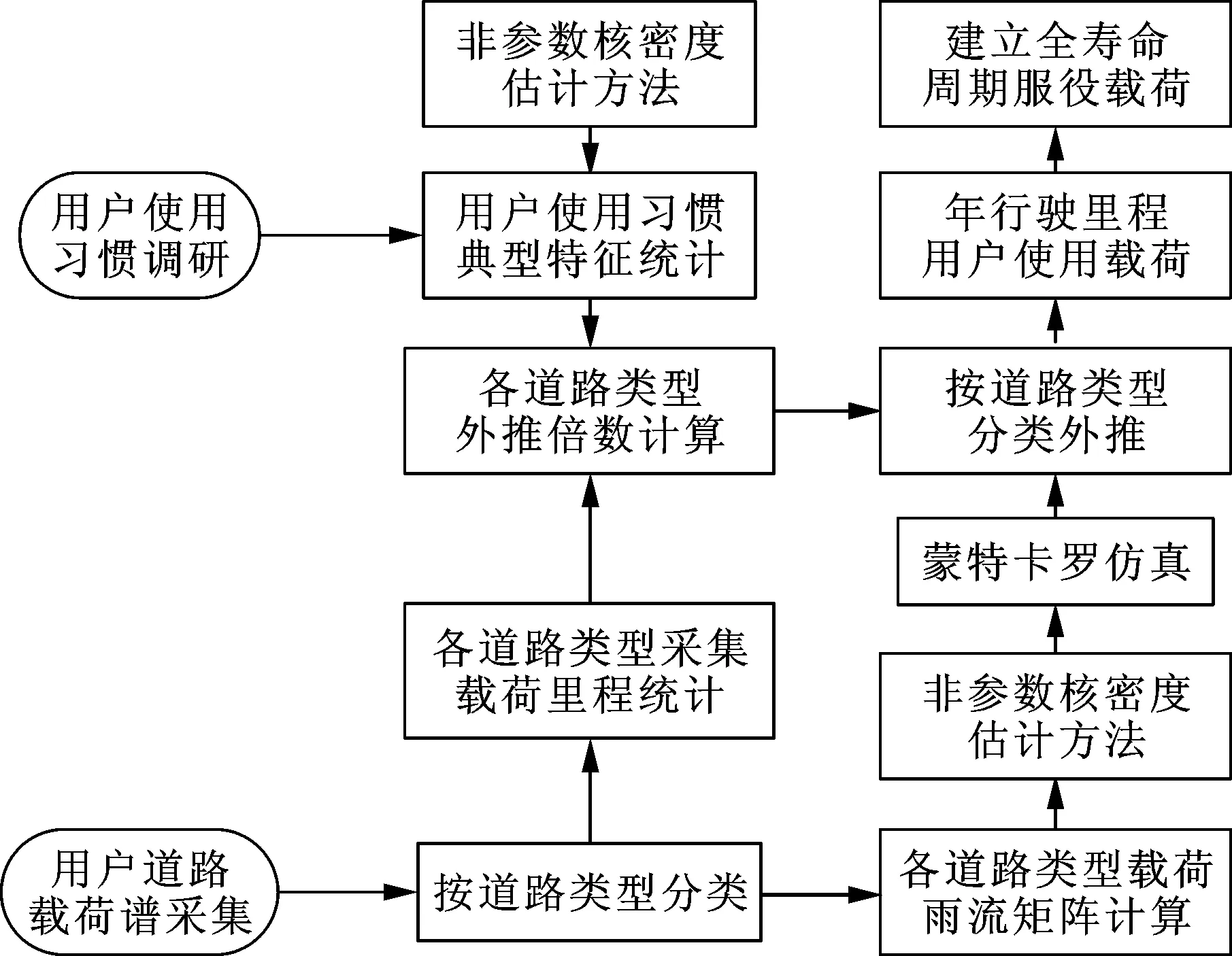
图5 用户道路载荷外推流程
4 车辆全寿命周期服役载荷谱构建
依据图5的流程,本文将以道路类型分类进行载荷外推,由于篇幅所限,以郊区道路载荷谱为例,详细阐述载荷外推的过程。
4.1 载荷谱雨流矩阵计算
首先对采集的载荷谱按道路类型分类,统计每段载荷谱的载荷最大值和最小值,确定合理的雨流矩阵坐标界限。之后逐一计算每段载荷谱的雨流矩阵。为便于对雨流矩阵进行概率密度估计,雨流矩阵采用from-to的形式表示,且删除了载荷变程为最大变程5%以下的低幅值载荷,这些低幅值载荷的循环数目所占比例大,且对结构件造成的损伤几乎可以忽略。将郊区道路所属载荷谱的雨流矩阵进行叠加,得到郊区道路实测总载荷的雨流矩阵如图6所示,图中横坐标表示载荷的起始点,纵坐标表示载荷的终止点,而最右侧的标识图表示雨流矩阵中各单元载荷的重复次数。从图6中可知,矩阵副对角线上的小变程载荷已被删除,矩阵主对角线上显示存在个别大变程载荷。

图6 郊区道路实测总载荷的雨流矩阵
4.2 雨流矩阵概率密度估计和里程外推
运用非参数二维核密度估计法,分别采用Epanechnikov核和高斯核对郊区道路总载荷雨流矩阵进行概率密度估计,结果如图7所示。两种核密度估计结果在分布形态上大体一致,但高斯核在大变程载荷区域(矩阵主对角线两端)内的概率密度估计范围比Epanechnikov核略广,分布形态更饱满。基于这两种核密度估计结果,结合蒙特卡罗仿真方法,按表3中郊区道路里程外推5.8倍,两种核密度估计法第一次载荷里程外推结果如图8所示。两种方法外推后载荷的分布形态较为一致,均极大地丰富了原实测载荷的分布区域。
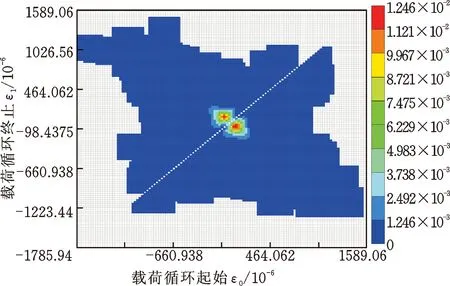
(a) Epanechnikov核
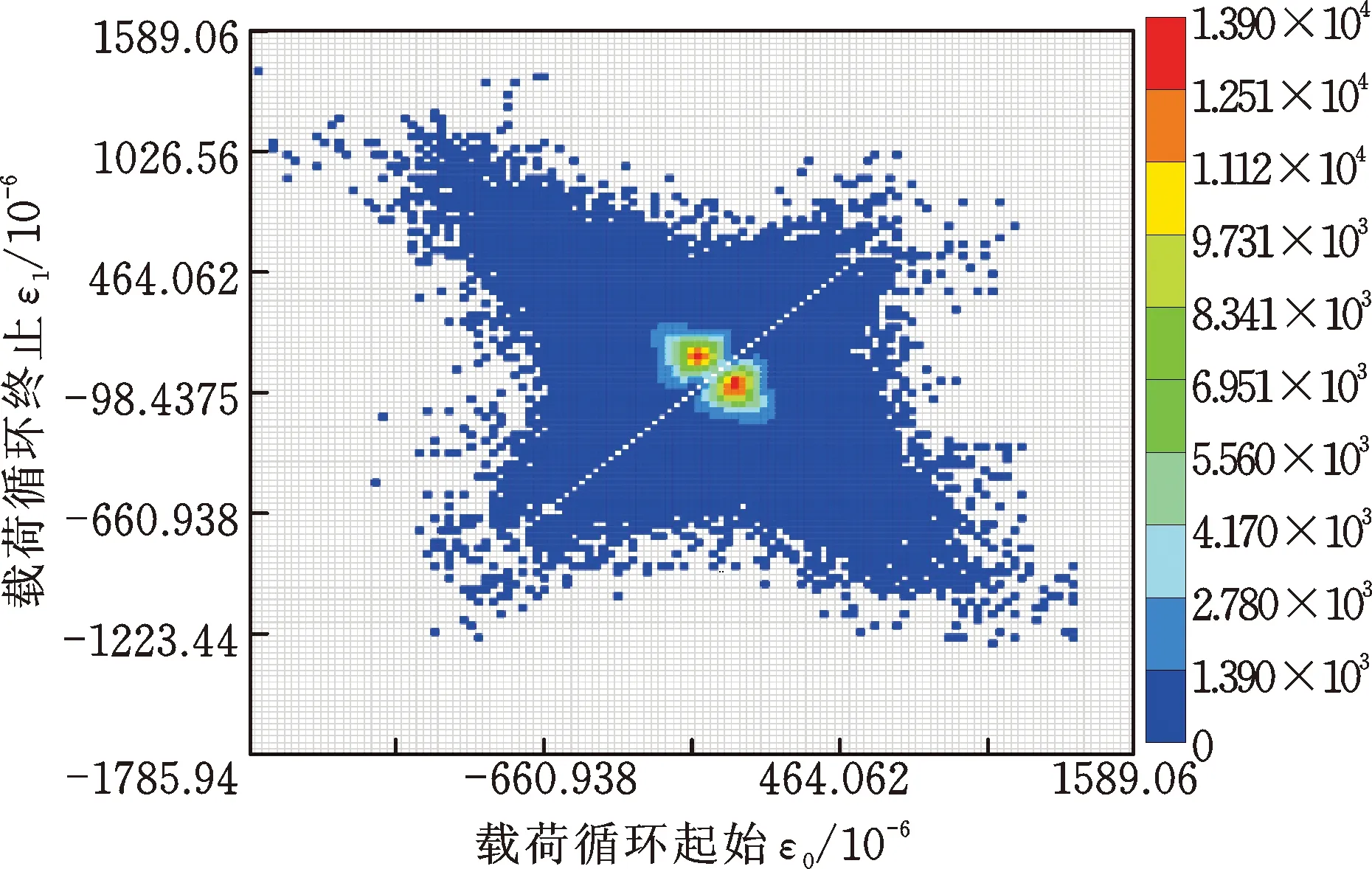
(a) Epanechnikov核
4.3 多次外推过程的一致性分析
基于载荷雨流矩阵的概率密度估计结果,结合蒙特卡罗仿真方法进行载荷里程外推。在载荷里程外推过程中,每个载荷循环按所估计的雨流矩阵分布概率随机地分配到雨流矩阵中的不同位置,因此外推的结果不是唯一的。为了研究外推结果的可能性,本文基于Epanechnikov核和高斯核的概率密度估计结果分别进行了20次载荷外推仿真。两种核密度估计法多次外推仿真结果的累计循环计数如图9所示,可见多次外推结果的载荷变程的分布基本一致,并且较好地保留了原载荷变程的分布趋势。
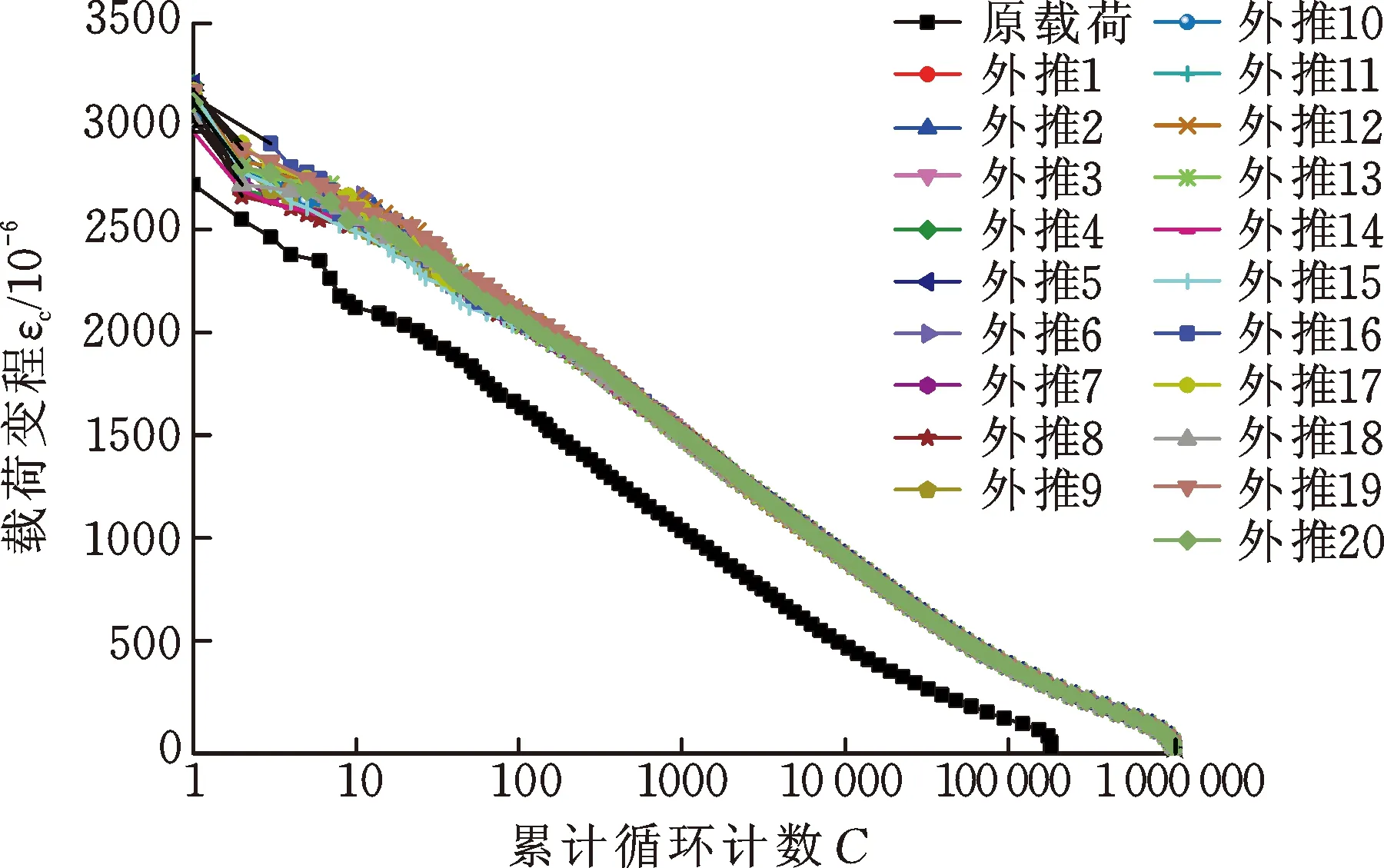
(a) Epanechnikov核
此外,计算了外推后载荷的最大变程和总伪损伤相对原载荷的增大倍数,载荷伪损伤的计算参照文献[14]中所述的方法,两种核密度估计法多次外推仿真结果的载荷最大变程和总伪损伤变化倍数如图10所示。对于载荷最大变程,两种方法多次外推结果的一致性较好,均保持在原载荷最大变程的1.1~1.2倍之间;对于载荷总伪损伤,基于高斯核的多次外推结果保持在原载荷的6.2倍左右,而基于Epanechnikov核的多次外推结果保持在原载荷的6.0倍左右。基于高斯核外推后载荷的总伪损伤略大于基于Epanechnikov核外推后载荷的总伪损伤,这是由于高斯核在大变程载荷区域(矩阵主对角线两端)内的概率密度估计范围比Epanechnikov核略广,分布形态的估计也更为饱满。但两种方法各自多次外推后载荷总伪损伤的一致性较好。以上分析结果表明两种核密度估计法的多次外推后载荷的幅值、分布和损伤的一致性均较好。对于这两种核密度估计法,各自多次外推后载荷间的差异很小。
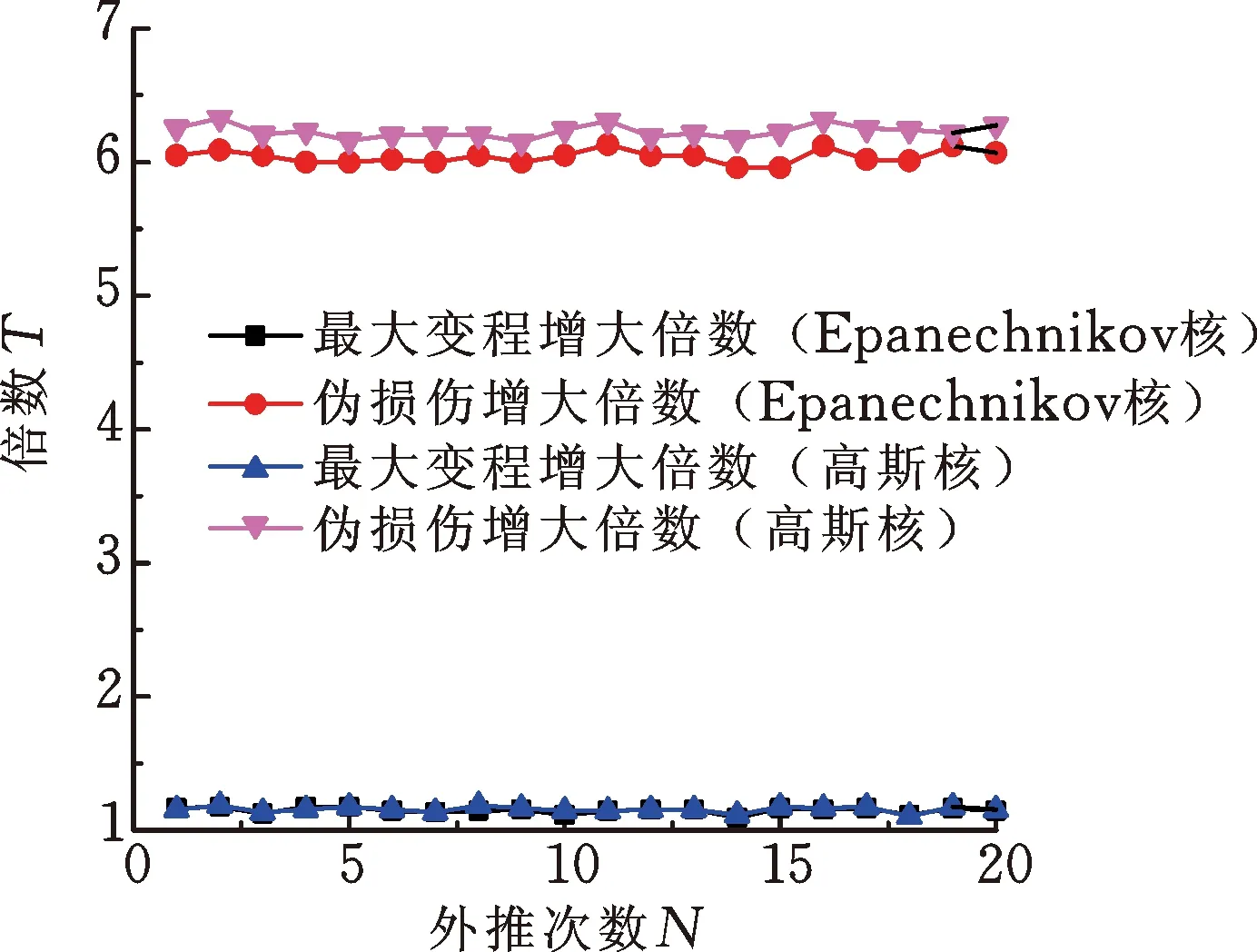
图10 多次载荷外推结果的载荷最大变程和总伪损伤变化
4.4 车辆全寿命周期服役载荷的建立
考虑到两种核密度估计法多次载荷外推结果的一致性较好,且基于高斯核外推后载荷的总伪损伤略大于基于Epanechnikov核外推后载荷的总伪损伤,从车辆产品耐久性验证的保守性考虑,选择基于高斯核外推后载荷总伪损伤最大的一次外推结果(具体为第2次外推,伪损伤为原载荷的6.33倍)作为郊区道路年行驶里程载荷。其他道路类型年行驶里程载荷的建立采取与郊区道路相同的方法进行,最后将各道路类型外推后年行驶里程载荷的雨流矩阵进行叠加,得到外推后年行驶里程总载荷的雨流矩阵如图11所示,原实测载荷谱的总雨流矩阵如图12所示,可见,外推后总载荷在保持原实测载荷分布趋势的条件下,极大地丰富了原实测载荷,使得总载荷的变化范围更广,载荷分布形态也更加饱满,并且未引入极端载荷。图11和图12中色标的最大值(9.112×104和2.996×104)表示雨流矩阵中某一单元载荷的最大重复次数。外推倍数为3.4倍,外推的过程实质上是将雨流矩阵中的载荷单元依据概率密度分布和外推倍数随机分配的过程,因此外推后雨流矩阵中所有载荷单元的重复次数之和为外推前的3.4倍,但每个载荷单元的最大重复次数不一定为3.4倍,如图11和图12雨流矩阵中载荷重复次数最大的单元,外推后其次数扩大了近3倍。外推后年行驶里程总载荷的伪损伤为原实测载荷伪损伤的5.41倍,而里程外推的倍数为3.4倍,从损伤倍数的变化也说明了外推后的总载荷极大地丰富了原实测载荷的变化范围。依据表2中用户期望服役里程与年行驶里程之间的倍数关系,以车辆年行驶里程载荷作为一个耐久循环周期,将图11中所构建的年行驶里程载荷雨流矩阵按照倍数关系线性叠加,即可得到该车型前减振器弹簧应变的全寿命周期载荷。全寿命周期载荷的建立可为后续结构件疲劳寿命的仿真计算和台架试验规范的制定工作提供充足的载荷数据依据。
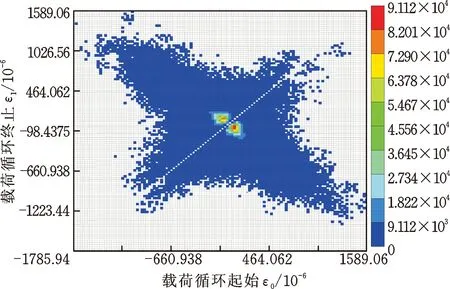
图11 外推至年行驶里程的所有道路载荷雨流矩阵
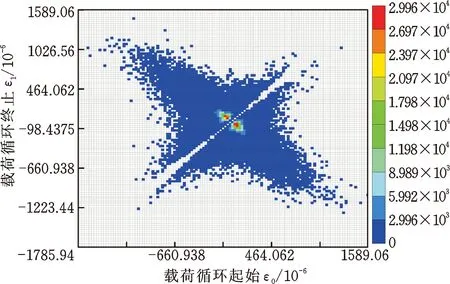
图12 所有道路实测总载荷的雨流矩阵
5 结论
(1)非参数核密度估计法较之参数法能够更准确地描述实际样本数据的分布特征,能够更真实地反映用户使用习惯典型特征的真实值。
(2)提出了车辆全寿命周期服役载荷的外推方法与流程。以年行驶里程为耐久循环周期,采用非参数二维Epanechnikov核和高斯核密度估计法,结合蒙特卡罗仿真,分别对实测载荷谱的雨流矩阵开展了载荷里程外推。
(3)基于Epanechnikov核和高斯核的概率密度估计结果分别进行了多次载荷外推仿真。多次外推结果的载荷变程的分布基本一致,并且较好地保留了原载荷变程的分布趋势。两种方法各自多次外推后载荷最大变程和总伪损伤的一致性较好。对于这两种核密度估计法,各自多次外推后载荷间的差异很小。
(4)基于高斯核外推后载荷的总伪损伤略大于基于Epanechnikov核外推后载荷的总伪损伤,这是由于高斯核在大变程载荷区域内的概率密度估计范围比Epanechnikov核略广,分布形态的估计更为饱满,致使外推后大变程载荷区域内的载荷循环数目更丰富,总伪损伤也略大。
(5)考虑到基于高斯核密度估计法外推后载荷更为保守,采用高斯核密度估计法构建了该车型前减振器弹簧应变的年行驶里程载荷雨流矩阵。外推后总载荷在保持原实测载荷分布趋势的条件下,极大地丰富了原实测载荷,使得总载荷的变化范围更广,载荷分布形态更饱满,并且未引入极端载荷。
