南京未来花园单个树状结构设计及承载性能分析*

邬红茹， 王综轶， 孙 洲， 王元清

(1 中国建筑设计研究院有限公司， 北京 100044； 2 华中科技大学土木与水利工程学院， 武汉430074；3 清华大学土木工程系， 北京100084)

0 前言

基于以上考虑，该项目顶棚采用有机玻璃(又名亚克力)材料，不锈钢结构作为支撑。方案初选中，除有机玻璃之外，顶棚可选材料还有钢化玻璃和其他塑料。但是，有机玻璃与钢化玻璃相比具有透光率高、可本体聚合、无自爆危险的优点；与其他塑料相比，耐候性更好，能保证长期使用的要求。

国外已有诸多有机玻璃建筑工程，如慕尼黑奥运体育场、格拉茨美术馆、尼日利亚的Godswill Akpabio国际体育馆等等。在我国，有机玻璃主要使用在水族馆、飞机、潜水艇、高能物理设备(如中微子探测器[1-5])等领域，在建筑中主要作为第二表皮使用，而非主要受力构件。南京未来花园将成为我国首个将有机玻璃作为主要受力构件在超大型建筑领域应用的工程案例。

1 工程概况和设计

南京未来花园总用地面积为25.54万m2，总建筑面积为9.7 865万m2，其中植物园(图1)面积为2.7万m2。植物园的主要结构形式为树状结构，如图2(a)所示，整个植物园由42个相同树状结构组成。主支撑结构均选用不锈钢材料，其截面尺寸见表1。其中柱子由5个相同箱形截面杆件焊接而成。

图1 南京未来花园建筑效果图

图2 结构形式

顶棚为有机玻璃面板，直径为21m，厚度为35mm。两相邻有机玻璃面板之间设置了伸缩缝以保证有机玻璃在温度变化时能自由伸缩。伸缩缝使用硅橡胶胶条和硅酮密封胶进行密封处理。由于每个树状结构的有机玻璃面板直径较大，难以一次成型，因此采用本体聚合的方法将数个小的有机玻璃面板聚合形成整个大的圆盘。圆盘的下表面布置有机玻璃肋(图2(b))，其高度200mm，宽度50mm。有机玻璃肋与圆盘同样采用本体聚合的方法连接。使用不锈钢支撑杆将有机玻璃与主支撑结构连接，节点位于有机玻璃肋上，每个树状结构包含66个不锈钢支撑杆。有机玻璃面板上方有100mm厚的景观水池，因此整体结构承受水压力。

不锈钢结构杆件的截面尺寸 表1

不锈钢的工程应用相对成熟，其设计可参考《不锈钢结构技术规程》(CECS 410—2015)[6]。然而，有机玻璃的结构设计却无标准可依。有机玻璃属于高分子材料，其母材抗拉强度可达65～120MPa，本体聚合拼接缝的强度可达58～100MPa[7]。但是对于有机玻璃而言，即使在常温下，受到永久荷载时也会产生蠕变，因此在设计有机玻璃工程时一般需保守考虑[8]。根据已有的工程经验[1-5]和材料蠕变试验[9]，设计有机玻璃时可通过应力控制法，即有机玻璃上最大应力小于3.5MPa。研究表明，有机玻璃板厚板(厚度大于14mm)破坏形式是脆性的[5,7]。第一强度理论适用于脆性材料受拉破坏，但是其缺点是无法考虑材料受压破坏。对于本工程有机玻璃面板和有机玻璃肋，主要考察第一主应力；对于节点区域，由于其应力状态较为复杂，主要考察von Mises应力。

图3 有机玻璃肋上节点自由度释放

结构设计中需考虑的荷载有：结构自重、水压力、风荷载、温度作用、地震作用。结构自重的荷载分项系数取1.3。有机玻璃面板上方水面高度为100mm，由于整体有机玻璃面板连通，水面高度保持不变，但是考虑到面板局部区域在荷载作用下挠度较大，从而造成附加水压；计算中将水压力作为活荷载，考虑1.5倍的荷载分项系数，而不再另外考虑附加水压的影响。另外，南京地区基本风压[10]取0.4kN/m2，风荷载体型系数取+0.7，荷载分项系数取1.5，组合系数取0.6[10]。有机玻璃的线膨胀系数较大，在温度的升高和降低过程中，面板会随之膨胀或收缩，为避免有机玻璃由于形变而造成的巨大支座反力，支撑杆与有机玻璃的连接节点设计为滑动式支撑节点，每个节点释放径向自由度，约束环向和竖向自由度，如图3所示。在初步分析计算中，只考虑结构自重、水压力和风荷载三种荷载的组合，温度作用和地震作用的影响后文单独考虑。

2 结构承载性能分析

设计中首先要考虑结构的静力承载性能，由于有机玻璃的设计是该工程的设计难点，因此本文重点关注有机玻璃的受力性能。如前所述，设计中需控制有机玻璃上的应力不超过3.5MPa，这一要求是偏保守的，在设计中不再考虑抗力分项系数。

2.1 有限元模型

采用ABAQUS软件进行建模分析，整体模型见图4(a)。不锈钢(S31603)杆件均采用B31单元，有机玻璃面板和有机玻璃肋采用S4R单元。不锈钢的密度8.0×103kg/m3，弹性模量193GPa，泊松比0.3，线膨胀系数1.6×10-5/℃[6]。不锈钢采用理想弹塑性本构模型，屈服强度170MPa。有机玻璃的密度1.19×103kg/m3，弹性模量3.2GPa，泊松比0.36，线膨胀系数7.0×10-5/℃。有机玻璃是一种粘弹性材料，但是在设计使用中其应力控制在非常低的范围，因此有机玻璃的本构模型可假设为线性的。为了模拟滑动式支撑节点，将支撑杆的上端点与有机玻璃肋上对应节点的环向和竖向自由度进行耦合(图4(b))，其他自由度不约束。

核桃是本地传统栽植的果树之一，在十堰市已有千年栽培历史。近年来，十堰市将核桃产业作为农民增收的重要途径，积极引导农民大力发展核桃产业，本地的核桃种植面积逐年增加，基地建设也初具规模。在核桃产业发展过程中，必须要积极加强对核桃栽培技术要点的把握，从建园、定植、施肥、修剪、病虫害防治等方面着手，提高核桃生长水平。

图4 有限元模型

在分析静力承载性能时考虑了三种工况组合：1.3×结构自重(工况1)、1.3×结构自重+1.5×水压力(工况2)、1.3×结构自重+1.5×水压力+0.6×1.5×风荷载(工况3)。水压力和风荷载均施加在有机玻璃面板上表面，同时约束不锈钢柱底部节点所有自由度。

值得一提的是，计算结构应力水平(承载能力极限状态)时考虑了荷载分项系数，但计算结构变形(正常使用极限状态)时没有考虑荷载分项系数。

2.2 计算结果

有限元计算结果见表2和图5。有机玻璃最大应力均位于肋上，因此本文主要关注有机玻璃肋上的应力分布。由表2及图5可知，在三种工况下，有机玻璃肋上的第一主应力均不超过3.5MPa，满足强度设计要求。工况3下有机下玻璃肋的最大von Mises应力为3.79MPa，大于3.5MPa，位于支撑杆与肋的连接节点处(图6(a))。在有限元模型中对该节点进行了简化，使用两点耦合处理，因此该处变成了点与点的接触。在实际工程中，该点采用滑动支座，会局部加大有机玻璃肋的受力面积(图6(b))，因此应力会有所降低，真实von Mises应力需根据实际节点模型计算确定。

静力分析计算结果(最大值) 表2

图5(c)为有机玻璃面板在工况3下的位移云图，负号表示位移向下。工况3中有机玻璃面板的最大竖向位移绝对值为21.1mm，最大相对竖向位移绝对值为18.9 mm(图中最大位移减去最小位移)。三种工况下不锈钢杆件的最大von Mises应力分别为37.5，98.8，109.3MPa，均小于《不锈钢结构技术规程》(CECS 410—2015)[6]中规定的S31603不锈钢屈服强度(170MPa)。不锈钢支撑杆均承受压力(表2中负号表示受压)，轴力分别为6.2，18.3，20.4kN，该轴力值可作为支撑杆与有机玻璃连接节点的设计荷载。

3 影响因素分析

(1)温度作用

南京未来花园在设计使用年限内可能会受到其他因素的影响，如温度作用。如前所述，不锈钢支撑杆与有机玻璃肋之间采用滑动式连接节点，避免有机玻璃面板收缩或膨胀对整体不锈钢支撑结构的不利影响。但是，不锈钢结构本身也会有温度效应，因此需考虑温度变化对整体结构受力性能的影响。

按照结构降温40℃和升温40℃计算，暂不考虑荷载分项系数和组合值系数，本节单独考虑温度作用，不考虑其他荷载作用。计算结果见表3。从表3可以看出，由于支撑节点释放了径向自由度，在升温和降温过程中，有机玻璃肋上的von Mises应力和第一主应力的最大值变化非常小。降温时有机玻璃面板向下移动，升温时向上移动，这主要是由于不锈钢支撑的变形造成的。总体来说，温度作用对有机玻璃结构的影响较小。值得一提的是，本节未考虑温度作用对不锈钢结构应力的影响。本文的研究对象为单个树状结构，而实际上，南京未来花园的42个树状结构的不锈钢支撑是连在一起的，因此，当升温和降温时不锈钢结构会受到相邻连接结构的影响。

图5 有限元计算结果(工况3)

图6 连接节点

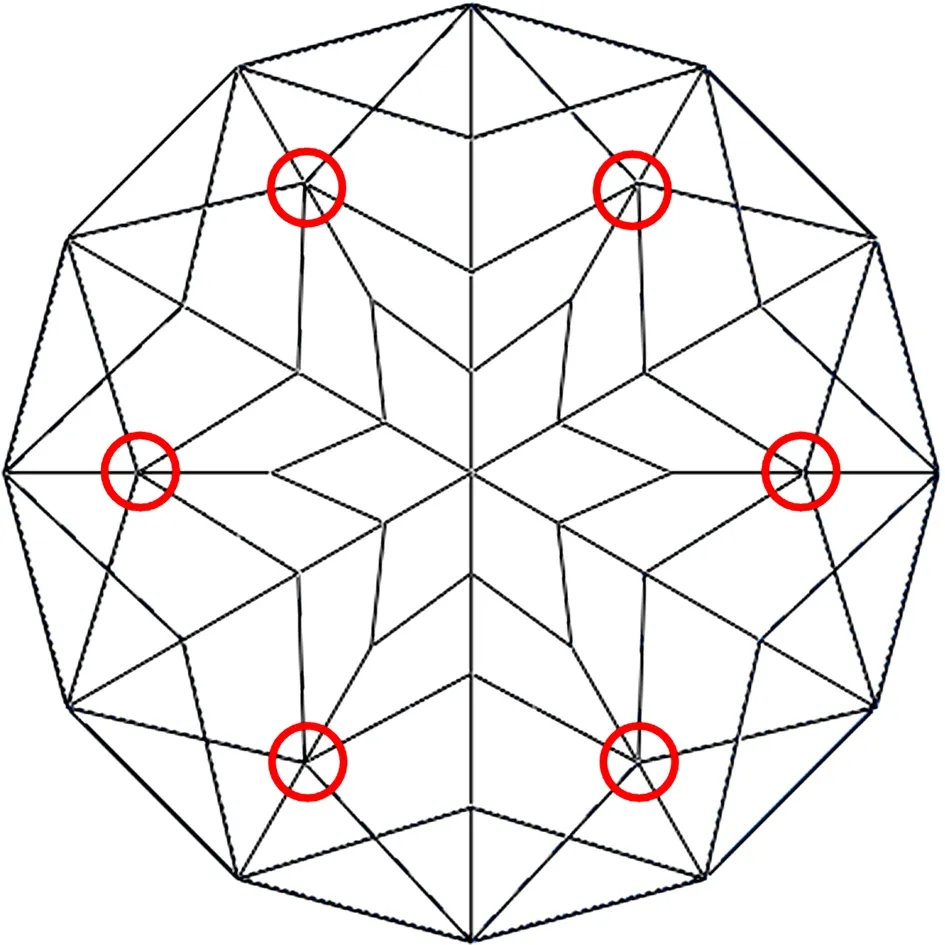
图7 轴力最大的支撑杆对应的节点

图8 节点失效时降温40℃对结构的影响

温度作用分析结果(最大值) 表3

(2)节点失效

有机玻璃的线膨胀系数较大，为了防止温度应力较大，南京未来花园设计了滑动式支撑节点,但可能由于安装误差等其他因素导致节点无法正常滑动。本节研究了支撑杆轴力最大处的节点在无法正常滑动的情况下，降温40℃对结构的影响。由2.2节的计算可知，图7中圈出的6个节点处支撑杆轴力最大。因此，在本节的模型中，这6个节点无法滑动。同样，本节不考虑其他荷载作用，因此计算出的应力结果可视为该因素作用下应力的增量。

从图8的计算结果可以看出，由于6个节点失效(无法滑动)，降温40℃时有机玻璃肋的第一主应力为2.3MPa，增幅并不是很大，有机玻璃仍然比较安全。但是，失效节点处的支撑杆应力非常大，已经达到了材料屈服强度。由于本文中不锈钢的本构采用的是理想弹塑性模型，因此应力达到了计算的最大值。除了这6个支撑杆之外，其他的不锈钢构件应力较小。实际上，在设计中预留了一定的空间，若发生了节点失效，可更换失效的杆件。

4 地震作用分析

对南京未来花园单个树状结构进行地震作用分析。工程所在地区的抗震设防烈度为7度，设计基本地震加速度为0.1g，设计地震分组为第一组，场地土类别为I1，特征周期为0.25s，考虑多遇地震作用下的影响，水平地震影响系数最大值为0.08[11]。根据规范要求，结构重力荷载代表值取结构自重标准值与有机玻璃面板上方水重量之和。水压视为活荷载，组合值系数取1.0。在地震分析中，忽略面板局部变形导致的附加水压，水面高度取为100mm。

首先进行模态分析，取模型的前10阶模态，得到各阶模态对应的频率值。节点的前4阶振型见图9，对应的自振频率分别为：0.177，0.351，0.351，0.970Hz。第1阶振型为扭转，第2阶振型为有机玻璃面板沿与X轴成135°夹角方向的平动带动结构整体转动，第3阶振型为面板沿与X轴成45°夹角方向的平动带动的转动，第4阶振型为面板绕X轴方向的转动。由计算结果可知，单个树状结构刚度较小，第1阶就出现扭转振型。

图9 结构前4阶振型

进行反应谱分析时，考虑扭转藕联现象，使用完全方根组合CQC法对各阶地震作用效应进行组合。结构阻尼比取0.05。多遇地震作用效应计算结果见表4。可以看出，水平地震作用对结构受力性能影响非常小，只会在一定程度上影响结构的位移。

水平多遇地震作用效应(最大值) 表4

5 结论

(1)有限元计算结果表明南京未来花园有机玻璃结构最大应力均位于肋上；在最不利工况下，有机玻璃肋的最大第一主应力小于3.5MPa，最大von Mises应力为3.79MPa，位于节点处。在实际工程中，节点区有机玻璃受力面积会加大，应力会降低。不锈钢的最大应力为109.3MPa，处于弹性状态。支撑杆最大轴力为20.4kN。

(2)采用滑动式支撑节点可较好地释放有机玻璃面板温度作用，温度变化对结构受力性能影响较小。

(3)当轴力最大的6个支撑杆对应的节点失效(无法滑动)时，有机玻璃肋的第一主应力增大2.3MPa，变化并不是很明显。但是6个支撑杆上的von Mises应力非常大，达到了材料屈服强度。实际工程中，若发生节点不锈钢支撑杆失效，可及时更换杆件。

(4)单个树状结构刚度较小，受水平地震作用影响较小，地震作用可不参与荷载组合。