不完全车联网环境下元胞自动机换道模型研究
2021-06-23于泽浩郑国荣刘小明尚春琳董路熙秦利南
于泽浩, 郑国荣, 刘小明, 尚春琳, 董路熙, 秦利南
(北方工业大学城市道路交通智能控制技术北京市重点实验室, 北京 100144)
0 引言
随着车联网技术的不断发展,在未来几年内将有一部分可实现自动驾驶功能的汽车加入交通行驶队列中,这将大大缓解目前交通拥堵等问题. 但要实现道路内的车辆全部自动驾驶,还有相当长的路要走,故对联网的自动驾驶车辆与未联网的普通车辆所组成的混合交通流进行研究意义重大,这是实现完全意义上的车联网之前的必经之路与先决条件. 构建交通流模型是研究交通问题的基本手段,因交通系统本身具有离散性和非线性的特点,元胞自动机模型成为交通流研究的重要工具.
元胞自动机交通流模型主要包括跟车模型与换道模型. 在换道模型研究中,1997年,Chowdury[1]建立了STCA模型,加入双车道换道规则,并被不断拓展与研究;王永明等[2-3]考虑驾驶员不同的驾驶特性,建立了更为灵活的换道条件,研究了不同换道条件对交通流的影响;刘小明等[4]考虑不同换道车辆换道意图,将模型细分为自由换道以及信息交互式换道模型;邓建华等[5]提出了内外因子共同影响换道决策的元胞自动机模型,具有良好的延展性;Tian等[6]研究了各种流行的交通元胞自动机模型,完成了单车道和双车道模型的分类和评价;Zheng等[7]基于BL-STCA模型,构建了考虑动态换道概率的改进双车道元胞自动机交通模型.
近年来,随着车联网技术的发展,自动驾驶车辆的交通流模型得到了人们的广泛关注. 朱艳玲等[8]考虑了车辆间信息交互作用,将鱼群效应引入车辆换道模型中,满足了车辆换道的及时性需求;赵雪圻等[9]分析了未加入自动驾驶车辆与加入自动驾驶车辆不同情况下的元胞自动机模型行驶特点;王文等[10]考虑了换道行为的多车道元胞自动机模型,探求了不同自动驾驶车辆比例对于交通流的影响;张腾[11]提出了一种基于车联网信息的智能车换道方法. 上述研究对于探究车联网环境下的交通流运行特征等具有较为重要的意义.
综上所述,对于元胞自动机换道模型的研究重点多以普通车辆行驶过程,或以完全车联网环境下的自动驾驶车辆为主,鲜有对于联网车辆与普通车辆所组成的混合交通流元胞自动机换道模型的研究. 因此,考虑车联网中自动驾驶车辆的行驶特点,在已有元胞自动机交通流换道模型的基础上进行改进,考虑自动驾驶车辆信息获取物理区间对于换道决策的影响,提出一种不完全车联网环境下的元胞自动机换道模型,在保证安全换道的前提下,进一步分析了车联网自动驾驶车辆比例与自动驾驶车辆关注区间等参数变化,对于路网交通流的影响,并通过数值模拟验证了改进模型的有效性.
1 不完全车联网元胞自动机交通流换道模型
在已有的元胞自动机换道模型中,往往只考虑了换道时刻车速的提高,未能从不同车道前方车辆总体通行效率上考虑,可能会导致换道车辆在换道后一段时间内速度出现减小,若车速受到抑制再次换道,常造成乒乓换道现象等. 针对上述情况,当交通流中存在一定数量的自动驾驶车辆时,自动驾驶车利用传感器进行道路环境感知,决策系统可根据采集到的外界环境信息进行换道规划,能够更加有效地利用道路资源,同时也避免乒乓换道的现象发生. 基于上述考虑,本文提出了一种不完全车联网环境下考虑关注区间的元胞自动机换道模型.
1.1 自动驾驶车辆关注距离及换道方法优化
假设道路中行驶的自动驾驶车辆可以根据车载终端与路侧单元等获取其他自动驾驶车辆与邻近普通车辆的车辆速度与位置信息,设置变量LS为自动驾驶车辆关注区间.本文定义LS为自动驾驶车辆执行换道决策时需考虑的前方距离范围.自动驾驶车辆在换道前不仅要考虑前方是否有低速车干扰和相邻车道的行驶条件,而且需要考虑LS内车辆所在车道与相邻车道车辆通行速度,保证换道后车辆是否可以在较长时间内保持较理想的速度行驶.关注区间LS如图1所示.

图1 自动驾驶车辆的关注距离LS
自动驾驶车辆不断检测LS内所在车道和相邻车道的自动驾驶车辆车速情况,若车辆的关注区间LS内相邻车道平均车速优于换道车辆所在车道的平均车速,则说明车辆若继续在所在车道行驶,速度可能会受到抑制,并不能按照理想速度提升,此时可在符合换道条件的情况下进行换道.
换道车辆所在车道关注区间内的自动驾驶车辆在时间步k的平均速度:
(1)
同理得到LS内相邻车道自动驾驶车辆在时间步k的平均速度:
(2)
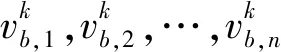
考虑关注区间内各车道自动驾驶车辆运行情况,建立换道模型如下.
If车辆满足dn
Cn=Cn-1;
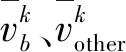
End
End
式中:dn代表第n辆车与前车距离;dn,other代表第n辆车与相邻车道前车距离;dn,back代表第n辆车与后车距离;dsafe代表安全间距.Cn=0或1,为车辆目前所在车道.
1.2 不同换道环境下的规则优化
模型中,车辆随机分布在元胞上,元胞有空闲或被车辆占用2种状态.其中,vn(t)为第n车辆在t时刻的速度,Xn(t)为第n辆车在t时刻的位置.其中速度vi=[0,vmax] (Vmax=5为车辆在模型中的最大行驶速度,速度在这里取整数).
演化规则上有:
1)车辆加速状态:vn=min{vn+1,vmax};
2)车辆减速状态:vn=min{vn,dn};
3)车辆随机慢化:以P的概率随机减速,vn=max{vn-1,0};
4)车辆位置更新:Xn=Xn+vn.
在图2所示的换道环境下,驾驶者期望以路段的最高速度行驶,在无前方车辆干扰的情况下不进行换道或减速行驶;而在原有的STCA模型中若0车道的A车在某一时刻受到了慢车B的干扰,A车可以选择进行换道,但换道条件规定:若换道到1车道后:C车与A车的距离要大于dn,back,但dn,back设置过大,影响了道路使用效率. 若A车速度较快,C车速度较慢,即使换道完成,C车也不会与A车发生追尾,反而距离变大,则这样的换道约束较为苛刻,不符合提高车速的需求,也会对道路资源造成了极大的浪费.
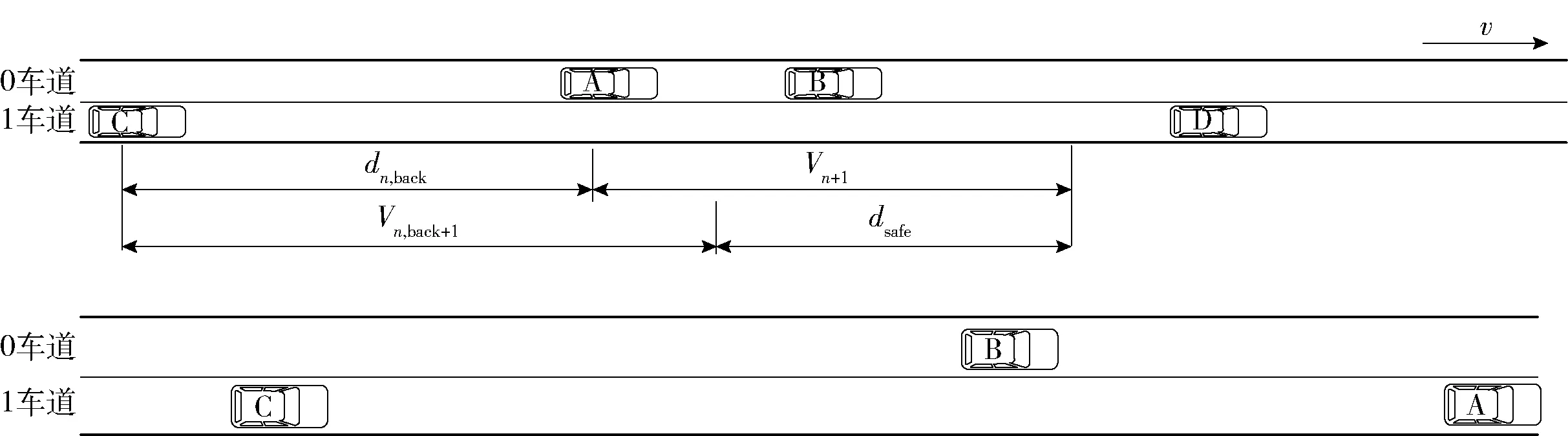
图2 换道场景
在行驶过程中,自动驾驶车辆通过速度指标进行对比,判断换道是否有利于车速提升.在换道动机(dn
由于自动驾驶车辆的加入,根据换道车辆及目标车道后车的类型不同,车辆在换道时与后车的安全距离dsafe也会发生变化,主要有4种换道情况:
1)换道车辆与相邻车道后车均为自动驾驶车辆;
但是我终于出来了。我越过那堆积着像山一样的十八年的长岁月,回到了生我养我而且让我刻印了无数儿时回忆的地方。我走了很多的路。
2)换道车辆为普通车辆,相邻车道后车为自动驾驶车辆;
3)换道车辆为自动驾驶车辆,相邻车道后车为普通车辆;
4)换道车辆与相邻车道后车均为普通车辆.
在情况1)下,因为换道车辆与相邻车道后车均为自动驾驶车辆,相邻车道后方的自动驾驶车辆可根据换道车辆的速度与换道意图,调整自身车速,为换道车辆成功换道提供条件.同时自动驾驶车辆通过速度的调整,使前后车速度更加接近、间隔更小,形成两车编队行驶,更少地占用道路资源.此时,在保证dsafe≥1前后车不追尾时即可换道.若在换道时还不满足dsafe的约束条件,则由相邻车道后车(自动驾驶车辆Cback)进行速度调整满足下一时刻的换道条件,即:
dn,back+min{vn+1,vmax}=min{vn,back+1,vmax}+dsafe
令dsafe≥1则有:
dn,back+min{vn+1,vmax}-min{vn,back+1,vmax}≥1
再次转换得出:
min{vn,back+1,vmax}≤dn,back+min{vn+1,vmax}-1
故自动驾驶车辆将车速调整为小于等于dn,back+min{vn+1,vmax}-1即可.
在情况2)下,也由自动驾驶车辆进行速度调整,速度变换与情况1相同.
在情况3)下,自动驾驶车辆通过调整自身速度,在保证车辆可进行安全换道且不会因变道而导致速度下降的前提下进行换道调整,即:
min{vn+1,vmax}≥1+min{vn,back+1,vmax}-dn,back
换道后自动驾驶车辆可作为后方普通车辆的头车进行编队行驶,通过自身对于速度感知的敏感性,对后方车辆进行一定的速度引导.
在情况4)下,普通车辆则按文献[2]中STCAII中规则进行换道.规则如式(3):
(3)
由于换道的目的是为了追求更高的速度行驶,故换道车辆在执行换道动作时,令减速概率P=0.
2 数值模拟
将本文的改进模型与STCA模型、文献[2]中的SCTAII模型进行仿真比较. 自动驾驶车辆根据优化方式行驶和换道,普通车辆按照STCAII方式行驶. 具体参数如表1所示(为消除初始暂态对实验的影响,对仿真中的前5 000个时间步数据不做统计,并采用周期性边界条件).
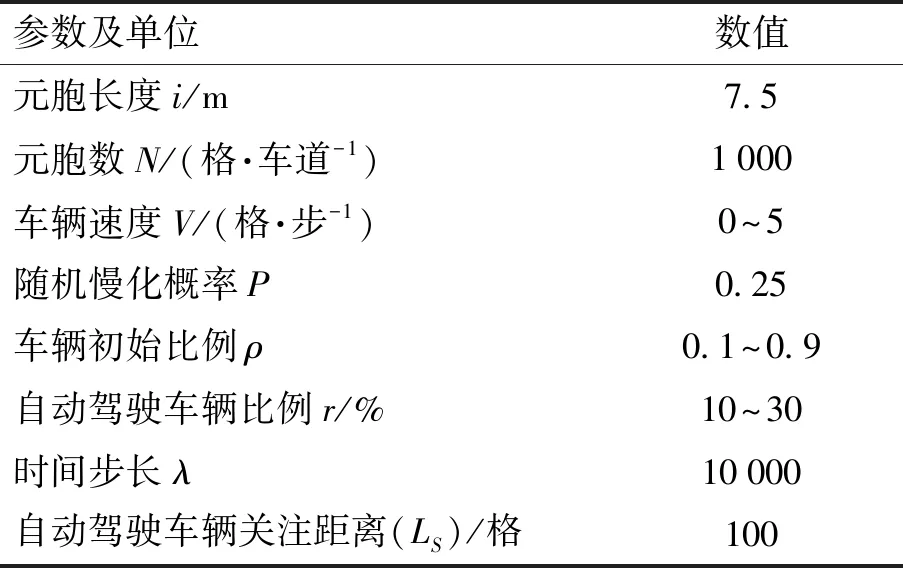
表1 仿真参数选择
2.1 平均速度分析
通过改变路网中车辆密度,自动驾驶车辆比例设置为车辆总数的10%、20%与30% 3种观察不同行驶环境下车速变化情况. 选取STCA模型和文献[2]中的STCAII模型进行对比. 具体效果对比如图3所示,其中横坐标为路网中总体车辆密度(单位:辆·格-1),纵坐标为路网中车辆的平均速度(单位:格·s-1).
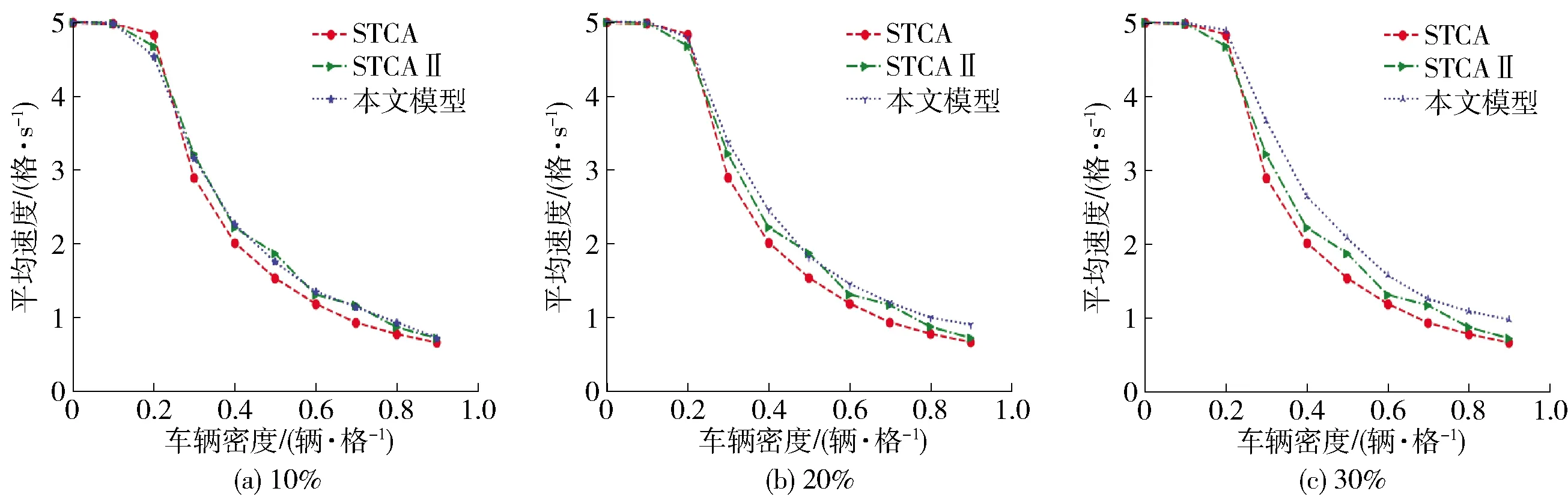
图3 自动驾驶车辆不同比例时平均速度与车辆密度关系图
从图3数值模拟结果对比来看,在车联网车辆比例一定时,随着车辆密度的增长,各模型速度呈逐渐减低的趋势. 在车辆低密度较低时,各模型平均速度几乎相同,但随着车辆密度增长至0.3辆·格-1左右时,与STCA模型和STCAII模型相比,本文模型的优势逐渐显现,这是由于车辆密度的提高意味着道路资源的紧张,由于换道条件的改善,提高了车辆的平均速度. 从图4的纵向对比来看,在车辆密度不变的前提下,随着自动驾驶车辆比例的增加,平均速度也有所增加. 同时,由于车辆密度的增大,车辆行驶空间在逐步变小,车辆速度不可能无限制的增大,故道路中车辆平均速度一般在3格·s-1左右上下浮动.
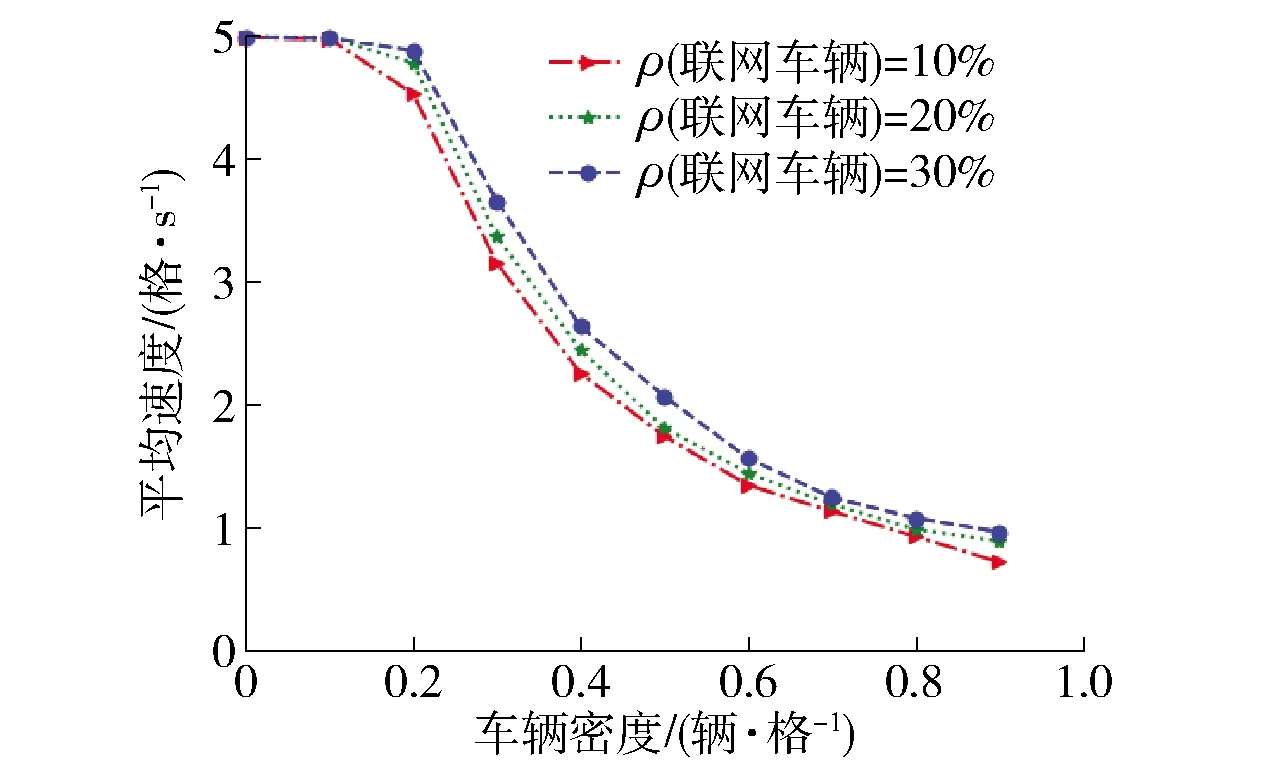
图4 不同自动驾驶车辆密度下平均速度对比
进一步分析,通过改变Ls的大小,比较不同情况下道路上车辆平均速度,由图5可以得知,随着Ls的不断增大,道路车辆的平均速度呈现上升趋势,这是由于自动驾驶不仅考虑了换道时刻速度的变化情况,也考虑了车辆感知距离内平均速度等因素,在基于整体最优的前提条件下进行换道调整,使速度得到提升.
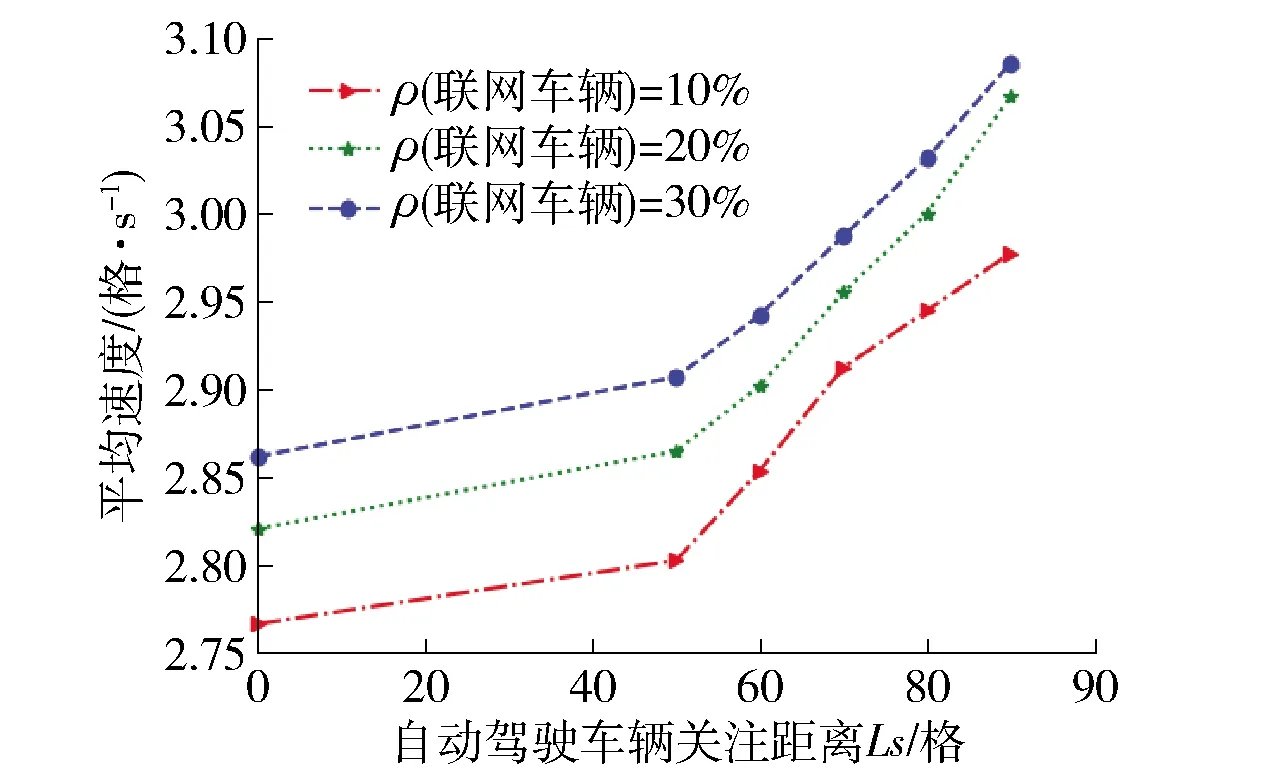
图5 不同Ls下的车辆平均速度
2.2 换道频率分析
换道意味着速度的提升,故换道频率也是考察模型效率提升的重要指标之一. 图6为自动驾驶车辆比例为10%、20%与30% 3种情况下不同行驶环境换道频率的变化情况.
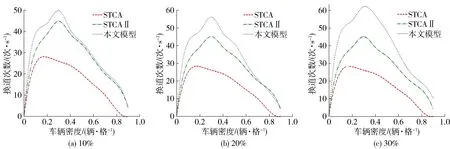
图6 自动驾驶车辆不同比例时换道频率与车辆密度关系图
在相对车辆低密度区,自动驾驶车辆比例一定时,换道频率随着车辆密度的变化而增加,这是由于道路资源相对充裕,受低速车辆限制的高速车辆换道机会较多,因而换道频率提高,侧面说明了车辆速度的提升. 由于在STCA模型中对于换道条件的要求比较苛刻,故换道频率相对较低. 据图7纵向对比来看,随着自动驾驶车辆比例的不断增加,虽然关注区间内车辆所在车道和目标车道的平均速度比较,在一定程度上限制了车辆的换道,但由于车辆信息交互增加以及换道安全距离的变化,最终使得换道次数也在增加,有更多的车辆可获得更高的速度.
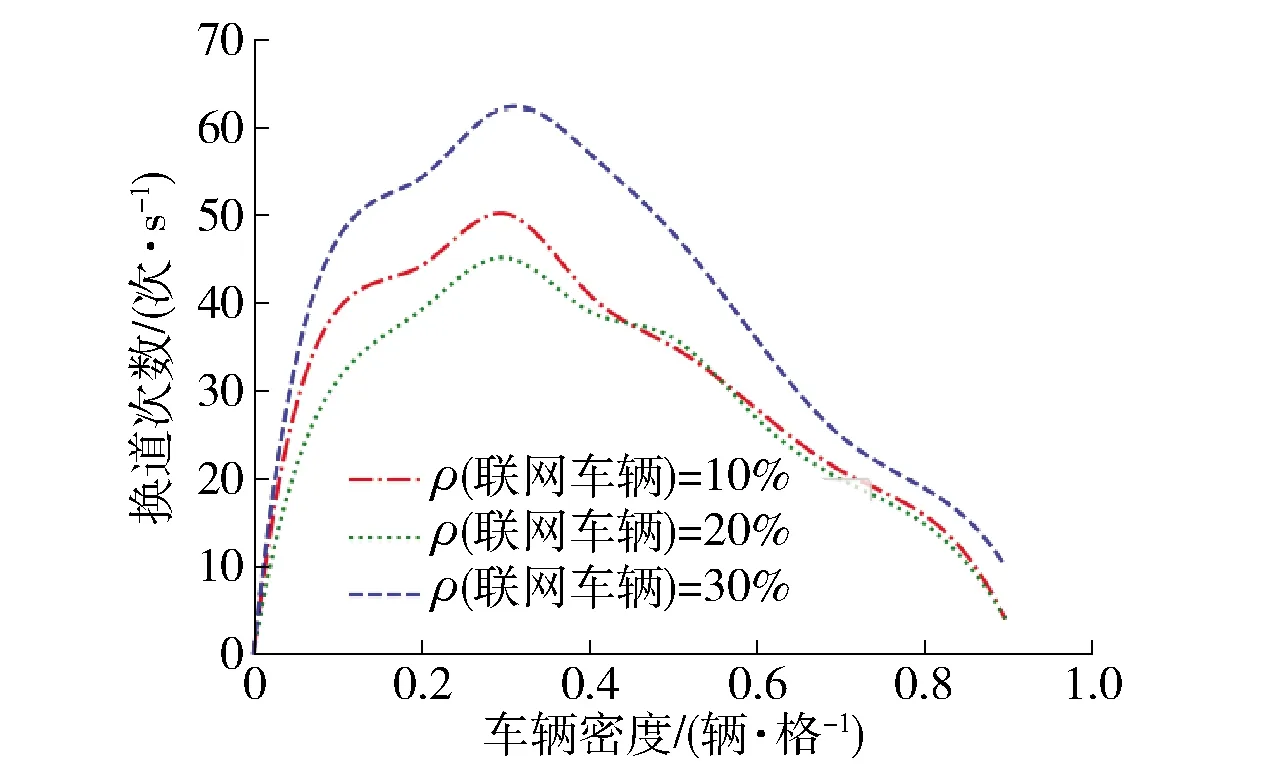
图7 不同自动驾驶车辆密度下换道频率对比
2.3 流量分析
3种改变路网中车辆密度,再将自动驾驶车辆比例设置为占总车辆数的10%、20%与30%,观察不同情况下车辆在不同行驶环境下流量的变化情况. 具体效果对比如图8所示.
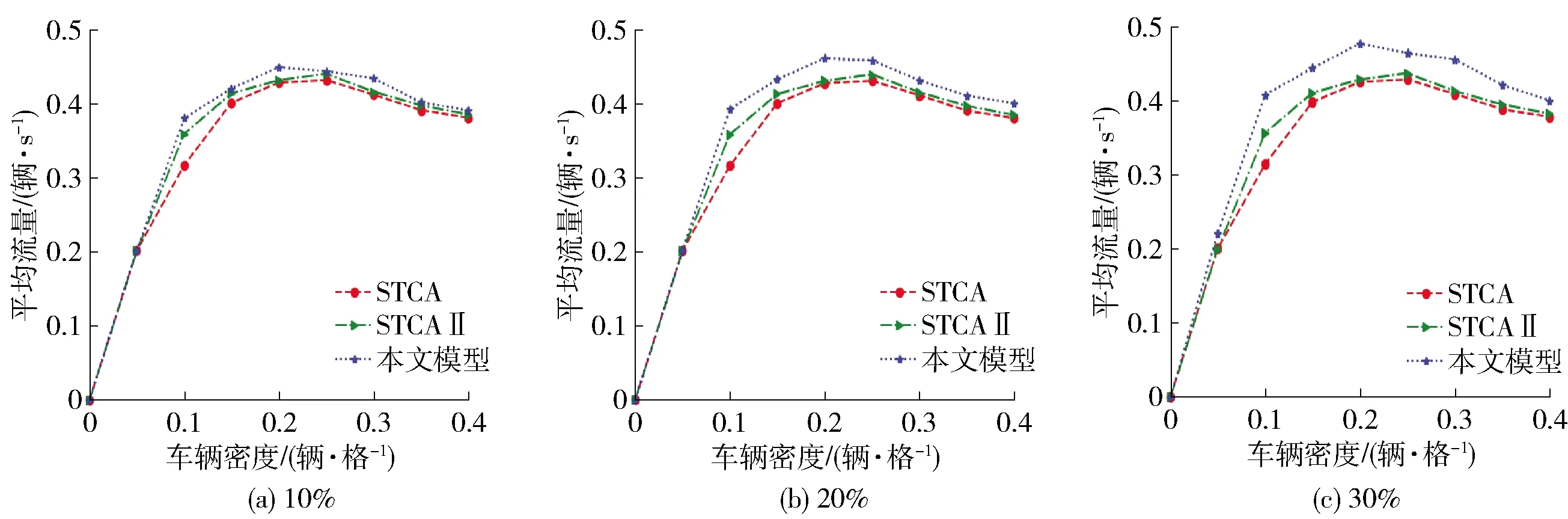
图8 自动驾驶车辆不同比例时平均流量与车辆密度关系图
根据交通流特性可知:在密度不变的情况下,流量与速度成正比. 由图8也可知,当速度提高时,优化模型的平均流量也有所提升,在元胞自动机模型中,车辆不可能无限靠近,必须保持最小一个格的安全间距,流量也不可能随车速的扩大而无限增大,流量随车速变化而变化,大体0.3~0.4辆·s-1之间. 在车辆密度较低时,车辆在被前方慢车阻挡运行时,可较为自由的换道,以充分发挥自动驾驶车辆优势,进一步提高道路车流量.
3 结论
本文通过提出自动驾驶车辆关注区间的概念,设计了不完全车联网环境下新型混合交通流元胞自动机换道模型,优化了原有STCA模型中复杂的换道条件,并进行了一系列的仿真实验. 结果表明:①新型混合交通流元胞自动机换道模型较STCA模型可以在保证安全换道的前提下,提升车流平均速度15%左右;②关注区间的设立,可从整体交通状态出发,避免车辆陷入单车车速最优或局部车速最优,有助于提升道路总体的通行能力.
