Mackey-Glass系统改进欧拉法的分支行为

姚洁怡， 王 琦

(广东工业大学 应用数学学院， 广东 广州 510520)

加拿大学者Michael C. Mackey[1]在20世纪70年代对生理系统的研究做了开创性的工作。此后，因为Mackey-Glass系统作为一个基础的生物学例子，对生理调控也有一定的指导意义，其动力学性质受到越来越多的关注[2-4]。许多学者将他们的研究集中在Mackey-Glass系统的分支、混沌等动力学行为上。实际上，对于具有任何参数的时滞非线性动力系统，当时滞增加超过某个临界值时都可能导致系统从稳定平衡变得不稳定，并导致分支。不同时滞下的稳定域如何变化？分支发生时如何确定时滞的临界值？质量行为如何依赖于时滞的形式？这些问题促使我们研究时滞变化对系统动力学行为的影响。考虑到科学计算和实时仿真的需要，我们的兴趣集中在原系统对应的离散动力学系统的行为上[5-9]。在大多数情况下，希望由微分方程导出的差分方程保持相应连续时间模型的动态特征。即离散时间模型与连续时间模型“动态一致”。Ford和Wulf[10]运用根轨迹法，证明了线性多步法的收敛阶与原时滞微分方程相同，其稳定区域收敛于原方程的稳定区域；2000年，他们又用欧拉法研究了一类带参数的时滞微分方程并且证明了离散格式与连续时间模型“动态一致”[11]。这意味着，对于所有足够小的步长，欧拉法离散模型经历与相应的连续时间模型相同类型的Hopf分支。

近年来，研究人员发现许多差分方法都是能够保持动态一致的。利用时滞τ作为参数，DING Xiao-hua等[12]应用梯形方法研究了Mackey-Glass系统的动力性。SU Huan等[13-14]用非标准有限差分方法研究了Mackey-Glass系统的Hopf分支的存在性与稳定性并且计算了分支方向，对Hopf分支的控制作了分析。然而，用改进欧拉法求解时滞微分方程的文献还很少，改进欧拉法能否保持时滞微分方程的动力性有待于研究。在本文中，利用改进欧拉法对Mackey-Glass系统进行离散，研究离散化后的系统在正平衡点处的稳定情况和Hopf分支存在性。

1 正平衡点的稳定性与局部Hopf分支

对于时滞微分方程

(1)

其中p(t)表示血液循环系统中t时刻成熟细胞的密度，τ是时间延迟，t≥0，β、θ、n、γ都是正常数。

令p(t)=θx(t)，方程(1)变成

(2)

这里a=β/θ，让u(t)=x(τt)，则方程(2)可以写成

(3)

下面将改进欧拉法应用于方程(3)，取步长h=1/m，令

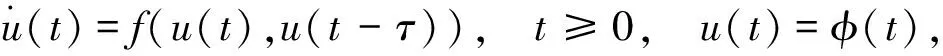
建立预报-校正系统

(4)

其中un=φ(nh)，-m≤n≤0，且

(5)

un为φ(nh)的近似值。用un-m来近似时滞项u(tn-τ)。

将式(5)代入式(4)，有

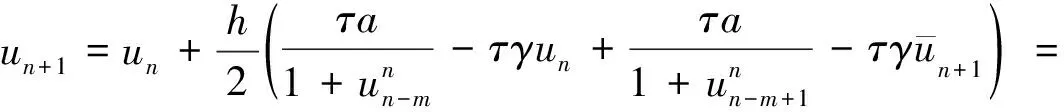
化简得到改进欧拉法递推格式

(6)

假设u*是方程的一个不动点，u*满足以下方程

γun+1+γu-a=0，

令

F(x)=γxn+1+γx-a，

对所有x≥0，F′(x)=(n+1)γxn+γ>0，F(0)=-a<0，故方程(1)有唯一正不动点u*。

让yn=un-u*，那么，有

(7)

引进一个新的变量

Yn=(yn,yn-1,…,yn-m)T，

那么存在一个映射

Yn+1=F(Yn,τ)，

其中

F=(F0,F1,…,Fm)T，

(8)

显然，原点是上式的一个不动点，并且它的线性部分为

Yk+1=AYk，

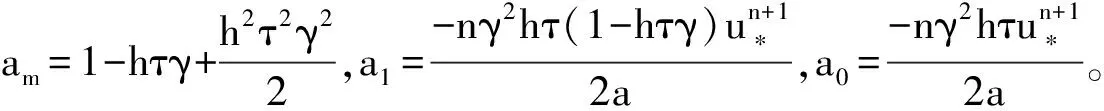
因此，A的特征方程为

(9)

引理1 对于充分小的正数τ，方程(9)的所有根都小于1。

证明当τ=0时，方程(9)等价于λm+1-λm=0，方程有一个m重根和一个单根λ=1。

考虑方程(9)的根λ(τ)，使得λ(0)=1，方程(9)是关于τ可微的，则有

(10)

(11)

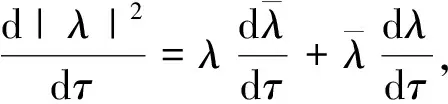
所以，随着τ>0，没有特征根穿过λ=1。因此，对于充分小的正数τ，方程(9)的所有特征根都在单位圆内。

随着τ的变化，当方程(9)出现一对共轭的特征根穿过单位圆时，Hopf分支产生。要证明Hopf分支的存在性，需要找到单位圆上ω的值。

用eiω表示单位圆上的根，则当ω∈(0,π]时，eiω是方程(9)的根，当且仅当

(12)

分离实部和虚部，有

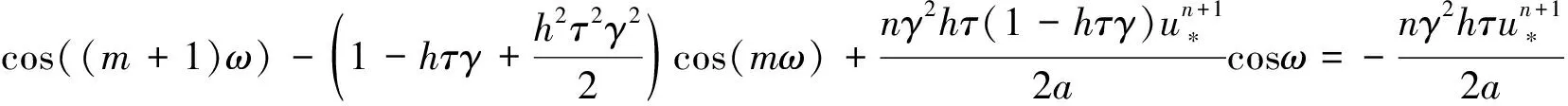
(13)

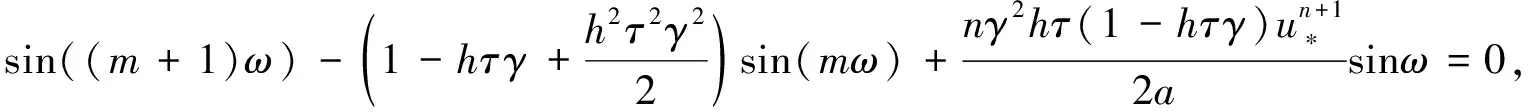
(14)

所以

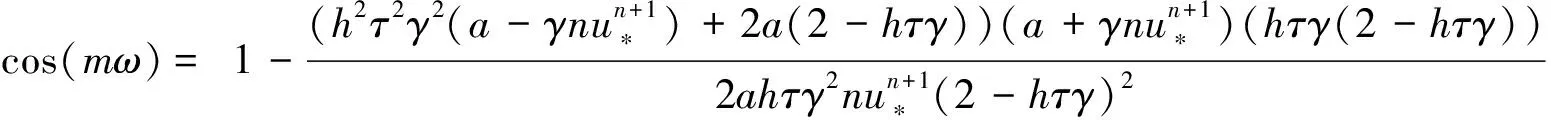
(15)

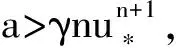
(16)

其中[·]为取整函数。

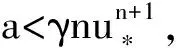
(17)

其中ωi满足方程(16)。

证明根据方程(14)和(15)，有

得证。

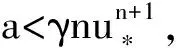
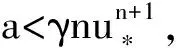
由引理4可得方程(9)零解的稳定性。所以关于方程(6)我们有如下定理。

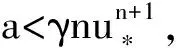
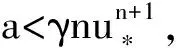
2 数值实验

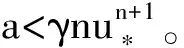
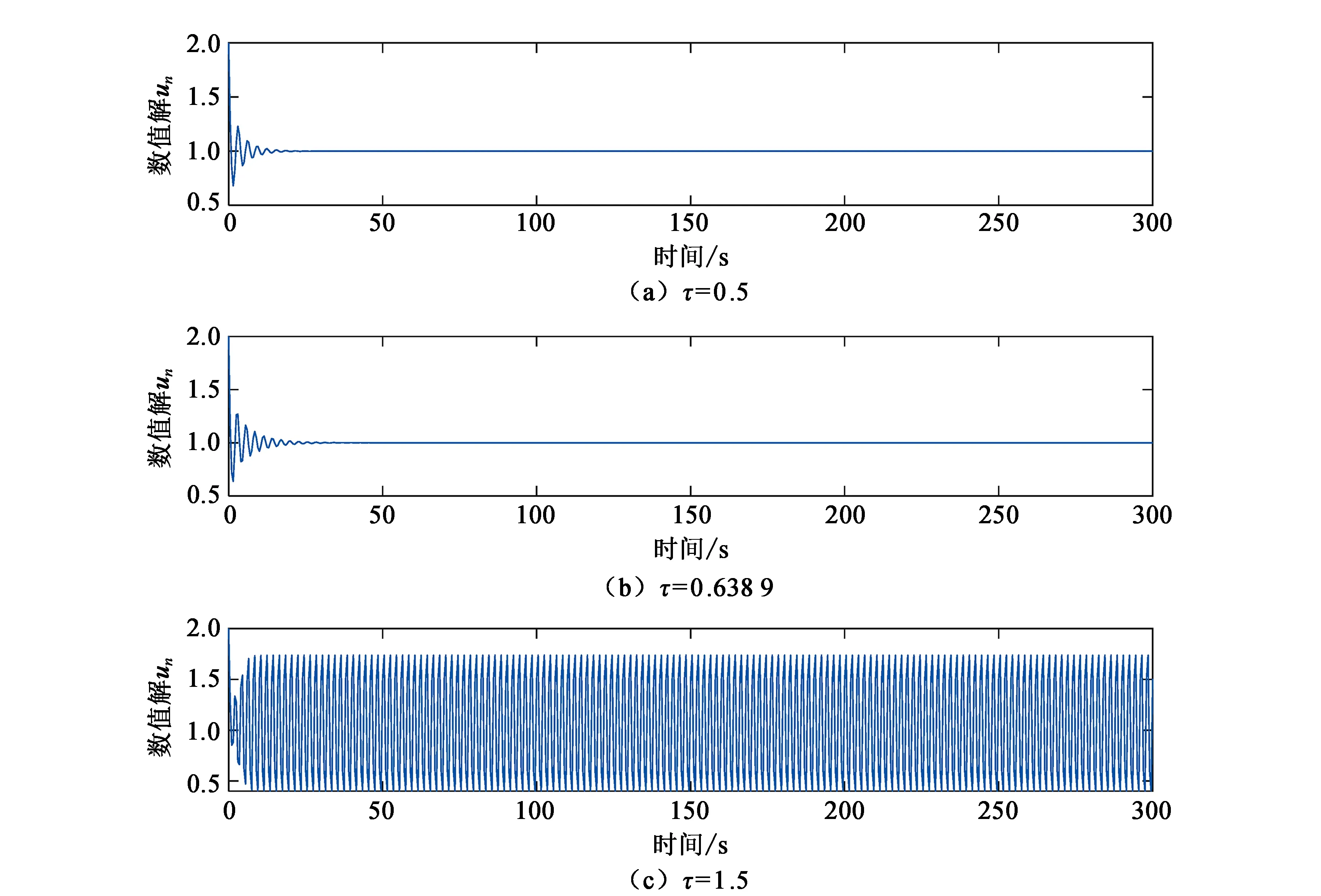
图1 步长h=1/2时方程(3)的数值解

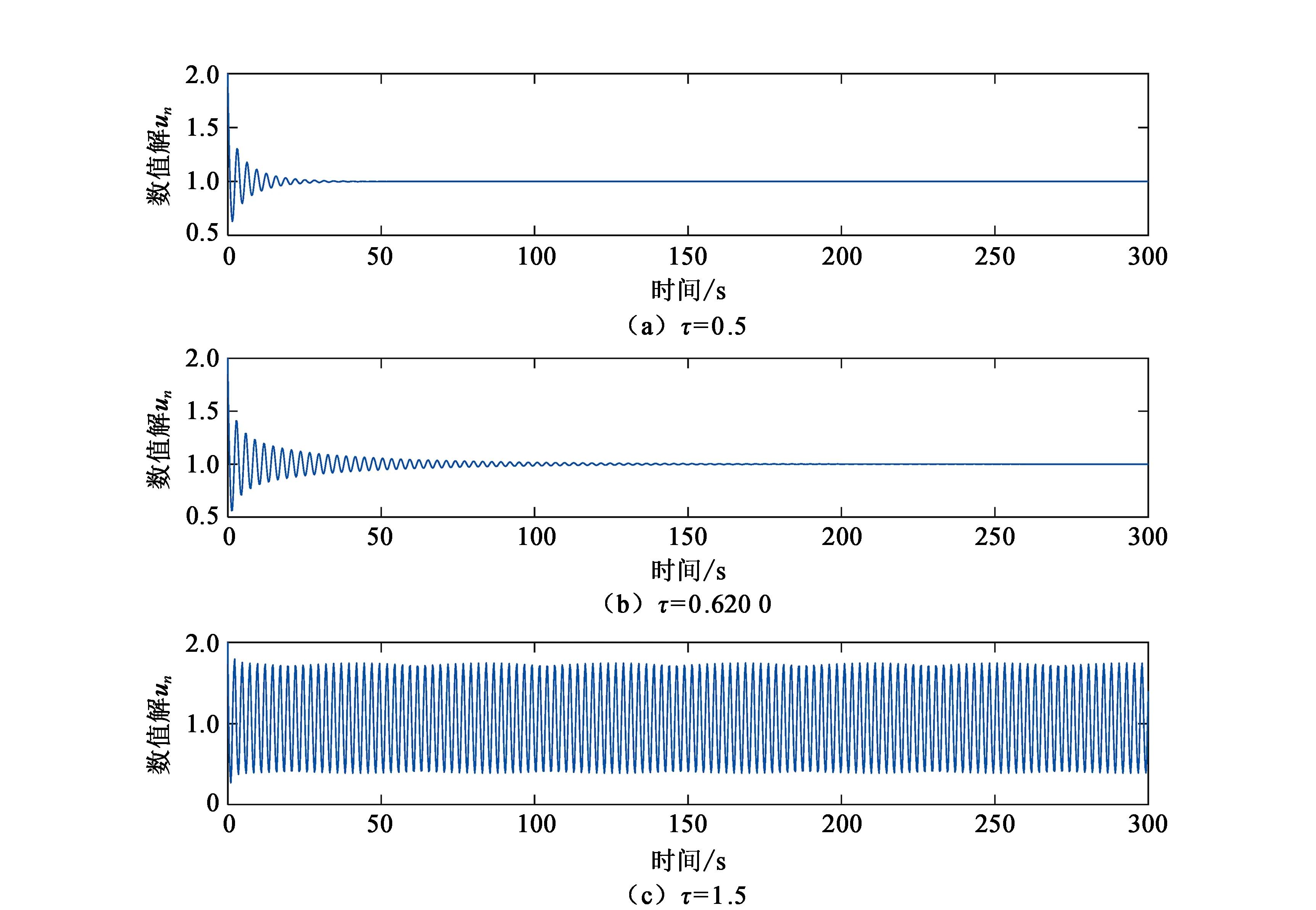
图2 步长h=1/4时方程(3)的数值解

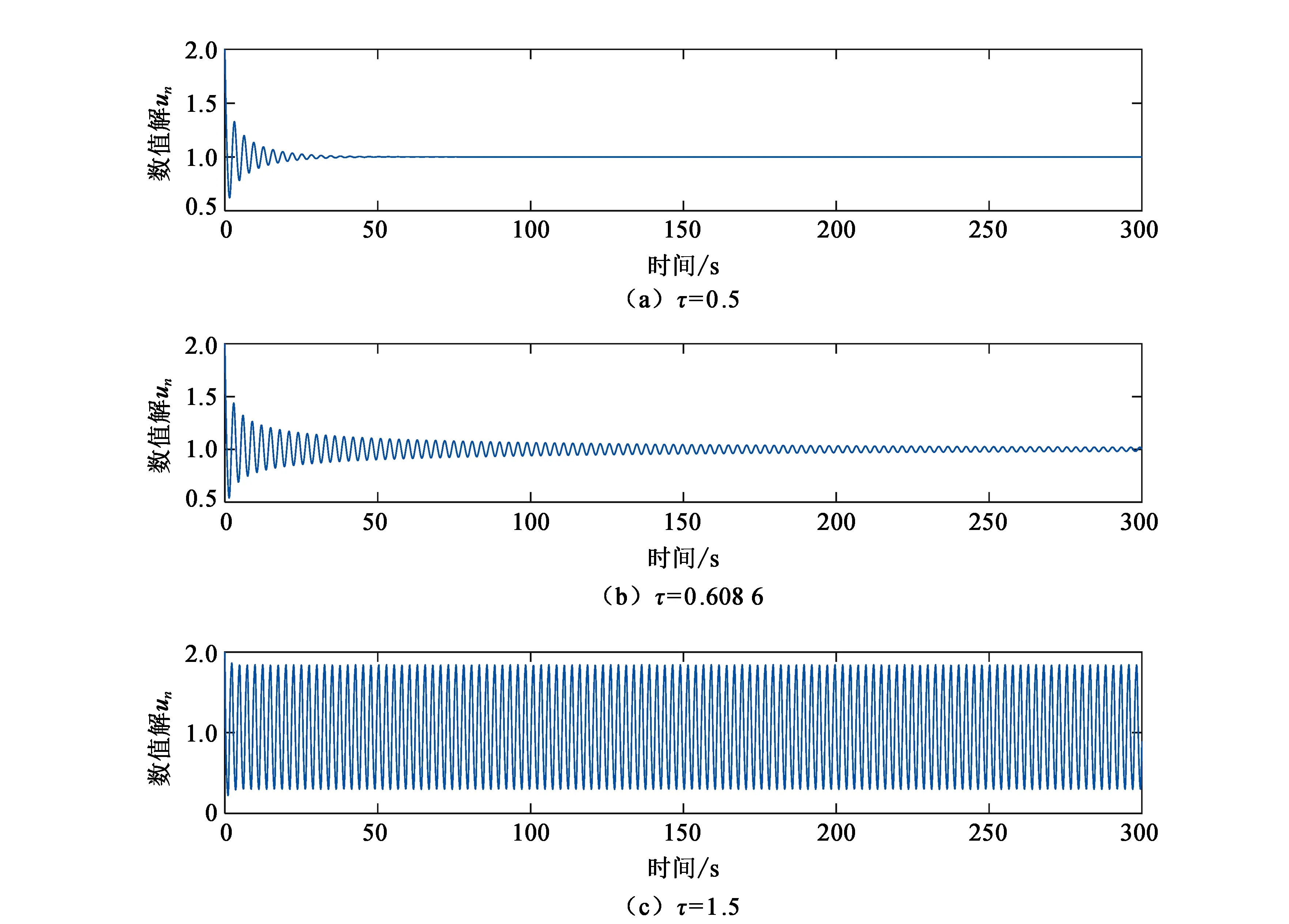
图3 步长h=1/8时方程(3)的数值解

根据定理1和表1，由图1—图4可见，当τ∈[0,τ0)时，方程(3)的数值解都是渐近稳定的；而当τ>τ0时，数值解不稳定。数值现象与理论分析结果是一致的。

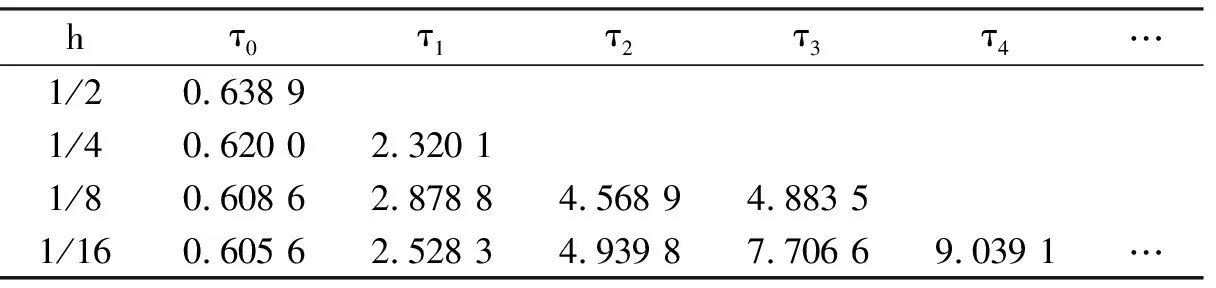
表1 不同步长下分支点的值

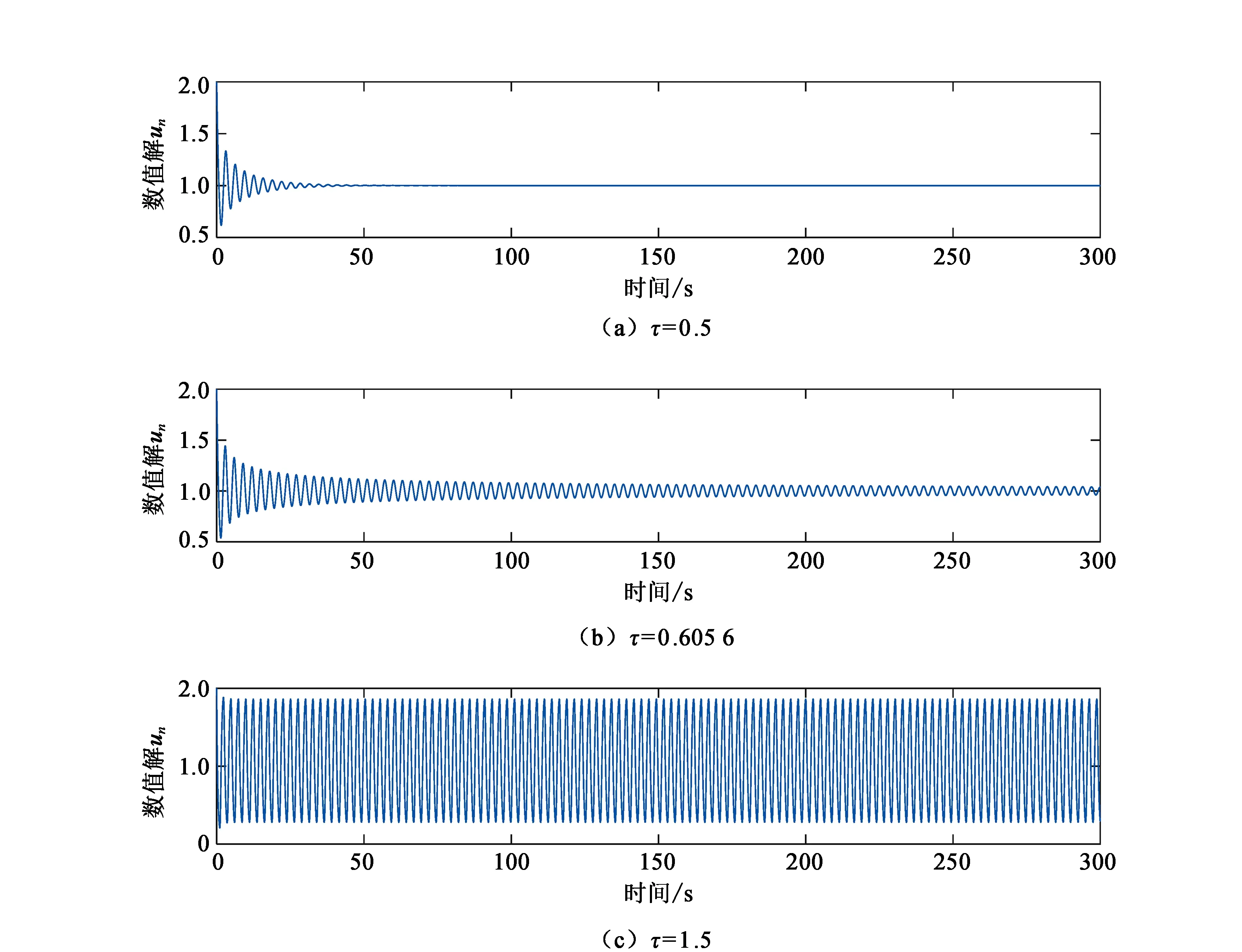
图4 步长h=1/16时方程(3)的数值解

3 小结

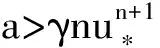
通过与文献[16]中给出的原系统状态图与动力学性质比较，改进欧拉法的数值模拟能够正确地反应原系统的动力学性质，即保持其动态一致性。