水润滑轴承电磁加载装置动态电磁力仿真分析

袁 哲， 王 楠,2*， 王 鹏,2

(1.陕西理工大学 机械工程学院， 陕西 汉中 723000；2.陕西省工业自动化重点实验室， 陕西 汉中 723000)

水润滑轴承作为水下最适宜的轴承，已广泛应用于船舶、水轮机等水力机械中，近年来成为研究热点。对水润滑轴承进行动态试验研究时，需模拟水润滑轴承工作环境以提高试验可靠性，其中对于载荷的模拟尤为重要，因此，必须对轴承加载装置进行设计与研究。

目前水润滑轴承的加载大都是传统接触式加载方式。例如，杜媛英等[1]设计了一种水润滑轴承的试验台，其加载方式为一轴承系统支撑采用液压进行加载；Kuang Fu-ming等[2]采用液压加载的方式对水润滑轴系加载；宋强等[3]设计了一种采用液压千斤顶的加载方式对水润滑轴系加载来分析水润滑轴承的参数特性；刘宗涛等[4]设计了有两套加载方式的水润滑轴系试验台，动态加载时激振器连接轻杆通过给定激振器不同信号频率对轴系进行加载，静态加载时通过滑轮、砝码、弹簧等装置进行加载；Shinde等[5]通过电机带动轻杆的机械加载方式，对水润滑轴承各种参数进行研究。

传统接触式加载方式存在噪声、振动、发热以及磨损等缺点，为解决上述问题，不少学者相继研究非接触式加载方式，其中电磁加载装置成为研究热点。郭一[6]利用一对C型电磁铁来对轴承进行加载并通过自适应动态面控制方法,引入低通滤波器有效消除反演设计存在的“微分爆炸”现象,实现未知参数的在线辨识。任正义等[7]设计了一种E形结构12磁极径向电磁轴承验证径向电磁轴承支承性能。Nevaranta等[8]介绍了一种八极式结构的电磁加载装置对转子轴系加载。王楠等[9-10]设计了一种用于对水润滑轴承进行模拟加载的非接触式电磁加载装置，并进行了水膜压力试验。

电磁加载装置研究中，动态加载时出现的电磁力随轴转速变化和不稳定等现象不可忽视，直接影响轴承试验测试过程与结果。针对上述问题，邱荣华等[11]利用U型磁铁对高速电主轴进行加载试验分析，得到了电磁力与转速变化关系，但未对电磁力动态变化影响因素进行深入分析。

为了确保水润滑轴承研究中电磁加载装置为轴承提供载荷的准确性与稳定性，需要深入研究电磁力动态变化机理。因此，本文针对已有电磁加载装置，通过理论、仿真相结合的方式分析动态条件下加载装置的可行性问题。

1 电磁加载装置及原理

电磁加载装置如图1所示，包括E型电磁铁、加载盘、线圈与底座。压力传感器安装在电磁铁正下方并固定在底座上，电磁铁分布在加载盘下方左右两侧、互成90°，电磁铁与加载盘之间气隙为2 mm，铁芯材质为纯铁。相对U型磁铁，E型磁铁加载面积更大，因此产生的加载力更大；导电线圈采用漆包铜导线，线圈缠绕在电磁铁内部铁芯上。图2为电磁加载装置电磁力分析图，轴承静态加载时，根据麦克斯韦理论，对线圈通入直流电流后，因气隙磁导率远小于加载盘磁导率，因此在气隙与加载盘的分界面将会产生电磁力F左、F右，且方向垂直于加载盘向外。当水润滑轴系转轴旋转时，加载盘表面产生涡流场，形成切向加载力f1、f2抵消部分气隙磁场，形成磁阻并产生电磁损耗。

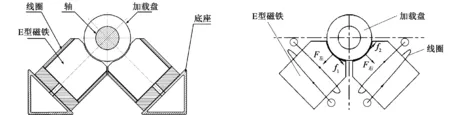
图1 加载装置结构 图2 电磁加载装置电磁力分析图

为在气隙磁场不变的情况下产生较大的径向电磁力，防止自感和互感现象消失从而导致线圈失效，加载盘应选用具有良好导磁率的磁导材料以及磁饱和强度大的材料。通过对比各种材料(纯铁、铁基非晶、硅钢片等)，并结合实际情况以及成本考虑，加载盘材料选用硅钢片。

2 动态加载力理论模型

研究水润滑轴承加载装置的动态特性时，相对于静态需要考虑多种因素：涡流效应、非线性磁导率以及漏磁等，根据Maxwell方程组并结合实际情况，通过物质方程可以得到磁场强度H和磁通密度B的关系、电流面密度J和电场强度E的关系，得到水润滑轴承在旋转电磁场中磁通密度的二阶偏微分方程：

(1)

根据图1所示水润滑轴承电磁加载装置，建立其解析模型。在轴旋转时，NS极不断交替，从而产生交变磁场，轴上的加载盘会产生涡流效应和集肤效应。动态理论模型的求解极为复杂，因此求解条件需要做一定的假设和简化：加载盘材料(硅钢片)与E型磁铁材料(纯铁)都具有很高的导磁率，因此可忽略气隙中漏磁、磁饱和磁滞效应的影响;在交变磁场中集肤效应远小于加载盘直径，因此加载盘运动模型展开如图3所示;加载盘可看作为半无限大的导电平板在磁极下做水平运动。

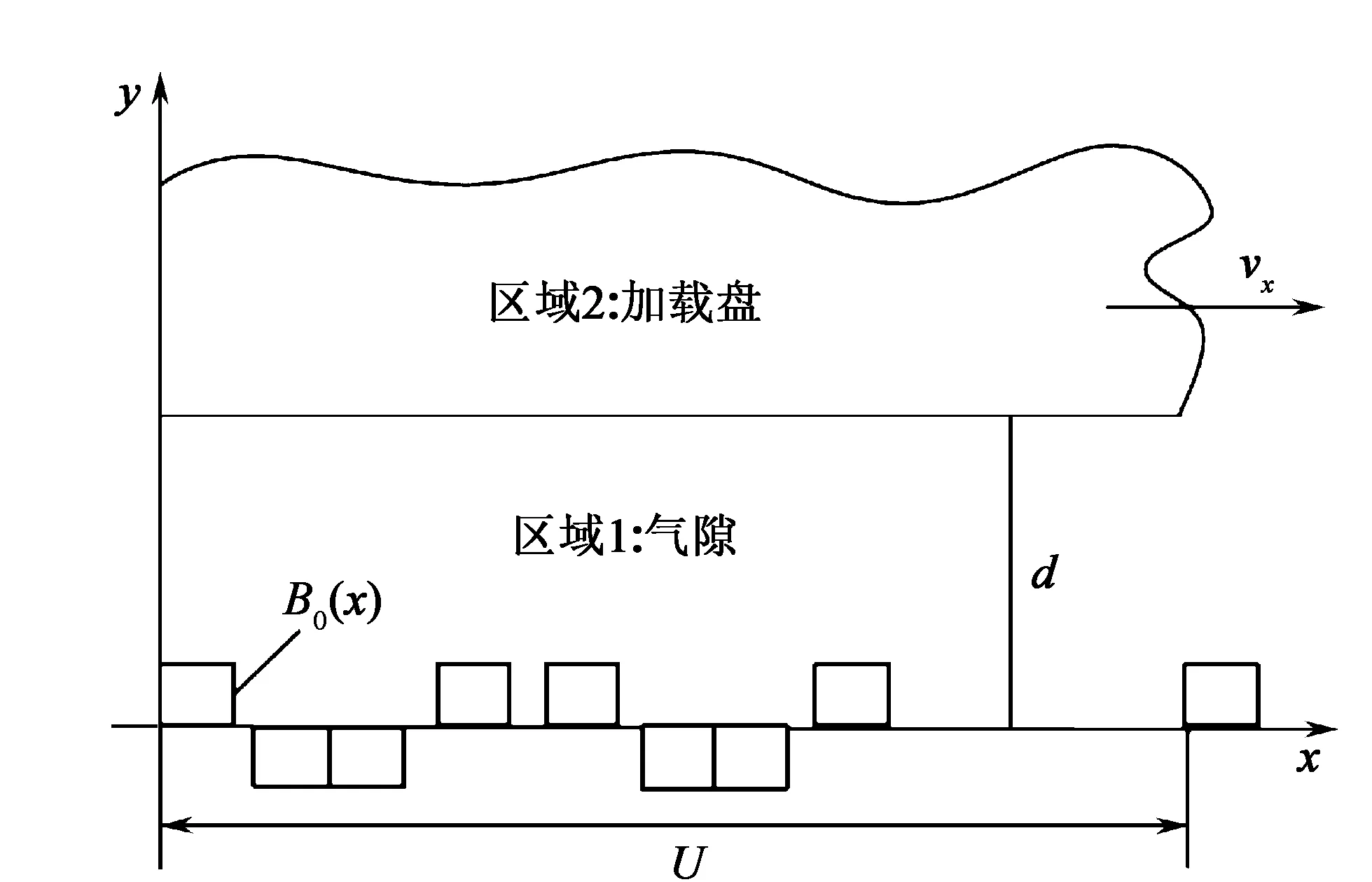
图3 展开的加载盘运动模型

图3中，U为加载盘外圆周长，d为气隙厚度，vx为加载盘的平均速度，B0(x)为加载盘表面的磁通密度。由图3可知，磁感应强度在x、y方向上的分量分别为Bx、By，电流沿z轴方向、加载盘沿x轴方向运动。最后得到的径向电磁力计算公式为[11]

(2)

经积分展开得

(3)

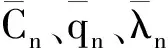
为研究水润滑轴承在旋转时转速、电流与电磁力的关系，对上述方程进行数值计算，部分参数如表1所示。

表1 数值计算部分参数

3 加载装置有限元仿真

采用Ansoft Maxwell 18.2进行电磁加载装置三维仿真，得到不同电流和转速条件下加载盘的径向电磁力。针对实际电磁加载的尺寸参数，通过Solidworks 2016得到加载装置的三维物理模型，如图4所示。将得到的物理模型导入到Ansoft Maxwell 18.2，设置求解类型为瞬态磁场(Transient)。

根据实际加载装置材料，需指定图4模型材料属性：加载盘-硅钢片,E型磁铁-纯铁,线圈-铜(copper)。加载盘由一片片硅钢片叠压而成，材料编辑时选择Lamination项。z轴为叠压方向，线性。瞬态场仿真需对旋转部分即加载盘添加band域，在band域中添加所需转速。三维瞬态场中，选取边界条件为Zero Tangential H Field，该边界磁场强度切向分量恒为0。线圈匝数为915匝，绕组类型为Stranded(绞线型绕组)，电磁铁分布在加载盘下方左右两侧、互成90°，串联方式，故并联支路数为1，电流为1 A。Ansoft Maxwell静态场仿真的网格划分具有自适应性，而瞬态场仿真网格划分需手动剖分。三维网格划分图如图5所示。

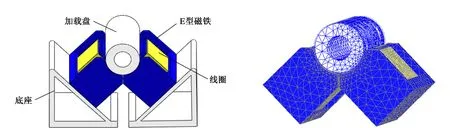
图4 加载装置物理模型图 图5 三维网格划分图

三维瞬态场求解设置：因加载盘处于旋转中，设置停止时间为1 s以及时间步长为0.01 s，在Type选项中选择线性步长(Linear Step)，起始时间为0，停止时间为1 s，步长为0.05 s,并将具体设置添加到时间菜单中，非线性残差设置为0.000 15，进行求解。不同时刻的磁密矢量图如图6所示。

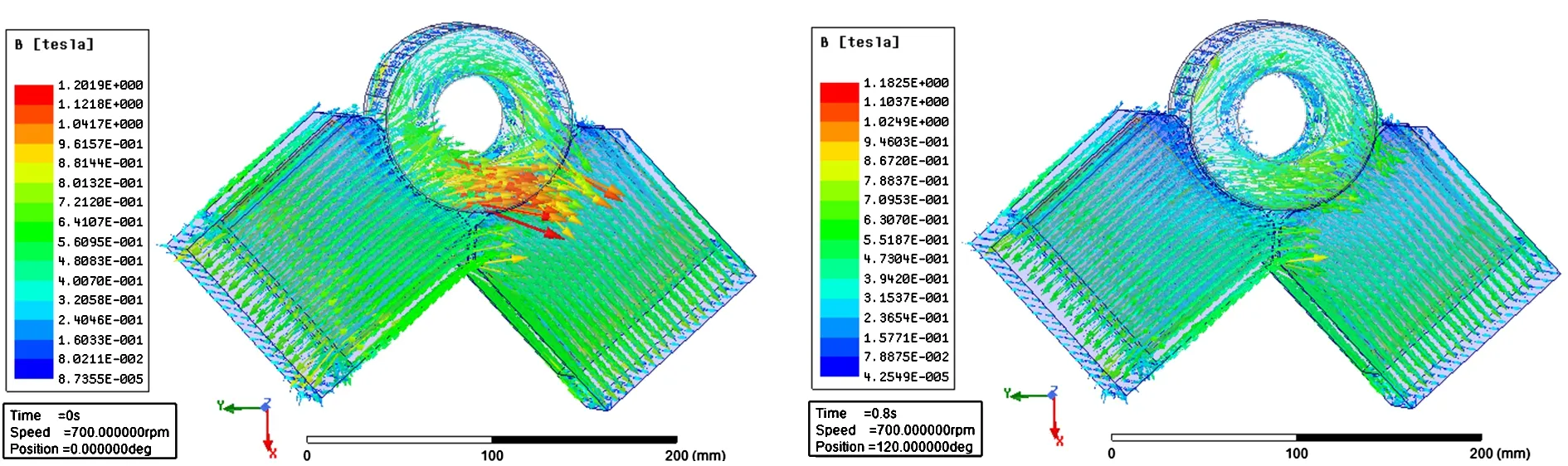
(a)运动初始时刻 (b)运动0.8 s时刻图6 加载装置不同时刻磁通密度矢量图

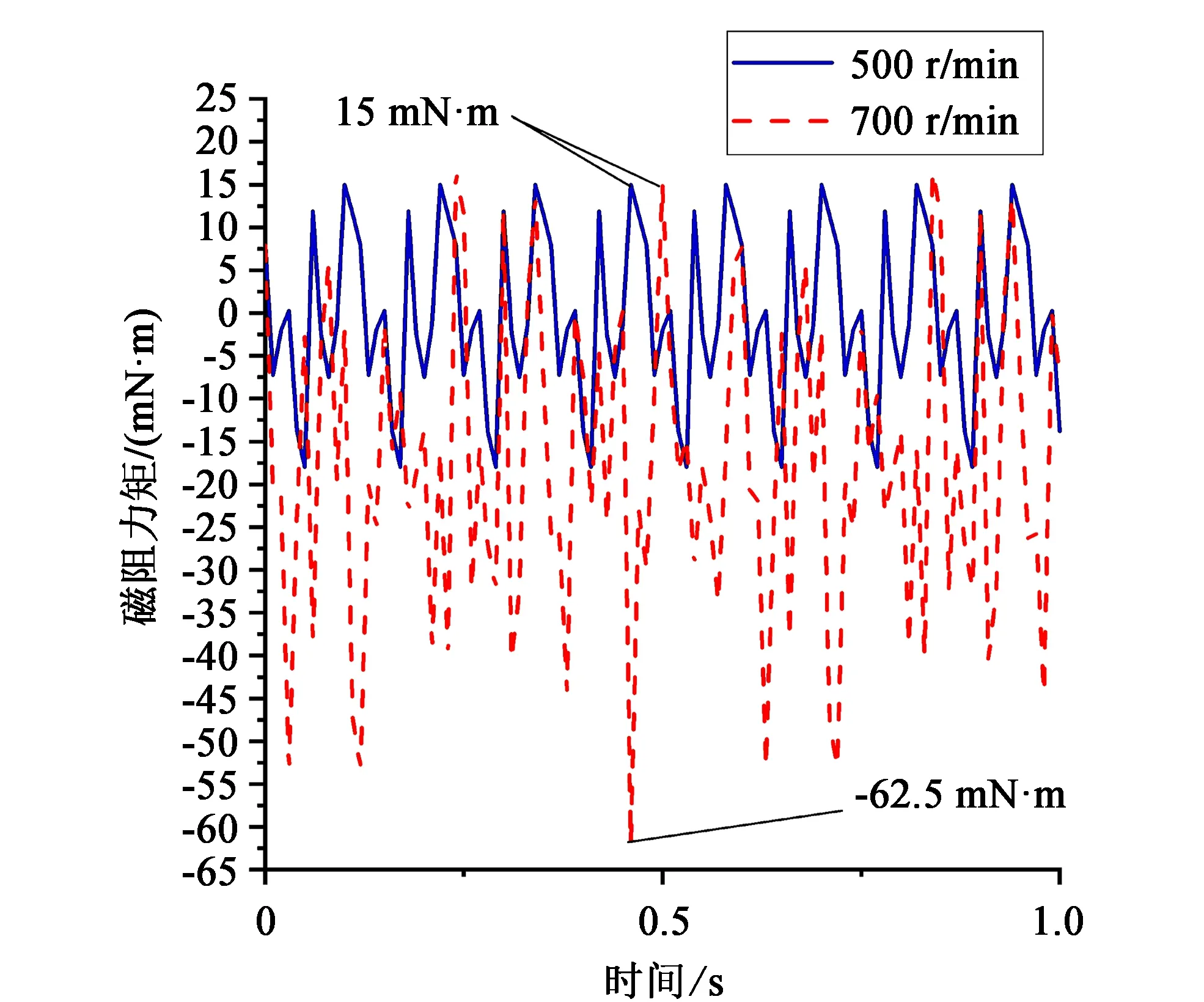
图7 加载装置的磁阻力矩

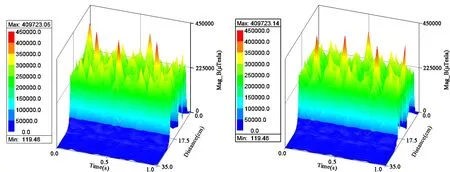
(a)500 r/min (b)700 r/min图8 不同转速下气隙处磁通密度分布

不同转速下，加载装置的磁阻力矩以及加载盘旋转位置如图7所示。轴在旋转过程中，产生磁阻力矩会使轴系转速波动从而产生噪声以及振动。由图7可见，相同时间内，转速越大，磁阻力矩在0范围内波动越大，即轴转速越大，磁阻力矩对轴系的影响越大。图8为瞬态仿真时，加载盘旋转产生的涡流效应对气隙处磁通密度的影响。通过图8可看出，在零时刻，加载盘两侧磁极的磁通密度大致对称，随着转速以及时间的提高，涡流场产生涡流效应，气隙间的磁通密度基本呈现出减弱但也会出现极值，极大值大小随转速升高而升高，且磁通密度不对称，但符合磁通连续定理。

4 理论与仿真结果对比分析

通过将计算数值代入到理论公式，以及在仿真软件中运用场计算器，最后得到理论与仿真电磁力。应用Origin做出理论值与仿真值在给定3种电流激励下的径向电磁力随转速变化曲线，如图9所示。

图9中，加载力随轴转速升高呈非线性减小趋势，这是由于轴转速逐步提高时，集肤效应也逐渐增强，导致加载盘表面磁阻增大，因此，径向加载力逐渐减小。轴转速较低时，加载力变化幅度较大，此时涡流场影响较小，且E型磁铁的磁极对加载盘表面产生的磁未饱和；轴转速较高时，由于涡流场效应增强，E型磁铁磁极处对加载盘表面产生的磁饱和，因此径向加载力变化较小。当激励电流为0.5 A时，理论值与仿真值的最大误差为18.3%；激励电流为1.0 A时，理论值与仿真值的最大误差为18.7%；激励电流为1.5 A时，理论值与仿真值的最大误差为18.0%。总之，理论、仿真电磁力变化曲线趋势一致且径向电磁力随转速升高而减小，随电流升高而增大。因此，在后续试验中可根据理论以及仿真分析结果及时更正加载力大小，使后续研究精确度提高。

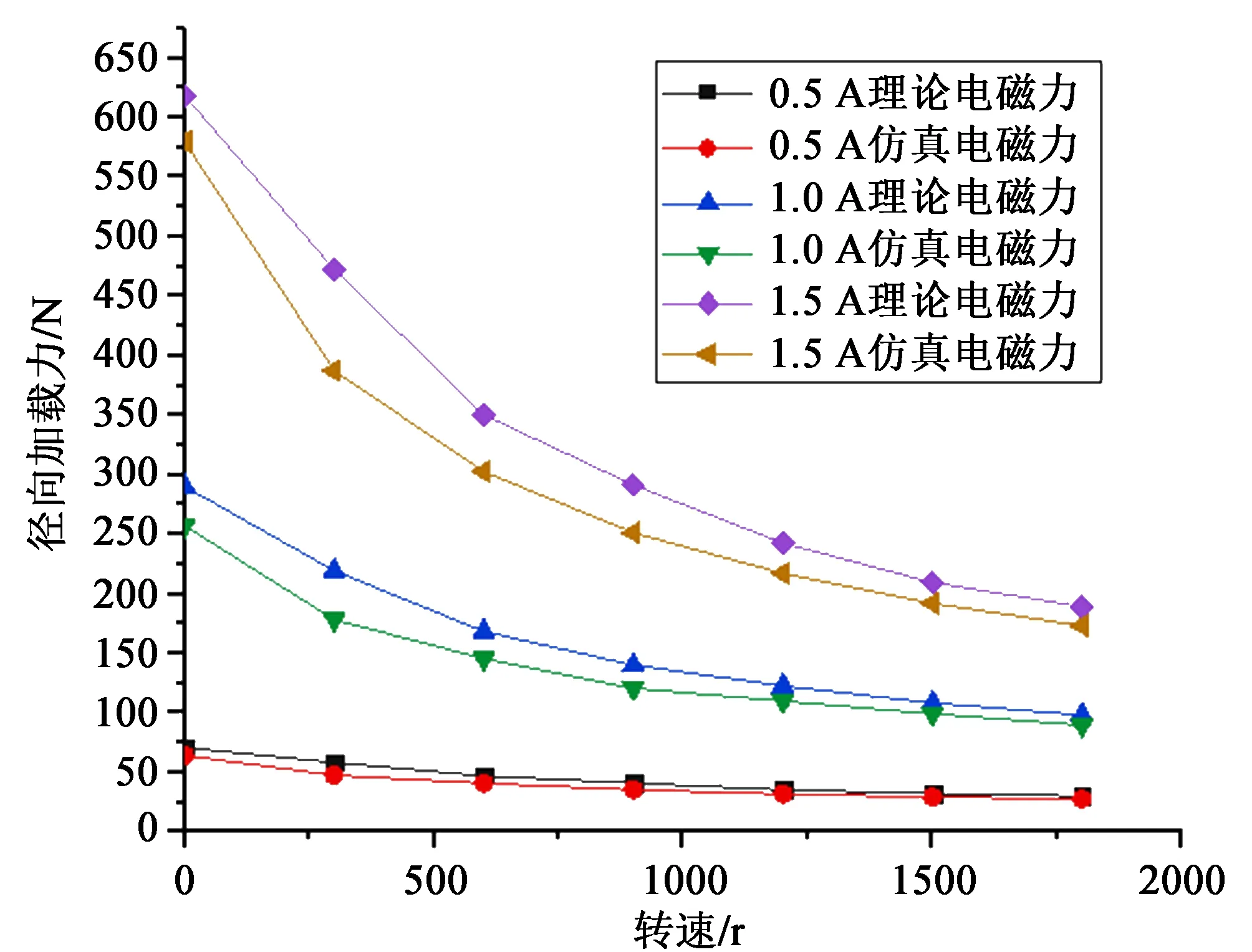
图9 不同转速下的加载力对比曲线

5 结论

(1)磁通密度从E型磁铁端部经过气隙，大部分经过加载盘下半部分并且底部最为密集。随着轴转速的提高，磁阻力矩对轴系影响逐渐增大；零时刻时加载盘两侧磁极的磁通密度大致对称,随着时间增加气隙间的磁通密度基本呈现出减弱但也会出现极值，且磁通密度不对称，但加载盘旋转位置不变。

(2)理论计算、有限元仿真分析均表明，动态条件下的电磁加载装置电磁力与水润滑轴系轴转速有关。在0.5、1.0、1.5 A这3种激励电流作用下，理论值与仿真值的最大误差分别为18.3%、18.7%、18.0%。

(3)后续将设计控制方案，在试验中进一步提高加载力准确性，使得转速变化对加载力影响较小。