基于优化灰色模型的南海鸢乌贼资源丰度预测
2021-06-23周茜涵吴洽儿周艳波谢恩阁马胜伟
周茜涵,吴洽儿,周艳波,谢恩阁,马胜伟
(1.中国水产科学研究院南海水产研究所/农业农村部南海渔业资源开发利用重点实验室,广东 广州 510300;2.西安电子科技大学数学与统计学院,陕西 西安 710100)
鸢乌贼 (Sthenoteuthis oualaniensis) 隶属于枪形目、柔鱼科、鸢乌贼属,广泛分布于印度洋、太平洋的赤道和亚热带海域,其中南海和印度洋西北部海域分布数量较多。巨大的开发潜力与经济价值,使其在我国南海海洋渔业中的地位日益凸显,近年已逐渐成为我国南海重要经济种之一[1]。海洋环境和气候均会对南海鸢乌贼的相对资源丰度产生影响,如海表面温度 (Sea surface temperature, SST)、海平面高度 (Sea surface height, SSH)、海表叶绿素a浓度 (Sea surface chlorophyllaconcentration, Chla)、海表盐度 (Sea surface salinity, SSS)、厄尔尼诺现象[2]、月相等[3],掌握南海鸢乌贼单位捕捞努力量渔获量 (Catch per unit effort, CPUE) 与海洋环境间的变化规律,对准确预测鸢乌贼的资源丰度有重大意义。但由于鸢乌贼资源开发较晚,渔获量统计数据缺少长时间与大范围的积累,且渔民自主填报数据质量较差,传统方法难以对其资源丰度进行准确预测[4]。灰色系统模型由我国邓聚龙教授首创,旨在解决“部分信息已知,部分信息未知”的不确定性系统问题,对时间序列较短的数据和具有不确定因素的复杂系统的预测效果较好[5],近年来已被广泛应用于渔业研究领域[6]。普通GM (1,1) 模型每次仅能观测1个变量,无法体现环境因子的作用;GM (1,N) 模型虽能考虑多个变量的影响作用,体现出多因素共同作用下的趋势预测,但建模精度存在较大偏差,稳定性不足[7]。针对上述问题,许多学者对灰色模型进行了优化改进,如构建无偏模型[8]、优化灰作用量[9]、重构背景值[10]、优化参数估计[11]以及残差序列修正[12]等。本文以2013—2019年春夏季南海鸢乌贼CPUE为资源相对丰度指标,构建鸢乌贼CPUE与环境因子间的灰色预测模型GM (1,N)[13],并对原始预测模型进行优化,以提高预测精度。
1 材料与方法
1.1 数据来源
南海鸢乌贼生产统计资料来自于广西壮族自治区北海市水产推广站渔捞日志,数据包括船名、主机功率、日期、作业水深、经度、纬度、渔区、作业时长、渔获量 (kg) 等,因本文选取的渔船参数变化较小,故暂未考虑渔船参数对CPUE的影响[14]。时间分辨率为天 (d),空间分辨率为经纬度0.5°×0.5°。研究区域为 106°E—120°E、6°N—20°N,时间为2013—2019年。根据鸢乌贼的汛期,本文以每年2—6月汛期为研究对象[15]。
本研究选取SST、SSH、Chl-a、SSS和海表面风速 (Sea surface wind, SSW) 5种与鸢乌贼活动密切相关的环境因子[16],其中SST、SSS、Chl-a和SSW数据来源于美国海洋大气局NOAA气候观测网点https://oceandata.sci.gsfc.nasa.gov/,时间分辨率均为月,SSS和SSW的空间分辨率为0.25°×0.25°,SST和Chl-a的空间分辨率为4 km。SSH数据来源于http://marine.copernicus.eu,时间分辨率为月,空间分辨率为0.083°×0.083°。在ArcGis 10.2中将空间分辨率统一处理为0.5°×0.5°,若存在未记录的环境数据,则采用克里格插值计算得到相应站点的环境数据[17]。
1.2 研究方法
1.2.1 数据预处理 本研究以CPUE作为鸢乌贼资源相对丰度的指标,计算历年各月平均CPUE,计算公式为:

1.2.2 灰色关联分析 灰色关联分析是根据灰色系统中各因素间发展趋势来确定各因素间关联性,对系统的变化趋势作量化度量[19]。本文设序列为2013—2019年各年平均CPUE序列,设序列为历年各月环境因子序列,之间的关联度计算参考余胜威[20]。
各指标对CPUE的影响程度大小与关联度成正比,关联度越大说明影响越大,反之越小。通常关联度大于0.9说明两者之间具有强相关,大于0.8说明两者之间显著相关,大于0.7说明具有相关性[20]。
1.2.3 GM (1,N) 模型预测原理 GM (1,N) 模型是多变量情况下考虑观测点间相关性的动态关联分析模型,能反映系统参数间的影响作用,适用于系统整体分析。设各年平均CPUE序列为,其相关海洋环境因素序列为模型的具体构建计算参考文献[21]。
最终得到G M (1,N) 的响应函数为:

累减还原预测值:
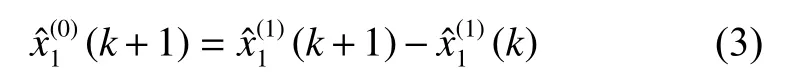
1.2.4 因子重要性分析 因子重要性分析是通过关联度分析和因子组合共同确定因子重要性的方法,即为比较不同环境因子对资源相对丰度预测的效果,模型建立时考虑不同因子的组合模型,拟构建以下6种模型[13]:
模型1:包含所有因子的GM (1,6) 模型;
模型2:不包含SSH的GM (1,5) 模型;
模型3:不包含SST的GM (1,5) 模型;
模型4:不包含SSS的GM (1,5) 模型;
模型5:不包含Chl-a的GM (1,5) 模型;
模型6:不包含SSW的GM (1,5) 模型。
通过相对误差判断模型有效性,即比较以上所有模型的相对误差大小来间接说明该环境因子的重要性[22]。
1.2.5 基于Simpson公式的背景值优化 GM(1,N) 模型的预测值依赖于原始数据序列及其背景值,因此背景值的合理构造将对提高模型预测精度起重要作用。通常使用的两点间中值误差较大,且会造成预测值数据不够平稳,故此选用Simpson公式对背景值进行改造[21]。
新的背景值写作[23]:
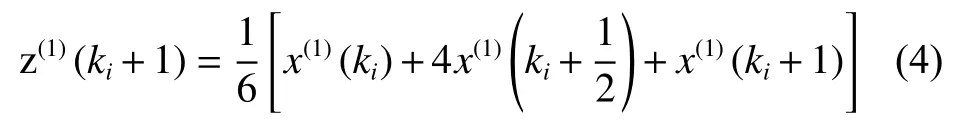
1.2.6 基于Fourier级数的残差修正 灰色GM(1,N) 模型在进行中长期预测时预测精度会衰减,针对这个问题,可以基于构建残差的GM (1,1) 模型[24]、Markov链[25]、自适应滤波法[26]等方法修正。本文采用Fourier级数对预测误差做拟合修正。定义灰色GM (1,N) 模型的残差序列为:
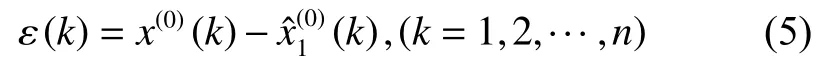
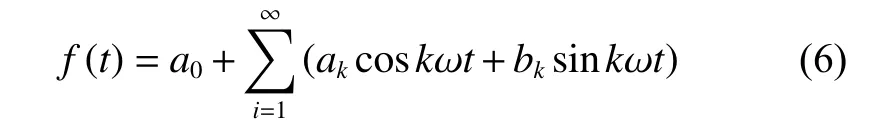
其中模型相应参数可通过Matlab 2017a软件求解[27]。
2 结果
2.1 CPUE年际变化规律
南海鸢乌贼年CPUE存在较大的变动,2013—2015年逐年增加,在2015年达到最高值(2.66 t·d−1)后下降至 2016 年的 1.93 t·d−1,随后在 2017—2019年间呈稳步增长的趋势 (图1)。
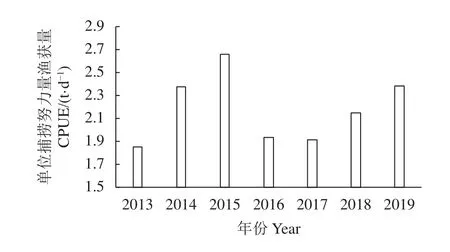
图1 2013—2019年南海鸢乌贼单位捕捞努力量渔获量变化Figure 1 CPUE of S.oualaniensis in South China Sea from 2013 to 2019
2.2 灰色关联分析
环境因子中Chl-a、SST和SSW的关联度皆大于0.8,属于显著相关;SSS和SSH的关联度大于0.7,具有相关性 (表1)。其中影响最大的因子是Chl-a,其灰色关联度平均值为0.953 5;其次为SST,平均关联度为0.848 0;第三为SSW,平均关联度为0.833 8。
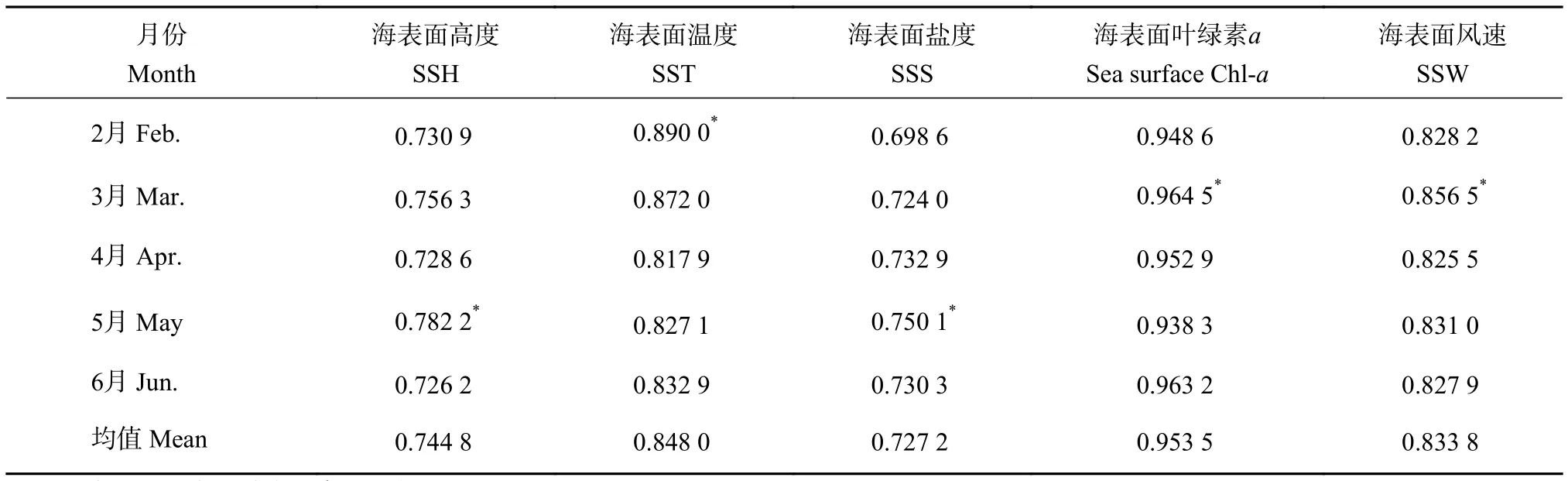
表1 环境因子序列与单位捕捞努力量渔获量的灰色关联度分析结果Table 1 Grey relational analysis of environmental factor sequence and CPUE
从月份因素分析,3月的Chl-a和SSW、2月的SST、5月的SSH和SSS分别为各因子中关联系数最大的月份,因此在之后GM (1,N) 模型构建中,采用上述5项因子作为南海鸢乌贼资源GM(1,N) 模型建模的备选因子。
GAM模型分析表明 (图2),鸢乌贼CPUE集中分布在 Chl-a质量浓度介于 0.07~0.19 mg·m−3的区域,最适宜 Chl-a质量浓度为 0.09~0.13 mg·m−3;鸢乌贼CPUE集中分布的SST介于24~31 ℃,最适宜SST为27~29 ℃;鸢乌贼CPUE集中分布的SSW介于 2.0~10.0 m·s−1,最适宜风速为 4.5~7.0 m·s−1。
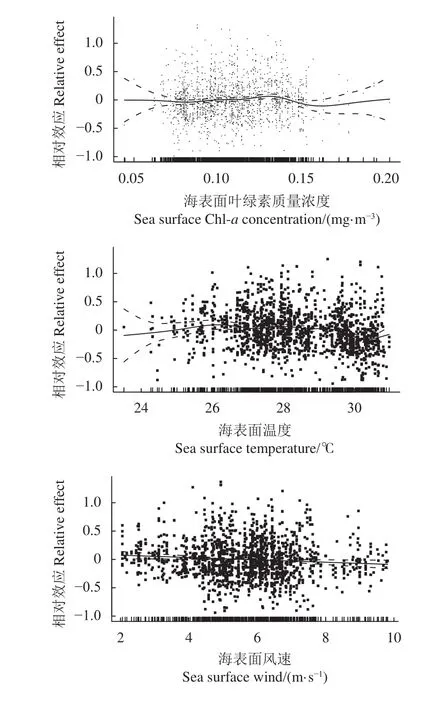
图2 海表面叶绿素质量浓度、海表面温度和海表面风速对单位捕捞努力量渔获量的影响Figure 2 Effects of sea surface Chl-a concentration, sea surface temperature, sea surface wind speed on CPUE
2.3 灰色预测模型
选定指标后,用2013—2018年CPUE和环境因子数据建立灰色预测模型,多种因子组合模型的平均相对误差见表2。从平均相对误差上看,模型M6 (不包含SSS) 和模型M3 (不包含SSW) 相对误差值较大,模型M1 (包含全部因子) 相对误差最小,即模型M1为最优预测模型,能够较好地模拟南海春、夏季鸢乌贼的资源丰度。

表2 多因素预测模型得到的单位捕捞努力量渔获量拟合值与真实值的相对误差Table 2 Relative error between CPUE predictive value and real value obtained by multi-factor prediction model
2.4 优化的 GM (1,N) 模型
表3为CPUE真实值与普通GM (1,6) 模型、基于Simpson优化的GM (1,6) 模型和基于Fourier级数修正的GM (1,6) 模型3种模型拟合结果的比较。因数据列较短,在此只选用2019年的数据作验证。

表3 3种模型的拟合结果与单位捕捞努力量渔获量真实值的相对误差Table 3 Relative error between predictive values of three models and real CPUE value
普通GM (1,6) 模型平均相对误差为7.78%,预测的2019年CPUE误差为4.79%。
根据公式 (4) 计算基于Simpson公式的GM(1,N) 模型,平均相对误差为7.69%,预测的2019年CPUE误差为3.46%。
根据公式 (6) 使用2013—2018年残差拟合Fourier级数得到级数表达式为:

模型残差平方和SSE=0.025,拟合优度值R2=0.879,均方根误差RMSE=0.158 2,此时基于Fourier级数修正的GM (1,N) 模型的平均相对误差仅为2.62%,预测的2019年CPUE相对误差仅为1.87%。
普通GM (1,6) 模型的结果不平稳,在2014和2017年的拟合上出现了较大的误差;基于Simpson优化的GM (1,N) 模型预测数据平稳但仍有误差;而基于Fourier级数残差修正的灰色GM (1,N) 模型基本能拟合真实值 (图3)。
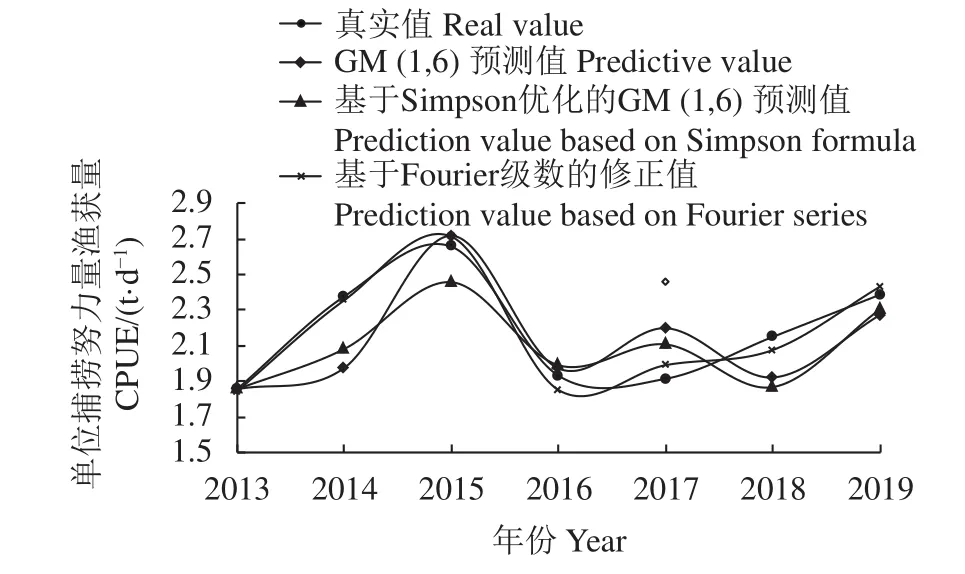
图3 3种模型的拟合结果与单位捕捞努力量渔获量真实值的比较Figure 3 Comparison between fitting results of three models and real CPUE value
3 讨论
本研究以CPUE为指标,结合海洋环境因子,采用灰色系统理论预测春夏季南海鸢乌贼的资源丰度,并用数值积分中的Simpson公式和Fourier级数对模型的背景值和残差进行修正,得到较普通灰色模型精确度更高的预测方法。
3.1 环境因子对CPUE的影响
灰色关联度结果表明,Chl-a对鸢乌贼CPUE的影响最大,其灰色关联度平均值为0.953 5。在渔场的变化中,Chl-a浓度决定了海域生产力高低以及摄食环境优劣,而摄食环境是决定鸢乌贼补充量的重要因素[13]。本研究结果显示,鸢乌贼集中分布在 Chl-a质量浓度介于 0.07~0.19 mg·m−3的区域,最适宜 Chl-a质量浓度为 0.09~0.13 mg·m−3。这与余景等[16]报道的中西沙鸢乌贼最适Chl-a质量浓度为 0.10~0.13 mg·m−3的结果一致。
鸢乌贼的生存环境与温度密切相关[14]。徐红云等[28]报道南海鸢乌贼中心渔场最适宜SST为26.4~29.6 ℃;晏磊等[29]研究认为不同季节鸢乌贼对温度的适宜性范围也有所变化,春季最适SST为25.6~29.6 ℃,秋季为27.6~30 ℃。本研究中SST对CPUE的影响仅次于Chl-a,关联度为0.848,主要分布在27~29 ℃,与上述研究结果基本一致。
SSW的平均关联度为0.833 8。本研究中鸢乌贼 CPUE分布在 SSW 介于 2.0~10.0 m·s−1的区域,其中最适宜SSW为4.5~7.0 m·s−1。风速对鸢乌贼CPUE的影响与灯光罩网作业的特点有关,大风天气会严重影响罩网渔船捕捞作业,在海上风速较大时其捕捞活动较少。
此外,有研究表明,SSH也是影响鸢乌贼资源丰度的一个重要因子,SSH高于平均海面有利于海水的辐散上升,带来丰富的营养物质,使浮游生物大量繁殖,充足的饵料可促进中上层鱼类的生长、繁殖[30]。但本研究将整个海域SSH进行了平均,且研究时间仅2—6月,弱化了SSH对CPUE的影响[13]。
3.2 优化灰色模型的作用
灰色GM (1,N) 模型结果显示,包含所有因子的模型M1对鸢乌贼资源丰度有较好的预测效果,能较准确地反映CPUE的变化趋势。灰色系统模型突破小样本数据的局限,对时间序列较短的数据也有良好的预测效果,对数据缺乏的渔业科学具有重要意义。
针对普通灰色模型预测误差较大的问题,本文首先使用Newton-Cotes公式改造背景值,用Simpson公式代替梯形公式,降低背景值带来的误差。将GM (1,N) 模型的平均相对误差由7.78%降至7.69%,使预测数据序列更平稳;且与普通GM(1,N) 模型相比,使2019年CPUE的预测误差从4.79%降至3.46%,因此改造背景值对于优化预测结果有一定意义。此外,用Fourier级数对GM(1,N) 模型的残差作拟合,利用其良好的数据逼近能力对预测误差进行修正,将数据序列的平均相对误差由7.78%降至2.54%,将2019年CPUE的预测误差从4.79%降至1.87%,说明Fourier级数修正能够有效地提高模型精度,减少相对误差,使结论更具实际价值。
综上所述,本研究通过灰色关联分析法构建鸢乌贼CPUE与环境因子间的关联度,选取合适因子构建灰色预测模型对南海鸢乌贼资源CPUE进行预测,并对其结果进行修正,使优化后的模型较之前的精度有明显提高,这对更准确预测鸢乌贼资源丰度提出了一种新思路。但本文未考虑因子交互项对南海鸢乌贼CPUE的作用,加上灰色系统模型本身的局限性,如快速衰减和递增的属性,使长期预测结果的准确性较低。本研究因GM (1,N) 模型对加入的影响因素的限制,在计算CPUE时采取了平均的算法,降低了样本量。因此,今后可尝试其他预测模型,如神经网络模型[31]和回归树模型[32],两者均具有良好的非线性映射能力和学习能力,在大样本量条件下能获得更高的预测结果;此外,支持向量机模型[33]能根据有限的样本信息在模型的复杂性和学习性之间寻求最佳解,在小样本情况下得出较好的预测结果,从而获得更加准确的南海鸢乌贼CPUE预测模型。
