博弈搜索树算法的实现及其优化

周子龙

（同济大学 软件学院，上海201804）

1 概述

在一般的搜索过程中，总是会有一个限定的、有限的搜索内容集。一般的搜索算法也仅仅限于在该固定集中进行查找操作，返回是否查找成功，即待查找的元素是否属于该集合。而在许多情境中，该类搜索并不能满足用户的全部需要，有时候，我们并不是搜索某一特定的元素，而是给出集合中最符合用户需求的元素。这些元素并不是绝对确定的，当一定是在某一些特定要求下，根据某种评估，所能在有限的搜索集合中给出最有元素；同时，搜索的集合可能在需要执行搜索的时候还未产生，需要一边搜索一边动态的产生新的元素。一般地，我们把符合上述描述的搜索称为动态博弈搜索。相较于普通搜索，博弈搜索的搜索集合并不是可以立即确定的，它可能需要根据不同局中人的不同行为生成不同元素进行不断补充；以及，该过程也涉及到多个参与者，即上文提到的多个局中人，每一局中人均假设为理性博弈者，即其所作出的任何行为均是符合一定标准下利益最大化原则。综上，动态博弈搜索树是一种对动态决策的过程模拟，它在搜索的过程中同时产生许多新的可能的结果，依据利益最大化原则，为每一为局中人进行操作，搜索出来的最优行为即应当满足如下要求：通过该最优行为，当所有局中人按照自己利益最大化原则进行后续行为后，该行为为己方带来最大收益。

在理想情况下，总是认为考虑到的情况越多越好，但计算机的算力总是有限的，在现实生活中，局中人的思考能力以及思考时间也是有限的，故搜索不能无限制的进行下去，只可能在有限的搜索深度下，得到当前局面的最优行为。此外，不可否认的是，以往的经验也会影响到局中人的决策。局中人总是会依据一定的经验进行判断，而不是每遇到一个局面就从新开始进行判断。据此，在算法中，我们可以考虑加入历史数据库，在每一次搜索做出判断时，先行搜索历史数据，一起到一定的启发作用。至此，我们的目标便已经明确：在一定的规则下，为一个指定的局中人产生根据特定判断下，特定行为局数后，能够对该局中人最优利的行为。后文中，主要分析了如下的几种搜索算法：极大极小值搜索算法、负极大值搜索算法、Alpha-Beta 剪枝算法、结合Hash 表的Alpha-Beta 剪枝算法等。

2 算法及其优化

2.1 极大极小搜索算法

2.1.1 基本思想

根据理性博弈人的基本假设，为了简化搜索逻辑，我们可以做出这样的简化：己方局中人在进行判断时，总是为自己选择利益最大的行为，在模拟其它局中人判断时，总是选择使得己方局中人利益最小的行为。此时，整个的博弈过程为：轮到己方局中人行为时，进行搜索，在当前局面下所有可能的行为中选择对己方局中人利益最大的一种行为。但在实际情况中，一次考虑总是远远不够，在前文也提到了搜索深度的概念，故我们应当认为，也应该为其它局中人进行模拟行为，并以此为己方局中人优化决策。按照如上假设及搜索的基本思想，便是极大极小搜索，其基本思想如下：在每一次迭代中，为每一个局面生产所有可能的子局面，通过极大极小的原则，为不同的局中人选择行为，在向上回溯的过程中，通过子局面的评估，给出父局面的评价。继续向上回溯, 依次类推, 一直到当前局面, 最终相对的最优行为也就搜索出来了。如图1 中：第一阶段轮到蓝方行为，蓝方将选择所有局面评估中对蓝方最有利的一种(57)，之后蓝方将模拟红方行为，并选择对蓝方评估最小的行为(19)。

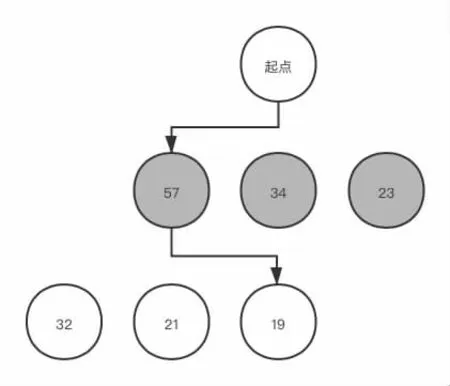
图1

对这种极大极小过程的模拟，即是极大极小搜索算法。根据这种思想，Shannon 最先于1950 年提出该算法，从而奠定了整个博弈搜索的理论基础。但在整个极大极小的过程，我们需要为不同的局中人执行不同的操作，为己方取极大值，为另一方取极小值，为了消除这两方面的差别，Kunth(1975)提出的负极大值算法通过将父节点的评估值设定为所有子节点的负数的极大值，从而达到为双方取相同的操作，使得算法更加简洁，但由于其原理于极大极小搜索算法完全等效，故本文不再给出其具体实现。

2.1.2 性能分析

在某一深度D 下，所有可能的行为数N 对于任何局中人来说应当认为是相近的。每一次生成所有走法涉及到N 次操作，对于每一次评估操作，不妨设其时间复杂度为o(E)，执行和撤销所有行为可以认为其时间复杂度为o(ND)，则该算法具体的时间复杂度为o(END)。

在每一局面中，均为所有可能的行为生成了相应行为栈进行存贮，栈的大小大致于所有可能的行为数相当，则空间复杂度应为o(ND)。不难看出，该算法的执行时间复杂度以及空间复杂度均随着搜索深度指数增长，在具体的博弈过程中是亟待优化的。

2.2 Alpha-Beta 搜索算法

2.2.1 基本思想

针对极大极小搜索算法巨大的时间空间消耗，进一步分析其搜索过程，不难发现有许多搜索是无用的。其中存在着两种明显的冗余计算。第一种是极大值冗余现象。考虑这样一种情况：假定在某一次搜索中父节点A 的评估值为子节点B、C 中的较大者。现子节点B 已经全部搜索完毕，程序开始搜索子节点C。根据极大极小原理，子节点C 的评估值应为其全部子节点中的最小值，在搜索C 的子节点C1 时，已经得到C1 的评估值小于B 节点的评估值，那么，对于C 节点余下的子节点便失去了搜索的必要。这是因为C 节点是选择其子节点最小值，并最小值不会大于C1 的值，故C 节点的值不会大于C1，又因C1 小于B，因而得出B 必定大于C，所以C 节点的估值在此时便可以判定不会影响父节点A 的评估。故而C 节点接下来的搜索便是多余的。

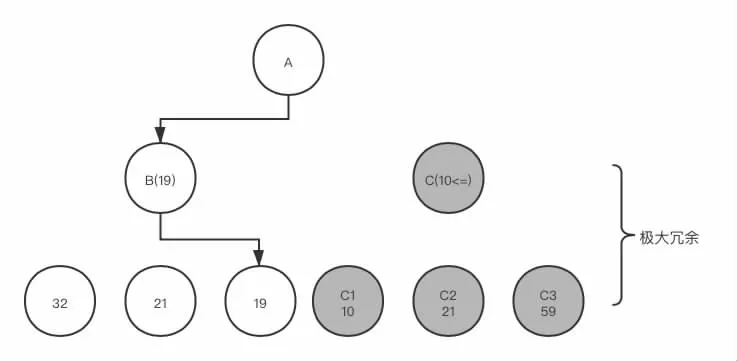
图2

类似的，第二种情况便是极小值冗余现象。现在考虑相反的情况：当父节点A 要取子节点中最小值，此时子节点B 已经搜索完毕得到估值，程序开始继续搜索子节点C，而C 节点应为其子节点中的最大值，这时，倘若C 的某一个子节点C1 的估值大于B 节点，类似的，可以得出C 节点的余下子节点的估值便对父节点A 的评估没有任何贡献。

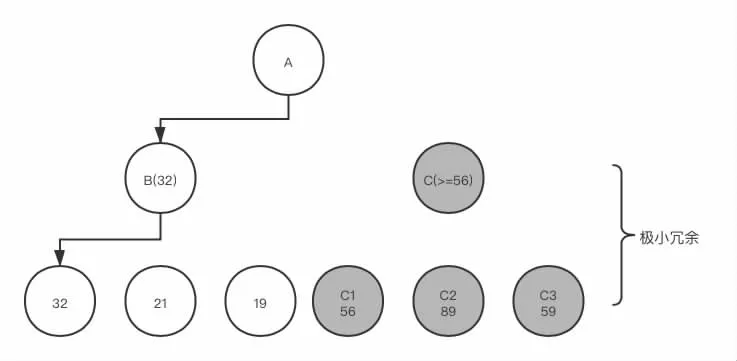
图3

我们称第一种冗余为极大冗余，对应的，当发现产生这种情况时便对这些多余的搜索分支进行修剪，称为Alpha 剪枝。对第二种优化称为Beta 剪枝。将这两种优化方案运用到极大极小搜索算法中便构成了Alpha-Beta 搜索算法。其具体的实现为：在每一次搜索过程中，记录搜索极大值的节点的当前最优值为α,搜索极小值的节点的当前最值为β。在每一次搜索开始时，将α,β 分别设置为机器最小值和机器最大值。这样，在搜索的过程中间便能使得α,β 构成一个窗口，从而跳过没有落在这个窗口的子节点的搜索分支，达到减少搜索次数的优化目的。

其总的行为流程图如下：

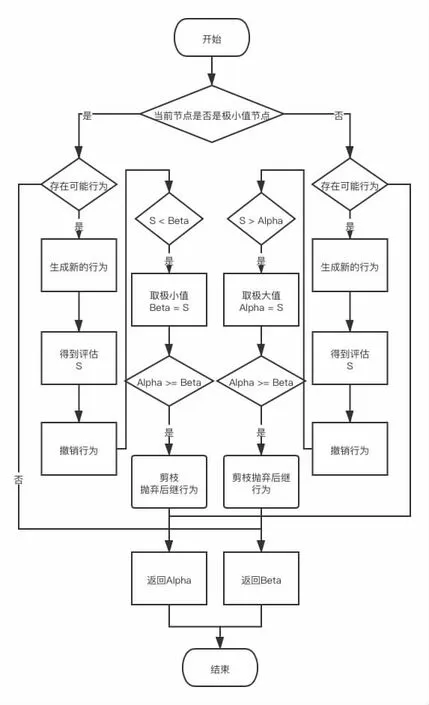
图4

2.2.2 Alpha-Beta 性能分析

根据Kunth 等人的证明，在子节点排列最理想的情况下，即搜索到的第一个子节点估值就不落在[α,β] 窗口内内，使用Aplha-Beta 搜索D 层生成的节点数目N 为

ND= 2bD/2-1 ( D 为偶数)

ND= b(D+1)/2+b(D-1)/2-1 ( D 为奇数)

这样，时间复杂度降到了约极大极小搜索算法1/2 倍，为o(END/2)。

2.3 对上述搜索策略的优化

通过Alpha-Beta 剪枝过后，我们极大的优化了搜索次数，但从Kunth 等人的假设也不难看出，真正优化程度于节点的排列序列高度相关。由于Alpha-Beta 剪枝对中体的子节点排序，即当前局面的下一步的行为高度相关，那么，如果能够粗略的对当前局面产生的所有可能的行为有一个判断，以便能更快地缩小[α,β]的范围，从而产生更多的剪枝。这就涉及到了关于行为排序的思想。其次，在之前的多次索索中，难免会出现许多重复估值的现象，即可能通过不同的行为顺序达到同一局面，这也会造成时间上的浪费，故可在搜索是建立历史数据库，以期之后遇到重复局面时能够减小评估开销，从而降低时间复杂度。这便是结合历史经验进行判断的思想。

2.3.1 行为排序

为了进行行为排序，我们需要对当前局面进行大致判断，将当前局面看似最无意义的行为放在搜索的后面，将可能产生最优解的行为放在前面进行搜索。这便十分依赖于博弈者所面临的具体博弈的条件，下面仅仅以中国象棋为例，简要阐明该思想。岳金朋(2008)在讨论针对中国象棋的优化中提出了一种静态评价的启发，他将行为分为了吃子行为和非吃子行为。在吃子行为中，通过简单的对被吃子是否有其它棋子保护，而导致吃子后我方棋子可能被吃来对每一吃子行为进行排序。简而言之，他将被吃子的分数减去我方行为完后可能被吃子的分数作为判断依据进行排序。对与非吃子行为，岳金朋提出可以首先生成车的行为，最后生成帅的行为，在生成车的行为中，先考虑向前走的行为，后考虑向后走的行为，也可以起到一定的排序选择作用。

2.3.2 历史启发

由于历史启发策略需要用到历史数据库，对每一个历史局面进行保存。Zobrist(1970)提出了一种根据目前局面的所应方法，经过验证，该方法在搜索局面时十分高效。Zobrist 的具体方法是，对于每一个局面而言，其唯一的标示就是当前所有状态的异或值。同时，Zobrist 提出，在所有的博弈搜索算法中，层次更深的搜索往往意味着更加稳健的评估，故对于每一个历史局面的保存应该考虑到该局面的搜索深度。进而结合上文提到的行为排序的思想，我们也应当考虑某一局面能够引发的剪枝数量，一般而言，如果在同一层次的搜索中，如果能够将能够引发剪枝数量更多的行为先行搜索，也可以极大的优化算法的时间复杂度，因此，我们也应该保存某一行为所能引发的剪枝数量。在Zobrist 的局面表示方法下，我们以此生成Hash 表进行存储每一个局面的具体信息。具体的Hash 表的实现原理于此不过多赘述，参见参考文献[6]。具体而言，假设现在要对某一局面进行d 层搜索，当前窗口是[α,β]，而通过上述方法发现历史中该局面已经存在，评价为v，类型为t，经过了d’层搜索。如果t 为精确型估值，即在历史中的搜索该局面没有因为剪枝而放弃搜索，便可以直接返回v 而代替索索。如果t 为模糊型，则判定是否高过边界，从而判断是否可以直接引发剪枝。

2.4 浅层搜索优化策略

与Shell 对插入排序算法的优化类似，Krof(1985)也提出了对Alpha-Beta 搜索算法的一种可能的优化方案。Krof 的基本思想是，在生成走法时，先进行较为初级的浅层搜索，在上文中对Alpha-Beta 搜索算法的性能分析中我们不难看出，搜索复杂度伴随着搜索层次成指数级增加。对于一个D 层的搜索而言，（D-2）层的搜索的复杂度完全与其不在一个数量级上。倘若在搜索生成走法前，先通过一个d 层的浅层搜索来对所有行为进行排序，那么，那些在浅层搜索中的较优行为就将在深层搜索中较前被尝试，从而得到更高的剪枝效率。

2.5 本文提出的优化方案——伪搜索策略

上述的诸多改进全部是基于既定时间内尽可能搜索多的深度，以深度提高程序的智能程度。然而，上述改进全部是基于搜索前的改进，这可以极大的减少搜索量级，以换取更多的搜索时间。不过，本文在实际中发现，在同一搜索量集中，不同搜索次数并不会很大的影响搜索时间，如共执行N 次搜索和执行2N 次搜索时间开销并不大。但后者无疑进行了更多次的搜索，在表现上理应更加高效。因此，倘若在所有搜索结束，再进行一些浅层的判断，对程序的表现无疑是有益处的。设初始量级为N，每层生成M 个行为，共搜索D 层，则有：N=MD。若对第D 层行为进行复杂度为P 的浅层判断，则总共的量级N'应有：

N'=N+M×P

其中：M×P＜＜N

故对总的程序无显著影响，而判断次数更高，可以获得更好的表现。

3 测试

至此，我们完成了对整个博弈搜索过程的优化。由于本文并不针对任何一种博弈过程，只是提出针对博弈搜索过程的算法及其优化，无法进行具体的性能分析，下文将以中国象棋为例，讨论优化的具体效果。在基于挑夹棋游戏规则进行以类似本文2.2 的Alpha-Beta 搜索和通过2.3.1 行为排序进行优化后的算法进行比较，得到如下结果：

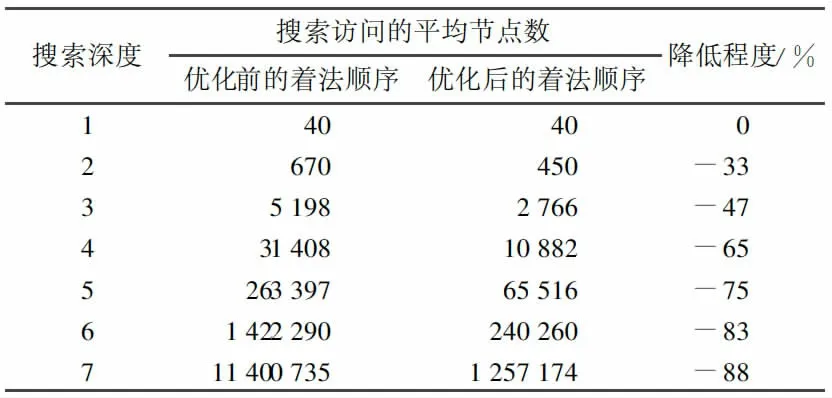
表1

通过2.4 浅层搜索优化，与普通的Alpha-Beta 搜索进行比较，得到如下结果：

表2