基于GIS的江西省气温空间插值方法比较

徐谢亲，祝明霞

(九江学院 旅游与地理学院，江西 九江 332005)

1 引言

近年来高温，洪涝灾害等极端事件频发，为了更好地解决影响人们已久的气候问题，不仅要掌握气象要素的变化规律，还应能够做到预测气候的发展趋势。这就需要借助实测站点提供真实可靠的观测数据，以便有关人员进行相关研究分析。但是在实际生活中，由于人力，物力等各方面的限制原因，我国气象站点在密度上远远不够，又因为地理位置的差异，空间分布也较为不均匀[1]，尤其是在地形复杂多变的偏远山区[2]，有些省份即使气象站点数量相对较多，但是仍然难以满足全区域覆盖的要求。为解决这一问题，需要对数量不足且分布不均的气象站点的实测数据进行插值运算，以便得到整个研究地区的气象数据。通过研究比较常用的空间插值算法，从中找出对江西地区的气温研究效果理想的空间插值方法。由于各地区的气象站点分布情况不一，地形条件、自然环境有所差异，因此对于不同的空间插值技术，需要用不同的栅格化方法进行研究[3～6]。选取张力样条函数法(Tension Spline)、反距离权重法(IDW)以及普通克里金法(OK)对江西省年平均气温进行空间插值，并进行精度验证比较。

2 研究基础

2.1 研究区概况

江西省位于中国东南部，处于24°29′～30°04′N至113°34′～118°28′E之间。主要地貌类型是山地和丘陵，平地较少，北部的地势相对比较平坦，东西南部三面被山脉所包围，中部丘陵高低起伏。全省气候温暖，四季分明，雨水充沛，亚热带湿润气候，十分适合农作物的生长。全省森林资源保护良好，森林覆盖率位居全国前列。江西是一个重要的农业省份，降水量、气温等的变化对于江西地区农作物生长具有重要影响，因此研究江西地区气温的空间分布有着十分重要的意义。

2.2 数据来源与处理

主要数据为江西省气象站点的历史数据，包含站点的经度、纬度、海拔高程、年平均气温等，时间跨度为1981～2010年。数据来源于中国气象数据网(http://data.cma.cn)。

首先将经纬度数据在Excel表格中进行单位转换，再汇总整理，后导入ArcGIS10.2，使用的地理坐标系为GCS_WGS_1984。剔除不连续、冗余等数据，确保气温数据的准确性[7]，最终选取研究区内83个站点以及邻近省份49个站点的30年年平均气温数据参与插值运算，并且均匀选取江西境内20个气象站点作为检验点，其余的112个气象站点作为插值点。在软件ArcGIS10.2中，加载江西省DEM，插值点和检验点，得到江西省内外气象站点的空间分布图(图1)。

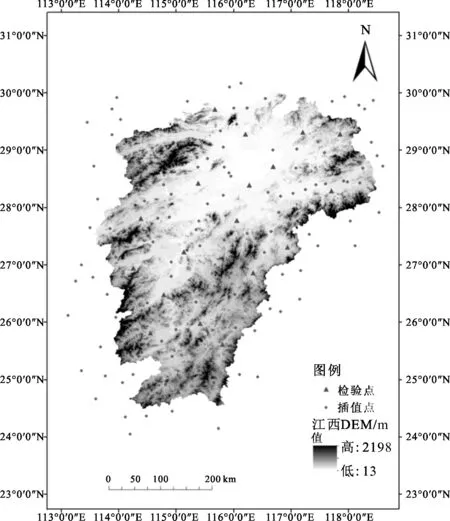
图1 江西省及其邻近省份气象站点分布

2.3 空间插值方法与验证

2.3.1 空间插值方法

反距离权重法，简称IDW，其原理是相似相近[8]，即已知点与插值点之间的距离越近，则已知点对插值点的影响就越大。反距离权重法容易受极值点的影响，产生“牛眼”现象，适合气象站点数量较多且分布较为均匀的地方。

张力样条函数法能够根据建模现象的特征调整插值的硬度，插值的结果更接近样本点范围，适用于温度的研究，张力样条函数法能够反映出局部的特征，但是在气象站点稀疏时插值效果不好。

普通克里金法，简称OK，属于克里金法的一种，是最早被广泛提出和进行系统研究的克里金法[9]，亦被称之为局部估计或是空间局部插值法，并且伴随着当今世界各国的统计学技术的进步而衍生和发展出一系列的变体和改进算法。普通克里金法适用于空间自相关程度较高的数据，能够对已知的采样点误差做出理论上的估计。

2.3.2 插值结果验证

为了比较上述几种插值方法的插值效果，对江西省气温数据进行空间插值之后，采用实际验证法进行精度比较。通过阅读大量相关文献，参考前人研究方法，选用平均绝对误差(MAE)、平均相对误差(MRE)和均方根误差(RMSE)进行插值精度研究比较。由于插值点与检验点的比例过大或过小都将对验证结果产生较大影响，导致验证结果不够准确，参考前人研究文献，最终选取15%(20)的气象站点作为检验点，其余的气象站点(112)为插值点。MAE和MRE能够定性地反映出误差的范围，插值结果比较直观[10]，RMSE同样是衡量插值精准度的方法之一[11]。它们的计算公式被定义为：

(1)

(2)

(3)

式(1)～(3)中，n表示检验站点的数目；Oi表示实测值；Pi表示预测值。MAE、MRE、RMSE的值越小，表明拟合度越好，即插值效果越好。

3 不同空间插值结果分析与评价

3.1 不同空间插值结果分析

运用2.2和2.3部分的方法，得到江西省近30年来年平均气温插值结果(图2)。实现过程如下：打开软件ArcGIS10.2，找到ArcToolbox工具箱，使用Spatial Analyst工具中的插值分析功能，选择相应的插值方法，输入插值点点要素，Z值字段设置为“累年平均气温”，得到江西省及其周边的预测气温栅格图，最后根据江西省DEM的轮廓掩膜提取出基于空间插值方法的江西省预测气温栅格图。

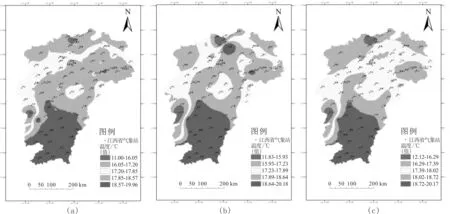
图2 江西省年平均气温插值

由图2可知，使用这三种插值方法，得到的江西省年平均气温分布范围相差并不大，说明，江西省的气温空间自相关程度较高，省内气象站点的分布较为理想，能够满足插值研究。

使用反距离权重法(图2a)得到的年平均气温的范围为11.93～19.96 ℃。其中，赣州大部分地区，如兴国、于都、安远、信丰等地年平均气温普遍较高，庐山和井冈山地区气温最低。利用反距离权重法插值得到的预测值与实测值的MAE为0.3505，MRE为1.9538，RMSE为0.4355，整体上误差较小，IDW的插值效果较好。

使用张力样条函数法(图2b)得到的年平均气温的范围为11.83～20.18 ℃。总体上看，样条函数法生成的拟合表面连续光滑，但是也容易产生过于理想化的偏差，导致误差增大。由图可知，都昌地区在插值图中属于18.64～20.18 ℃的温度范围，这与实际情况不符，根据气象站点实测值，都昌地区的年平均气温为17.4 ℃。张力样条函数法插值结果与预留站点实测值MAE为0.53，MRE为2.9704，RMSE为0.8441，整体误差比反距离权重大，插值效果不如反距离权重法。

使用普通克里金法(图2c)得到的年平均气温的范围为12.12～20.17 ℃。普通克里金法的插值结果与气象站点实测值的MAE为0.366，MRE为2.0394，RMSE为0.4675，插值效果介于IDW和Tension Spline之间。

反距离权重法、张力样条函数法和普通克里金法都能够大致地预测江西省的气温，反映出省内气温的变化趋势。从总体上看，三种空间插值方法得到的江西省年平均气温在空间上具有一致性，年平均气温呈现出南高北低的趋势，气温变化具有明显的纬度地带性，但是随经度的变化表现不明显。其中，庐山和井冈山的气温居于全省最低，这与气象站点的海拔高度有关，通常情况下海拔升高时温度会降低，庐山气象观测站的海拔高度为1164.5 m，井冈山为843 m，为江西省内海拔高度最高的两个气象站，使得庐山和井冈山的年平均气温低于周围其他地区。

3.2 不同空间插值结果比较

基于3.1得到的不同插值方法的江西省预测气温栅格图，采用GIS中的提取分析功能，提取出检验点的预测气温值。表1为20个预留检验气象站点的实测值与不同空间插值方法得到的预测值的比较。

表1 预留站点实测值与插值结果对比分析 ℃

由表1不难发现，使用反距离权重插值法，所有检验站点的插值结果与实测值误差均小于1 ℃，其中，预测误差在0.2 ℃以下的有7个气象站点，取得了较高的预测精度，这主要是因为江西省气象站点数量较多，分布较为均匀，使得反距离权重法能够较为理想地表现气温要素的分布规律，减小插值误差；使用张力样条函数插值法，瑞昌、都昌、永新三个地区的插值结果与实测值误差大于1 ℃，预测误差在0.2 ℃以下的有9个气象站点，由于张力样条函数插值的局部地区气温误差较大，甚至超过了2 ℃，增大了误差，使得其整体误差大于另外两种插值方法，这主要是由于张力样条函数法很大程度上依赖于插值数据，且在边界地区容易受到影响，加之拟合表面连续光滑，过于理想化，造成误差偏大的结果；由于江西省地区的气温分布具有较好的空间自相关性，使用普通克里金法，只有永新地区的插值结果与实测值误差大于1 ℃，预测误差在0.2 ℃以下的有7个气象站点，整体插值效果较好。

三种插值结果中，进贤站和铅山站的预测误差都较小，这说明：这三种插值方法对于上述两个地方的插值研究都较为理想。作为检验点的十个观测站的平均海拔为106.775 m，而进贤观测站的海拔高度为34.2 m，铅山观测站为55.1 m，均远小于平均海拔，海拔高度对于插值效果具有一定影响。余干地区的观测站海拔为21.1 m，为十个观测站中海拔最低的观测站，但只在反距离权重法插值情况下误差较小，从气象站点分布情况来看，进贤站和铅山站周围气象站点数量较多，余干地区气象站虽然海拔最低，但周围气象站点数量不如进贤和铅山地区，导致误差增大。

以表1的站点实测值与不同插值方法的预测值为基础，在Excel表格中进行MAE、MRE和RMSE的计算得到不同空间插值模型的精度比较(表2)。

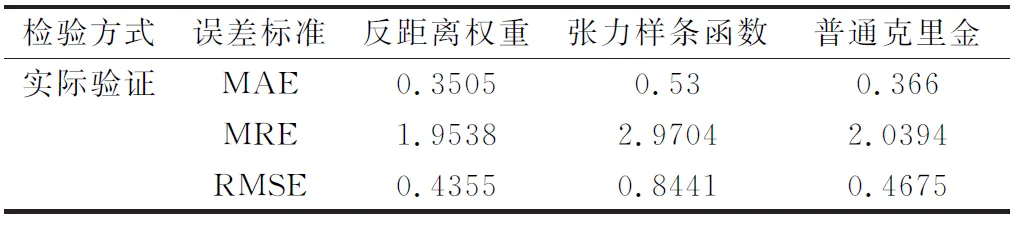
表2 不同空间插值模型的精度比较

从表2可以看出，不同的插值方法其预测结果存在的误差明显不同，张力样条函数插值法无论是MAE还是MRE、RMSE，其对研究区的估算误差均大于另外两种插值方法。对于普通克里金法和反距离权重法的实际验证结果，两者的误差大小比较接近，但是，基于空间距离加权的反距离权重法的预测误差在整体上要更小，其气温数据分布更加平缓，在这三种插值方法之中整体精度最高，由此，反距离权重法的插值结果最符合江西省实际气温的分布。

江西省除北部较为平坦外，东、西、南三面环山，中部丘陵高低起伏，大部分地区海拔高度都在300 m以下，地形对气温的影响较弱。三种插值结果表明，江西省的年平均气温呈现出由北向南逐渐递增的分布特征。验证站点都昌站(58517)上张力样条函数插值精度最低，这表明气象站点较稀疏时对张力样条函数影响较大；铜鼓站(57694)上反距离权重法插值精度最低，说明反距离权重法的插值精度很大程度上受已知点与插值点之间的距离所决定。由于研究区整体海拔不高，气象站点数量较为可观，且空间分布总体较为均匀，因此，三种插值方法误差都不大，但反距离权重法更适宜用于江西省进行空间插值研究。

3.3 不同海拔地区插值效果分析

本文3.2部分对三种插值方法的插值精度进行了比较，可知在上述三种插值方法中，反距离权重法的插值效果最优，因此以反距离权重法的空间插值结果作为数据基础，将20个预留的检验站点按观测场海拔高度不同分为两组(表3)：第一组为观测场海拔高度大于100 m的气象站点，共10个；第二组为观测场海拔高度不足100 m的气象站点，同样也是10个。分别计算第一二组的MAE、MRE和RMSE。

表3 海拔高度不同的实测气温与预测气温比较

由表3可知，MAE：第一组>第二组，分别为0.437、0.264；MRE：第一组>第二组，分别为2.4113、1.4963；RMSE：第一组>第二组，分为别0.5107、0.3443。第一组的MAE，MRE以及RMSE均大于第二组。由此可见，反距离权重法的插值效果在海拔较低的地方比较高的地方好，海拔高度在一定程度上会影响不同插值方法的插值精度，因此在选择研究方法时也要考虑高程的因素。

4 结论

(1)选取反距离权重法、张力样条函数法以及普通克里金法，基于江西省内外30年的气象站点实测气温数据，对江西省年平均气温进行空间插值运算，以MAE、MRE和 RMSE作为插值结果精度评价的依据。结果表明，张力样条函数插值法的误差最大，反距离权重法和普通克里金法的误差比较接近，都比较小，可以较好地应用于江西省气温的预测。

(2)综合分析得出江西省气温空间插值方法的误差排序为：IDWOK Tension Spline。因此，反距离权重法更适合于江西省的气温空间插值研究。

(3)反距离权重插值方法不能保证适用于其他省份的气温研究，对于如此之多的空间插值方法来说，不存在一种适合于所有地方的空间插值方法。在今后的气温研究中可以多去尝试其他的方法，找出最适合的研究方法，为未来的气象预报、环境研究、农业以及工业生产等领域提供数据支持。