惯性参数对飞翼体自由度颤振特性的影响规律研究

雷鹏轩, 吕彬彬, 余 立, 陈德华

(中国空气动力研究与发展中心, 绵阳 621000)

0 引 言

飞翼布局飞行器在气动升阻比、隐身性能、结构效率等三个方面具有先天的优势，成为下一代军事飞行器平台的首选布局形式。为了充分发挥结构重量优势，新一代飞翼飞行器多采用轻质复合材料，使得飞翼飞行器具有明显的结构弹性，特别是一些大展弦比的飞翼飞行器，其结构弹性振动一阶固有频率在1 Hz或更小，极易与刚体运动短周期模态耦合，在远低于设计限制速度的飞行速度下发生一种动力学失稳现象，造成结构破坏从而飞行器坠毁[1-2]。这种由于刚体运动参与而造成的气动弹性失稳现象被称为体自由度颤振(Body Freedom Flutter, BFF)。

2003年美国空军研究实验室(Air Force Research Laboratory, AFRL)发起了SensorCraft项目[4]。项目中洛·马公司提出的一款飞翼布局无人机SC005，经研究发现体自由度颤振成为限制飞机包线的主要制约[5]，自此掀起了飞翼布局飞行器体自由度颤振问题研究的热潮。2007年洛·马公司在NASA兰利TDT风洞中开展了SC006样机体自由度颤振风洞实验研究[6-9]。此后，2010年AFRL联合洛·马公司提出了建立X-56A飞行演示平台(Multi-utility technology testbed, MUTT)计划[10-14]，其目的之一就是研究体自由度颤振。2015年美国明尼苏达大学开展了飞翼外形(mAEWing1, mAEWing2)体自由度颤振模型设计[15-16]与飞行演示实验[17-18]。此外，在计算研究方面Mardanpour和Richards等人利用NATASHA针对简化的飞翼模型，先后研究了发动机位置以及结构惯性与刚度特性对体自由度颤振的影响[19-20]。

国内可见报道的体自由度颤振实验仅两项，皆为验证性实验。2017年西北工业大学谷迎松等人开展了弹性绳支撑下的平板外形全模飞翼体自由度颤振风洞实验[21]。但作者在文中指出，弹性绳支撑下的刚体模态频率并不为零，因此不符合刚体自由/自由边界条件。同年北京航空航天大学黄超等人开展了半模体自由度颤振及其主动抑制的风洞验证实验[22-23]。

目前国内关于体自由度颤振的实验研究多为原理验证性实验，缺乏参数影响规律研究。体自由度颤振涉及到刚体运动与弹性振动耦合，除了受结构刚度影响外，还受到全机质量惯量特性影响。本文首先开展了体自由度颤振风洞实验，根据实验结果检验了有限元模型及计算方法；其次采用风洞实验与计算相结合的方法，研究了仅俯仰自由以及俯仰沉浮自由状态下惯性参数(质心位置、俯仰惯量)对体自由度颤振特性的影响规律。

1 研究模型与方法

1.1 研究模型

模型外形为中等展弦比飞翼外形，参考了目前体自由度颤振问题研究的主流平面外形(图1)。该平面外形分为机身段、翼身融合段与外翼段三段，半模展长为1.527 m，占试验段84%。

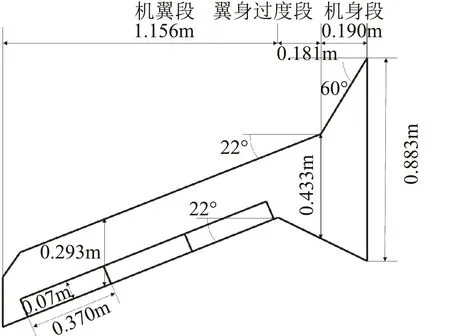
图1 模型平面外形

针对自主设计的模型实物结构，建立了相应的有限元模型(图2)。首先对有限元模型的质量进行了修正，结果如表1所示，装配好的模型重4.49 kg。俯仰转动惯量并未实际测量，而是在质量修正的基础上通过有限元模型核算，约为0.356 kg·m2。

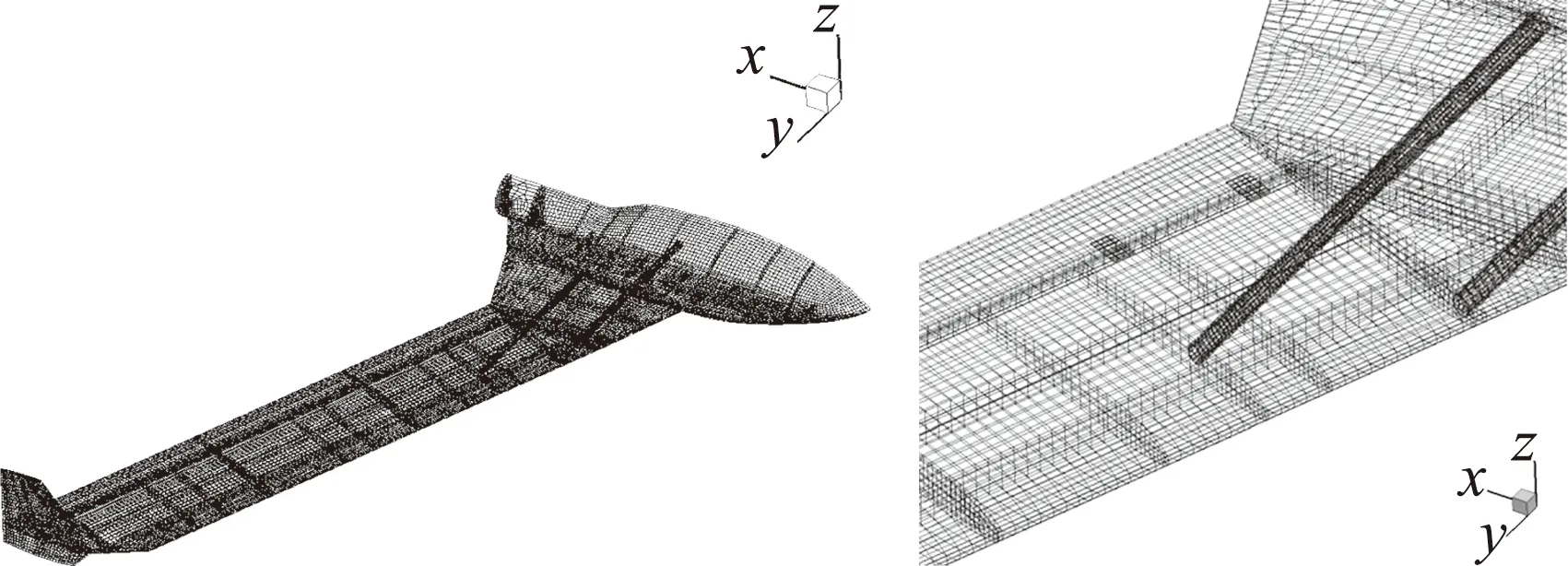
(a)全局 (b) 局部

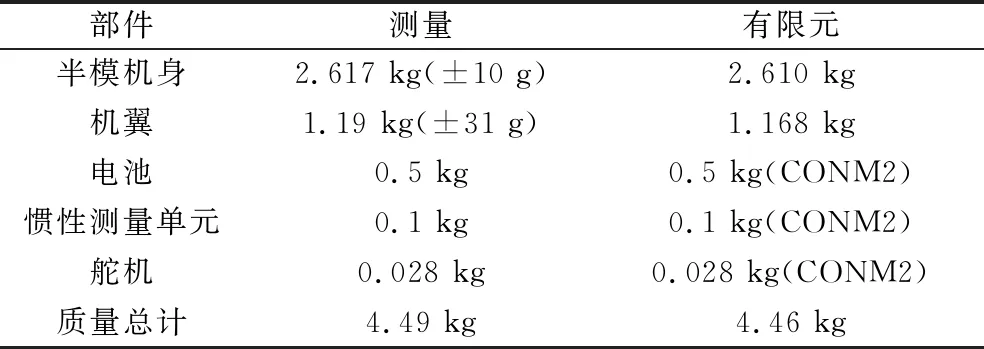
表1 实测模型部件与修正后的有限元模型质量表

其次，对有限元模型的动力学特性进行了修正。在风洞安装状态下开展了地面振动实验，表2给出了修正后的前三阶弹性模态频率对比，可见修正后的有限元模型结构动力学特性与实物是一致的。

表2 地面模态实验结果

1.2 实验与计算方法

本文采用颤振风洞实验和颤振频域计算相结合的方法研究体自由度颤振特性及参数影响规律。风洞实验时仅模拟刚体俯仰运动，模型侧壁水平安装(图3)，模型可绕侧壁上的支撑转轴做俯仰自由转动。采用风洞湍流激励，直吹颤振点获得颤振特性。

图3 模型安装状态

采用应变片和加速度传感器测量模型的动态响应，采样率200 Hz。加速度传感器和应变片分别安装在机翼段的翼梢和翼根。模型机身前部安装有空速管，用于测量风洞风速。模型内部装有惯性测量单元，位于机身内部半模对称面靠近质心位置处，型号为ADIS16488，用来测量机体的俯仰角及俯仰角速度，采样率为25 Hz。

颤振计算采用频域方法，气动力采用偶极子网格法(Doublet Lattice Method, DLM)计算，气动面网格划分如图4所示。采用P-K法求解，马赫数Ma=0.1，空气密度1.145 kg/m3。

图4 气动面网格

2 实验与计算结果分析

表3给出了风洞实验模型状态及车次表。其中，惯量增大状态通过同时在质心前后200 mm处增加配重，增加全机绕质心的俯仰转动惯量，以下简称俯仰惯量。质心前移状态通过调整内部配重，改变质心位置，同时调整支撑转轴安装位置，使得支撑转轴始终支撑在质心位置，需要指出的是，质心前移后全机俯仰惯量增大了约10.6%。

表3 实验车次

2.1 体自由度颤振实验与计算结果对比分析

首先对颤振实验结果进行初步分析，并与计算结果开展对比分析。图5给出不同模型状态下的颤振实验风速阶梯。体自由度颤振发生时由于俯仰姿态大幅运动，安装在机身上的空速管的空速测值瞬间降低。以BFF-01为例，图6与图7分别给出了颤振发生时的俯仰角、应变以及加速度时域与频域响应。其中时域响应以各信号间的迟滞环曲线形式给出，可见弯曲应变与扭转应变同相位，与俯仰角相位迟滞明显，表明这是由弹性模态和刚体模态耦合所发生的颤振，即体自由度颤振。基准状态的颤振频率约为1.70 Hz，各测量信号的频率响应吻合良好。图8给出了颤振发生时的图像，可以明显看到全机俯仰振动的同时伴随着机翼弯曲振动。

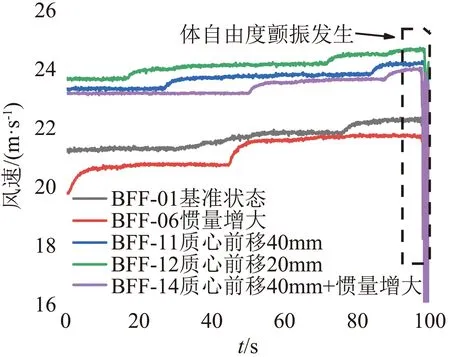
图5 不同模型状态下的颤振临界速度

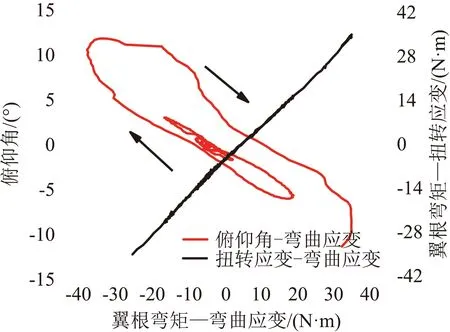
图6 振动信号迟滞曲线

图7 BFF-01次频率响应

图8 颤振发生时图像

表4给出了实验结果与频域计算结果的对比。在变化规律上，对比表4中BFF-01与BFF-06以及BFF-11与BFF-14实验与计算结果可见惯量增大后颤振频率明显降低，颤振速度变化很小，实验结果降低约2%，计算结果增加约0.8%。其次，对比BFF-01、BFF-12(前移20 mm)、BFF-11(前移40 mm)次实验与计算结果，质心位置前移后颤振频率与颤振速度均明显增大。在量值上，计算的颤振速度总体偏高，颤振频率基本一致，最大偏差不超过10%。通过实验与计算结果的对比，有效地检验了有限元模型与颤振计算的可靠性。

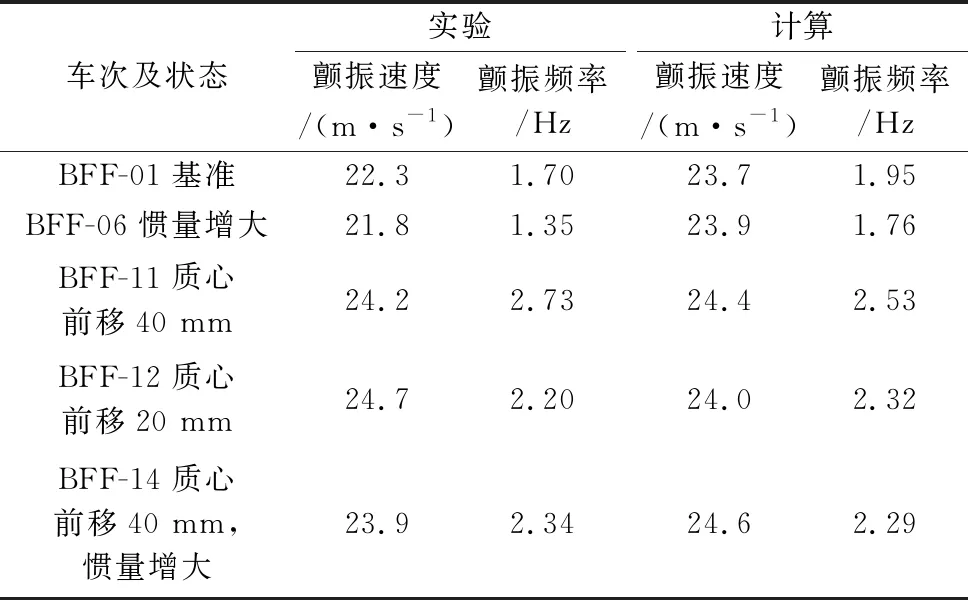
表4 实验与计算结果对比

2.2 俯仰惯量对体自由度颤振影响规律

采用相同的计算模型研究俯仰惯量的影响规律。在质心前移40 mm状态下，保持增加的配重大小不变，计算了配重距质心距离(dx)对体自由度颤振的影响，同时考虑了沉浮约束与沉浮自由两种刚体边界条件。图9给出了颤振计算结果。无论沉浮自由度约束与否，随着配重向质心两侧远离，俯仰惯量增大，俯仰模态频率降低，颤振频率降低。沉浮约束时，颤振速度变化仅0.4m/s。但沉浮自由时，俯仰惯量的影响规律有所不同，随着配重偏移位置增加，颤振速度明显增加。

(a) 沉浮约束

对上述规律进行分析，首先从模态阻尼和频率的变化规律进行分析。图10给出了计算获得的V-g-f曲线。从V-f图中可见，俯仰惯量增大使得俯仰模态频率降低，并远离一弯模态频率，模态间耦合变困难。观察V-g图可见，在30 m/s之前，惯量对俯仰模态阻尼影响很小。因此当沉浮自由度约束时，在颤振点附近，模态阻尼基本不随惯量而改变，因此颤振速度也变化很小。而沉浮自由时，在颤振点附近不同惯量的俯仰模态阻尼走势完全不同，随着俯仰惯量增加，模态阻尼降低，颤振速度明显增大。

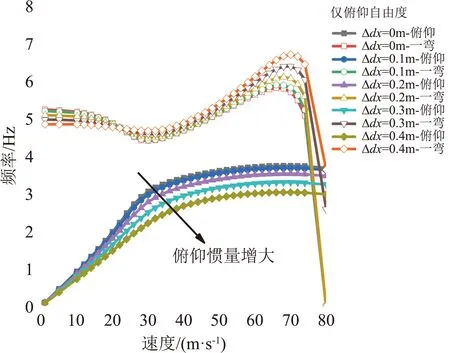
(a) V-f (沉浮约束)

其次，对比不同惯量下的模态振型可见(图11)，当沉浮约束时，随着惯量增大一弯模态节线变化很小，在机身部分由于质心的沉浮位移为零，因此质心始终为一弯振型的一个节点，致使一弯模态节线始终保持与俯仰模态节线相切。相比之下，沉浮自由时随着惯量增大一弯模态节线变化明显。尤其是机身部分的节线位置，随着惯量增大逐渐前移。

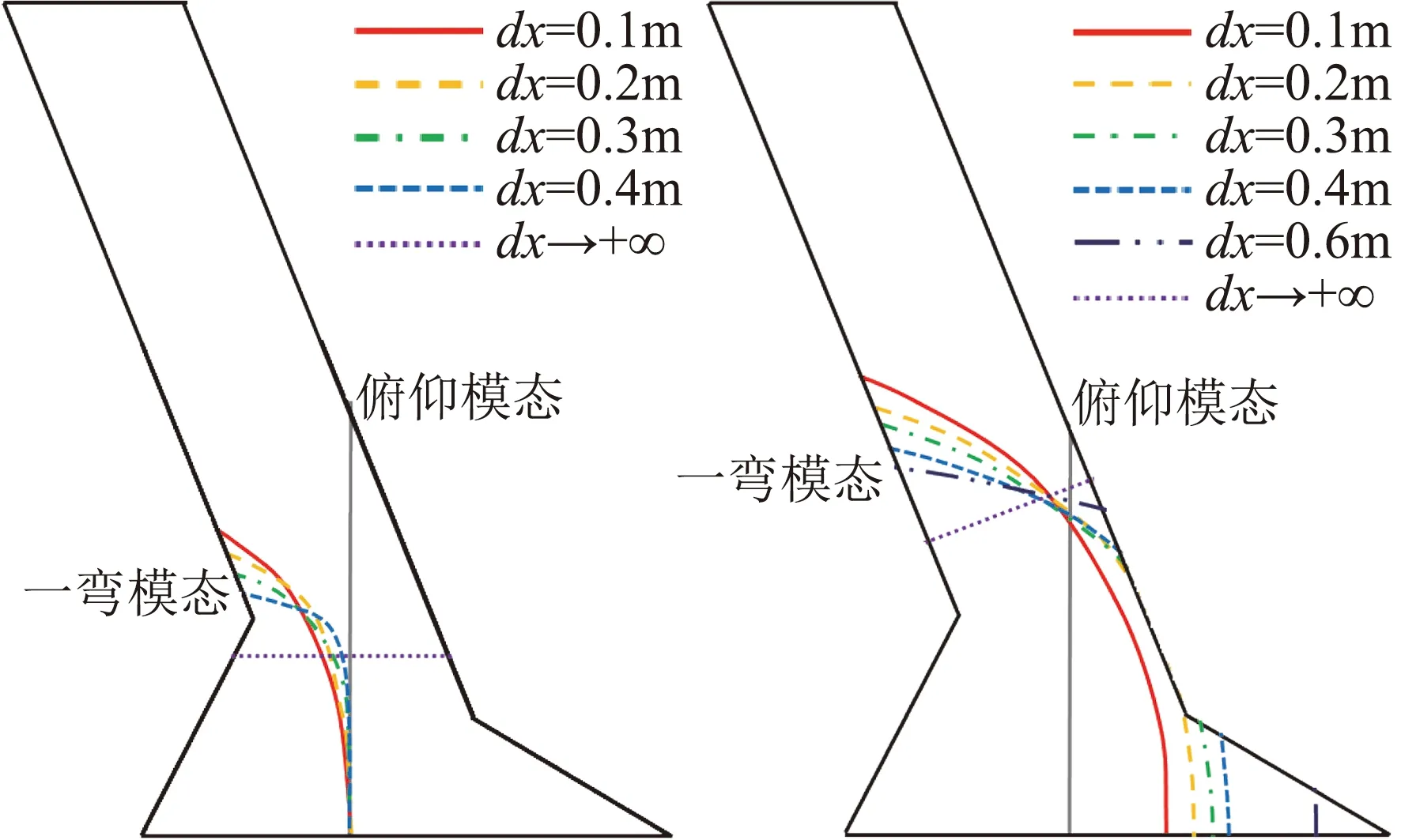
(a) 沉浮约束 (b) 沉浮自由

最后，从气动力做功的角度分析，参照弯扭颤振机理，全机俯仰运动相当于充当了弯扭颤振中扭转变形的角色，由于外翼段的弯曲变形和全机俯仰运动存在相位差，致使一个周期内气动力做正功，系统发散。以此为基础，分析一弯模态的节线可以发现，由于机身部分弹性变形与外翼弯曲变形方向相反，相比于外翼段做正功(加载)，机身变形在颤振时做负功，起到了卸载的作用。对比两种刚体边界条件下的振型不难发现，沉浮约束时一弯模态节线受到质心节点的约束，几乎不发生变化，因此颤振速度未发生明显变化。沉浮自由时，一弯模态节线的变化使机身部分的卸载面积明显增大，因此颤振速度显著增加，随着惯量继续增大，机身的卸载作用更强，则不再发生体自由度颤振(dx>0.6 m)。

2.3 质心位置对体自由度颤振影响规律

采用计算手段进一步研究质心位置的影响规律。图12给出了质心位置影响规律计算结果，计算时通过添加质量单元保证了质心移动过程中全机俯仰惯量不发生变化。由图可见，随着质心位置由焦点逐渐前移，颤振速度先降低后增高，颤振频率逐渐提高并趋于定值。沉浮约束时颤振速度变化幅度较小，而沉浮自由时颤振速度变化幅度较大。

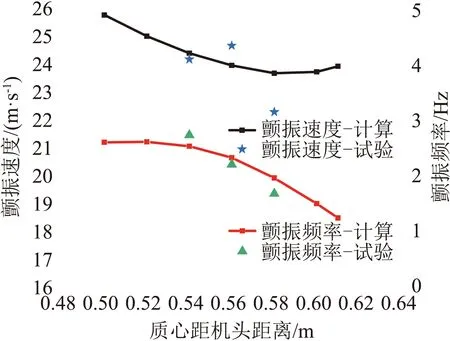
(a) 沉浮约束

将体自由度颤振视为弹性变形影响下的短周期模态失稳问题，模型的俯仰振动微分方程为：

(1)

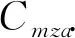
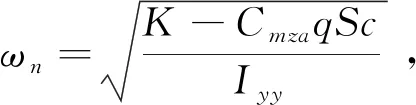
首先结合式(3)对颤振频率变化规律进行分析。图13给出了质心移动前后，式(3)和P-K法计算的模态频率变化规律，其中Cmzα取自文献[24]中给出的相同平面外形的气动力系数。在来流速度增大至颤振发散之前模态频率线性增大，且质心前移后模态频率增大，两种方法获得的变化规律一致。通过式(3)可明确，由于质心位置前移使得Cmzα增大，导致俯仰模态频率增大，由于发散模态分支为俯仰模态，所以最终颤振频率增加。

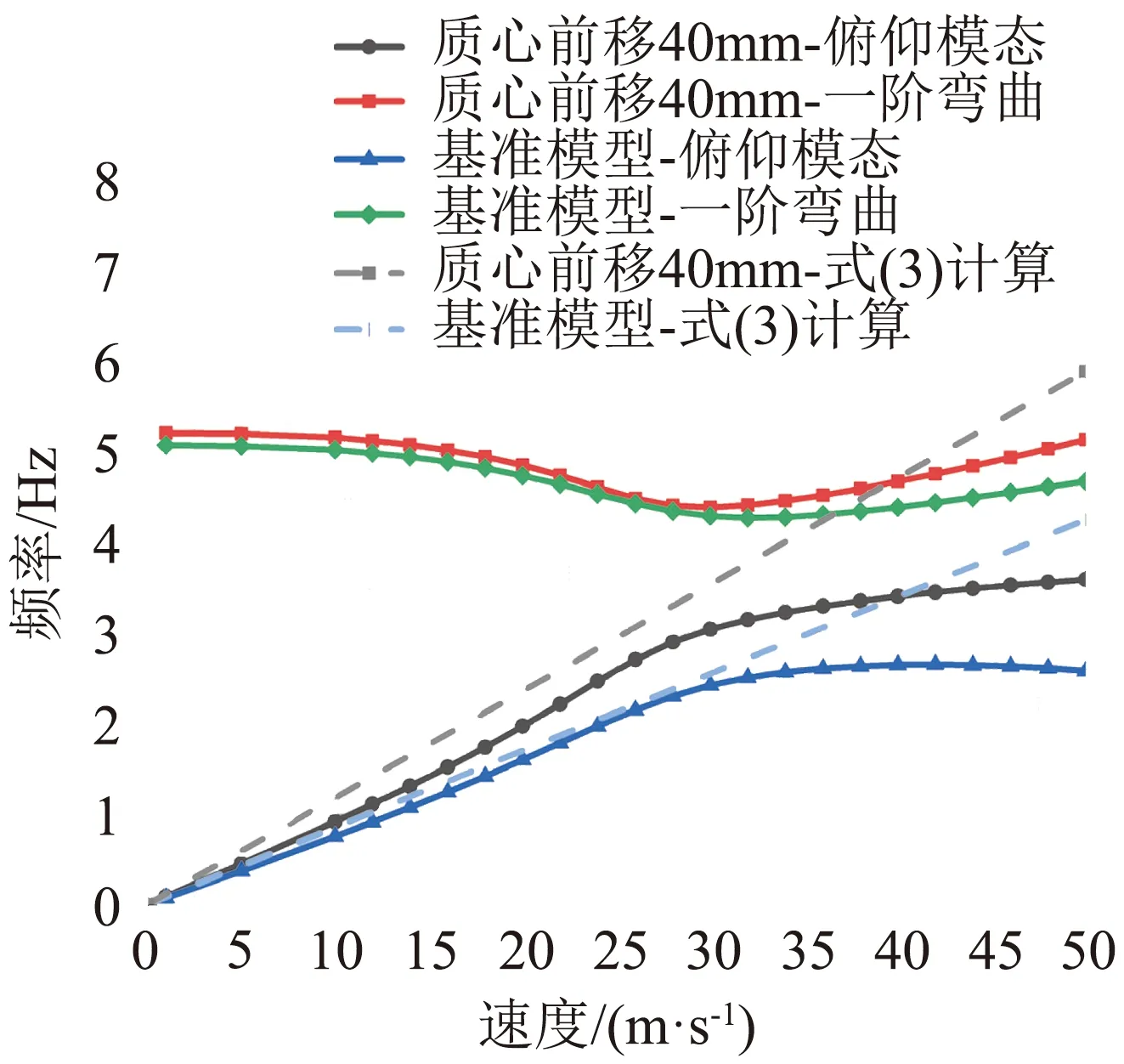
图13 模态频率变化规律

颤振速度由阻尼比决定，根据式(4)可知，质心位置的变化不仅改变了气动恢复力矩，还改变了气动阻尼力矩，因此颤振速度变化规律较为复杂。采用根轨迹曲线进行分析，如图14所示，不同质心位置的俯仰模态极点原点连线与负实轴的夹角代表阻尼比ξ的大小，极点在虚轴上的投影距离表示无阻尼自然频率，根轨迹反映出了俯仰模态特性的综合变化规律。由于俯仰模态参数完全来自气动力矩，其变化同样可以说明气动特性对颤振的影响规律。

图14 不同质心位置的俯仰模态根轨迹图

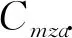
3 结 论

1) 本文开展了惯性参数对飞翼飞机体自由度颤振特性影响规律实验与计算综合研究。风洞实验与计算获得的参数影响规律具有较好的一致性；

2) 俯仰惯量影响规律表明：俯仰惯量增大，俯仰模态频率降低，颤振频率降低，沉浮约束时颤振速度基本保持不变，沉浮自由时，颤振速度增加；

3) 质心位置影响规律表明：质心由焦点前移，俯仰模态频率与模态阻尼同时增加。在初期，模态频率增量较大，俯仰与一弯模态频率靠近，耦合更容易，颤振速度降低，其影响机理和俯仰惯量是一致的；随着质心位置继续前移，俯仰模态频率趋于稳定，模态阻尼影响更为重要，受模态阻尼增加的影响，颤振速度增加。整个质心前移过程中颤振速度先降后增，颤振频率单调增加。