基于AFOA的降噪源分离在轴承复合故障诊断中的试验研究*

刘 畅,金 京,王衍学*

(1.北京建筑大学 机电与车辆工程学院,北京 100044;2.北京建筑大学 城市轨道交通服役性能保障北京市重点实验室,北京 100044)

0 引 言

滚动轴承是旋转机械中的重要传动部件,其健康状态对旋转机械的正常运转起着重要作用,因此,对轴承故障诊断方法进行研究具有十分重要的应用价值。

轴承的故障信号往往是非线性、非平稳的信号,对这类信号的研究一直是信号处理的热点,但大部分的研究都指向轴承单点故障的诊断,对于非线性耦合较为复杂的复合故障信号研究相对较少。如何进行滚动轴承复合故障的有效分离，对其实际的工程应用具有更重要的意义,但常规的信号处理方法却难以提取滚动轴承的复合故障特征。

降噪源分离(DSS)是指在未知复合源信号组成的条件下,根据信号的相关特征,利用针对性的降噪函数,将观测信号逐次迭代地分解成若干组成分量信号[1]。降噪源分离是一种半盲源分离方法,与一般的盲源分离方法相比,降噪源分离算法的优势在于信号分离框架的泛化性和针对性,能针对不同的观测信号构筑出较优的源分离算法,选取合适的降噪函数,从而在混合信号中提取出令研究人员感兴趣的独立分量[2]。

在国内,HE Q等[4]研究了基于最大后验估计的DSS方法,并将其应用于齿轮箱的故障诊断,但分离矩阵会直接影响DSS方法的分离结果,因而该方法不具有自适应性。陈晓理等[5]提出了基于改进样板去噪源分离的诊断方法,并将其应用于轴承的复合故障诊断,通过对仿真和实验数据进行分析,验证了该方法能够有效地提取轴承的复合故障特征信息,但其分离效果依赖于样板的选择。孟明等[6]提出了集合经验模态分解EEMD和降噪源分离DSS与近似熵相结合的方法,用于脑电信号消噪,并用仿真和实际信号验证了所提方法的有效性,但EEMD算法依然有模态混叠等缺陷,不能分解得到较为理想的分量。

本文将AFOA算法引入到降噪源分离中,提出一种基于AFOA算法的滚动轴承复合故障降噪源分离方法。

1 理论基础

1.1 DSS理论

期望最大化(EM)算法的计算步骤分为两步[7]:

(1)计算源信号S的后验概率:

q(S)=p(S|A,S)p(S)/p(X|A)

(1)

式中:p(·)—概率函数;q(·)—后验概率函数。

(2)寻找混合矩阵Amax:

(2)

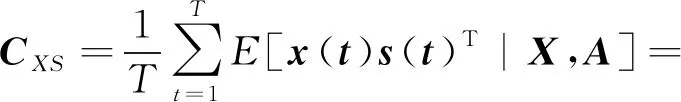
(3)

(4)

式中:T—采样长度。

其中：x(t)=[x1(t),…,xi(t),…,xn(t)];s(t)=[s1(t),…,sj(t),…,sm(t)]。

EM算法中,源信号S的含噪估计可以表示为:

S=ATX

(5)

DSS算法在框架上是基于EM算法的,若源信号间相互独立,结合式(5)可知,源信号S的后验期望E[S/X,A]可表示为关于ATX的函数[8],即:

f(·)=E[S/X,A]

(6)

通常后验概率q(s)的期望Eq(S)可以由概率分布函数p(s)来表示:

(7)

其中:δ由噪声的方差决定。

函数f(·)与源信号S的概率分布有关,而本文中的DSS算法把函数f(·)看成是对源信号的降噪过程。DSS方法的4个核心步骤可以表示为[9]:

s=wTX

(8)

s+=f(s)

(9)

w+=X(s+)T

(10)

(11)

式中:w—分离矩阵W的行向量,表示其中一个源信号的噪声估计;f(s)—构造的降噪函数。

以上各式中,式(8)为计算源信号的噪声估计;式(9)为降噪过程,含此式的源分离方法即为DSS;式(10)为降噪后的s+对分离矩阵w的重新估计;式(11)对w+矢量归一化。

DSS算法在迭代求解过程中,克服了ICA算法先验知识具有全局性的缺陷,对于非线性的混合信号进行了降噪处理,减弱了随机噪声的影响,增强了其特征信息,可以实现更好的分离效果。

1.2 降噪函数的选择

DSS算法关键在于去噪函数的选择。针对一般的非线性混合信号,常用的降噪函数主要有:斜度降噪函数f(s)=s2、峭度降噪函数f(s)=s3、正切降噪函数f(s)=s-tanhs。由于实际采集的信号中含有较多的干扰成分,参考文献[10]指出:对于非线性混合信号,在噪声成分较多的情况下,相比于其他几种降噪函数,正切降噪函数的稳定性较好,受信号中干扰成分的影响程度较低,信号的分离精度更高,鲁棒性更好。同时,正切降噪函数对于非高斯信号也具有优异的降噪效果,因此本文选择f(s)=s-tanhs作为DSS算法的降噪函数。

1.3 Fast ICA算法

快速独立分量分析(Fast ICA)作为独立分量分析(ICA)的改进方法,是基于ICA的固定点迭代递推算法,也是盲源分离的核心方法,其基本迭代公式为[11]:

W(m+1)=

E{Zg[WT(m)Z]}-E{g′[WT(m)Z]}W(m)

(12)

式中:W(·)—混合矩阵;E(·)—期望函数;m—迭代次数;Z—观测信号去均值和白化得到的矩阵,Z=[z1,z2,…zn];函数g(·)—非线性函数,一般可取[12]:g1(x)=xexp(-x2/2)或g2(x)=arctan(x)。

再对W(m1)矩阵单位化可得到:

W′(m+1)=W(m+1)/‖W(m+1)‖

(13)

接下来判断W′(m+1)是否收敛。若收敛,则由算式X=AS可以分离出源信号S的各个独立分量;否则,重复式(12,13),直至W′(m+1)收敛为止。

1.4 改进果蝇优化算法

由于果蝇优化算法(FOA)存在收敛速度不够快、易陷入局部收敛等缺陷,本文采用一种改进的果蝇优化(AFOA)算法,来进行降噪源分离过程中的分离矩阵的优化求解。AFOA算法通过自适应改变步长的方式,使算法在初始化时获得较大的随机步长,可有效提高算法的全局搜索能力,加快收敛速度;同时,在算法优化的后期,可以以较小的步长来提高算法的局部搜索能力,使算法能够跳出局部最优,并经收敛得到更优的目标值。

基于基本果蝇优化算法步骤得出的AFOA算法的优化求解步骤如下[13]:

(1)初始化果蝇种群规模为Sizepop,最大迭代次数Maxgen,随机初始化果蝇群体位置(X0,Y0);

(2)赋予果蝇个体搜寻食物的随机距离与方向,即:

(14)

式中:H—-step(步长)到step间的随机数,在基本FOA算法中step=1。

(3)估计第i个果蝇与原点的距离D,再计算味道浓度判定值S,即:

(15)

(4)求果蝇个体味道浓度(Smelli),即:

Smelli=Function(S)

(16)

(5)找出该果蝇群体中味道浓度最高的个体,以及其相应的浓度值,即:

[bestSmellbestIndex]=max[Smell]

(17)

(6)保留味道浓度最高的果蝇个体的x,y坐标,则果蝇群体向该位置飞去,即:

(18)

(7)重复执行以上步骤(2～5),进行迭代寻优,并判断味道浓度是否优于前一代味道浓度,若是,则执行步骤(6)。

改进果蝇优化算法的自适应步长公式如下所示[14]13:

(19)

式中:i—1到Sizepop之间的整数,表示果蝇群中第i个果蝇;j—1到自变量个数N之间的整数,表示第i个果蝇的第j个自变量的横纵坐标分量;k—自变量横、纵坐标的步长,k=1或k=2;p—当前迭代次数;P—搜索区域的横坐标或纵坐标长度(当j[1,N/2],P—横坐标长度;当j∈[N/2+1,N],P—纵坐标长度)。

果蝇个体的改进位置更新公式如下所示:

(20)

若当前迭代次数中已经连续L代没有寻得最优解,则选择目标函数N个自变量中的Q个自变量进行更新,其他自变量不变。

其更新公式如下:

(1)若当前迭代时的L≤Maxg/p,自变量步长更新公式为[14]14:

(21)

(2)若当前迭代时的L>Maxg/p,自变量步长更新公式为:

(22)

1.5 AFOA-DSS方法

轴承振动信号呈现非高斯分布,而负熵作为熵的修正形式,可以用来度量非高斯性。对于一个混合信号而言,在信号分解过程中,分量信号的非高斯性能表示分离的分量信号间的相互独立性,负熵值越大非高斯性越强,表明分离的效果越好。

负熵的定义如下[15]:

Ng(Y)=H(Ygauss(-H(Y)

(23)

式中:Ygauss—与Y具有相同方差的高斯随机变量;H(·)—随机变量的微分熵。

公式定义如下:

(24)

当Y具有高斯分布时,Ng(Y)=0;微分熵越小,Y的非高斯性越强,Ng(Y)的值就越大。

在计算Ng(Y)时,需要先估计Y的概率密度函数,采用以下近似公式求取[16]:

Ng(Y)={E[g(Y)]-E(g(Ygauss))}2

(25)

式中:E(·)—均值计算;g(·)—非线性函数,本文取g(Y)=tanh(y)。

选择负熵来衡量非高斯性时,要先对信号进行零均值、中心化和预白化处理,以满足E(YYT)=I(I—单位矩阵)的约束条件。

AFOA算法初期已采用批处理和较大随机步长的方式,对降噪源分离的初始矩阵进行了初步优化,得到较优的初始值;以分离矩阵作为果蝇个体,以负熵作为目标函数,以负熵最大作为寻优条件,得到最优分离矩阵,进而得到估计的独立源信号。

AFOA-DSS算法的基本过程如图1所示。

图1 AFOA-DSS算法流程图

2 仿真信号分析

为了验证本文所提方法的有效性,笔者将其应用于滚动轴承复合故障仿真信号源分离中。

复合故障仿真信号如下[17，18]:

(26)

式中:Pi—脉冲数量;Aj—脉冲幅值,Aj=[0.4,1];Ti—冲击周期,T1=0.01 s,T2=0.012 5 s,分别作为仿真内圈故障和外圈故障的冲击周期。

h(t)为冲击脉冲函数:

(27)

式中:β—衰减系数,β=60 Hz;fr—共振频率,fr=200 Hz。

因为实际的轴承振动信号的故障特征信息常被大量噪声所掩盖,在脉冲冲击信号中要加入高斯白噪声n(t)。笔者设置采样频率fs=20 kHz,采样点数为10 000点;由冲击周期计算出内圈故障特征频率fi=100 Hz,外圈故障特征频率f0=80 Hz;将内圈仿真源信号s1和外圈仿真源信号s2分别加入相同的高斯白噪声n(t)，再分别与二阶随机矩阵A相乘得到混合信号，即观测信号,以构成源分离所需的基本模型。

观测信号波形图如图2所示。

图2 观测信号波形图

由观测信号可以看出,内圈和外圈故障冲击特征被完全淹没在噪声信号中。

利用AFOA优化DSS分离矩阵的过程如图3所示。

图3 AFOA优化过程图

由图3可知:利用AFOA-DSS优化过程中,当迭代次数为100,负熵值为8.9时,得到了最优的分离矩阵;而AFOA-Fast ICA优化过程是在迭代次数为160,负熵值为6.3时,得到的最优分离矩阵。因此,该结果表明：本文所提方法可以实现更快的收敛速度,且分离信号的独立性更强。

笔者最后通过基于正切函数的降噪源分离算法对观测信号进行有效分离,得到估计信号波形图,如图4所示。

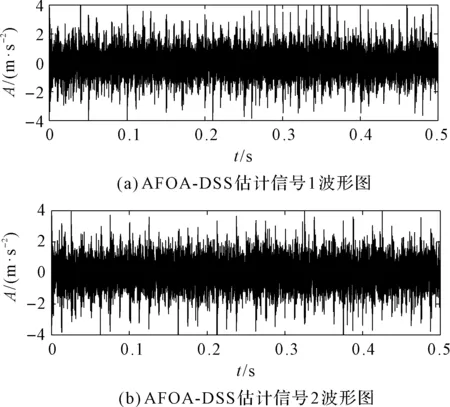
图4 AFOA-DSS估计信号波形图

为了验证所提方法的优越性,笔者将其与AFOA-FastICA的分离结果进行对比分析,如图5所示。

图5 AFOA-Fast ICA估计信号波形图

从图5中可看出:估计信号虽显出一些微弱的冲击特征,但大部分故障信息仍被掩盖;同时,可明显看出,AFOA-DSS算法取得了比AFOA-FastICA算法更好的分离效果。

进一步给出图4所示估计信号的包络谱图,如图6所示。

图6 AFOA-DSS估计信号包络谱图

由图6可知:内圈故障特征频率fi及其倍频处存在明显的峰值;外圈故障征频率f0及其倍频处也存在明显的峰值,其他频率处的幅值都比较小。由此可知,应用本文所提方法能很好地将两个仿真源信号从观测信号中分离出来。

图5所示估计信号的包络谱图如图7所示。

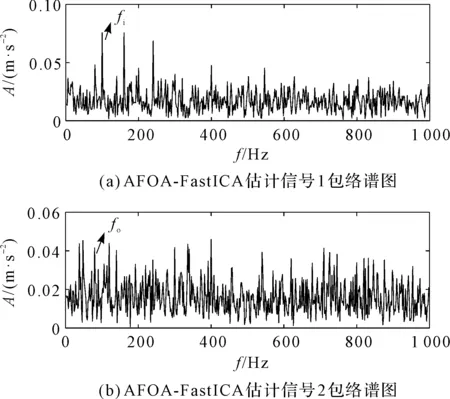
图7 AFOA-Fast ICA估计信号包络谱图

从图7中可看出:内圈故障特征频率fi和外圈故障征频率f0处峰值过低,且周围干扰频率太多,无法准确提取复合故障特征。因此,可以看出本文所提方法效果更好。

为了更客观地评价算法的分离效果,笔者利用分离信号与源信号的相关系数绝对值、均方误差和重构信噪比3种性能指标,来衡量分离效果。

3种性能指标分别定义如下[19]:

(1)相关系数绝对值(AVCC),表示分离信号与对应源信号之间的相似度,其值为[0,1]。AVCC越接近于1,表明分离信号与源信号的相似度越高,分离效果越好。

AVCC表示如下:

(28)

(2)均方误差(MSE)表示分离信号与对应源信号之间的平均误差,其值越接近于0,表明分离效果越好。

MSE表示如下:

(29)

(3)重构信噪比(RSNR)也是评判信号分离效果的重要性能指标。该值越大,表明分离效果越好。

RSNR表示如下:

(30)

自适应果蝇优化算法优化降噪源分离方法,对轴承故障仿真信号的分离和优化效果,与优化快速独立分量分析方法对比结果如表1所示。

表1 AFOA-DSS和AFOA-FastICA分离和优化效果对比

3 实验数据分析

笔者将本文所提方法应用于滚动轴承内、外圈复合故障振动信号进行分析,以验证本文所提方法的有效性和可靠性。

笔者利用MFS-Magnum(MFS-Mg)机械故障综合模拟实验台进行试验。该实验台由1 HP变频交流驱动器、1 HP 3相电动机、手动调速器、9个传感器连接内螺孔的可拆分轴承座、16孔的BNC接线面板、一根直径为3/4 inch的TGP刚制直轴、端部卡圈可拆分的转子、联轴器等组成,可以采集振动数据,进行机械故障的模拟试验。

本文利用该实验台进行滚动轴承复合故障试验,实验台如图8所示。

图8 MFS-Mg实验台

试验采用ER-16K型单列深沟球轴承,安装在直轴中心位置;使用两个加速度传感器(灵敏度为98 mV/g),使用磁性底座将其分别放置在电机壳体驱动端12点钟方向和风扇端12点钟方向,通过16通道VQ数据采集系统收集振动数据;采样频率fs为20 kHz,采样点数为25.6 K。

ER-16K型轴承的规格参数如表2所示。

表2 ER-16K型轴承规格参数

ER-16K型轴承故障相关参数如表3所示。

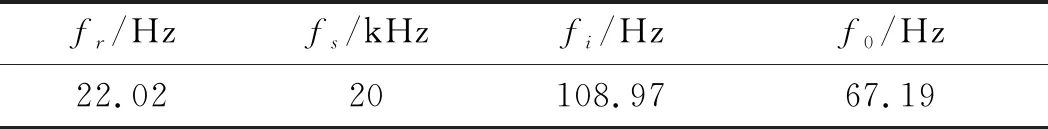
表3 ER-16K型轴承故障相关参数

fr—电机转频;fi—内圈故障特征频率;f0—外圈故障特征频率

观测信号波形图如图9所示。

图9 观测信号波形图

观测信号的包络谱图如图10所示。

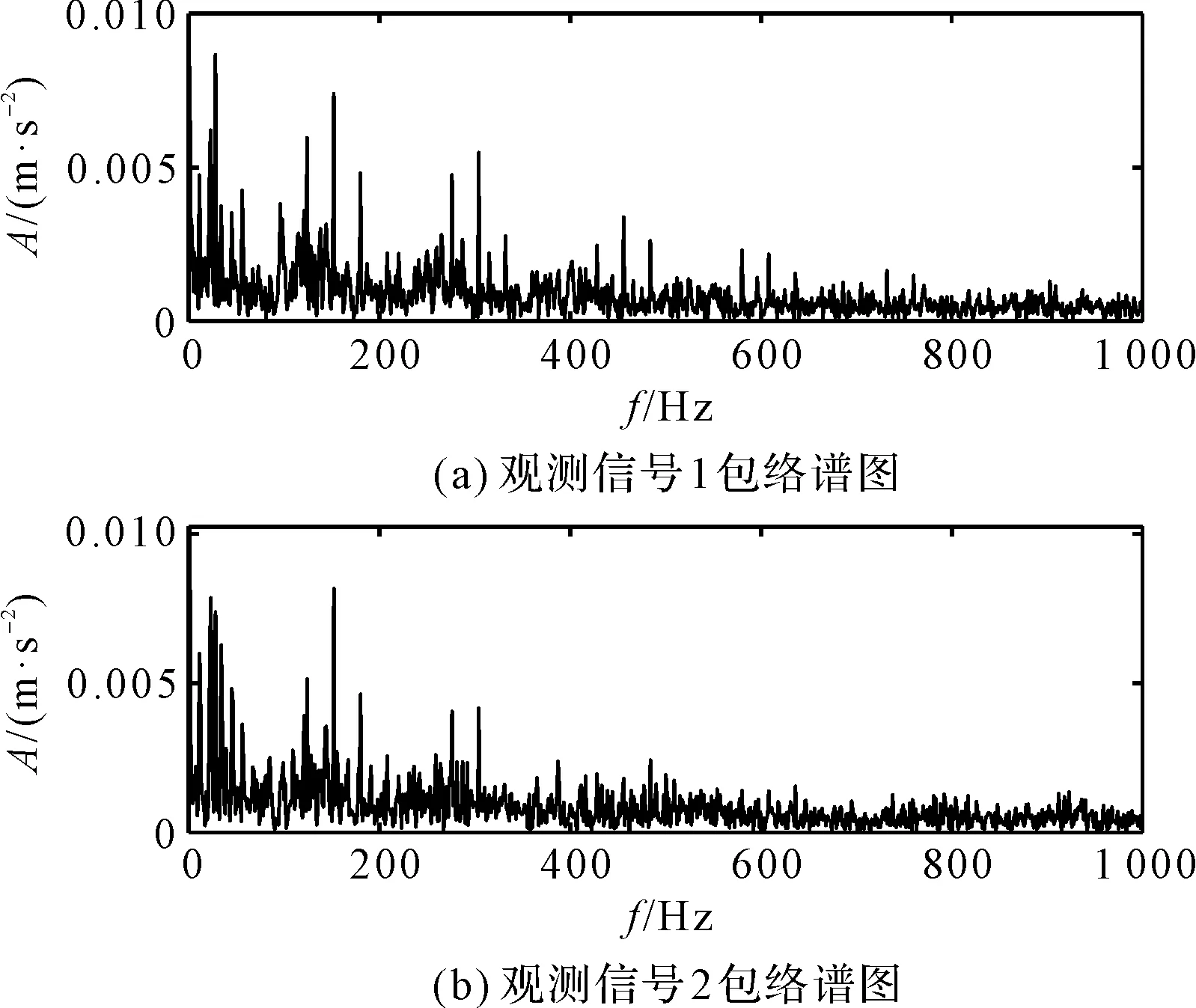
图10 观测信号包络谱图

由图10可知:两个观测信号的包络谱中,都同时存在多个明显的谱峰,但并不是轴承内、外圈故障特征信息,而且故障特征复合在一起不利于故障模式识别。

利用本文所提方法,笔者通过基于正切函数的降噪源分离算法和自适应果蝇优化算法优化分离矩阵的方法,对观测信号进行有效降噪和分离。

优化过程如图11所示。

图11 AFOA优化过程图

由图11可知:利用AFOA-DSS优化过程中,当迭代次数为700时,得到了最优分离矩阵,此时的负熵值为9.7;而AFOA-Fast ICA优化过程是在迭代次数为900,负熵值为7.5时,得到最优分离矩阵。该结果表明:本文所提方法可以实现更快的收敛速度,取得更优的分离效果。

应用基于正切函数的降噪源分离可得到估计信号,如图12所示。

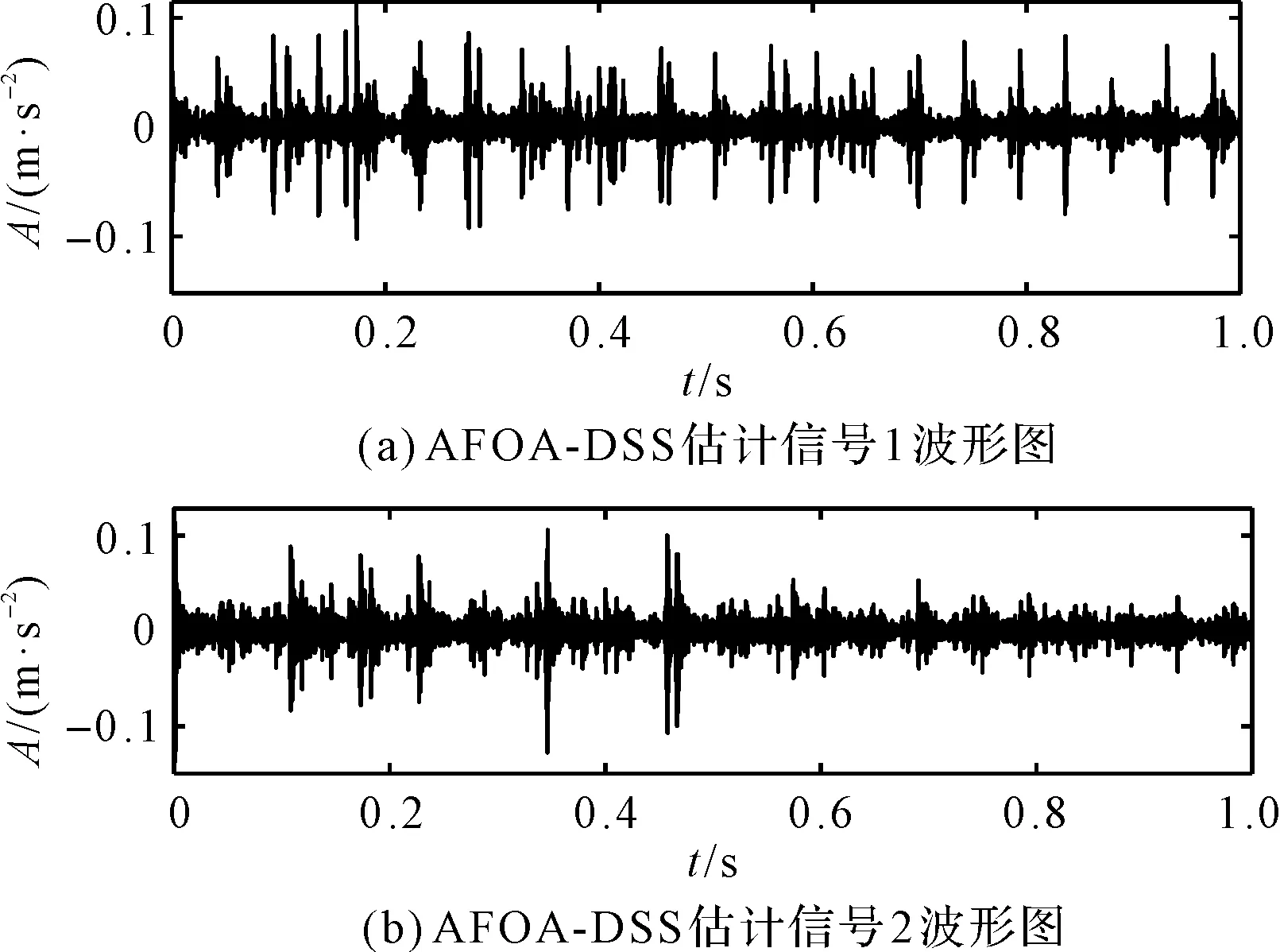
图12 AFOA-DSS估计信号波形图

由图12可明显看出:相对观测信号,估计信号的背景噪声已经大幅度减弱,故障冲击特征十分明显。

对图12的估计信号进行包络分析,可得到包络谱图如图13所示。

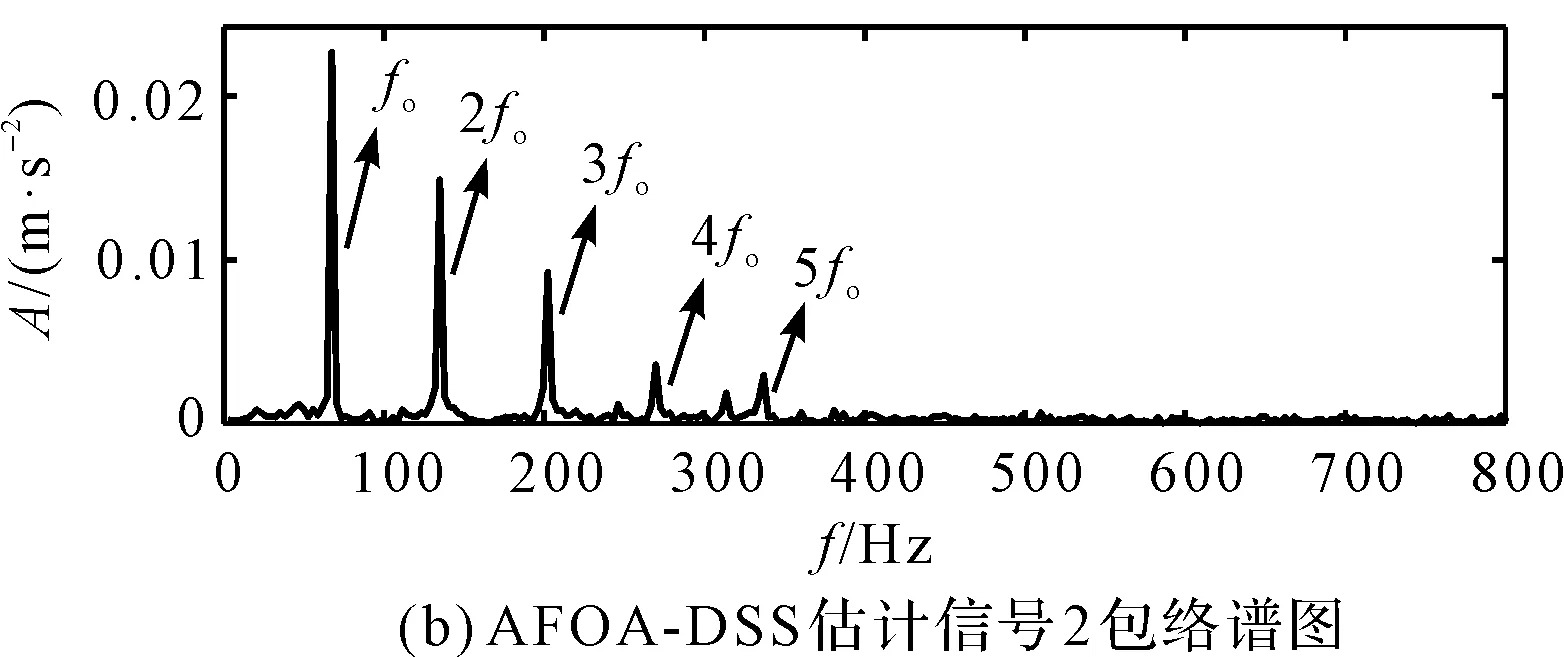
图13 AFOA-DSS估计信号包络谱图

由图13可知:内圈故障特征频率、fi二倍频至五倍频处存在明显的峰值,说明该轴承存在内圈故障;外圈故障征频率f0、二倍频至五倍频处也存在明显的峰值,说明该轴承亦存在外圈故障,且周围的干扰频带很少,故障特征提取效果十分明显。

该分析结果与实际情况完全相符。由此可知,AFOA-DSS算法能准确地将轴承内、外圈故障特征信息从复合故障信号中分离出来,从而验证了本文所提方法的有效性。

同样,笔者给出AFOA-FastICA的估计信号结果,如图14所示。

图14 AFOA-FastICA估计信号波形图

AFOA-FastICA估计信号的包络谱图如图15所示。

图15 AFOA-FastICA估计信号包络谱图

从图15中能看出内圈故障特征频率fi及二、三倍频,和外圈故障征频率f0及二倍频,但峰值不明显,且周围干扰频率很多,无法准确提取故障特征。因此,该结果证明本文所提方法效果更好。

自适应果蝇优化算法优化降噪源分离方法,对实测故障轴承信号的分离和优化效果,与优化快速独立分量分析方法对比,如表4所示。

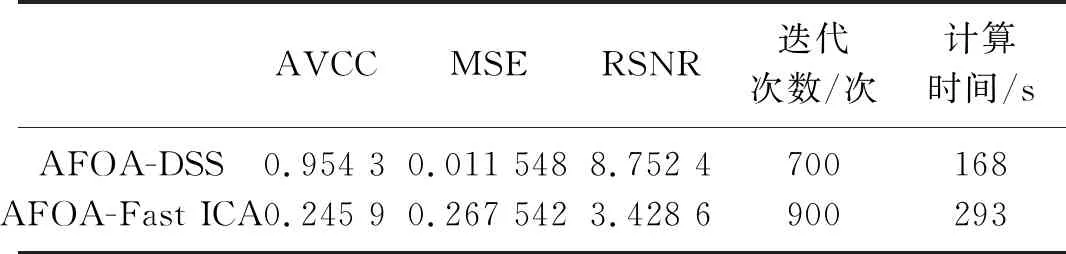
表4 AFOA-DSS和AFOA-FastICA分离和优化效果对比

4 结束语

为有效分离提取出滚动轴承复合故障信号的故障特征,本文提出了一种基于改进果蝇优化算法的降噪源分离方法;通过自适应果蝇优化算法对基于负熵的目标函数进行寻优,得到了降噪源分离的最优分离矩阵,然后通过基于正切降噪函数的降噪源分离方法对观测信号进行了分离,得到了估计源信号,并作包络谱分析识别非线性复合故障特征,实现了对滚动轴承复合故障的特征提取。

仿真实验结果表明:与AFOA-Fast ICA算法相比,AFOA-DSS算法对于非线性复合故障信号具有更好的分离效果;采用AFOA-DSS算法能将轴承内、外圈故障特征从轴承内、外圈混合故障信号中分离出来,准确地识别出轴承内、外圈的故障特征频率;该结果说明降噪源分离方法要优于一般盲源分离方法,并且AFOA算法在寻优性能、算法收敛性和运算速度方面,也明显优于一般的群智能优化算法。

由于信号分析方法根据所研究的滚动轴承的类型不同,采集到的振动数据不同,振动特征的不同,其试验结果一般不相同。

本文的研究对象为单列深沟球轴承,因此,笔者所提的方法具有一定的局限性。而研究通用性的分析方法，即将该方法有效地应用于其他类型轴承，则是笔者未来研究工作的一个重要方向。