基于积分滑模控制的风电机组最大功率跟踪及恒功率控制

乔焰辉，郝诗源，郝万君，尚友涛，王 昊，孙志辉

（1.苏州科技大学 机械工程学院，江苏 苏州 215009；2.丹麦科技大学 电气工程系，哥本哈根 灵比2800；3.苏州科技大学 电子与信息工程学院，江苏 苏州 215009；4.吉化集团有限公司包装制品厂，吉林 吉林 132021）

随着风力发电机组向着大型化、高参数化方向发展，对风力发电机组风能利用率、输出电能品质和运行平稳性的要求也越来越高[1]。然而，风力发电机组是具有高复杂度、强非线性、结构柔性化等特征的机电集成系统，其空气动力特性会随着自然环境的变化而动态改变，具有较大的不确定性。建模误差、参数时变和未建模动态等使得风电机组的精确控制非常困难[2-3]。

针对上述问题，文献[4]根据风电场风速统计概率与Bladed 软件辨识参数，建立了风力发电机组变增益PI 控制器参数整定与优化方法。文献[5]提出一种在全风速范围内同时采用变桨和变速控制来调整发电机输出有功功率的滑模控制策略，在降低风电机组输出有功功率的波动方面具有良好的效果，但牺牲了风能的利用效率。文献[6]为提升双馈风力发电系统直流侧电压平稳性、最大风能跟踪等性能，提出一种基于指数趋近律的滑模变结构控制策略。文献[7]在综合分析风速限功率控制特性基础上，提出一种主动变速和桨距角控制相结合的新型限功率控制策略，充分利用了机组转动惯量，在一定程度上提高发电量。文献[8]推导出了最优桨距角随叶尖速比偏离程度变化的规律，并提出一种额定风速以下的转矩—变桨协调控制策略。

笔者在分析风电机组的机械、电气特性基础上，根据风电系统在高、低风速段的不同控制目标要求，结合滑模控制在处理不确定性和抗干扰的优势，给出ISMC 和ISMC+PI 控制两种策略。并通过仿真实验验证了方法的可行性和有效性。

1 风力发电系统模型

变速变桨风力发电系统由空气动力系统、传动系统、发电机系统、变桨/转速控制器、变桨执行器及参数测量环节等部分组成，如图1 所示。在自然风的推动下空气动力系统会持续旋转，将风能转化为机械能；传动链系统将低转速转变为高转速；发电机系统的作用是将高转速的机械能转化为交流电能，然后经过电力电子电路变换后输送到供电电网；变桨/转速控制器是风力发电机组的核心控制单元，它依据系统的预期控制目标和控制策略对系统的运行状态及参数进行调节与控制；参数测量和变桨执行器分别为检测环节和执行机构。

图1 风力发电机组的总体结构图

1.1 空气动力系统模型

以一种具有柔性水平传动轴的气动风力机为例，运用空气动力学、转子动力学和电机学等方面理论建立该系统的连续动态模型[9]。

当有效风速为v（m/s）的自然风沿轴向吹过风轮机时，风轮机实际捕获到的有效风功率为

式中，ρ 为空气密度，Α 是风轮扫过的区域面积，Cp（β，λ）为风功率的利用系数，其表达式为

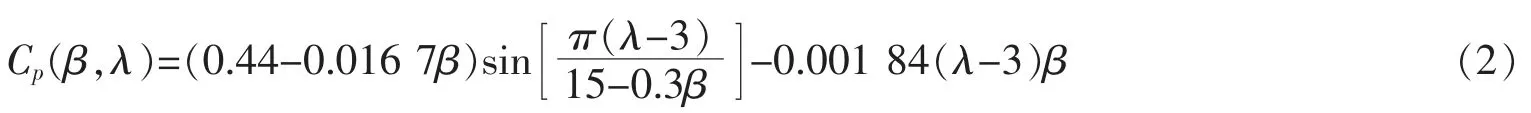
Cp（β，λ）是以叶片桨距角β 和叶尖速比λ 为自变量的函数，且有λ＝Rωr/v。其中ωr为风轮转子的角速度，R 为风轮半径。

风轮气动力矩Ta可以直接从公式（1）推导出来

1.2 传动链系统模型

对于非直驱式风力发电机组而言，从风轮转子到发电机的动力传递是通过传动链系统来实现的，它由低速轴、齿轮变速箱和高速轴连接而成，其模型可用以下一阶微分方程来描述[10]

气动力矩Ta驱动低速轴以角速度ωr旋转，经过齿轮变速箱将角速度提升到高速ωg，其传递与转换后的转矩Tg来带动风力发电机旋转并发电。Jr和Jg分别为低速轴侧（含风轮转子）和高速轴侧（含齿轮箱、发电机）的转动惯量，θ 为高、低转速轴间的扭转角，Hls和Dls分别表示传动系统的转矩硬度和阻尼系数，Kr、Kg分别为低、高速轴的黏性摩擦系数，Ng为齿轮箱转数比。

由（4）、（5）式，消除中间变量θ 可得

若忽略功率损耗，发电机输出功率为

2 风电系统的控制目标

风电系统根据自然风速的不同，大体可划分为切入区、低风速区、过渡区和高风速区，不同风速运行区的控制目标略有不同[10]。其中低风速运行区的控制目标是实现风能的最大功率跟踪（MPPT），即在保持桨距角固定（0°附近）情况下，通过改变发电机转矩来调节风轮转速ωr，以取得最佳的叶尖速比λopt，从而实现风力机捕捉风能的最大化。在高风速运行区，主要控制目标是将发电机功率Pg和发电机转速ωg尽可能地稳定在额定参数附近。此时系统有两个控制器，分别通过调节桨距角给定值βref和发电机转矩给定值Tg，ref来加以实现。

3 积分滑模控制器和PID 控制器设计

3.1 风轮转速的积分滑模控制器设计

滑模控制（Sliding Mode Control，SMC）又称变结构控制，其基本原理是通过设计滑模切换函数和趋近控制率，使系统按着给定的趋近率从初始位置运动到滑模切换面，然后保持系统的运行轨迹沿着切换面滑动至原点[6]。

考虑（1）-（7）式描述的非线性风电系统，其控制目标是当存在不确定性和随机干扰的情况下，使系统的某个输出量y 能够快速地跟踪给定期望值yref，同时使跟踪误差变化率也是收敛于零。

3.1.1 积分滑模切换函数设计

根据系统的控制目标，设计滑模切换函数

其中，c 必须满足Hurwitz 条件，即c>0，其数值的大小决定了误差的指数收敛速度。

为进一步改善控制系统的跟踪性能和消除稳态误差，将积分作用加入滑模切换函数设计，则有

其中ki是积分滑模增益。

3.1.2 系统的李雅普诺夫稳定性

根据控制系统的稳定性准则，可选取以下形式的Lyapunov 函数

保证系统稳定的充分条件是Lyapunov 函数的导数小于等于零，代入（9）式可得

满足系统稳定性的条件是V˙≤0（且仅当S（t）=0 时，V˙=0），其等价条件为

ueq用于控制整个系统运动行为，即跟踪控制；usw用于克服系统不确定性和各种干扰。

3.1.3 等效控制律（ueq）设计

对于风轮转速控制，其跟踪误差可定义为

将上式代入（11）式，可得

将（6）代入上式，最终可以得到

由上式得出等效控制律为

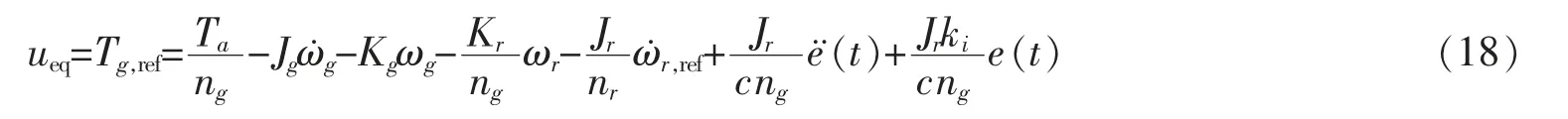
3.1.4 切换控制律（usw）设计

为了满足到达条件，并保证正常段运动的动态性能，采用指数和幂次趋近律的控制律设计方法，可以表示为

式中，sgn 表示符号函数，表示为

其中，-ηS 为指数趋近项。在指数趋近过程中，趋近速度从一个较大值逐步趋向于零，收敛速度取决于系数η。由于单纯的指数趋近，运动点逼近切换面是一个渐近的过程，不能保证在有限时间到达，为此增加了幂次趋近率项k|S|αsgnS。其作用是使得S 趋近于零时，趋近速度是k（ε）|S|α，而不是零。通过调整该系数值，可以保证系统状态远离滑动模态（S 较大）时，能以较大的速度趋近于滑动模态；当系统状态趋近滑动模态（S 较小）时，保证较小的控制增益，以降低发电机转矩的抖振。因此，该系数的取值不仅要与风轮转速密切相关，还应该能够充分反映发电机转矩的波动情况。

当风机以参考风速稳态运行时，发电机转矩Tg接近Tg，opt，即

当风机处于暂态运行时，发电机转矩偏差为

为了抑制发电机转矩的抖振以及可能由此激发的传动系统扭转振动和塔架共振，在幂次趋近律的系数k中引入与发电机转矩的偏差ε 相关的机制，给出了一种新的自适应趋近律的参数定义

kmax、kmin分别为系数k（ε）的最大值和最小值。其设计的目的是随着系统趋近滑模面程度和发电机转矩的波动幅值来自适应地调整增益系数k（ε），以实现更短的到达时间和更小转矩颤振的效果。

由此，切换控制律（usw）可选取为

最终可求得ISMC 控制量为

3.2 （高风速区）发电机输出功率控制器设计

在额定风速区以上时，保证发电机输出功率稳定是风电系统的控制目标之一。此时以桨距控制为主，转矩控制为辅。对于风速的随机快速变化，只有两者很好地结合才能使整机的性能达到最优[11]。

由（1）、（2）式可知，风机系统输出功率与桨距角之间具有复杂的非线性关系，所以桨距角控制不适宜采用上述积分滑模控制策略，所以直接采用PI 控制器。而转矩控制回路仍然采用ISMC 控制。

风机发电功率的跟踪误差定义为

为了取得良好的控制性能，采用粒子群寻优方法获得控制器参数kp、ki。

4 仿真结果及分析

为了验证所提出的控制策略，文中采用Matlab/Simulink 仿真平台建立5 MW 风力发电机组的全阶非线性模型，其主要参数：额定功率为5 MW；齿轮箱变比为97；风轮额定角速度为1.267 1 rad·s-1；风轮转动惯量为5.915 7×107kg·m2；发电机额定角速度为122.909 6 rad·s-1；发电机转动惯量为534.116 kg·m2；风轮直径为129 m；额定风速为20 m·s-1。

忽略自然风的塔影效应和剪切效应，在高、低两个风速段进行系统仿真实验[12]。低风速段的平均风速为7 m·s-1、湍流强度设为20%，如图2（a）所示，其中包括实际风速和估计风速2 条曲线（此段的风速估计采用了文献[13]给出的扩展卡尔曼滤波的风速估计方法）。高风速段的平均风速为20 m·s-1、湍流强度设为12%，如图3（a）所示。

ISMC的控制器参数为：c=25，η=0.52，α=0.65，ki=0.008 9，kmax=0.95，kmin=0.1；PI的控制器参数为：kp=0.005 0，ki=4.56×10-7。将所提控制策略与应用广泛的PID 控制进行性能对比分析。低风速段下ISMC 与PID 控制效果如图2（b）、（c）、（d）所示及见表1。

表1 低风速区的风能转化能力对比

图2 低风速段ISMC 与PI 的控制效果

两种控制策略均能使发电机转速跟随风速变化，达到追踪最大风能的目的。但ISMC 能更有效地跟踪风速的变化，其输出功率和风能利用系数的均值分别为1.48 MW 和0.487 2，比PID 控制高出约4.33%。如图2（c）所示，ISMC 控制在个别时段输出功率低于PID 方法，这是因为部分能量用于转子加速，储存在旋转动能中，此部分动能在风速下降时会得以释放。另外，如图2（d）所示，采用ISMC 控制使得在整个低风速段内风轮转速的波动较小，运行更为平稳。这是因为控制策略中引入了增益自适应调节和抗抖动设计，有效地抑制了风速湍流和随机扰动的影响。

高风速段的风轮转速和输出功率控制采用ISMC+PI 方法，与常规PID 控制的性能对比如图3（b）、（c）、（d）所示。当采用ISMC+PI 控制时，发电机输出功率的最大超调量仅1.1%，采用PI 控制时则有5.3%的超调；在Pg标准偏差（STD）方面，ISMC+PI 只有PID 的1/3 左右，呈现出较好的稳态控制精度，如图3（b）所示及见表2。

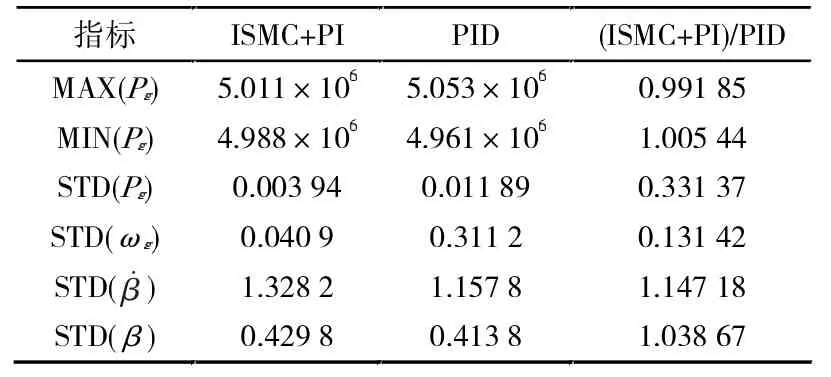
表2 高风速区的性能指标统计

如图3（c）所示，在发动机转速ωg控制方面，相比于PID 控制0.311 2 的标准偏差值，所提控制策略的标准差只有0.040 9，转速波动大大降低，运行更为平稳；但在桨距角及其变化率的标准偏差方面，所提控制策略比PID 控制分别增加了约3.87%和14.7%，这主要是为了及时抑制风速的快速变化，以保证风机输出功率和转速的稳定，实现系统的控制目标，如图3（d）所示。

图3 高风速段ISMC+PI 与PID 的控制效果

虽然增加了变桨距执行机构的疲劳和部件间磨损的风险，但也在执行器工作条件的允许范围内。

5 结语

在分析变速变桨风力发电机组的机电特性基础上，考虑到滑模控制在克服系统非线性、未建模动态和抑制扰动等鲁棒性强的优势，提出了具有自适应趋近率的积分滑模控制（ISMC）策略，并将其用于风电系统在低、高风速段的控制。仿真结果表明，所提出的控制方法能快速地跟随风速的变化和抑制外部扰动，既能提高低风速段的发电效率，又能保证高风速段的风机输出功率的稳定。同时也为下一步高风速区载荷控制研究奠定良好的基础。