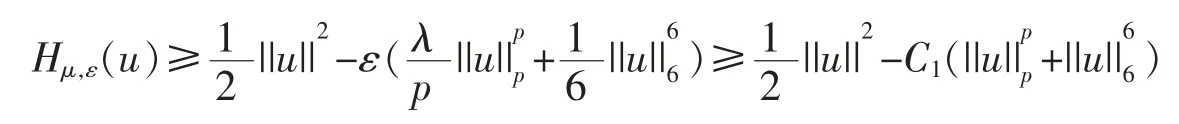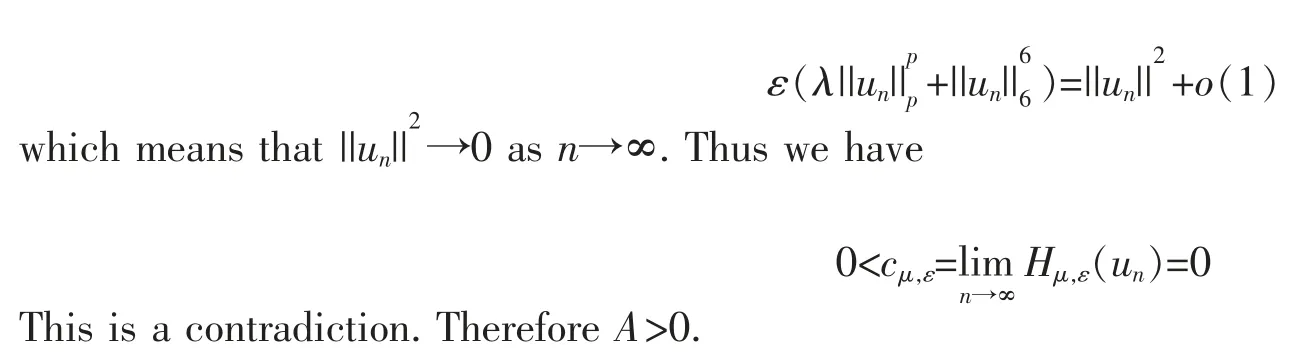Schrödinger Poisson equations with double-critical terms

LIU Zeng

（School of Mathematical Sciences，SUST，Suzhou 215009，China）

Abstract：We studied the Schrödinger Poisson equations with double critical terms -Δu+u+μ（I2*|u|5）|u|3u-λ|u|p-2u-|u|4u=0 in R3，where p∈（2，6）and λ≥0，μ>0，I2（x）:=（4π|x|）-1 is the Riesz potential and * denotes the standard convolution.The existence and nonexistence of positive radially symmetric solutions were obtained by using variational methods.We also explored the asymptotic behaviors of solutions with respect to the parameter λ.

Key words：Schrödinger Poisson equation；critical nonlocal term；Pohožaev identity；variational method

1 Introduction

We are concerned with the Schrödinger Poisson equations with double critical terms

where p∈（2，6）and λ，μ>0.Here I2（x）:=（4π|x|）-1is the Riesz potential and * denotes the standard convolution in R3.

In the last decades，the following Schrödinger Poisson equation

has been widely studied in literatures since it stems from the Hartree-Fock model which appeared in quantum mechanics in the study of a system of N particles.For more information on the Hartree-Fock model，we refer to[1-2].From a mathematical point of view as pointed out in [3]，this model presents a combination of repulsive forces（given by the nonlocal term）and attractive forces（given by the nonlinearity），and this interaction between them gives rise to unexpected situations，including existence，nonexistence，multiplicity results and qualitative behavior of the solutions in the semiclassical limit，see e.g.[3-15] and the references therein.More precisely，Ruiz[13]obtained the existence and nonexistence results of（1）with f（t）=|t|p-2p which depend on the parameter p∈（2，6）and μ>0.Moreover，the author in [13] also showed that p=3 is the critical value for the existence of positive radial solutions.In [16-17]，the authors proved the existence and concentration results.The existence of sign-changing solutions are obtained in [10，12，14].For some other results about existence results for the critical nonlinearity f，see [5,18-23].

However，the papers mentioned above studied the Schrödinger Poisson equations with the subcritical nonlocal term.To the best of our knowledge，the Schrödinger Poisson equation with critical nonlocal term has been studied only in [8，24-25].In [24]，the authors studied problem as（Pμ）with subcritical nonlinearity in a ball domain BR（0）⊂R3.In [25]，the authors studied problem as（Pμ）for general nonlinearity with subcritical growth at infinity and obtained the existence of positive solutions for positive and negative μ respectively by using monotonicity technique，while in[8]，they obtained the existence and nonexistence of positive solutions for different parameter ranges which are completely different from the ones for subcritical nonlocal term.

For the case μ=0，problem（Pμ）becomes the classical Schrödinger equation involving critical growth

（2）has been studied extensively by many authors and the existence of ground state solutions was confirmed，see[18，22，26-28].

Theorem A（cf.[18，22，26-28]）Problem（2）admits a positive ground state solution v0∈C2（RN）∩Hr1（RN）provided that one of the following conditions holds：

（I）p∈（2，2*）and N≥4；

（II）p∈（4，6）and N=3；

（III）p∈（2，4] and N=3 and λ≥λ0，where λ0is a positive constant large enough.

Note that all the papers mentioned above deal with the Schrödinger Poisson equation with either subcritical nonlocal term and critical nonlinearity or critical nonlocal term and subcritical nonlinearity.As far as we know，so far few results are known to the Schrödinger Poisson equation with double-critical case.The main purpose of the present paper is to prove that the existence and nonexistence of solutions for the Schrödinger Poisson equation with double-critical case.

Define the functional Iμ:H1（R3）→R，associated with（Pμ），by

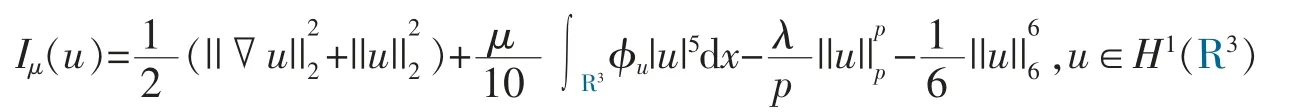
where φuis the unique solution of -Δφ=|u|5in R3.Then Iμis well defined on H1（R3）and is C1class with

It is a standard way to show that a critical point of the functional Iμcorresponds to a weak solution of（Pμ）.Now we establish the following existence and nonexistence results for（Pμ）.

Theorem 1Assume that p∈（2，6），λ≥0 and μ>0.

（I）Let p∈（4，6），λ>0 or p∈（2，4]，λ>λ0，where λ0is given in Theorem A.

（i）Then there exists μ*>0 such that for each μ∈（0，μ*），problem（Pμ）has at least one positive radially solution uμin Hr1（R3）.

（ii）Let uμbe the solution of（Pμ）obtained in（i）.Then，up to subsequences，uμ→u0in Hr1（R3）as μ→0，where u0is a positive ground state solution of the limit equation（2）.

（II）Problem（Pμ）has no nontrivial solution provided

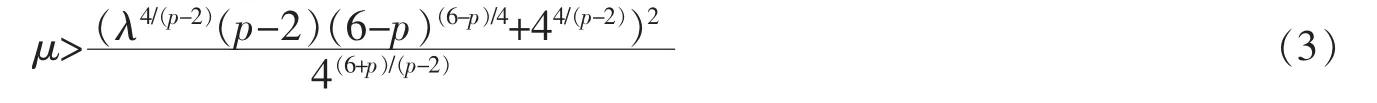
We remark that（I）in Theorem 1 is an analog of the results for（1）obtained in [18，20，22] while（II）in Theorem 1 is new and our results extend some theorems on the cases of the critical nonlocal term and subcritical local term obtained in [8，25] to the double-critical term cases.It is much more difficult to obtain the existence results for problem（Pμ）due to the double critical terms.Firstly，the interaction between the critical nonlocal term and the critical nonlinearity leads to diffculties in proving the boundedness of the（PS）sequences.To deal with the boundedness of（PS）sequences，we use an indirect approach developed by Jeanjean（cf.[30]），a truncation argument（cf.[30-31]）and the Pohožaev type identity.Secondly，the double-critical terms cause a lack of compactness of the Sobolev embedding H1（R3）L6（R3）.

This paper is organized as follows.In section 2，we present some preliminary results and lemmas.Section 3 is devoted to the proof of Theorem 1.

Throughout this paper，we use the standard notations.H1（R3）and D1，2（R3）are the usual Sobolev spaces defined by H1（R3）={u∈L2（R3）:|▽u|∈L2（R3）} and D1，2（R3）={u∈L2（R3）:|▽u|∈L2（R3）}.The corresponding norms and inner products are defined by

Hr1（R3）is the subspace of H1（R3）consists of all radial functions.Lq（R3）is the usual Lebesgue space with the norm ||u||q=（））1/q.In the sequel，S and Cqdenote the best constants of Sobolev embeddings

It is well known that Hr1（R3）Lq（R3）is compact if q∈（2，6）.We use →and ⇀to denote the strong convergence and weak convergence in the related function spaces，respectively.

2 Preliminary

We begin with enumerating some properties of I2*|u|5.The following proposition has been proved in[8] that will be of use throughout the paper.

Proposition 1For every u∈L6（R3），there exists a unique φu=I2*|u|5∈D1，2（R3）which is the solution of

To prove the boundedness of（PS）sequence，as mentioned in Introduction，we use an indirect approach de-veloped by Jeanjean（cf.[29]）as well as a truncation argument（cf.[30-31]）.Define the cut-off function χ∈C∞（R+，R）such that χ（t）=1 for t∈[0，1]，χ（t）=0 for t∈[2，∞），0≤χ（t）≤1 for and | χ′（t）|≤2.For each T>0，we introduce the truncated functional IμT:H1（R3）→R defined by

Now we recall the following abstract theorem（cf.[29]）which we will use in this paper.

Theorem 2Let X be a Banach space equipped with a norm ||·||Xand let I⊂R+be an interval.We consider a family（Hε）ε∈Jof C1-functional on X of the form Hε（u）=A（u）-εB（u），∀ε∈J，where B（u）≥0，∀u∈X，and either A（u）→+∞or B（u）→∞as ||u||X→∞.We assume there are two points v1，v2∈X such that

3 Proofs of main results

In this section，we get the critical point of the functional Hμ，ε.We first show that it satisfies the geometric properties of Theorem 2.

Lemma 4Assume that ε∈[1/2，1] and T>0.Let λ>λ0if q∈（2，4]，λ>0 if q∈（4，6）where λ0is given by Theorem A.Then there exists μ0>0，independent of ε，such that for every μ∈（0，μ0），the conclusions of Theorem 2 hold with 0

ProofBy the Sobolev embedding theorem，we can estimate Hμ，εas

where C1>0 is constant，independent of ε and T，then there exists r>0 and α>0，independent of ε and T，such that for ||u||=r，Hμ，ε（u）≥α.

Remark 2Recall that ε∈[1/2，1] and [1/2，1] is closed interval，then by Step 1，we see that A has a positive lower bound α0>0 and α0is independent of ε.

Step 2There exists μ1∈（0，μ0），depends only on T and S，such that≠0 if μ∈（0，μ1），where μ0is given in Lemma 4.

By a simple calculation，we get a contradiction provided that（3）holds.This completes the proof of Theorem 1.□