基于python算法分析特朗普和拜登对中美经济的影响
2021-06-22王芋钦刘玉婷
卿 枫 周 林 王芋钦 刘玉婷
(西华大学 电气与电子信息学院,四川 成都 610039)
1 问题背景和重述
1.1 问题背景
由于美国总统大选是每四年举行一次。在2020年也会有美国大选,这次的美国大选候选人是特朗普和拜登,他们分别是共和党和民主党的代表人。两人分别在金融贸易,经济金融治理还有一些其他的发展领域,例如对于新冠病毒的措施、基础设施的建设、税收、环境保护、医疗保险、就业、贸易、移民和教育等。他们在对这些方面的问题处理上都有着不同的立场,同时他们在处理这些问题也有不同的行政纲领和政治立场。无论是特朗普还是拜登当选都会对美国的经济发展以及全球经济金融发展形成新的并且是不同的战略格局。不同的候选人当选会对美国有着不同的影响,那么到底会产生怎么样的影响呢?而中国又应该如何去应对这些问题呢?
1.2 开放的问题
1.建立数学模型,利用相关数据定量分析不同候选人当选对美国经济可能产生的影响。(您可以选择一个或者多个字段分别回答此问题或给出一个全面的答案)
2.建立数学模型,利用相关数据定量分析不同候选人当选对中国经济可能产生的影响。(您可以选择一个或者多个字段分别回答此问题或给出一个全面的答案)
3.假设你是中国经济发展智库的成员,结合问题1和问题2的数学模型,在这两种情况下(哪一方获胜),你会对中国在相关领域的经济对策和政策提出什么建议?请具体说明你的观点。
2 问题分析
2.1 问题分析一
首先,问题一我们认为拜登和特朗普的政策会取决于他们背后的两个党派的想法,而党派会以之前的方法继续施行,所以我们打算将之前两个党派分别执政的时候美国的数据提取出来,分成两个数据集,一个是共和党执政期间的数据,一个是民主党执政期间的数据。例如基础设施建设,人均GDP,就业情况等几十个数据集,经过团队的考量与筛选得到了十个数据集,并且对这十个数据集进行数据预处理,数据预处理之后得到的清洗后的数据,再将这十个数据集放入到因子分析模型,得到落石图,并且找到其中的拐点,也就是那几个主要影响美国经济的因子,得到这几个因子过后,我们就可以将其放入我们写好的几个机器学习算法和神经网络模型,得到最后的预测数据,取其中最优的一个模型的预测值,并且分析这样的预测值会对美国的经济产生什么样的影响。[1]
2.2 问题分析二
对于问题二来说,我们将会获取新的数据集,例如分别收集在共和党和民主党两党执政期间的中美贸易量,中国出口贸易量,中国进口贸易量,中国税收等,并且清洗整理数据内容,得到一份完整的数据集,将这份数据集放入到SVR中,得到新的预测值,再利用这个预测值预测两个候选人分别会对中国的经济影响,而两个党派也就是分别代表了拜登与特朗普所会实行的政策。
2.3 问题分析三
对于问题三来说,我们会将之前所得到的影响美国经济几个主要因子中最后的预测数据提取出来,并且这几个数据分别乘以他们的因子系数,而这个值就是我们最后所得到的解,因为我们可以通过这个值来判断究竟两个党派也就是两个候选人所做的事情谁会影响经济正发展的更多,或者谁会导致经济回退也就得到了两党后面会对美国造成的影响,并且选择这个数据大的一位,还有一个问题是对中国的相关经济提出的问题,在我看来,我认为中国的相关领域的经济对策是应当实行反制措施,将中国的教育和医疗水平,公共设施等数据与美国的人均GDP做一个分析,将其相关性为负相和相关性较小的因子提出来,中国则需要大量的提升这些方面的能力就可以了。[2]
3 模型假设
(1)假设从网上获得的数据都是真实可实用的。
(2)假设主要因素是相互独立的,并且不会互相影响。
(3)假设两个党派中仍然会坚持自己的政策方针。
(4)假设没有其他特定的因素影响美国大选。
(5)假设其他候选人被选上的可能性远低于题中所给两位候选人。
4 建立模型并且解决问题一
4.1 数据预处理
为了收集美国相关的数据,我们在很多数据库上进行搜寻,得到了下列的一百多个数据集,为了满足本题所要求的情况,我们将其数据按时间分成共和党执政和民主党执政期间进行处理。
并且我们利用了python对其进行数据预处理,包括在可以用每列的平均值的插入填补空值,重复值的删除、异常值使用3σ原则,最终得到的干净整洁的数据。
最终经过我们的考虑与斟酌,我们留下了九列数据用于相关性分析。
4.2 相关性分析模型的建立
相关性分析python实现。将所有共和党的数据代入python中的相关性分析模型得出其热力图。将所有民主党的数据代入python中的因子分析模型得出其热力图。并且最终将其相关性提出。最终得出影响美国经济较大的几个数据为进出口贸易量、教育人口数、可替代核能和保险服务等。
4.3 BP神经网络模型的建立
4.3.1 BP神经网络的基本原理
BP神经网络即为BackproPagation的缩写,即反向传播的意思,正向传播时,输入样本从输入层传入,经过各个隐层逐层处理后,传向输出层。
4.3.2 BP神经网络的拓扑结构
BP神经网络的拓扑结构如图1所示。
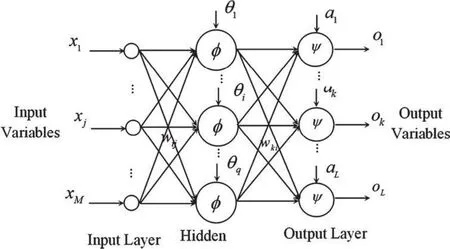
图1 BP神经网络拓扑结构图
4.3.3 BP神经网络的传递函数
我们在这里的BP神经网络用的传递函数是非线性变换函数——Sigmoid函数。因为函数本身及其导数都是连续的,所以非常好处理,并且也较为容易上手:

4.3.4 BP神经网络学习算法

将以上误差定义式展开至隐层,有:
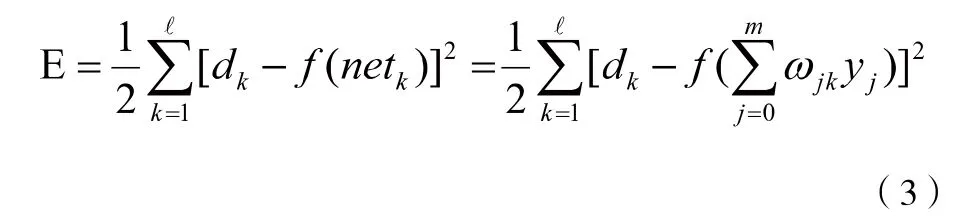
进一步展开至输入层,有:

显然,调整权值的原则是使误差不断减小,因此应使权值与误差的梯度下降成正比,即:
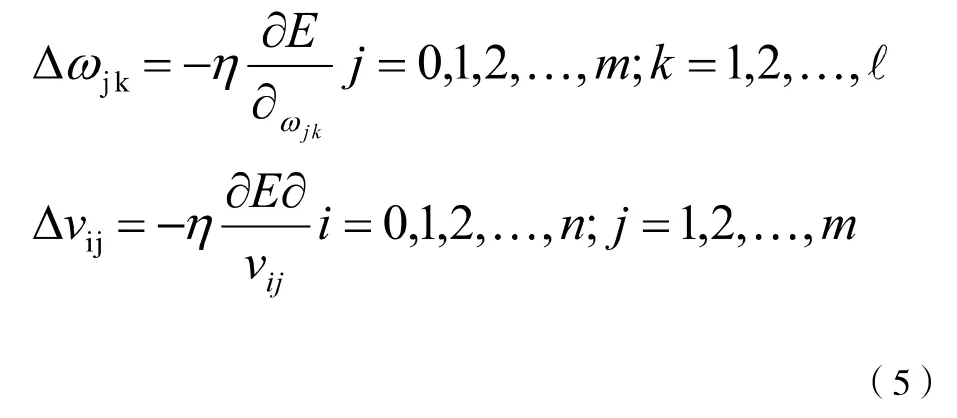
对于一般多层感知器,设共有h个隐层,各个点分别命名为m1,m2,…mh,
各个隐藏层输出分别命名为y1,y2,y3,…yh,矩阵命名为为w1,w2,…wh,wh+1输出层:
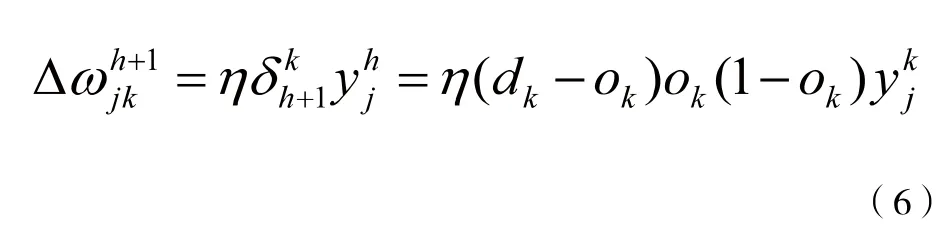
第h隐层:

按以上规律逐层类推,则第一层隐藏权值调整公式
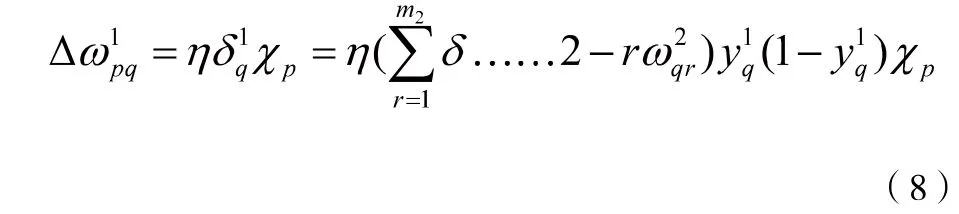
容易看出,BP神经算法中,权值的调整公式均由这几个东西决定,即:学习率,本层输出的误差信号,本层输入信号X(或Y)。
4.3.5 BP神经网络前向传输
我们需要将权重和偏置随机初始化,并且对每一个权重取[-1,1]随机的实数,每一个偏置同样也取[0,1]实数,之后就可以前向传输的运作。
4.3.6 BP神经网络的python实现
本次的我们选择python实现BP神经网络是因为python作为一门开源编程语言,在里面有比较友好的库,例如pandas库可以提供高性能的分析工具,而shuffle则可以随机打乱工具,将原有序列打乱,返回一个全新的顺序错乱的值。
这次的BP神经网络的效果非常的差,因为数据量过少,所以导致了过拟合的状态,但是所幸我们仍然还有其他的选择,BP神经网络只是我们的一种选择,接下来我们将会介绍我们其他的模型。
4.4 SVR模型的建立
4.4.1 SVR模型的支持向量回归
给定训练样本如下:
SVR问题可形式化为:
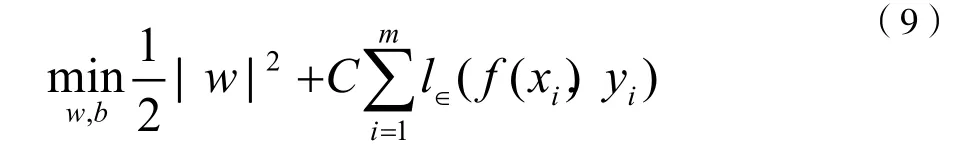


实际中常常采用一种更棒的方法,迭取多个满足条件0<αi 若考虑特征映射形式,则: 4.4.2 利用SVR模型的支持向量回归求解 最终得到的预测值如图2,图3所示: 图2 民主党的预测值与准确值 图3 共和党的预测值与准确值 最终我们得到使用SVR模型中的三种方法,线性、核、径向得出了它的准确率,最终线性的预测效果最高可以达到97.79%,分别为如图4。 图4 SVR模型线性预测准确率 所以使用线性模型进行预测得到的效果是不错的。 4.5.1 决策树的原理 决策树(Decision Tree)是一种基本的分类与回归方法,分类树是决策树在分类时的称呼,回归树是用于回归时的称呼。本文主要讨论决策树中的分类树与回归树的一些基本理论,后续文章会继续讨论决策树的Boosting和Bagging相关方法。[5] 4.5.2 利用决策树解决预测问题 先假设给定的数据集为: 决策树学习是由训练数据集估计条件概率模型。基于特征空间划分的类的条件概率模型有无穷多个,所以我们就可以根据这个方案对我们的数据进行预测。 决策树学习算法包含特征选择、决策树的生成与决策树的剪枝过程。 建立回归树的过程大致可以分为两步: (1)将预测变量空间(X1,X2,X3,...XP)的可能取值构成的集合分割成J个互不重叠的区域{R1,R2,R3,...,Rj}; (2)对落入区域Rj的每个观测值做同样的预测,预测值等于Rj上训练集的各个样本取值的算术平均数。 比如在第一步中得到两个区域R1和R2,R1中训练集的各个样本平均数为10,R2中训练集的各个样本取值的算术平均数为20,则对给定的观测值X=x,若x∈R1,给出的预测值为10,若x∈R2,则预测值为20。 类似于上述决策树分类算法的第(10)步,关键在于如何构建区域划分{R1,R1,R1,...,Rj}。事实上,区域的形状是可以为任意形状的,但出于模型简化和增强可解释性的考虑,这里将预测变量空间划分成高维矩形,我们称这些区域为称盒子。RSS的定义为: 在执行递归二又分裂时,先选择预测变量Xj和分割点s,将预测变量空间分为两个区域{X|Xj<s}和{X|Xj≥s},使RSS尽可能地减小。也就是说,考虑所有预测变量X1,X2,X3,...Xp和与每个预测变量对应的s的取值,然后选择预测变量和分割点,使构造出的树具有最小的RSS。更详细地,对j和s,定义一对半平面: 重复上述步骤,寻找继续分割数据集的最优预测变量和最优分割点,使随之产生的区域中的RSS达到最小。此时被分割的不再是整个预测变量空间,而是之前确定的两个区域之一。如此一来就能得到3个区域。接着进一步分割3个区域之一以最小化RSS。这一过程不断持续,直到符合某个停止准则,如我们在分类决策树中讨论到的前剪枝中的停止准则。[6] 区域{R1,R1,R1,...,Rj}产生后,就可以确定某一给定的测试数据所属的区域,并用这一区域训练集的各个样本取值的算术平均数作为与测试进行预测。 上述方法生成的回归树会在训练集中取得良好的预测效果,却很有可能造成数据的过拟合,导致在测试集上效果不佳。原因在于这种方法产生的树可能过于复杂。一棵分裂点更少、规模更小(区域{R1,R2,R3,...,Rj}的个数更少)的树会有更小的方差和更好的可解释性(以增加微小偏差为代价)。针对上述问题,一种可能的解决办法是:仅当分裂使残差平方和RSS的减小量超过某阀值时,才分裂树结点。这种策略能生成较小的树,但可能产生过于短视的问题,一些起初看来不值得的分裂却可能之后产生非常好的分裂。也就是说在下一步中,RSS会大幅减小。 因此,更好的策略是生成一棵很大的树T0然后通过后剪枝得到子树。 4.5.3 决策树的回归预测算法 1.利用递归二叉分裂在训练集中生成一额大树,只有当终端结点包含的观测值个数低于某个最小值时才停止。 2.对大树进行代价复杂性剪枝,得到一系列最优子树,子树是α的函数。 3.利用K折交叉验诞选择α。具体做法是将训练集分为K折。对所有k=1,2,3,...,对训练集上所有不属于第k折的数据重复第(1)步~第(2)步得到与α对应的子树,并求出上述子树在第k折上的均方预测误差。 4.每个α会有相应的K个均方预测误差,对这K个值求平均,选出使平均误差最小的α。 5.找出选定的α在第(2)步中对应的子树。 4.5.4 利用python实现决策树算法 最终我们得到了决策树对两党的预测准确率分别为66%和59%,如图5、图6所示,所以这个模型也不是特别理想。 图5 共和党预测值 图6 民主党预测值 最终通过比较三个模型我们选择了SVR模型进行预测,因为它的准确率达到了97.79%,并且我们将之前的数据输入得到了两党分别在执政后美国的经济增长情况。 本次的bp神经网络最终得到的效果不是很好,若是数据能够多一些,那么我们便能够预测得到较为准确的数据。 在后来我们仔细的思考了自己的模型,我们认为这次的数据量其实可以使用机器学习中的随机森林,再通过对每个模型的特点进行基于AdaBoost的融合,生成一个融合模型,最终可以用融合模型去预测得到最后的数据,这样可以将准确率再次向上提升几个百分比。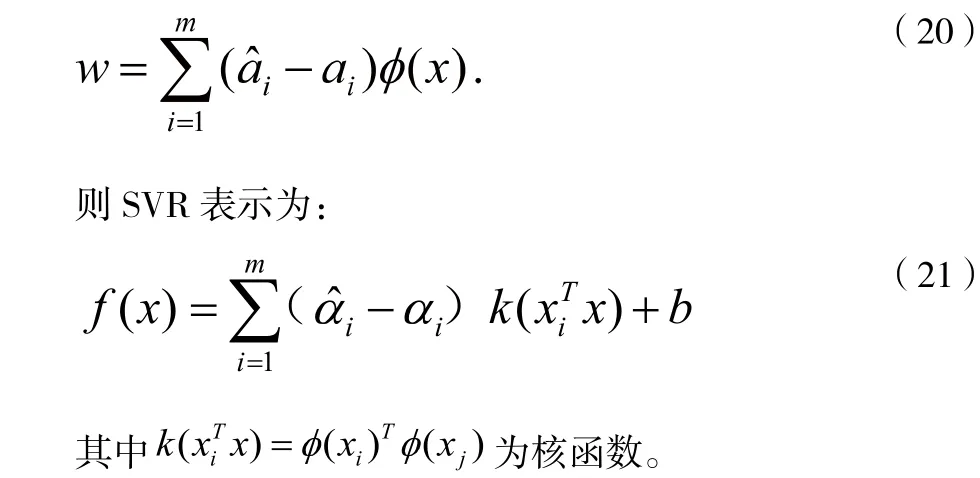



4.5 决策树,模型的建立

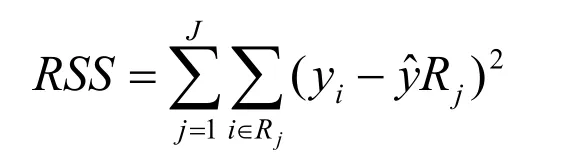



4.6 最终模型对本题的求解
5 模型的优化
