非线性连续卸荷路径下黄土的强度与变形特性研究

伏映鹏，廖红建，刘雪刚，李 瑶，张继文,2

(1.西安交通大学 人居环境与建筑工程学院，西安 710049; 2.机械工业勘察设计研究院有限公司，西安 710043)

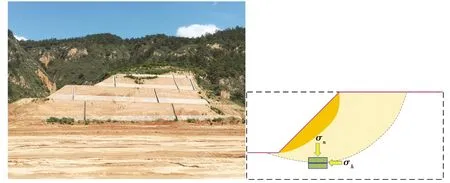
图1 某挖方边坡及垂直剖面内部一点应力状态

实际挖方工程的应力路径非常复杂，关于卸荷路径对试样力学特性的影响，相关学者采用简化的方法进行研究。如庄心善等[9]采用真三轴仪进行了不排水侧向卸荷试验，发现侧向卸荷情况下土体在较小的应变下发生破坏；张孟喜[10]对不同卸荷应力路径下的土体变形及强度特性进行了研究，发现侧向卸载的试样，其体积变形表现为剪缩性，侧向加载试样，其体积变形表现为剪胀性；张玉[11-12]进行平面应变条件原状黄土侧向卸载试验，试验表明侧向卸载条件下土的破坏应变要比平面应变竖向加载和常规三轴试验小得多；李加贵等[13]建立了侧向卸载过程细观结构演化方程；程相华[14]利用直剪仪对卸荷土体强度特性进行了研究，其发现瞬时卸载快剪强度受卸荷比、先期固结压力等因素的影响；赵春风[15]采用大型直剪试验，分析不同加、卸荷状态下接触面的力学特性，以及卸荷程度、粗糙度等对接触面软化特性和剪胀(缩)性的影响；张伏光[7]针对基坑开挖影响范围内土体的应力路径进行平面应变试验离散元模拟，发现不同卸荷应力路径卸荷土体性质差别较大且与结构性有关。此外Ng[16]和Li[17]等也研究了卸荷过程中的应力路径变化。但以上研究主要以基坑开挖涉及到的侧向卸荷为主，研究手段以常规三轴试验居多，而挖方工程更多涉及的是竖向卸荷，其不同于研究基坑开挖侧向土体的强度与变形。因此，以大规模挖填方工程挖方边坡为背景研究竖向卸荷状态下黄土的强度特性对挖方区边坡失稳机理研究具有重要的理论意义。

综合文献[7-18]可知加荷、卸荷应力路径下土体的强度与变形特性有着显著差异。从工程应用角度出发，根据挖方作业进程将竖向卸荷分为分阶段卸荷和非线性连续卸荷，基于伯努利方程对现有直剪仪进行改造，即利用带水龙头的水箱代替砝码进行加、卸载，模拟一次连续非线性挖方作业过程，以达到研究非线性连续卸荷路径下黄土强度特性的目的。

1 试样制备、试验设备及试验方法

1.1 试样制备

本试验所用黄土取自陕西省西安市曲江某基坑，土样粒径级配曲线如图2所示。

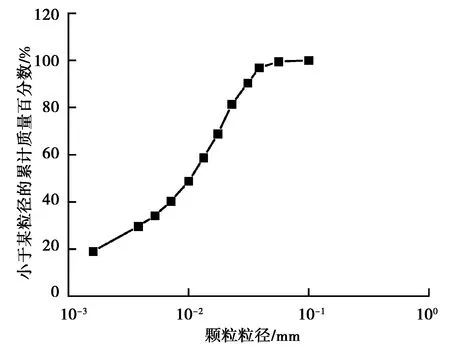
图2 土样粒径级配曲线

根据《土工试验方法标准》测定土样的物理参数，结果如表1所示。

表1 土样物理性质指标

1.2 试验设备改进思路

本次试验在应变控制式直剪仪的基础上进行改进，选择卸荷方式为水流连续卸荷，以达到非线性卸荷目的。但为了试验结果的可分析性，须考虑卸荷时间步长一致，且每一卸荷步长卸荷速率应尽量保证匀速，因此基于流体力学理论中的守恒原理设计水箱尺寸。设水箱底面积为S1，开口面积为S2。记水面下降速度为v1，水流流出速度为v2，水面高度为h1，水箱开口高度为h2，取孔口局部阻力系数ζ=0.5。水面及开口处压强相等，均为大气压p0。建立如图3所示的连续卸荷水流示意图。

图3 水流示意图

如图3所示，A和B分别为水面和水龙头处的2点，则AB为一条流线。根据伯努利方程，在AB2点有

(1)

由于水面上A点和水龙头处B点都和大气接触，所以其压强都等于大气压p0，且由式(1)可知水面和孔口的相对高度差y为

(2)

又根据连续方程有

v1S1=v2S2。

(3)

联立式(2)、(3)有

(4)

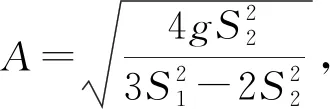
(5)

由前所述，非线性连续卸荷试验要求卸荷过程中，一个时步内尽量满足水流速度均匀和水流量均匀变化，即一个时步内尽量控制速度v1不变。由公式(5)可知，卸荷时y不断变化，要使v1的变化最小，应该控制A的值尽可能小。因此，设计的水箱应具备底面积大，开口面积小的特征。根据原有直剪装置的尺寸，设定水箱尺寸为400 mm×200 mm×200 mm，水龙头直径为20 mm，带入式(4)可得最大流速为6.36 mm/s。

室内直剪仪的砝码质量对应于作用在土样的法向压力，如要对试样施加400 kPa的法向压力，需要在杠杆端部安装10.20 kg的砝码。当改用水箱加载时，水箱总质量达到10.20 kg，同样能够对土样施加400 kPa的法向压力。因此只需称量对应于200 kPa，300 kPa，400 kPa法向压力的砝码质量，再在水箱内装好水，使水箱总质量与测得的砝码质量相同，并依次在水箱上对水位线进行标注。

由式(5)可知，卸荷过程流速不恒定，导致法向荷载非线性变化，因而可实现竖向非线性连续卸荷路径，打开不同开关(开口数)也可模拟实际工程中不同的卸荷速率。为了试验数据的可分析性，需要计算在卸荷过程中，法向荷载及卸荷比随时间的变化关系。

dt时间内卸荷比的增量dR根据定义[15,19]可写为

(6)

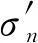
(7)

(8)

式中：α为砝码所代表的载荷量与用水质量之间的换算系数；h0为初始水面高度；Δt为卸荷时间步长；B为与水箱尺寸及出口断面有关的一个参数(B=AS1/S2)；t0为卸荷总时长。

1.3 试验方案及方法

不论是连续卸荷还是分阶段卸荷，由于土体侧向土压力系数基本稳定，侧向土压力/围压也会同时降低，由于采用直剪仪进行试验，暂不考虑侧向土压力(围压)的影响。为了对比分析设计未卸荷、非线性连续卸荷两种工况，具体试验方案见表2，不同法向荷载对应的水箱加水量见表3，其中水箱自身重量为1.35 kg。限于篇幅，主要讨论竖向非线性连续卸荷。

表2 竖向连续卸荷试验条件

表3 不同法向荷载对应的水箱加水量

试验采用固结快剪试验，即先使土样在某一法向压力作用下充分固结，再在不排水条件下打开水龙头边卸荷边剪切，剪切速率为0.8 mm/min。

2.1 卸荷时间与卸荷比的关系

通过水箱尺寸计算得到S2，B，通过表3可得到初始水面高度h0，水的密度ρ，换算系数α，将其带入式(7)、(8)并考虑等效开口面积，可计算得到连续卸荷过程中卸荷时间与卸荷比的关系曲线，如图4所示。

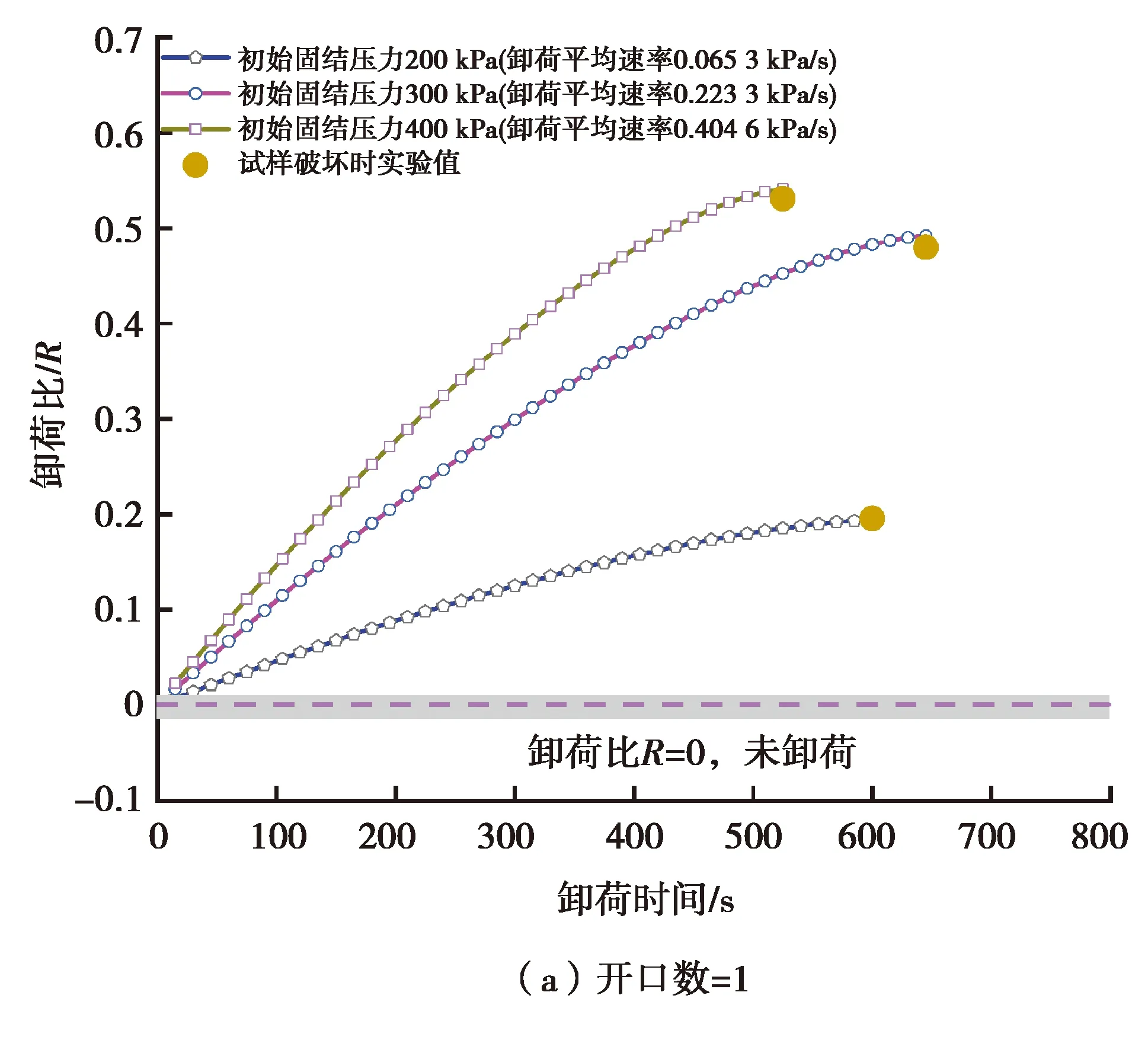
图4 不同固结法向荷载R-t关系

由图4可知，卸荷比R与时间t表现出非线性关系，即连续卸荷过程中，法向荷载随卸荷时间的增加趋于稳定；固结法向荷载σn越大，单位时间内剪切法向荷载的变化量越大；当试样达到破坏时，试验得到的卸荷比与理论计算比较接近，当开口数=1且初始固结压力为200 kPa,300 kPa,400 kPa时理论计算与试验结果误差分别为0.8%，2.46%及1.8%，开口数=2时，误差分别为0.28%，0.049%以及0.094%，说明卸荷比的理论推导结果是可信的。进一步据剪切速率可计算得到卸荷过程中剪切位移与卸荷比之间的关系，其对分析非线性连续卸荷强度至关重要。

2.2 剪应力与剪切位移关系分析

2.2.1 卸荷速率对剪应力与剪切位移影响

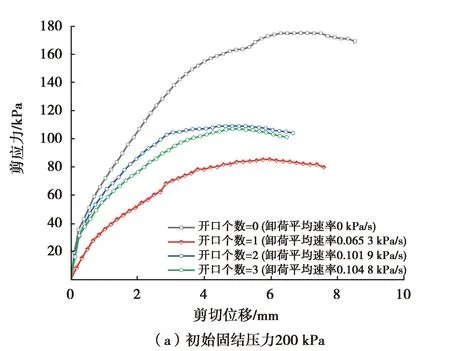
图5 不同卸荷速率下试样剪应力-剪切位移关系

庄心善[9]通过研究发现基坑开挖的侧向卸荷使土体抗剪强度降低，抵抗变形的能力减小；张玉[11-12]等人同样得出侧向卸荷侧向应变的发展要快于竖向应变。而由图6可知，与未卸荷工况相比，竖向非线性卸荷条件下土体剪应力达到峰值强度时的剪切位移明显减小，且竖向固结压力越大，峰值剪切位移的降低程度越大，这表明在竖向卸荷条件下土样同样容易在小变形时发生剪切破坏。

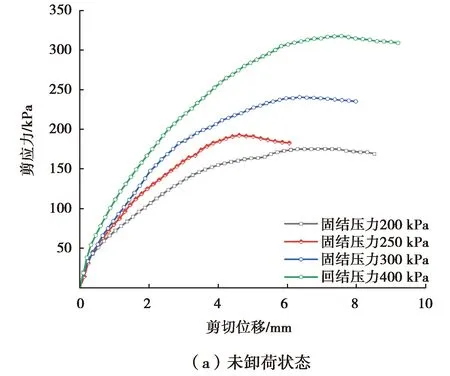
图6 不同初始固结压力下试样剪应力剪切位移关系

3 强度特性分析

图7 不同试验方案总应力路径

由图7可知，对于非线性连续卸荷，当初始固结压力为200 kPa和300 kPa时，其峰值剪应力在未卸荷强度包线之下，但随着初始固结压力增加至400 kPa，初始固结压力对强度的影响开始显现，说明非线性连续卸荷条件下，抗剪强度与初始固结压力有关，随着初始固结压力的增加，超固结效应增强，张俏楚[23]通过研究同样发现了基坑开挖侧向卸荷过程中诱发的土体超固结效应随深度的增加而降低。

本试样为黄土状粉质黏土，其抗剪强度参数由黏聚力与内摩擦角2部分构成，考虑到岩土材料黏聚力和内摩擦的构成及岩土材料发挥出的抵抗变形的能力随外荷载变化而变化，可推断岩土材料表现出的黏聚力和内摩擦是变化的，峰值强度参数是变形过程某一时刻岩土材料的强度特性。目前已有许多学者[24-28]应用黏聚力和内摩擦角随变形发展模型来研究岩土材料的强度和变形。由于卸荷对试样强度产生了明显的影响，为了更好地分析卸荷对强度参数的影响，定量地探讨卸荷比对黏聚力和内摩擦角的影响。

采用Mohr-Coulumb准则描述土体的强度演化特性，卸荷前满足

τ=σntanφ+c，

(9)

卸荷后

(10)

未卸荷工况下，随着剪切位移的增加，试样的黏聚力和内摩擦角在发生变化，参考文献[24-28]，计算得到未卸荷时黏聚力与内摩擦角随位移的变化曲线，如图8所示。

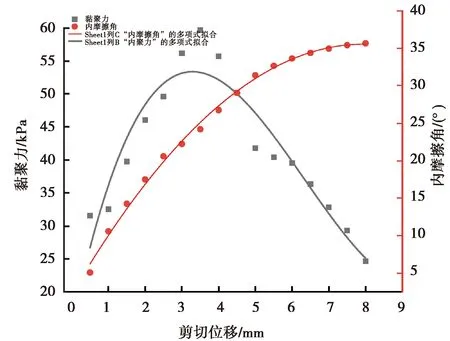
图8 未卸荷工况下强度参数与剪切位移关系

由图8可知，在变形初始阶段，抗剪强度中黏聚力所占的比重较大，随着变形的增加，黏聚力的影响逐渐降低，摩擦提供的强度开始占主导地位，这一结论与[24-28]等的研究结论均一致。

由于非线性连续卸荷试验变量的复杂性，分析过程中如果同时考虑黏聚力与内摩擦角受卸荷比的影响，就会使分析变得困难，基于未卸荷内摩擦角与黏聚力的变化规律，首先假设卸荷前后黏聚力不受卸荷比影响，结合式(9)(10)，化简后可得

(11)

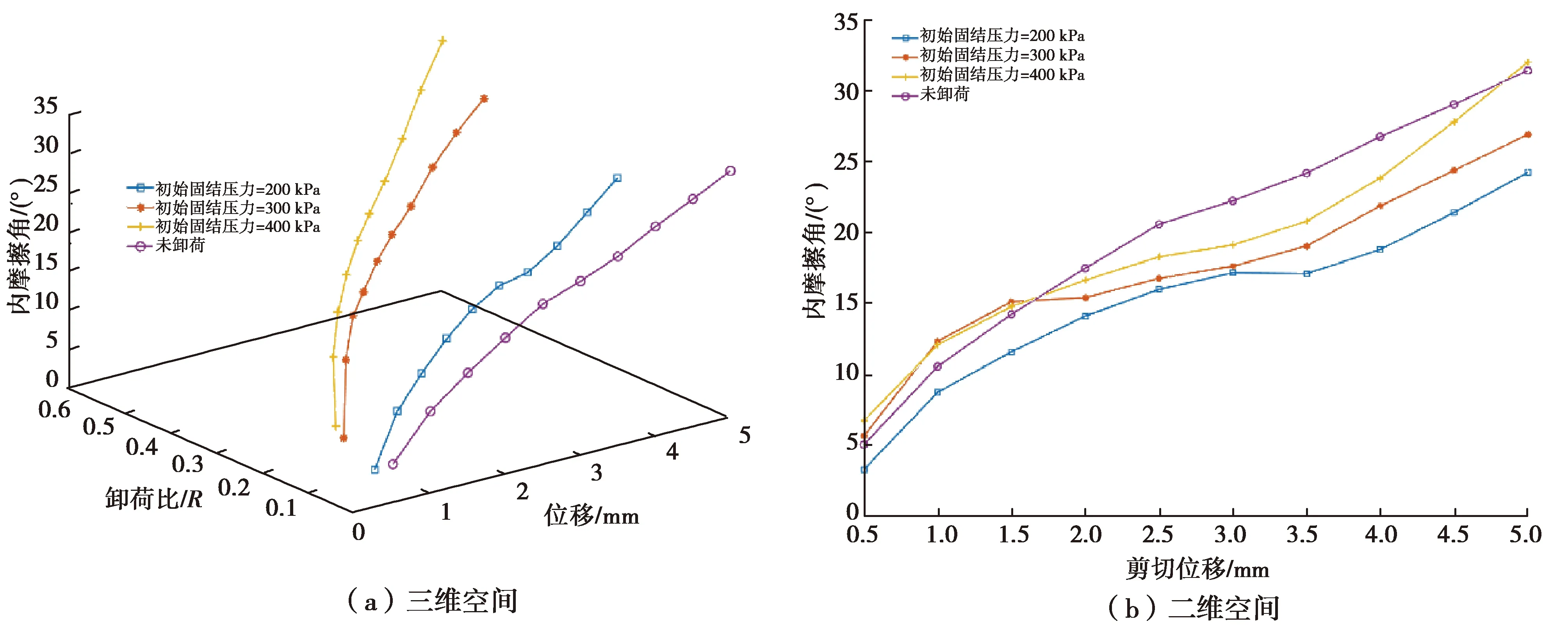
图9 非线性连续卸荷工况下内摩擦角与剪切位移及卸荷比关系

由图9可知，当假设卸荷前后黏聚力不变时，得到的内摩擦角在剪切位移小于2 mm时，大于未卸荷，这主要是由于忽略了黏聚力的影响造成的，其不符合实际。结合图8未卸荷内摩擦角、黏聚力的变化规律，并考虑图9中假设黏聚力不变得到的内摩擦角随剪切位移变化的关系，可以采用指数衰减的数学模型(式(12))描述卸荷后内摩擦角随卸荷比、位移的变化

φ″=φ″(δ,R)=φ(δ)×e-χR(δ)，

(12)

其中：χ为与初始固结压力相关的参数；φ(δ)为卸荷前内摩擦角与剪切位移的关系，将式(12)绘制于剪切位移(δ)与内摩擦角(φ)空间，如图10所示。

图10 非线性连续卸荷后黏聚力与剪切位移关系

由图10可知，当剪切位移大于2 mm时，式(12)可以很好地描述非线性连续卸荷过程中内摩擦角随剪切位移的变化规律，这主要原因是非线性连续卸荷过程中，当剪切位移>2 mm时，黏聚力较小，其对内摩擦角的变化影响较小；而当剪切位移<2 mm时，采用式(12)计算得到的结果位于未卸荷曲线下方，符合实际情况，因此采用式(12)描述非线性连续卸荷过程中内摩擦角随剪切位移的变化规律是合理的。由式(12)进一步根据Mohr-Coulumb准则，可计算得到卸荷后黏聚力随剪切位移的变化关系。

C′=τ′-(σn-R(δ)σn)tanφ″(δ)，

(13)

基于式(13)计算得到的数据，为了在形式上与卸荷后内摩擦角随卸荷比、剪切位移保持一致，同样采用如式(14)所示指数衰减的数学模型来描述卸荷后粘聚力随卸荷比、剪切位移的变化

C″=C″(δ,R)=C(δ)×λe-κR，

(14)

式中，λ和κ为与竖向固结压力有关的参数。式(13)和式(14)结果如图11所示，如图11可知，采用式(14)的形式可以较好地描述非线性连续卸荷过程中，黏聚力随剪切位移的变化关系。利用卸荷比将图10和图11横坐标变换为法向荷载，可以更直观地看到非线性连续卸荷过程中黏聚力与内摩擦角随法向荷载的变化，如图12(a)和图12(b)所示。由图12(b)可知，当初始固结压力等于400 kPa时，实验值与理论值相差较大，其主要原因是：当初始固结压力等于400 kPa，主要由内摩擦抵抗剪切变形，而黏聚力基本不随固结压力变化，在抗剪强度成分中所占比重较小，因而忽略内摩擦的影响时，误差较大；同时由12(a)可知，当忽略黏聚力时，内摩擦角与理论较为接近，也说明了当初始固结压力为400 kPa时，主要由内摩擦抵抗变形。

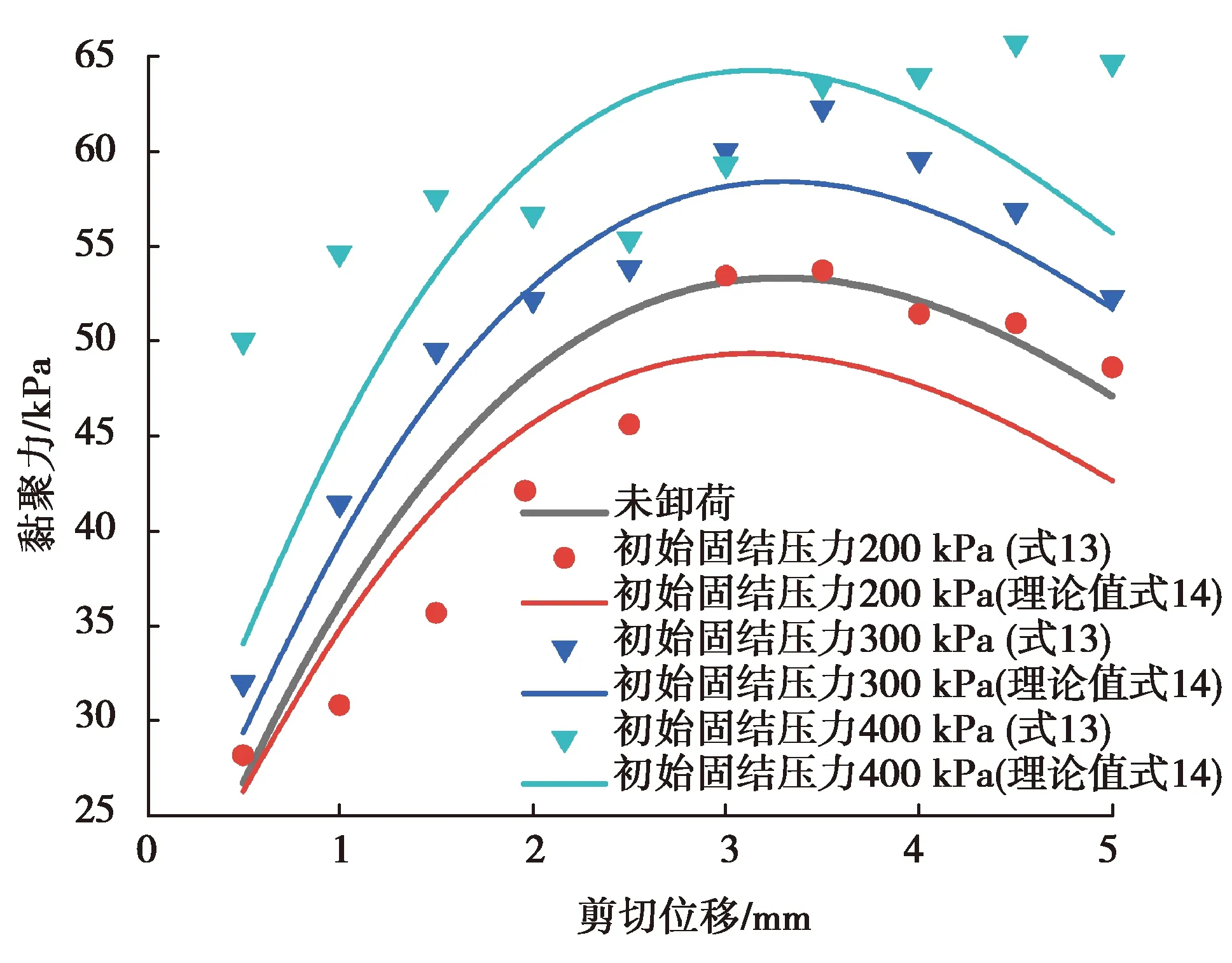
图11 非线性连续卸荷后黏聚力与剪切位移关系

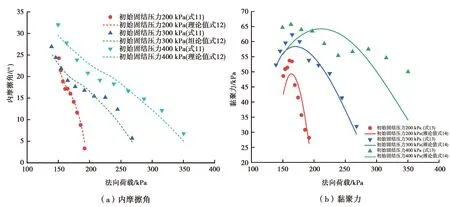
图12 非线性连续卸荷过程中竖向剪切荷载与强度参数之间的关系

4 结 论

采用水箱代替砝码实现连续卸载研究了竖向非线性连续卸荷工况下黄土的强度与变形特性，得到以下结论：

1)基于伯努利方程推导得到的卸荷比能够很好地描述试样在连续卸荷过程中法向荷载的变化。

3)非线性连续卸荷路径下，抗剪强度与初始固结压力有关，随着初始固结压力的增加，超固结效应越明显。

4)所给出的强度参数(内摩擦角和黏聚力)随剪切位移的变化模型，较好地描述了非线性连续卸荷路径下强度参数演化规律，但由于非线性连续卸荷，涉及到的变量多且难以控制，其关系式仍需进行更深一步的研究。