既有改扩建浅埋岩石隧道的围岩压力计算方法研究
2021-06-21柏谦赵文王鑫程诚路博
柏谦,赵文,王鑫,程诚,路博
(东北大学资源与土木工程学院,辽宁沈阳,110819)
随着城际高速铁路作为我国“新基建”的七大模块之一,将会进一步促进我国隧道建设的发展,考虑到隧道建设的经济成本,对既有废弃或损坏较严重的隧道进行改扩建是建设隧道的有效途径之一[1]。隧道扩建是在已有隧道断面上进行扩挖,这将导致隧道周边的围岩产生应力重分布,给施工过程带来不可预知的问题,甚至引发工程事故[2]。因此,如何预估隧道改扩建过程中受到重复扰动的围岩应力已成为目前亟待解决的问题。在改扩建隧道的支护结构设计和围岩应力分析时,如采用新建隧道的方法,可能会造成支护结构设计偏于危险,给隧道施工带来安全隐患,因此需要对传统隧道围岩压力计算方法进行改进。
国内外学者对隧道围岩应力的计算进行了一些研究。SINGH 等[3-6]提出或修正了计算围岩压力的理论或经验计算方法,其中传统太沙基围岩压力计算方法为了便于计算,将滑裂面简化为沿隧道拱顶垂直向上延伸,显然与实际情况不符;李鹏飞等[7]通过分析隧道埋深和隧道跨度等参数对围岩压力计算结果的影响,分析比较了几种围岩压力计算方法的优缺点和适用范围,其中普氏公式适用于有一定自承载能力的深埋隧道,太沙基公式适用于围岩条件较差的浅埋隧道。孙振宇等[8]基于大量现场实测数据的统计分析,推导了更符合实际的小净距隧道围岩压力表达式。肖明清等[9]通过分析经典修正惯用法在复合地层围岩压力计算中存在的问题,基于极限状态理论范畴的滑移线理论推导出了复合土层下部主动土压力的计算公式。邱业建等[10-12]提出了隧道围岩压力的上限解计算方法。然而,这些隧道围岩压力计算方法中的假设条件均具有一定的局限性。伍冬[13]认为作用在隧道结构上部的竖向压力为隧道上部土体的自重,忽略了滑动面上的摩阻力,因而计算结果偏大。比尔鲍曼公式、谢家杰公式虽然考虑了土体的拱效应,但这些公式的计算结果相差较大[14]。
鉴于此,本文作者结合既有南岭隧道改扩建工程,首先根据扩建隧道的地层沉降曲线确定滑裂面的位置,并将拱顶上方的滑裂面曲线简化为倾斜的直线,然后考虑土体两侧重力及滑裂面与土体间的摩擦力,从应力传递角度出发求解出扩建隧道的围岩压力,提出隧道改扩建围岩压力的计算公式,并结合工程案例验证了提出公式的正确性和合理性。
1 工程概况
本文依托工程为既有南岭隧道扩建工程,南岭隧道建于1924年,位于辽宁省北票市上园镇、大板镇交界处,总体呈近东南至西北向展布,隧道全长1 187.10 m,纵坡6‰,属浅埋拱形隧道,最大埋深37.75 m,围岩等级以IV 级和V 级为主。隧道进口位于北票市上园镇土家营村南岭站北侧山坡上,地表覆盖杂草和灌木及农田;出口北票市大板镇黄土坎村梨树沟组东面山坡上,坡度较陡,碎石裸露,地表土覆盖很薄,植被为杂草和灌木为主。图1所示为隧道内部衬砌图。由图1可见:既有南岭隧道局部限界不足较严重,衬砌开裂、错动、腐蚀现象严重,漏水现象较严重,因此既有南岭隧道需扩挖换衬砌后才能满足电气化铁路隧道限界条件。
南岭隧道的断面如图2所示。初始隧道宽度为5.5 m,高度为8.1 m,高跨比为1.47,断面面积为41.3 m2。扩挖后宽度为7.15 m,高度为9.25 m,高跨比为1.29,断面面积为64.9 m2。
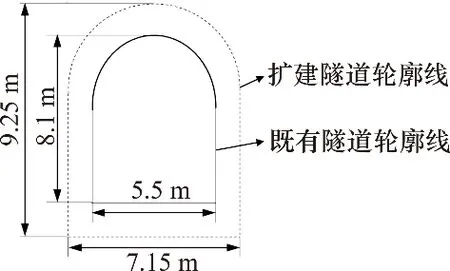
图2 南岭隧道截面图Fig.2 Section diagram of Nanling tunnel
2 隧道围岩破坏滑裂面位置的确定
隧道塌方是围岩破坏导致的最常见形式之一,大量的工程实例和试验均表明,当地质条件较差或支护不及时,隧道开挖后由于卸荷作用将导致隧道周边围岩产生较大的变形,拱顶首先出现塌落,随后形成贯通至地表的滑移破坏[15-17]。地表沉降曲线中竖向位移变化率最大的点为反弯点,本文假设反弯点为滑裂面所在位置[18],利用Midas GTS 建立有限元模型计算并找到各平面内的反弯点,然后结合最小二乘法求解其曲线形式,即得到整个隧道的滑裂面曲线,进而确定滑裂面位置。
2.1 计算模型建立
本文选取依托工程V 级围岩埋深最大段建立计算模型,如图3所示。
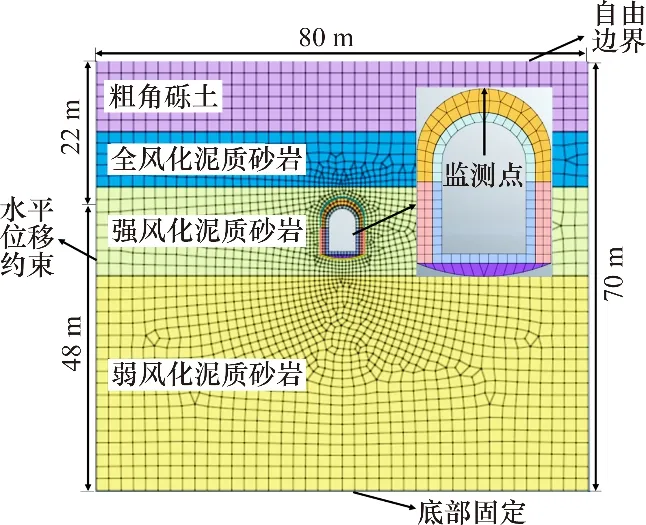
图3 计算模型图Fig.3 Diagram of calculation model
模型横向长度取80 m,竖向取70 m,隧道埋深为22 m。上部取至地表,隧道两侧及底部距模型边界长度均为洞径的3~5倍。上部地表为自由边界不设约束,下部固定,四周为水平位移约束。土体和既有隧道衬砌采用平面应变单元,扩挖隧道初期支护及二衬采用梁单元,锚杆采用植入式桁架单元。土体本构采用摩尔库仑强度准则,既有隧道衬砌、初期支护、二衬及锚杆采用弹性本构。初始应力场按自重应力场模拟,依据现场施工工况,分为8个施工阶段,用S1~S8表示,分别为初始应力状态模拟、既有隧道上台阶衬砌拆除及扩挖、上台阶初期支护、既有隧道下台阶衬砌拆除及扩挖、下台阶初期支护、仰拱开挖、仰拱支护和扩建隧道二衬。隧道扩挖步的荷载释放系数设为0.6和0.4,施工过程采用台阶法开挖,不考虑超前支护对施工过程的影响。模型共有2 688个单元,2 761个节点。围岩计算参数见表1。
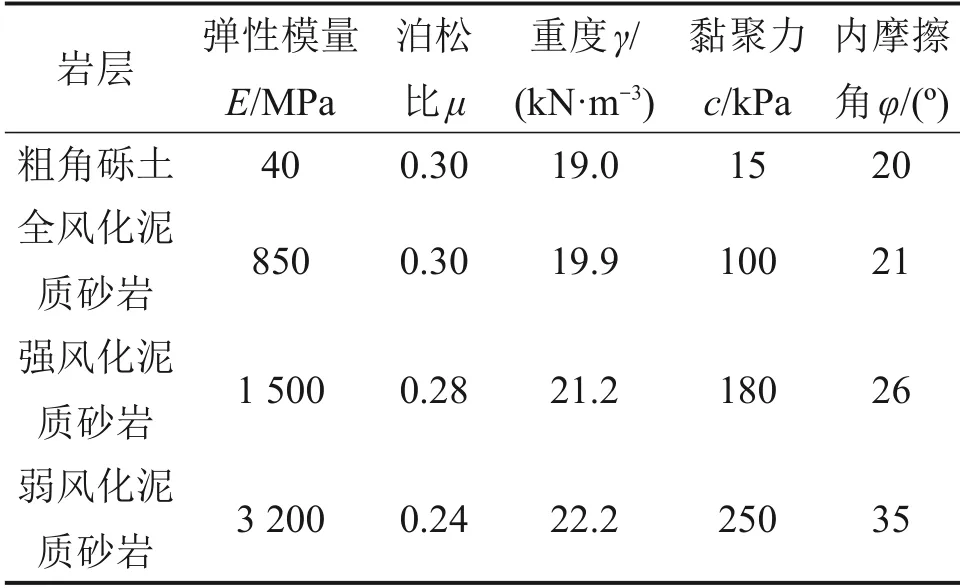
表1 V级围岩物理力学参数Table 1 Physical and mechanical parameters of surrounding rock of V grade
由于隧道修建年限较长,隧道漏水现象较严重,原始初期支护及锚杆均受到不同程度的腐蚀、锈蚀,且原始初期支护在隧道扩挖过程中对围岩稳定性影响较小。因此,隧道扩建数值模拟过程中忽略原始初期支护的作用,仅考虑隧道原始二衬及原始锚杆的作用,并将隧道原始二衬及原始锚杆弹性模量按照日本隧道规范[19]和王文正[20]的建议折减20%。
数值模拟中,采用等效弹性模量的方法[21]模拟砂浆锚杆,等效弹性模量按下式计算:

式中:E1和A1分别为锚杆的弹性模量和截面面积;E2和A2分别为砂浆体的弹性模量和截面面积;EBE为锚杆等效体的弹性模量。
扩挖隧道初期支护中格栅钢架同样采用等效法[22]来模拟,根据抗压刚度相等的原则,将格栅钢架的弹性模量折算为喷射混凝土的弹性模量,计算公式为:

式中:ESE为折算后喷射混凝土弹性模量;E0为原喷射混凝土弹性模量;Eg为钢架弹性模量;Ag为格栅钢架截面面积;Ac为喷射混凝土截面面积。
扩建隧道支护结构最终计算参数如表2所示。
2.2 计算模型验证及结果分析
隧道拱顶沉降在初期支护面布设全站仪测点反光片,利用全站仪进行观测,每天观测1次,观测周期为16 d。数值模拟隧道拱顶沉降监测点与现场观测点一致,将拱顶沉降数值模型计算结果与现场监测数据进行对比,对比结果如图4所示,施工阶段S1~S8 与现场监测周期相对应。由图4可知:本文建立的数值模型拱顶沉降计算结果与现场实测拱顶沉降规律相同,且数值模拟拱顶沉降最大值与监测数据相差仅0.3 mm,表明本文通过数值模型确定的滑裂面位置具有一定的参考性。

图4 数值模型与监测数据对比Fig.4 Comparison between numerical model and monitoring data
利用Midas GTS软件提取数值模型中隧道上方各地层平面的竖向位移,通过各地层平面的沉降曲线找出反弯点,进而得出围岩的滑裂面曲线。因地层平面数较多,本文只提取其中4个平面,分别距地表0,5.75,11.5和16.9 m,4个平面的沉降曲线见图5,其中y为距地表的竖向距离。由图5可知,4 个平面的沉降曲线都存在2 个对称的反弯点。

图5 部分平面沉降曲线图Fig.5 Partial plane settlement curves
采用同样的方式找到各地层平面沉降曲线上的反弯点,然后通过最小二乘法对反弯点进行曲线拟合,得到整个隧道的滑裂面曲线,依托工程反弯点坐标及拟合滑裂面曲线如图6所示。由图6可以看出,依托工程滑裂面曲线符合王志伟等[6]研究得到的乘幂函数形态。

图6 反弯点拟合曲线图Fig.6 Curve fitting of inflection point
对依托扩建隧道工程建模计算分析,得到了适用于浅埋隧道的滑裂面曲线的确定方法,如图7所示,其中,x为距隧道中轴线的水平距离。
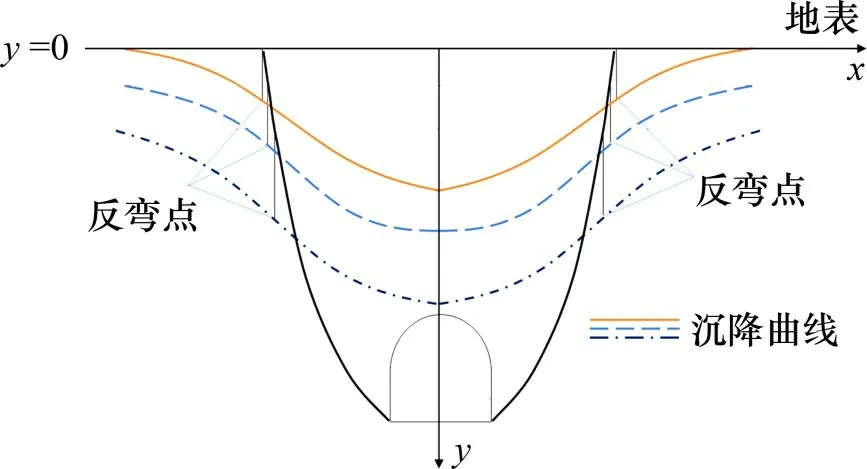
图7 滑裂面确定方法示意图Fig.7 Schematic diagram of determination method of slip surface
3 隧道围岩压力计算公式的推导
隧道滑裂面一般为乘幂函数曲线,然而当进行围岩压力计算时,曲线滑动面将会导致计算十分繁琐,因此首先将曲线滑动面进行简化。由隧道滑裂面曲线可以看出,距离隧道较近时,滑裂面曲率变化较大,随着距地表的距离逐渐减小,滑裂面曲率变化率逐渐减小,基本趋于一条直线。因此,本文首先将隧道拱顶以上部分滑裂面简化为一条倾斜的直线,这样不仅可以保证一定的计算精度,而且可以简化计算过程,如图8所示,其中,H为隧道拱顶到地表的竖向距离,H1为隧道高度,2a为隧道宽度,2b为隧道两侧滑裂面曲线的水平距离,X为隧道拱顶距滑裂面曲线的水平距离。推导出在滑裂面曲线为直线情况下的围岩压力计算公式后,再将乘幂函数代入该公式,进而得出符合实际情况的围岩压力计算公式。

图8 围岩压力计算图Fig.8 Calculation diagram of surrounding rock pressure
由图8可见:直线AB的斜率为曲线滑裂面在拱顶平面位置处的导数。在上部岩体中切取厚度为dh的薄层单元,并对1/2薄层单元进行单元受力分析,薄层受到上部竖向荷载σv、下部竖向荷载σv+dσv、岩体重力W、侧面的支撑力R及侧面摩阻力τ1和τ2共5 种作用力,计算模型如图9所示,图中,σh为水平侧向荷载。

图9 1/2薄层单元受力图Fig.9 Force diagram of 1/2 thin layer unit
由该部分岩体的水平方向受力平衡可得:

式中:σh=kσv;τ2=Rtanφ+c;k为侧压力系数。
由式(3)可得:

整个薄层单元受力分析如图10所示。

图10 薄层单元受力图Fig.10 Force diagram of thin layer unit
由竖向受力平衡∑V=0可得:

整理式(5),并略去二阶微量得:
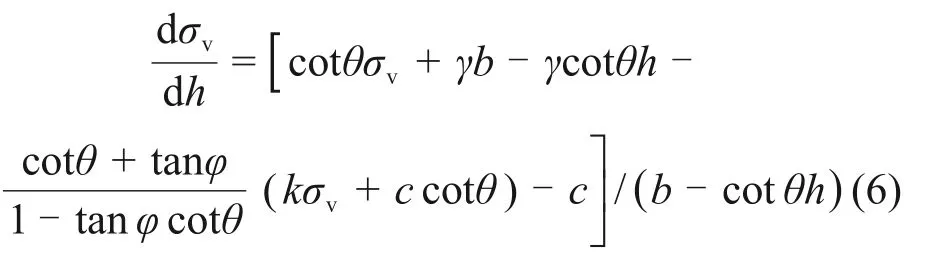
令m=cotθ,式(6)可转化为

利用Matlab 进行求解,并引进边界条件(h=0,σv=0),可得:

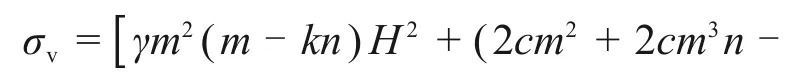
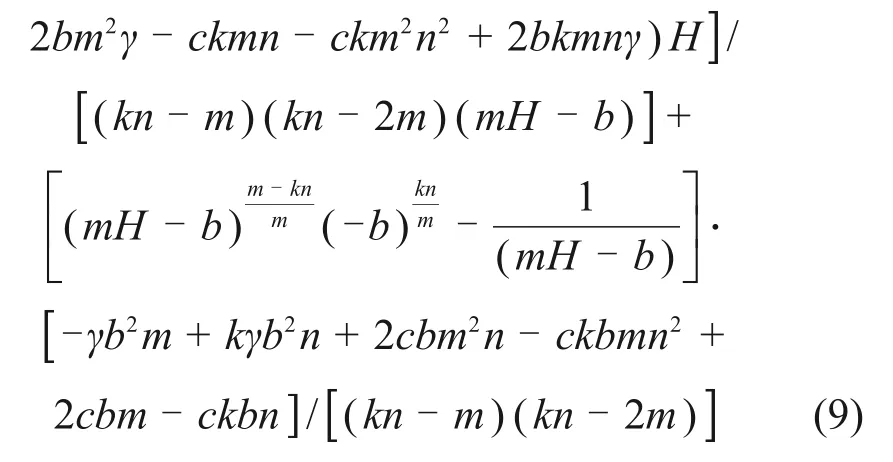
则隧道顶部压力e1和底部压力e2分别为:

若为均布压力,则:

4 工程实例分析
为了验证本文提出围岩应力计算公式的正确性,将计算值与依托工程围岩压力数值解进行对比,并另外选取2个不同浅埋隧道工程案例的围岩压力监测断面进行验证,工况一[21]为外径10 m,内径约8 m,覆土厚度约10 m,跨度10 m,埋深14 m 的隧道;工况二[23]为直径6.2 m,覆土厚度6.72 m,跨度6.2 m,埋深约12 m 的隧道。2 个工况隧道断面计算参数取值如表3所示。

表3 工程实例计算参数取值Table 3 Calculation parameter of examples
采用本文方法和太沙基公式分别对依托工程及上述2个工况的围岩压力进行计算,侧压力系数k根据太沙基试验结果取为1.0[24],计算结果如图11所示。
由图11可以看出:在工况一条件下,采用本文提出的计算公式和太沙基公式得出的计算结果与实测值分别为212.8,219.8 和206.6 kPa,2 种计算方法与实测值的相对误差分别约为3.00%和6.39%;在工况二条件下,2 种计算方法与实测值的相对误差分别约为0.25%和6.03%;在依托工程条件下,本文计算结果、太沙基公式计算结果与数值解相对误差分别约为1.04%和9.16%。由此可见,采用本文方法计算得出的围岩压力略小于太沙基公式的计算结果,与实测值更加接近,且在工况二和依托工程条件下本文计算方法得出的围岩压力与实测值趋于重合,验证了本文提出的围岩压力推导方法的合理性和普适性。
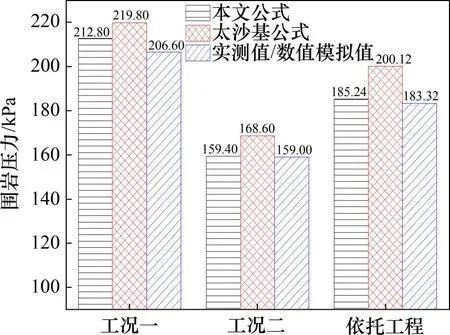
图11 围岩压力对比Fig.11 Comparison of surrounding rock pressure
5 结论
1)确定了地层各平面沉降曲线中的反弯点为滑裂面所在位置,给出了扩建隧道围岩滑裂面确定方法。
2)基于传统太沙基理论,从应力传递角度出发推导了改扩建浅埋隧道围岩压力的计算公式。
3)考虑滑裂面左右两侧的岩体重力和倾斜破裂面上岩体的摩擦力改进了围岩压力计算方法,计算结果与实测值最大相对误差不超过3%,验证了本文所提计算方法的准确性。
