基于贪婪策略的低复杂度功率分配算法
2021-06-21袁伟娜王艳龙刘伟婷郭逸飞王硕恒
袁伟娜, 王艳龙, 刘伟婷, 郭逸飞, 王硕恒
(华东理工大学信息科学与工程学院,上海 200237)
移动用户数的爆炸式增长使得5G将会面临海量用户的接入[1-2],而传统的多址接入技术已无法满足更高的容量要求,因此急需改进现有的多址接入技术,由此,日本DoCoMo公司提出了功率域非正交多址接入 (Non-Orthogonal Multiple Access,NOMA)[3]技术。
NOMA的基本思想是在发送端发送叠加信号主动引入干扰信息,然后在接收端根据串行干扰消除技术进行解调[4-6]。因而如何在发送端进行功率分配,对提高系统的吞吐量和降低用户间多址干扰有很大的影响[7]。
根据文献[8]的总结,目前对NOMA系统性能的关注主要集中在能量效率(EE)、用户公平性(MMF)、系统吞吐量(SF)这3个方面。文献[9]提出了提高NOMA系统能量效率的功率分配算法;文献[10-11]详细研究了最大化用户间公平性的功率分配算法;文献[12]提出的全空间搜索的功率分配(Full Search Power Allocation,FSPA)算法采用枚举法计算出各种功率分配情况下的吞吐量,可使总吞吐量达到理论上的最优值,但由于较高的计算复杂度,实用性较差。文献[13]提出了具有较低复杂度的固定功率分配 (Fixed Power Allocation,FPA) 算法及分数阶功率分配 (Fractional Transmit Power Allocation, FTPA) 算法,但FPA没有考虑实际的信道质量,吞吐量性能较差;FTPA考虑了信道质量及路径损耗等问题,但由于功率分配方式简单,算法的性能仍有待提高。目前的研究工作主要集中在保证服务质量(QoS)以及给不同用户分配不同权值这两种方向。文献[14]基于这样的思路,提出了一种吞吐量接近理论最优值、且具有较低复杂度的功率分配算法。
本文根据SIC接收机的特点及用户间的功率关系,提出了一种新的基于贪婪策略的功率分配算法。首先对用户进行排序及动态分组,然后进行局部吞吐量最优判断,并留下每组中的最优情况,其余的进行删除处理。该算法成功地将FSPA算法的复杂度从随用户数指数级的增长降低到线性级的增长,并且保证了吞吐量性能基本相同。最后通过仿真对比分析了上述几种主要算法的吞吐量性能,从而验证了本文算法的优势所在。
1 NOMA系统
本文中子信道之间仍采用正交频分多址(Orthogonal Frequency Division Multiple Access,OFDMA)技术[15-16],而一个子信道由多个用户共享。图1示出了NOMA系统频带资源分布,其中N为单个子信道上同时复用的用户数,βmn为用户的功率分配系数。设各子信道分配的总功率相等,则单个子信道的总功率pk=pBS/m,其中pBS为基站发射总功率,m为子信道数。由于经OFDMA技术可滤除其他子信道干扰,所以本文主要研究单个子信道内下行链路的功率分配问题。

图1 NOMA系统频带资源分布Fig. 1 Frequency band of NOMA
图2示出了一个基站两用户下行链路NOMA系统模型。系统为单发射、单接收天线,两用户需要发射的信号分别为x1,x2, 发射功率为pi,则叠加信号为


图2 两用户下行链路NOMA系统模型Fig. 2 Downlink NOMA system model for two users

根据香农定理,可得两用户的吞吐量分别为
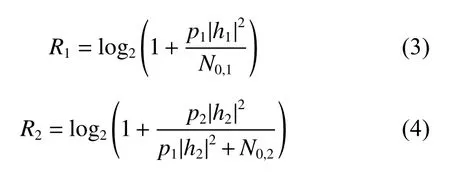
实际系统中,一个子信道上肯定不止两用户在复用,为不失一般性,假设用户数为N,根据信噪比(SINR)大小降序排列后的用户数组可表示为{UE1,UE2,···,UEN},则用户n的接收信号为

式中:hn为用户n的信道增益;xk为用户k的传输信号;pk为其分配的功率;In为小区间干扰;nn为高斯白噪声。考虑到小区远近效应的影响,小区边缘用户由于信噪比较低会被分配更大的功率,所以式(5)改写为

经过SIC接收机处理后,用户n的信噪比可表示为
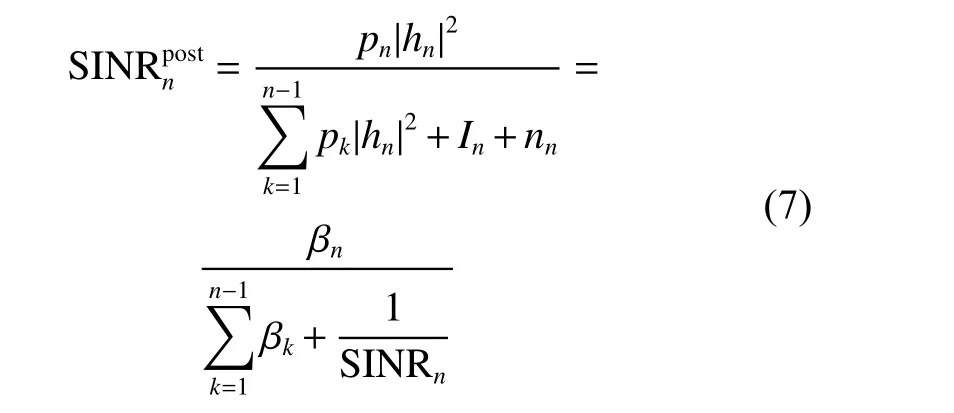
根据香农定理可以得出吞吐量:


2 基于贪婪策略的功率分配算法
2.1 功率分配算法原理

由式(8)可知,对于用户n,无论前面的n−1个用户的分配情况怎么变化,只要当前状态确定,局部的吞吐量就确定,且更下层用户的分配情况也不会影响当前的吞吐量性能,即本文的贪婪策略满足无后效性,最终解是全局最优的。具体的处理过程可以用一种数据结构中典型的树结构来体现,如图3所示。式中:∆为最小间隔。



图3 本文算法树状结构图Fig. 3 Tree structure of this paper
算法步骤如下:
(3)局部最优判断,删除多余分支。首先对与用户n相连的下一层的Snk计算其功率分配系数和:Ωn=Ωn−1+βn,其中 Ωn−1为上一层和节点的功率分配系数之和。接下来把 Ωn相同的路径分配到同一组,如结构图中所示汇集到同一个Sn点。然后根据计算式Tn=Tn−1+Rn对每组中所有的功率分配组合进行吞吐量计算,其中Tn−1为上层连至根节点的所有用户吞吐量之和,Rn根据式(8)进行计算。同一组的分支中,最终只留下可使吞吐量达到最大的一个分支,其余分支做删除处理。这样使得每层的和节点都与其上一层的某个和节点有且仅有一条幸存支路相连,保证了树结构的正确性。
(4)最后一层处理及输出最优路径。最后一层只有一个分组即 ΩN=1 ,且每个节点下只有一个分支 βN=1−ΩN−1, 经判断,留下使最终的吞吐量TN达到最大的分支。根据这个唯一的分支,自下向上遍历至根节点,输出使总吞吐量达到最大的全局最优的功率分配组合 { β1,β2,···,βN} 。


2.2 复杂度计算及分析
本文算法的时间频度T(n) 为需要搜索的功率分配组合的数量,即整个树状结构所需处理的总分支数,求解过程如下:

3 仿真分析
3.1 仿真参数选取
将本文算法与文献[14]算法进行了仿真分析比较。为使仿真结果更接近实际情况,仿真参数主要选自LTE规范[18-20],见表1。
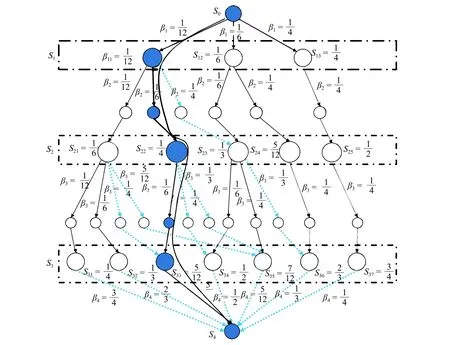
图4 4个用户的树结构图Fig. 4 Tree structure of 4 users

表1 主要的仿真参数Table 1 Simulation parameters
3.2 仿真结果及分析

图6示出了FSPA算法与本文算法的吞吐量对比结果。用3种散点值分别代表FSPA算法的3种吞吐量,用3种线型来代表本文算法的3种吞吐量。从仿真结果不难发现,点线之间接近拟合,说明本文算法在3种吞吐量性能评估上都非常接近于FSPA算法,也间接地验证了被舍弃删除的支路的确是局部吞吐量性能更差的组合。本文算法的小区边缘用户的吞吐量更大,是因为考虑了用户间的公平性,保证了小区边缘用户在同时复用的所有用户中有着最大的功率分配因子。
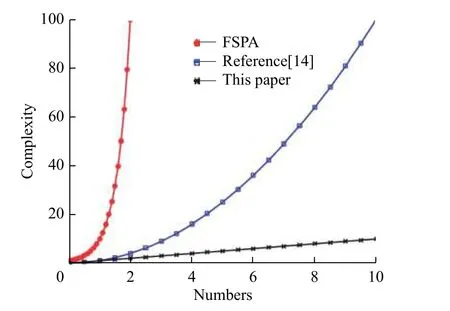
图5 3种算法复杂度对比Fig. 5 Complexity comparison of three algorithms

图6 FSPA与本文算法的吞吐量对比Fig. 6 Throughout comparison between FSPA and this paper
3.2.2 系统吞吐量的对比仿真 图7、图8、图9分别示出了文献[14]算法、本文算法、FTPA算法、FPA算法在系统总吞吐量、几何平均吞吐量、小区边缘用户吞吐量上的对比结果。其中FTPA算法和FPA算法的固定系数分别取使其能达到最优解的0.7和0.1[13]。
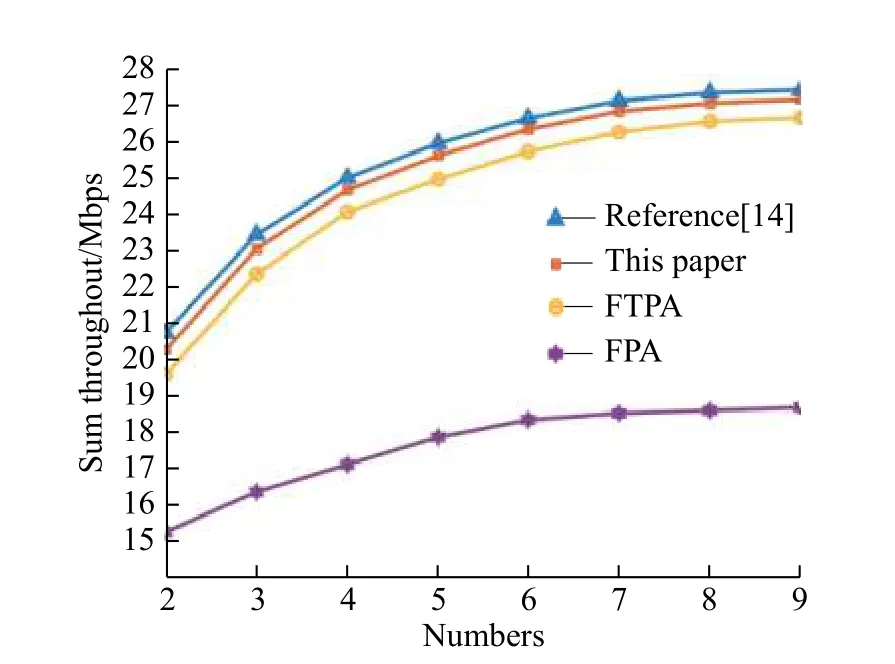
图7 4种算法总吞吐量对比Fig. 7 Overall cell throughout of four algorithms

图8 4种算法几何平均吞吐量对比Fig. 8 Geometric cell throughout of four algorithms

图9 4种算法小区边缘用户吞吐量对比Fig. 9 Cell-edge user throughout of four algorithms
可以看出,在3种吞吐量的性能对比上,FPA算法与其他3种算法的差距较大,这与其自身较简单的功率分配策略有关。本文算法和文献[14]算法的各种吞吐量性能基本一致,非常接近理论最优值且都明显优于FTPA算法。与文献[14]算法平方级的复杂度相比,本文算法的线性级复杂度明显具有更大的优势。
从图8、图9中可以看出,无论是采用哪种功率分配算法,几何平均吞吐量及小区边缘用户吞吐量随着同时复用的用户数的增加,都会不可避免地逐渐减小,最终趋于平稳。这主要是因为系统本身的时频资源有限,且根据式(8)可知用户间的干扰也会逐渐增加,导致信噪比随之下降,以致每个用户的吞吐量最终都会下降。
4 结 论
本文根据SIC的检测原理及贪心算法中局部最优判别的思想,提出了一种新的低复杂度功率分配算法,并用树的结构呈现出了这种思想。仿真分析发现,在和全空间搜索功率分配算法的总吞吐量非常接近的情况下,本文算法成功地把指数级增长的复杂度降低成了线性级的增长。而与其他的算法相比,本文算法也均具有不同程度的优势。
