煤层气藏非对称水力裂缝直井产能评价
2021-06-21李陈
李 陈
(中联煤层气有限责任公司,北京 100015)
0 引 言
目前,主要通过Langmuir方程和Fick扩散定律来描述煤层气吸附、解吸及扩散过程[1-2]。在天然裂缝中的渗流是基于Warren-Root等人提出的双重介质模型[3-4]。李陈[5]等通过定义新的拟时间函数来描述煤层开采过程中的基质收缩效应,使得算法的精度和速度达到商业软件的应用需求。张先敏[6]等建立了低渗透煤层气有限导流裂缝井模型,得出在低渗透情况下直井的压力变化规律。郭涛等分别研究评价了分层合采、压裂水平井等不同开发模式下的产能评价以及影响因素[7-11]。Nie[12]、赵玉龙[13]等人得到了含有人工裂缝的产能评价模型并分析了各流动阶段压力、产量变化情况。
煤层气藏地应力分布复杂,裂缝延伸方向和延伸长度多变,且两翼裂缝长度往往不一致。受煤层较软的影响,裂缝导流因子不会很大,裂缝产能评价需要考虑水力裂缝非对称性带来的影响。该文通过对物质平衡方程的优化,得到非对称裂缝产能评价解析解模型,该研究对煤层气藏产能评价和高效开发具有指导意义。
1 物理模型
气藏中一口压裂直井,压裂裂缝两翼不对称,裂缝为有限导流裂缝,气藏为恒温气藏,垂直方向上不发生流动,裂缝贯穿整个气层,生产条件为定压生产或定产生产。
2 数学模型
2.1 天然裂缝系统渗流数学模型
定义拟压力函数[14]:
(1)
定义新的拟时间函数:
(2)
(3)
天然裂缝物质平衡方程可表示为[5]:
(4)
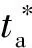
将各变量无因次化:
(5)
(6)
(7)
(8)
(9)
式中:qfD为无因次裂缝流量;xf为裂缝半长,m;qf为裂缝流量,m3/d;qsc为标准状况下流量,m3/d;xD为x方向无因次长度;x为x方向长度,m;yD为y方向无因次长度;y为y方向长度,m;pfD为裂缝无因次压力;pic为标准状况下地层压力,MPa;pf为裂缝压力,MPa;qD为无因次产量;h为地层厚度,m。
通过定义新的拟时间函数及变量无因次化,由边界条件和初始条件,得到式(4)的解:
(10)
(11)
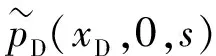
2.2 水力裂缝流动数学模型
定义裂缝偏心因子为:
(12)
式中:θ为裂缝偏心因子;xw为裂缝偏离裂缝中心的距离,m。
无因次化后,裂缝的渗流控制方程为:
(13)
式中:CfD为裂缝无因次导流能力;pD为无因次地层压力;δ(xD-θ)为狄拉克函数。
结合边界条件,式(13)在Laplace空间中的解为:
(14)
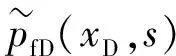
为了得到井底流压解析解,需要耦合水力裂缝流动数学模型和天然裂缝系统数学模型,联立式(10)、(11)、(14)得:
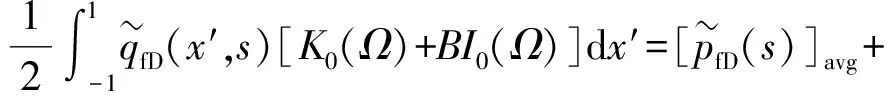
(15)
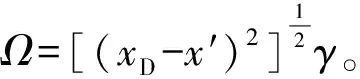
流量归一化方程:
(16)
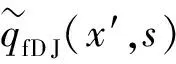
3 历史拟合
在理论解析解求解过程中,需要将生产条件作为方程的定解条件,必须为稳定生产才能够满足方程求解需求。但在实际的生产过程中,井底流压或产量通常是变化的,需利用Duhamel褶积对变化的产量或压力进行叠加,得到变产或变压条件下的理论解析解,进而可以实现理论数据与实际数据的历史拟合,最终在拟合的基础上实现产能评价和产量预测。
变压求产过程与变产求压的区别是变压求产时其产量为未知量,因此,需要先假设一个产量来计算平均压力,在计算过程中不断通过迭代计算来对产量进行修正。
4 结果分析
4.1 准确性验证
为验证文中模型的准确性,选择与煤层气藏解析解经典文献(Anbarci,1990)[2]进行对比,原文献为无限大气藏无限导流裂缝,其裂缝为对称裂缝。文中选取无因次边界xed=10 000,yed=10 000,θ=0.0,CfD=10 000,可近似为Anbarci模型。为了与经典文献进行对比,所有参数量纲与对比文献一致,其中:弛豫时间为13 708 d,黏度为0.010 82 mPa·s,温度为294 K,标准状态下的流量为5 663 m3/d,原始地层压力为3.1 MPa,孔隙度为0.01,井筒半径为0.15 m,综合压缩系数为1.5×10-5MPa-1,朗格缪尔体积为18.6 m3/m3,天然裂隙系统渗透率为26 mD,煤层厚度为1.83 m。图1为文中模型解析解与Anbarci解析解及数值解的对比。
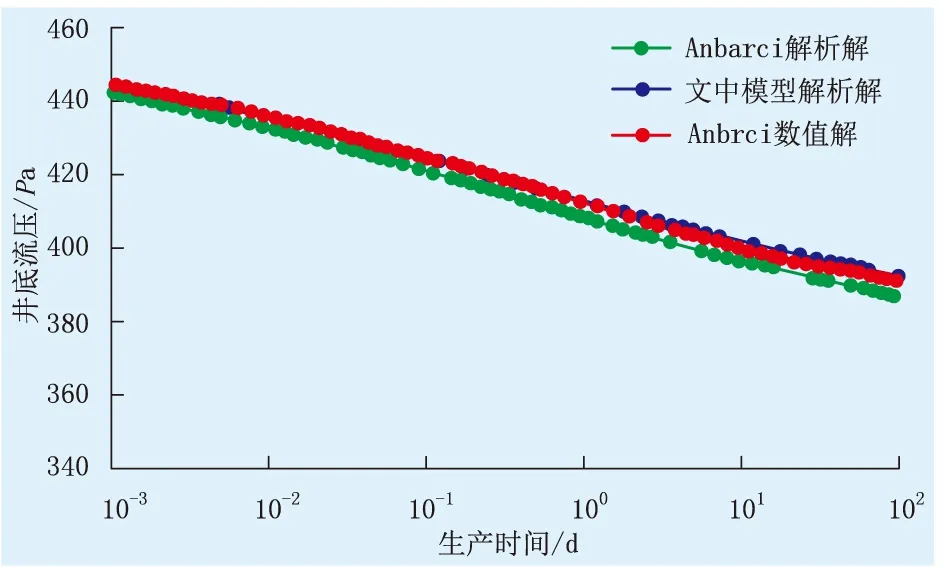
图1 文中模型解析解与Anbarci解析解及数值解的对比Fig.1 The comparison of the analytical solution of the model in thispaper with Anbarci analytical solution and numerical solution
由图1可知,文中模型解析解与数值解的拟合误差要小于Anbarci与数值解的拟合误差,在压力分析中文中模型解析解更加准确,而Anbarci解析解计算结果偏小。
4.2 流动阶段划分
煤层气藏非对称水力裂缝直井渗流状态可以划分为6个流动阶段(图2)。图中σ为速率常数,σ=1 000,ω为裂隙系统存储系数,ω=0.5,λ为裂隙系统窜流系数,λ=100,red为无因次边界长度,red=100,tD为无因次生产时间,CD为无因次井筒存储系数,ΨwD为无因次拟井底流压,ΨwD′为Laplace空间中无因次拟井底流压。
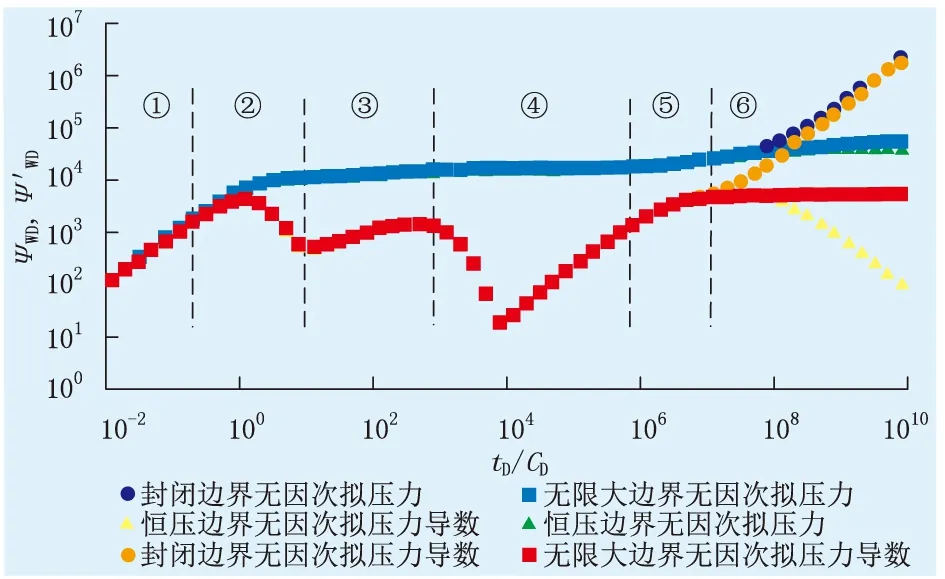
图2 煤层气藏压裂直井不同流动阶段压力响应Fig.2 The pressure response at different flow stages offractured vertical well in coalbed methane reservoir
(1) 井筒储集阶段(图2中①)。该阶段主要反映早期井筒储集效应的影响,无因次拟井底流压和无因次拟井底流压导数均为直线,且2条直线斜率均为1。
(2) 井筒储集过渡阶段(图2中②)。该阶段井筒储集效应逐渐减弱,气藏中的气体逐渐流向井筒,拟压力主要受到气藏和井储效应的影响,无因次拟压力导数曲线逐渐降低。
(3) 天然裂缝到水力裂缝的线性渗流阶段(图2中③)。该阶段可以进一步细分为2个阶段:双线性流阶段和线性流阶段。从双线性流阶段过渡到线性流阶段的过程中,无因次拟压力导数的斜率由1/4过渡到1/2。裂缝的导流能力决定了双线性渗流阶段的长度,一般情况下,裂缝的导流能力越大,双线性流阶段持续的时间越长。由于无因次拟压力在该阶段只有轻微的降低,因此,基质的解吸现象不明显。
(4) 基质解吸、气体扩散作用阶段(图2中④)。随着拟压力的进一步降低,解吸现象变得越来越明显。该阶段吸附气逐渐通过解吸附从基质中解吸出来变为自由气,使基质周围的气体浓度增加,气体通过扩散作用进入天然裂缝系统。无因次拟压力导数呈现“V”字型。“V”字型的深度和持续时间由井筒存储系数、储容系数、解吸系数以及窜流系数决定。该阶段也是煤层气、页岩气等具有吸附解吸现象气藏的特征阶段。
(5) 拟径向流动阶段(图2中⑤)。该阶段气体从基质中解吸出来扩散到天然裂缝系统,这一过程与气体从天然裂缝流入人工裂缝系统的过程达到动态平衡,拟压力的下降速率变小。
(6) 边界控制流阶段(图2中⑥)。在有边界的气藏模型中,压力波到达边界后,对于恒压边界气藏而言,由于边界能量供应充足,压力较快达到稳定状态;对于封闭边界系统,压力系统达到拟稳定状态。
4.3 裂缝非对称程度影响分析
裂缝两翼非对称程度不同,井底流压反应不同。图3为非对称裂缝的无因次压力变化情况。
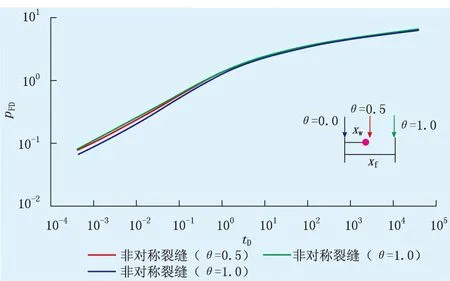
图3 裂缝两翼非对称程度不同压力曲线Fig.3 The pressure curves at different asymmetricdegree on two wings of fracture
由图3可知,当θ=1.0时,表示裂缝完全在井的一边,为单翼裂缝;当θ=0.5时,表示井在裂缝的3/4处;当θ=0.0时,表示井在裂缝中心处,为对称裂缝。
由图3可知:在相同产量的情况下,对称裂缝的压降要小于非对称裂缝,因为在气体生产过程中,气体在非对称裂缝中的渗流阻力较大,消耗能量较多,地层能量利用率较低,自然产收率较低,因此,最佳的裂缝形态为中心对称裂缝。
图4为不同导流能力下井底流压变化情况。由图4可知,当裂缝导流能力越大时,裂缝非对称性对井底流压影响越小。一方面,水力裂缝的导流能力远大于天然裂缝,气体在裂缝中渗流所消耗的能量比在天然裂缝中小得多,天然裂缝系统是决定能量消耗的主体;另一方面,水力裂缝容易提供一个通畅的流通路径,以满足天然裂缝中渗流出来的气体在其中渗流。裂缝的导流能力越小,裂缝非对称性所带来的差异越大。对于煤层气藏,由于煤储层较软,其水力裂缝导流能力通常较差,非对称性裂缝对井底流压影响较大。因此,对称裂缝为地层能量利用率最高的裂缝,在煤层气藏储层改造过程中,应尽可能压裂形成对称裂缝以降低气体渗流的能量消耗。生产后期,对称性不同、导流能力相同的裂缝无因次井底流压逐渐重合,表明非对称性对产能评价的影响主要发生在生产前期。
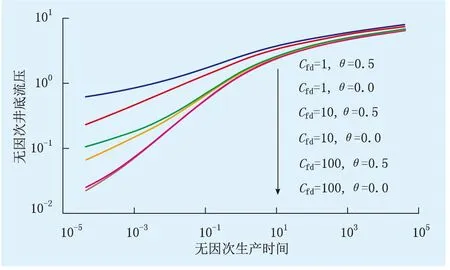
图4 不同导流能力下井底流压变化情况Fig.4 The variations of downhole flow pressure at different conductivity
5 现场实例
沁水盆地A区块Well1—Well4井位于西山煤田中北部古交矿区,属于晋中断陷,区块构造相对简单,断层发育较少,地层稳定,但受后期构造运动影响,该区域一个向斜构造核部挤压形成一个“鼻状”构造,导致附近地层应力分布不规则,微地震监测显示水力裂缝两翼的长度不一致。通过压裂模拟及试井分析研究发现,裂缝导流能力较差,改造措施效果不理想,常规模型产能评价时历史拟合效果较差。根据裂缝延伸效果,需要采用非对称裂缝模型进行产能评价。以Well1井为例,考虑裂缝非对称性对其井底流压和产气量进行历史拟合(图5),拟合误差明显降低,尤其是当裂缝导流因子较小时,裂缝偏心因子的引入可以更好地改善拟合效果。表1为Well1—Well 4井压力、产量历史拟合误差情况。由表1可知,该区块4口井压力拟合误差由31.0%降至7.0%,日产气量拟合误差由20.0%降至6.5%,4口井平均偏心因子为0.225,在水力压裂实施的过程中,裂缝非对称性较为严重,平均裂缝导流因子为65,相比于常规气藏及其他页岩气藏,裂缝导流能力较弱。
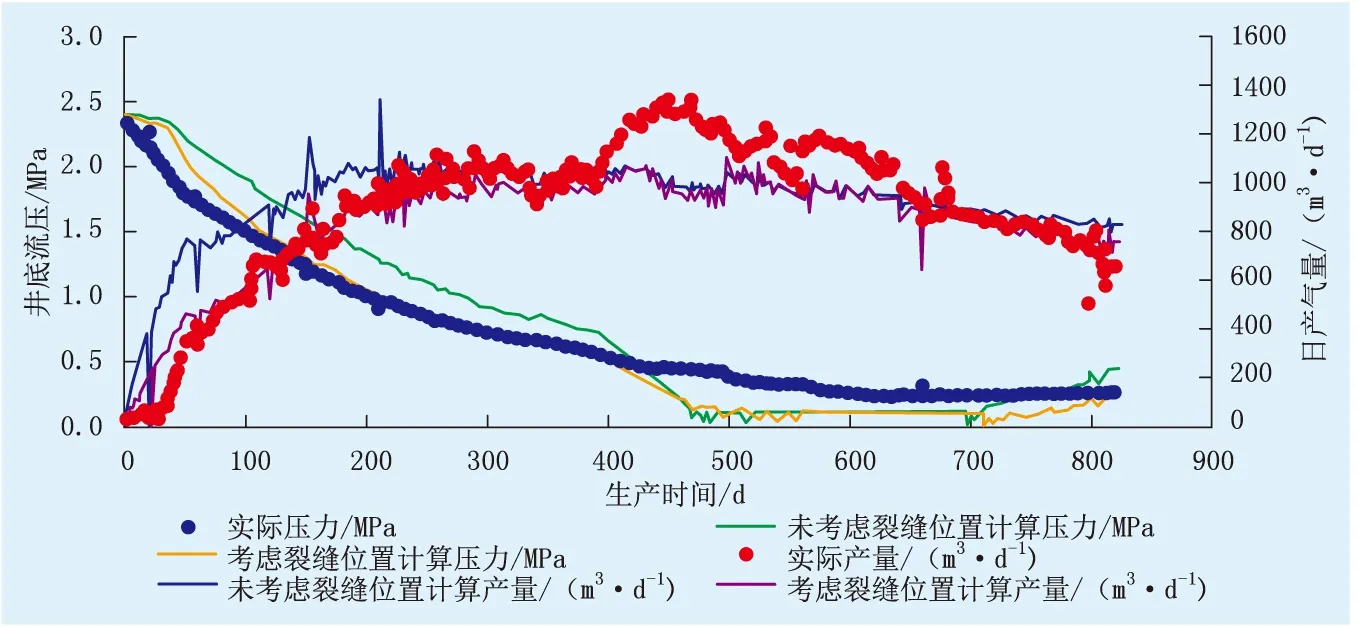
图5 Well1井底流压、产气量历史拟合Fig.5 The history fitting of downhole pressure and gas production of Well 1
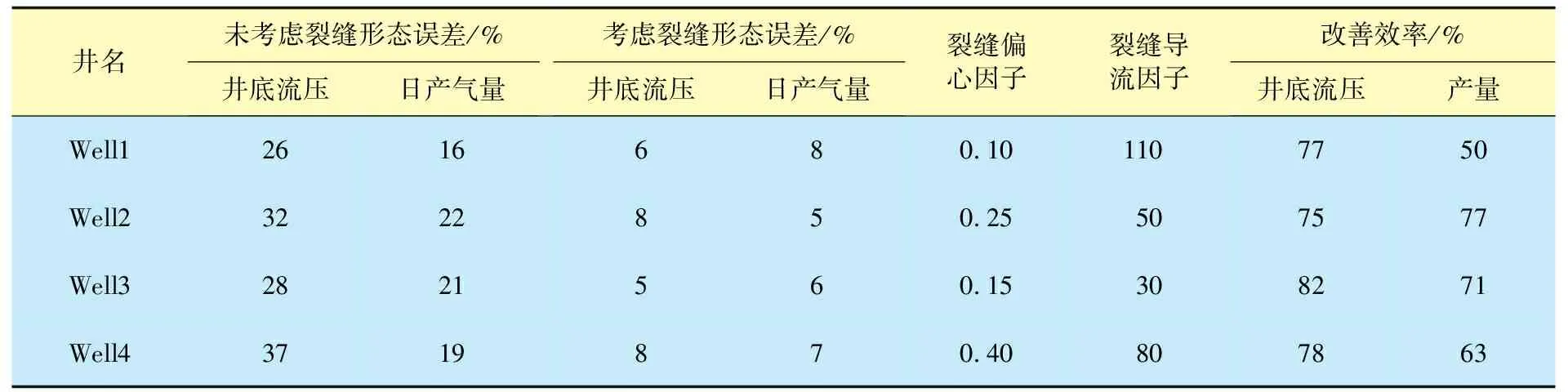
表1 井底流压、产量历史拟合误差Table 1 The error of history fitting of downhole pressure and gas production
6 结 论
(1) 建立了考虑裂缝非对称性的产能评价模型,通过Duhamel褶积,解决了变流压生产或者变产量生产问题,达到了解析解模型与历史生产数据拟合的目的。
(2) 对称裂缝为地层能量利用率最高的裂缝,裂缝的非对称性对单井产能的影响程度会随着裂缝导流能力的降低而增加,影响主要发生在生产前期。
(3) 沁水盆地A区Well1—Well4井水力裂缝非对称性较强(裂缝平均偏心因子达到0.225)、导流能力较弱(平均裂缝导流因子为65),考虑裂缝非对称性能够明显改善拟合效果,压力拟合误差由31.0%降至7.0%,日产气量拟合误差由20.0%降至6.5%,有效提高了预测精度。
