基于改进头脑风暴算法的无线充电路径规划

边锐锋

（武汉理工大学自动化学院，湖北 武汉430070）

1 引言

在具有充电结构的无线可充电传感器网络[1]（WRSN）中，节点主动监视其自身的剩余能量，当其能量水平低于某个阈值时，向数据中心（DC）发送充电请求。DC对请求节点建立充电调度队列，并将调度发送给移动充电器（MC）从而进行充电服务。为了减少移动充电器在路上的能量消耗，需要合理规划移动充电器的充电路线。路径规划问题属于传统的TSP问题。但是传统TSP算法并不适用于非接触式无线充电的路径规划，未考虑到充电有效圆域的影响。针对上述算法存在的问题，本文通过引入可行充电圆域的概念对传统的TSP算法进行相对应的改进。

2 有线充电设备路径模型

假设在一个WRSN系统中存在N个无线传感器，一个数据中心，一个移动充电器。定义传感器的坐标为：

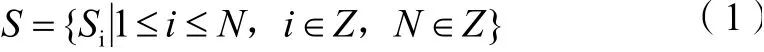
式（1）中：Si为第i号传感器对应的坐标位置。

当不考虑充电半径R存在的情况下（即为有线充电设备），此问题则变化为传统的TSP问题，则MC的充电路线可表示为二维有限序列：

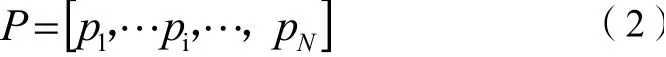
将MC行驶路程作为优化目标可以得到目标函数如下：

式（3）中：L（Pn）为充电路线Pn对应的总路程；为充电路线中DS对应的二维坐标。

即可得整体优化模型为：

3 无线充电设备的模型建立

3.1 充电半径不重叠

当MC为无线充电设备时，将其无线充电的有效圆域半径标记为R，且假设在此有效距离内充电场的能级不随距离而发生变化，即只要MC位置坐标pm（xm，ym）与传感器i的位置坐标si（xsi，ysi）满足d（pm，si）≤R时，其对传感器i的充电效率就将等于R（ma/s）。在此情况下，若充电有效距离R满足：

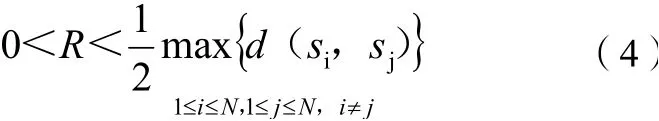
图1 充电线路大致图

显然在该情况下充电半径之间互不重叠，该情况下的最短路径仍然为首尾相连的折线段，且听蹲点数量仍然等于传感器的数量，即MC的充电路线仍可表示为二维有限序列：

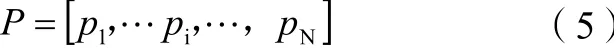
式（5）中：pi（xi，yi）为MC进行充电操作时的停留点位置坐标，其必须满足充电距离约束，且每个传感器的可充电范围内至少停留了一个MC，表示为：

MC在各个停留点最多对同一传感器充电，且不会在多个停留点对同一个传感器充电，表示为：

长 短 时 记 忆（Long short term memory，LSTM）型RNN模型是传统RNN的改进。它主要解决了RNN模型的梯度爆炸和梯度弥散的问题。如图2所示。LSTM接受上一时刻输出，当前时刻系统状态以及当前系统输入，通过输入门，遗忘门和输出门更新系统状态并输出最终结果。

即表示任意两个停留点的冲带你目标互不相同，且所有传感器都需要被充电，即：

式（7）中：S为全部传感器坐标的集合，即表示所有停留点的充电目标的集合包含了所有的传感器。

目标函数仍为MC的充电总路程，即：

整体模型可以表示为：

3.2 充电半径相互重叠

当充电有效距离R较大，多个传感器的可充电范围发生重叠时，即R满足此时的充电路线如图2所示。

从图2中可以看出，当可充电区域相互重叠时，让停留点落在重叠区域内。

即使得MC可同时对多个目标传感器进行充电。显然在此规则之下，若有k个传感器的可充电区域发生重叠，则对应的停留点数量将会变成30-k个，即充电路线可表示为

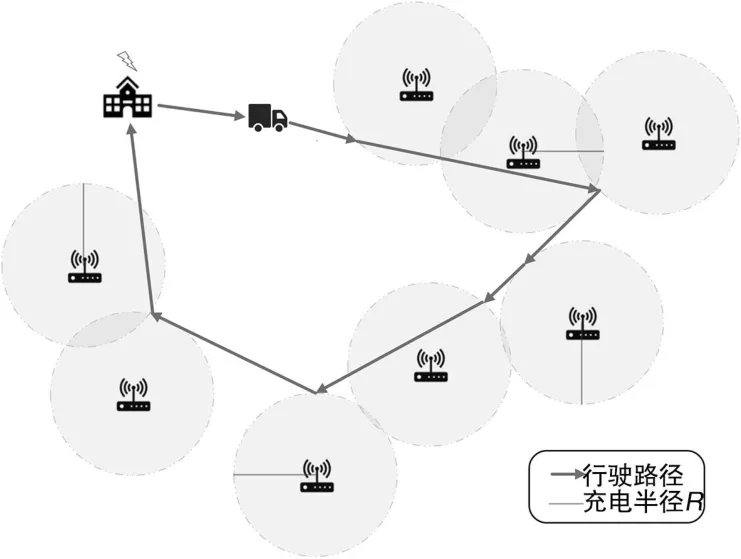
图2 充电路线示意图

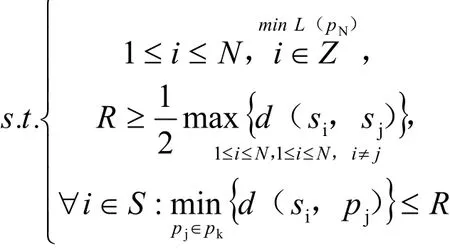
4 嵌入随机梯度下降算法的头脑风暴算法

4.1 头脑风暴算法（BSO）

本文使用头脑风暴算法求解的步骤如下：①初始化。根据题目，在接的可行域中随机选择n个个体xi，作为优化问题的初始解，其中n=1，2，…，N，确定最大迭代次数Lmax，设定算法终止条件。②聚类。用dck-means聚类算法将n个个体分成m个类，计算每个个体的适应度函数值，适应度最好的个体记为该类的中心个体。③编译。随机产生一个[0，1]之间的随机数Po1，若大于预先设定的概率参数Po，随机选中一个类的中心个体，替换为随机产生的新个体。④生成新个体。首先产生[0，1]之间的随机数pa1，与预先设定的概念参数p1进行比较，跟会员结果选择一下方式产生候选个体xs。⑤改进。在头脑风暴的算法中，在传感器中所处位置建立可行圆域，当停留点位于可行充电圆域内部的时候，将其所对应的传感器列入到禁忌传感器范围中。

4.2 随机梯度下降算法

在无线充电半径R＞0时，采用随机梯度下降（SGD）对BSO的目标函数L（Pk）进行寻优，采用单个训练样本的损失来近似平均损失，即：

式（8）中：P为中心位置；θ为参数方程圆周上的角度；为pi到pi+1点的直线距离。

模型参数θ的更新公式为：

式（9）中：η为学习率。

将求得的θ代入到目标函数中求得最短路径后，作为适应度带入到基因中并执行头脑风暴算法。

5 实验结果

为了验证算法的可行性，选取1个数据中心、29个传感器以及1个MC作为前提条件。对于有线充电设备，当R=0时，采用头脑风暴算法解决传统TSP问题，其结果如图3所示。总距离为11 482.802 89 m。

其充电设备规划路线为：

传统的TSP算法并不能解决带有充电半径存在的TSP问题，使用改进的头脑风暴算法进行求解可得。

当0＜R＜88.53 m每个MC在任意位置最多同事给一个传感器充电，假设充电半径为50 m，通过本文的算法可以解得总距离为11 051.789 2 m。改进头脑风暴解决非接触式TSP结果如图4所示。

当R≥88.53 m时可同时对多个传感器充电。总距离为9 251.937 8 m，移动路径如图5所示。

可以发现相较与传统的TSP算法，本文中的算法可以充分考虑到充电半径的影响，减少了MC在线路上的能耗。最后对算法的迭代次数进行分析，如图6所示。对算法进行灵敏度分析，如图7所示。从图6中可以看到，在趋近于300次迭代次数的时候，寻得最优解。从图7中可以看到，在充电半径不断增大的情况下，最短路径的下降曲线较为平滑，灵敏度处于比较好的状态。

6 结语

本文中提出的算法可以有效解决非接触式的路径规划，算法普适性，在实际应用中可有效降低充电周期，减少线路能耗。本算法在充电半径过大的时候会引起最优解局部震荡，使得收敛速度在半径过大时较慢，但是仍能得出最优解。

图3 头脑风暴算法解决传统TSP结果图

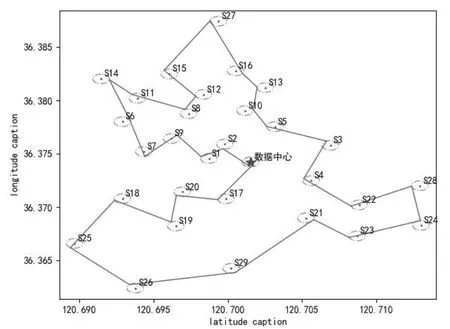
图4 改进头脑风暴解决非接触式TSP结果图

图5 移动路径示意图

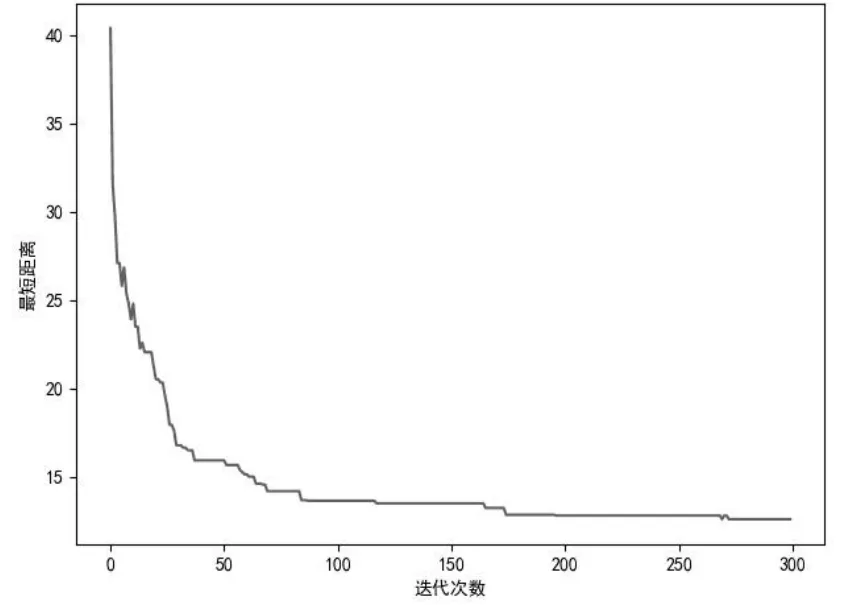
图6 对算法的迭代次数进行分析

图7 对算法进行灵敏度分析