卫星地影模型及计算方法研究综述

李 畅，贺景瑞，李 懋，赖 鹏

（中国人民解放军63795部队，北京100089）

1 引言

太阳、地球和卫星，三者在太空中依据其轨道运行规律不停变换相对位置关系。在某些特殊时间和条件下，卫星处于地球相对太阳背面，从而受地球遮挡无法接收太阳光，此类现象叫做“地影”[1-2]，如图1所示。

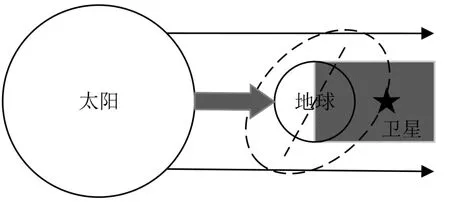
图1 地影示意图

作为天体运动不可避免的现象，“地影”的覆盖范围相当广泛，包括地球同步静止轨道卫星、太阳同步轨道卫星等各类型卫星基本上都会面临地影约束。例如GEO卫星地影期出现在星下点当地春分、秋分前后，每期延续天数约46 d，单次最长地影时长约72 min[3]。由于“地影”期间太阳光被地球遮挡，在缺失阳光这一太空中最重要的自然能量来源后，航天器在轨健康运行管理将面临严峻考验[4]。

首先，地影期间航天器无法接收太阳光，部分赖以依靠阳光工作的部件将失去效能。如太阳帆板无法采集能量进行光电转换，卫星系统只能通过星载蓄电池进行放电供电。同时，太阳敏感器也将无法正常开展工作[5]。其次，在无光照条件下，航天器表面温度将会出现骤降，这对卫星热控防护提出了较高要求。此外，缺乏太阳光直射意味着卫星受到太阳光压摄动影响消失，将会引起航天器不同程度姿态和轨道变化[6-7]。因此卫星地影精确预报对在轨航天器长期安全运行和工作效能充分发挥具有重要意义，同时其特征规律也可对卫星总体设计提供参考和建议，加快新技术、新方法研究应用[8]，如智能充放电管理、零部件温度余量设计等。

综上所述，本文将从模型分类、判定标准、计算方法、总结与展望等方面对“地影”问题进行分析，行文思路如图2所示。

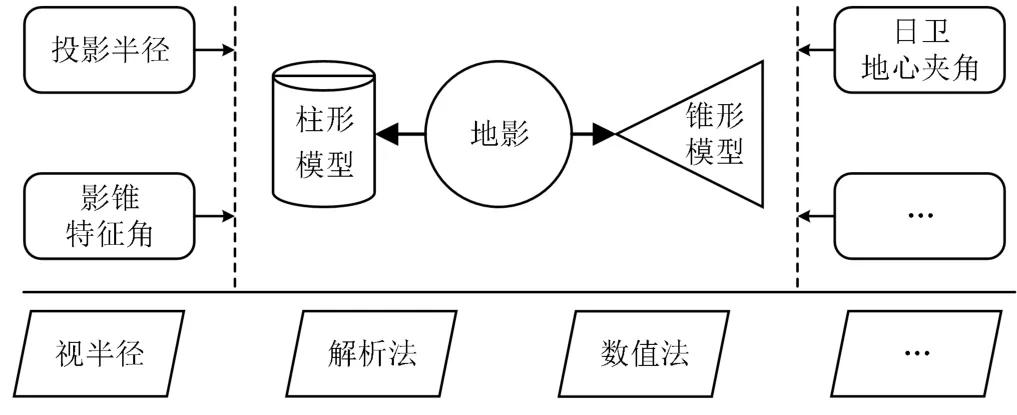
图2 文章结构图

2 地影模型

1957-10-04，世界第一颗人造卫星——人造地球卫星1号发射升空。紧随其后，1958年太阳能电池阵开始应用于卫星供电[9]，对其有重要影响的地影问题研究迅速展开。目前，较为通用的地影模型有两种，分别是柱形地影模型和锥形地影模型，二者关键区别在于是否将太阳视为点光源[10]。下面对这两种模型进行详细阐述。

2.1 柱形地影模型

在柱形地影模型中，太阳作为非点光源存在，即将太阳光视作平行光束。受地球阻挡，在其后方形成“圆柱形”的阴影区域，因此称为柱形地影模型，当卫星飞行至该区域时即进入地影期。在此模型中，卫星状态分为有光照和无光照两种，如图3所示。

柱形模型认为太阳、地球间距离足够远、太阳半径足够大，可抵消太阳光在传播过程中产生的方向畸变。从数值来看，相对于太阳半径（6.963×105km）和地球半径（6.371×104km），日地距离（1.5×108km）已超出二者三四个数量级。基于此，部分学者认为即便是高轨卫星在定轨弧段不太长时，采用圆柱形地影模型仍可以将精度保持在米级范围[11]。

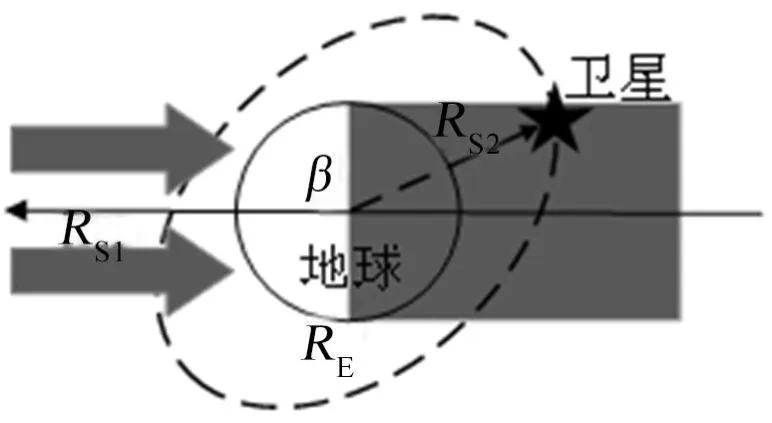
图3 柱形地影模型

2.2 锥形地影模型

然而，随着各类工程应用对卫星姿态确定精度的要求越来越高，柱形地影模型中太阳光为平行光束前提已无法被轻易忽视。研究指出柱形模型仅适用于低轨卫星阴影计算，对于高轨卫星计算误差将越来越大[12]，时间相差甚至达1 min以上[13]。因此，需精确考虑太阳光传播实际情况、太阳和地球半径及日地距离，锥形地影模型应运而生，如图4所示。太阳光与地球形成的阴影区如同圆锥形状，故称为锥形地影模型。该模型将卫星所处区域分为四类，分别是全影区（完全无光照）、半影区（部分光照）、光照区（完全无遮挡）和伪影区。其中，伪影区因距地球过远，通常不作考虑。

2.3 常见判定条件

在两种模型描述地影问题的几何关系基础上，众多研究学者利用不同的阴影区物理量标准得到了不同的判定条件和约束方程，这些物理量标准主要有日卫地心夹角、影锥投影半径和影锥特征角等[14-15]。下面对这些判定方法进行阐述。

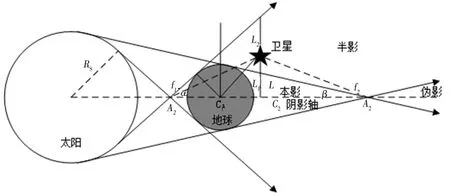
图4 锥形地影模型

2.3.1 日卫地心夹角

日卫地心夹角判定标准通常用于相对简单的柱形地影模型。在图3中，RS1表示太阳地心矢量，RS2表示卫星地心矢量，RE表示地球半径。根据相对位置关系可得卫星处于阴影期的限制条件[16]：卫星和太阳地心矢量夹角β大于90°，且卫星处于地影阴影柱范围之内。公式如下：

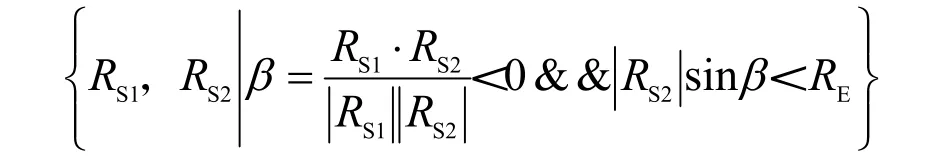
2.3.2 影锥投影半径

如图4所示，设定L为卫星在阴影轴（即日地连线）上的垂直高度，L1为本影边界在阴影轴上的垂直高度，L2为半影边界在阴影轴上的垂直高度。C1和C2分别为卫星至前照点A1、后照点A2在阴影轴上的距离。通过计算各参数值并比较各参数之间的大小（如表1所示），可确定卫星所处区域的光照条件。

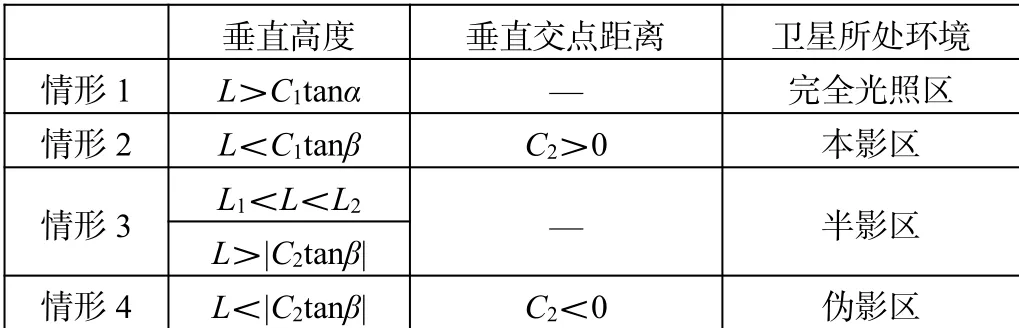
表1 卫星光照条件判定

2.3.3 影锥特征角

影锥特征角的定义为，以A1为顶点的半影圆锥和以A2为顶点的本影圆锥的半锥角，分别用α和β表示，易知本影圆锥嵌套于半影圆锥中。在地球周年绕日运动中，日地距离变化范围为1.47×108～1.52×108km，β变化范围分别为0.264 8°～0.273 8°和0.260 0°～0.268 8°，变化率分别为5.707 8×10-10°/s和5.580 9×10-10°/s，可知二者变化均极小，可视为常数[17]。

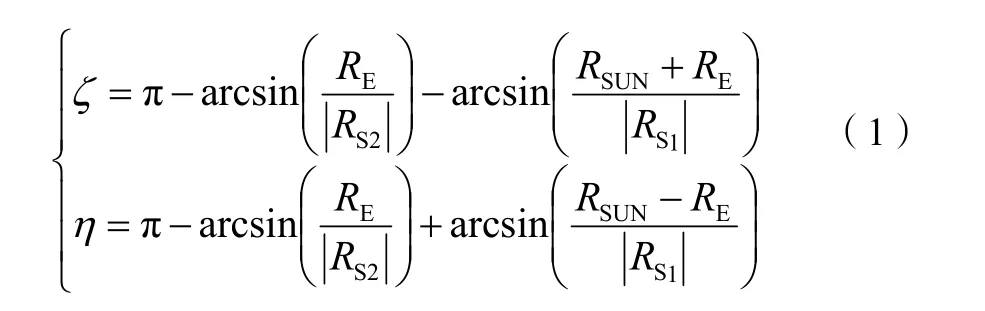
此方法判定思路为，首先计算出卫星至A1、A2点与阴影轴的夹角，分别用ζ和η表示[18]，计算方法见公式（1）。卫星若处于阴影中，则满足ζ＜α、η＜β，同时满足卫星在地表之上的距离限定条件。

不难看出，本判定标准与影锥投影半径判定标准本质相同，都是出于本影、半影锥形角来限定地影边界，不同的是后者应用长度来代替角度进行判定。对于上述两种判定条件，谢文杰等进行了仿真和验证，结果证明相较于影锥投影半径判定法，影锥特征角的计算精度和计算效率明显提升[17]。影锥角条件判定如图2所示。

表2 影锥角条件判定

3 计算方法

在根据地影模型得到不同判定标准和约束方程后，如何精确求解方程的同时又保证计算效率，成为了诸多学者研究的重点。在计算方法方面，主要分为天体视半径计算法和轨道根数计算法两种。

3.1 天体视半径法

太阳遮挡示意图（卫星视角）如图5所示。此方法基于卫星视角，计算此视角下未受遮挡的太阳视面积，通过与标准太阳视面积比较判断卫星是否处于地影期。具体计算方法为，设计算地球视半径为a，太阳视半径为b，两天体中心点视距离为c。则太阳视面积（未受遮挡区域）计算公式为：

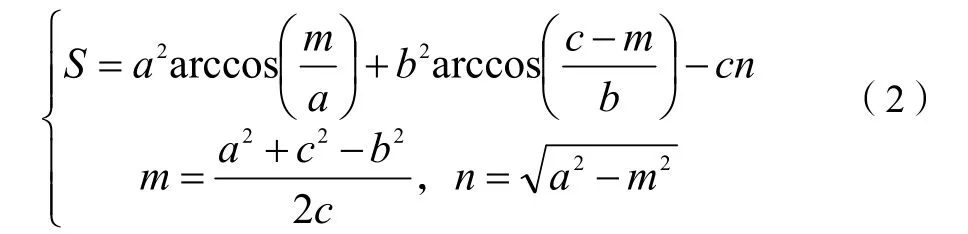
由公式（2）易知当S=πb2时，卫星处于完全光照时期；当0＜S＜πb2时，卫星被部分遮挡；当S=0时，卫星则处于阴影区[19]。然而此种方法存在精度较低问题，原因为太阳距离地球、卫星较远，导致卫星视角下太阳角半径很小，经计算视半径约为相对的计算误差较大，因此不适用于高精度计算[13]。

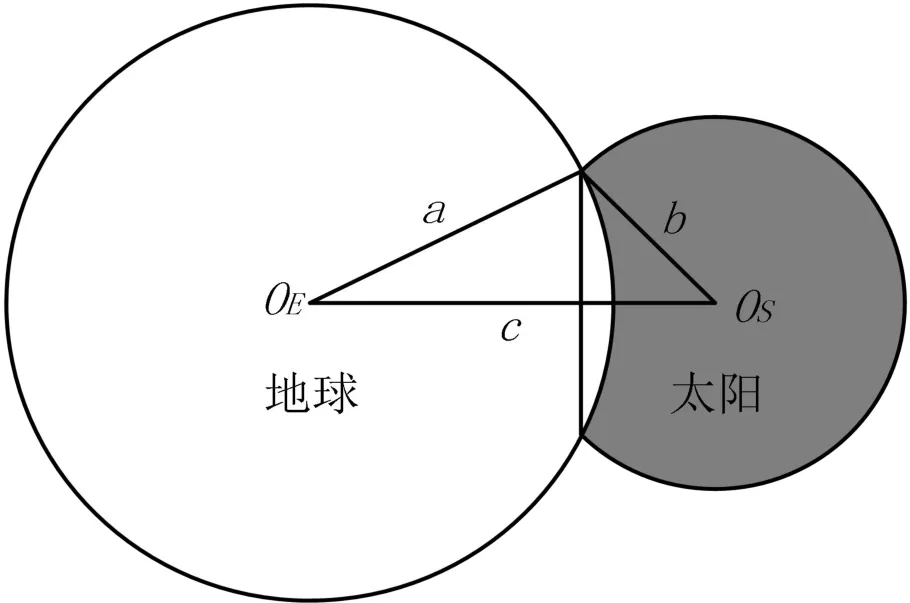
图5 太阳遮挡示意图（卫星视角）

3.2 轨道根数法

顾名思义，轨道根数法利用卫星轨道六根数、卫星运动方程以及地影判定条件进行求解，主要分为解析法和数值法。

3.2.1 解析法

求解地影进/出时间本质上是解方程问题，联立卫星运动方程和阴影约束方程（公式3），可得到一个一元四次方程，如公式（4）所示：

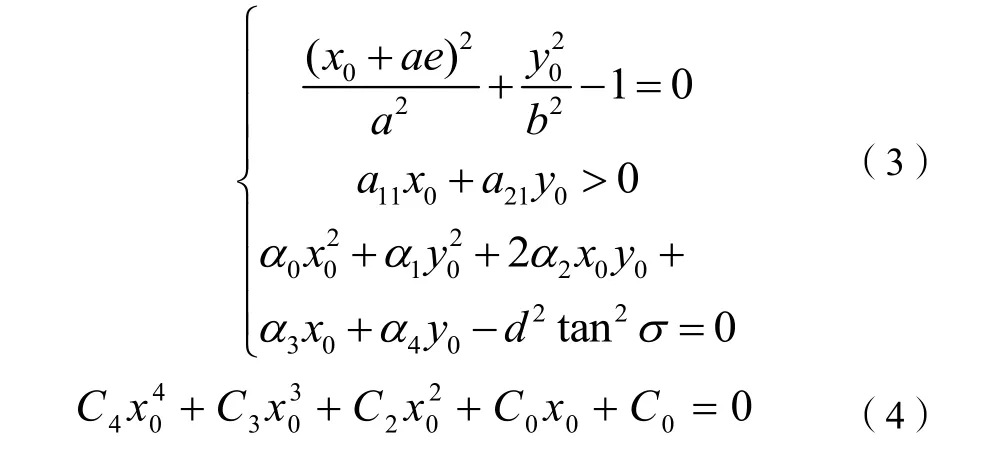
式中Ci包含三角函数和实时变化的日地距离、地心至A1和A2距离等复杂项，因此得到精确的方程解析解几乎不可能。张世杰等通过简化上述方程中的变化小量，得到实系数四元方程及近似解，然而却导致精度下降[20]。这也是解析法面临的主要困难。

3.2.2 数值法

部分学者研究表明，对于受摄轨道的动力学方程，数值方法求解是唯一途径[21]。相比于解析法，数值法可以解决四次方程精确求解问题，能够充分利用卫星高精度定轨参数，将地影计算精度保持在同等水平。然而数值法也存在一些缺陷：因涉及到大量数值积分运算导致计算量较大，不适合长时间大跨度地影规律统计和计算[22]，需要适当增加积分步长，而积分步长增加后往往导致精度下降；由于光压摄动在边界突然消失或出现，导致数值法在地影边界计算时存在“间断”问题[23]。

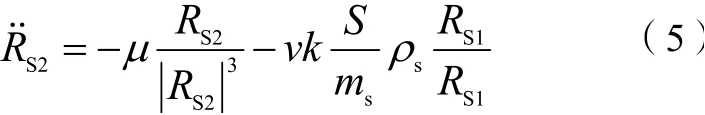
公式（5）为卫星运动基本方程，其中v为蚀因子，ρs为光压强度。卫星处于地影中时取0、地影外取1。由于v的非连续性，在进出地影时公式（5）的右函数会出现间断，导致误差增大，从而影响计算精度。

针对数值法存在问题，王歆和刘林展开计算并验证了间断对计算的影响程度，并对单步法和多步法进行算法改进和验证；贾向华等提出了一种变步长的积分数值方法，在阴影预报时逐步减小计算步长，同时保证了计算精度和计算效率[10]。陈刘成通过应用改进Encke积分方法，调整积分步长和节点，实现单步法误差在厘米级下；通过选择合适的积分步长，可将多步法对柱形地影模型和锥形地影模型跨边界带来的积分误差双双控制在厘米级下[23]。

4 总结与展望

通过对比两种地影模型可知，柱形地影模型代表着一种简化、近似的方法，判定条件和计算方法简单，适用于中低轨卫星地影的快速计算；而锥形地影模型能够更加真实地反映太阳、地球、卫星三者实际情况，完善了限制条件导致计算量加大，能够覆盖各轨道卫星计算需求，已成为高精度阴影预报的不二选择。模型对比如表3所示。

基于上述研究进展，如今卫星地影预报已达到了相当精确的程度，可满足地影期间卫星电源系统、姿轨控系统、热控系统及重要器件防护对时间精确度的要求，相关应对措施及设计研究进展已颇具成效。崔波等针对高轨卫星的锂离子蓄电池组自主管理系统，充分考虑地影期影响，设计了分模式管理方法并进行了实际验证[24]；吴文瑞等结合地影模型，对太阳同步轨道热控分系统进行了分析与优化[25]；严灵杰通过分析地影等干扰因素，完善了光电跟踪系统的位置预测算法[26]。未来将以星上自主解算、自主判断、自我管理等方向为目标，提高星上运算能力，增强卫星抗地影能力和智能化运行管理发展。

表3 模型对比