考虑量化输入和输出约束的互联系统自适应分散跟踪控制

秦贞华 何熊熊 李刚 伍益明

在过去的几十年中,不确定互联系统的分散自适应控制一直是控制领域的研究热点问题之一.所谓分散控制策略是指对每一个子系统利用局部信息而非全局信息来设计控制器.相比单个系统,子系统之间的互联关系使得分散控制设计成为挑战.基于子系统输出的不确定多项式组成互联项这一假设,文献[1] 讨论了大型互联系统的分散自适应控制设计.由于具备能够改善系统瞬态性能的优点,反推(Basckstepping)法成为处理不确定性线性或非线性控制系统的有效方法之一.文献[2] 首次提出基于反推法的分散自适应控制策略.针对含有未知不确定项的非线性互联系统,文献[3-6] 通过融合反推设计法和神经网络或模糊系统,设计分散控制律.但是,文献[1-6] 的控制方法仅适用于输出调节控制问题,即所有子系统的输出最终趋于零.当考虑输出跟踪问题时,控制任务变得更复杂,原因在于被跟踪的非零期望轨迹将通过子系统之间的交互,影响其他子系统的动态.文献[7-9] 讨论了互联系统的输出跟踪问题.其中,文献[9] 讨论完全分散输出跟踪控制问题,通过引入光滑非线性函数项消除来自其他子系统互联项的影响.文献[10] 放宽了[9] 的条件,假设子系统包含未知非线性项且互联函数上界为未知常数,然后基于反推法设计了自适应跟踪控制器.总结已有研究成果,通常对互联项的假设条件是,互联项的平方上界为每个子系统输出项的光滑函数与表示子系统间互联强度的已知常系数的乘积的和[11],或者互联项绝对值的上界为每个子系统的输出项绝对值与输出项的光滑函数以及表示子系统间互联强度的未知常系数的乘积的和[12].但文献[12] 的假设条件只能应用于解决互联系统输出稳定问题,对于互联项互联强度常数项未知的输出跟踪问题,如何进行控制设计,目前鲜有相关研究成果.

量化控制系统设计对于研究数字控制和网络控制系统有十分重要的理论和实际价值,因此近年来也是控制领域研究热点问题之一.量化控制的关键问题是如何平衡低通信率和控制精度之间的关系.目前,关于输入量化的研究成果已有很多[13－15].然而,这些成果都是基于量化参数已知的情形设计的鲁棒或自适应量化控制方法.文献[16] 针对量化参数未知的情况讨论不确定系统的自适应量化控制问题,作者设计自适应律来估计未知量化参数组合的向量而不是未知参数本身,而且其所考虑系统模型的不确定项是参数化表达而非完全未知项.文献[11]引入双曲正切函数设计自适应量化跟踪控制器,并将这个方法扩展到含有未知项的互联系统.

为了避免控制系统在运行过程中出现故障或维持期望的性能指标,要求我们对实际被控系统的状态或输出加以约束限制.在实际操作过程中,一旦违反约束会导致系统性能下降,甚至损坏设备或出现不可逆情况.因此,考虑具有输出约束的非线性系统控制设计一度受到控制界学者广泛关注,并取得了许多重要研究成果.为满足输出受限要求,文献[17]针对非线性单输入单输出系统引入障碍李雅普诺夫函数,并基于此设计控制器.基于此,Han 等在文献[18] 中利用动态面控制技术解决了“计算膨胀问题”.进一步,He 等将此方法扩展应用到柔性起重机系统的输出受限控制[19].文献[20] 针对非严格反馈形式的大型互联系统,设计自适应模糊分散控制律,保证系统在有限时间内达到输出跟踪目的,同时,基于障碍李雅普诺夫函数的设计方法,保证了系统输出不违反约束条件.

基于以上分析,本文针对一类非线性互联系统,在系统存在未知非线性的情况下,考虑输入量化和输出约束,设计自适应分散跟踪控制协议.不同于文献[11],本文假设互联强度为未知常数,并分别针对量化参数已知和未知两种情况,基于自适应反推法和神经网络任意逼近特性设计控制策略.此外,障碍李雅普诺夫函数的引入,确保了系统的输出不违反约束条件.数值仿真验证了所提方法的有效性.

本文主要内容组织如下:第1 节介绍系统模型,给出设计过程需要用到的假设和引理以及神经网络相关预备知识,并提出要解决的控制问题.第2 节分别针对量化参数已知和未知两种情形,基于自适应反推技术给出互联系统控制器的设计过程以及稳定性分析.第3 节给出数值仿真以验证所提方法的有效性.第4 节总结本文主要工作.

1 问题描述及预备知识

1.1 问题描述及基本假设

考虑如下具有量化输入的N 个关联子系统复合组成的非线性不确定互联系统,其中子系统j 的动力学方程为

其中,xj=[xj,1,xj,2,···,xj,n]T∈Rn是子系统的状态向量,[y1,y2,···,yN]T∈RN是子系统的输出向量且满足约束|yj|≤kc1,∀t ＞0,kc1＞0,fj,i(·)为未知光滑函数,表示子系统的非线性项,Δj,i(·)为未知光滑函数,表示子系统之间的互联项,qj(uj)∈R和yj∈R分别是子系统的实际输入和输出,qj(uj)取uj的量化值.量化函数选取如下[11]

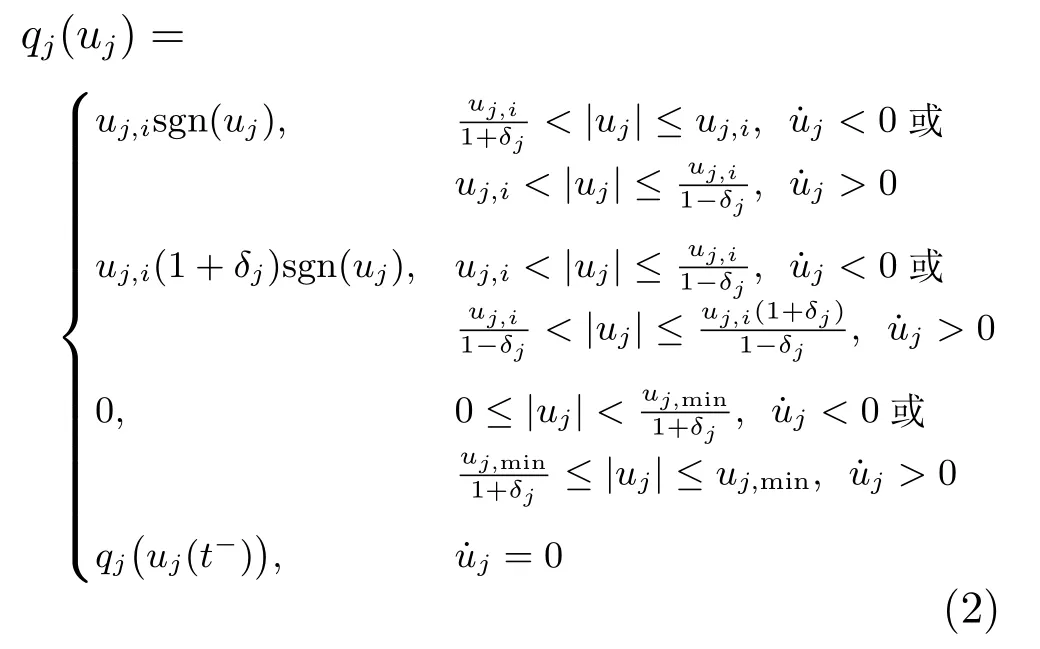
假设1.非线性互联项满足

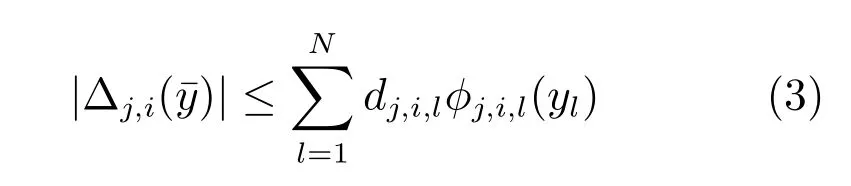
其中,φj,i,l(·)为已知光滑函数,dj,i,l＞0 表示不确定子系统之间相互作用的强度,即互联强度.

注1.量化器分为两类:均匀量化和非均匀量化.对数(Logarithmic)量化和滞后(Hysteresis)量化属于非均匀量化,即信号的量化间隔不相同.如文献[11] 所述,相比较对数量化器,滞后量化能够自动调节量化强度,从而避免抖振现象.因此,本文选择后者用于量化器设计.

注 2.∑文献[11] 假设条件为即互联项的平方上界为所有子系统互联强度与已知光滑函数乘积的和,并且互联强度为已知常数.文献[12] 的假设条件为其中互联强度ρi,j,k为未知正常数,但此假设条件仅适用于解决输出稳定问题,对于输出跟踪问题却不适用.本文所提假设条件不仅满足互联强度为未知常数,而且适用于输出跟踪问题,因此放宽了文献[11]和文献[12] 的假设条件.

假设2.存在正常数Y0,Yn且有使得参考跟踪信号yj,r和i 阶导数满足|yj,r|≤Y0,

引理1[14].存在函数gj(uj)和dj(t),使得量化器函数被分解为

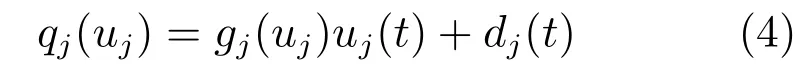
其中,函数gj(uj)和dj(t)分别满足1-δj≤gj(uj)≤1+δj和|dj(t)|≤uj,min.

引理2[17].对任意正常数kj,d1,定义开集Z1={zj,1⊂R:|zj,1|＜kj,d1}⊂R,N=Rl×Z1⊂Rl+1.考虑系统

其中,η=[w,zj,1]T∈N 是状态变量,函数h :R+× N →Rl+1是分段连续函数,且满足局部李普希兹条件.假设存在连续可导正定函数U :Rl→R+和V1:Z1→R+,i=1,2,···,n 使得

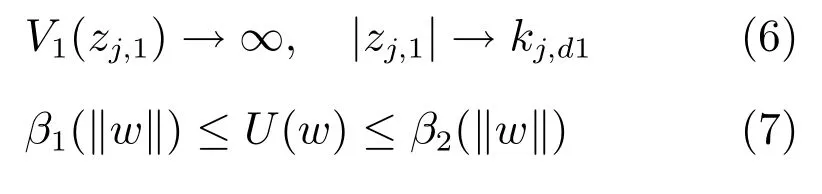
并且β1和β2是K∞类函数.令V(η)=V1(z1)+U(w),且z1(0)∈Z1.如果以下不等式成立

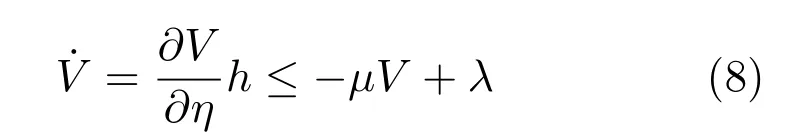
那么,w 有界并且z1 ∈Z1,∀t ∈[0,∞).

注3.由引理2 可得,对于∀t ＞0,只要|z1(0)|＜kj,d1,则有|z1(t)|＜kj,d1.又因为yj=zj,1+yr,而假设2 给出期望信号yr有界且上界为Y0,因此,只要令kj,d1+Y0=kc1,则保证系统输出yj的约束永不被违反.所以,我们得出结论:输出约束控制是一种间接约束,即通过对跟踪误差进行约束继而达到输出约束的目的.

引理3[20].对任意正常数kj,d1,且满足|zj,1|＜kj,d1,有如下不等式成立

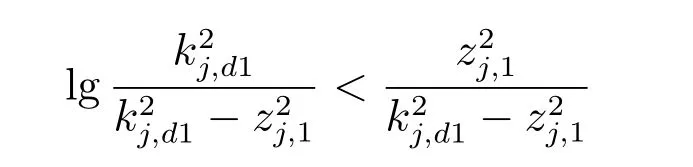
引理4[21].对任意变量z和任意常数ξ ＞0,有如下不等式成立

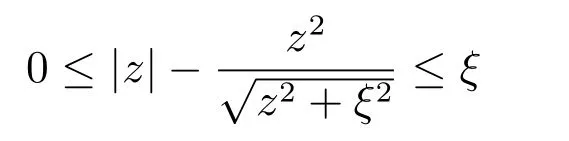
1.2 径向基函数神经网络(RBFNN)

对于任意连续函数f(Z):Rq→R,利用径向基函数神经网络(Radial function neural network,RBFNN)估计,得到如下表达式

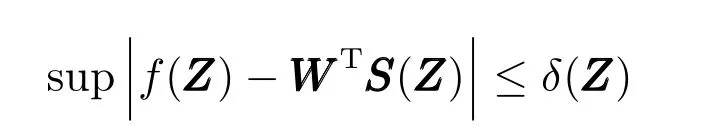
其中,WWW ∈Rl为权向量,l ＞1 为神经网络节点个数,Z ∈ΩZ⊂Rq为输入向量,SSS(Z)=[s1(Z),s2(Z),···,sl(Z)]T∈Rl为高斯基函数向量,定义为

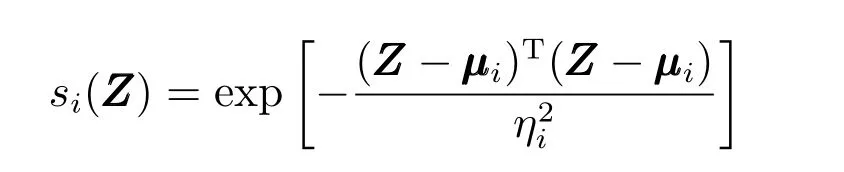
其中,i=1,2,···,l,μi和ηi分别为高斯基函数的中心和宽度.

文献[22] 研究表明,神经网络能够在有界闭集ΩZ⊂Rq上以任意精度逼近任意连续函数f(Z):

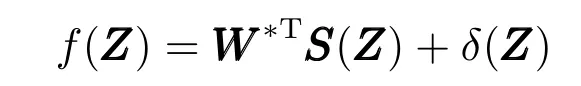
其中,WWW*为理想权值向量,δ(Z)为逼近误差,满足

本文控制目标是对于每一个子系统,设计自适应量化跟踪控制器使得闭环系统所有信号最终一致有界,而且保证跟踪误差收敛到原点的一个小邻域,同时,所有子系统输出都不违反约束条件.

2 自适应分散跟踪控制设计

2.1 量化参数δj和uj,min已知

本小节讨论当量化参数均为已知情况下,基于反推法设计输出约束的自适应分散量化控制策略.对于第j 个子系统,反推法设计过程一共包含n步,在最后一步设计中,我们给出实际控制输入uj.

互联项相关参数定义为

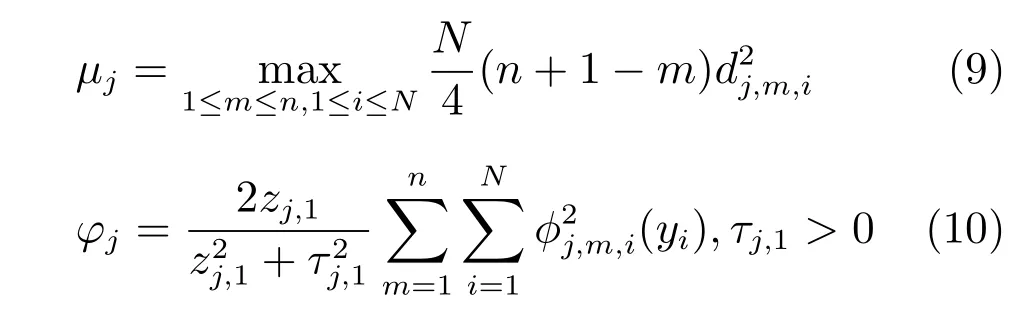
对子系统j,定义如下坐标变换表达式

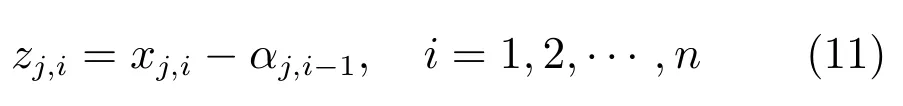
其中,αj,0=yr(t),αj,i为第i步设计的虚拟控制器.

利用自适应反推控制技术为系统(1)进行控制设计.整个设计过程包括n步.

第1步选取虚拟控制律αj,1以及参数和的自适应律为

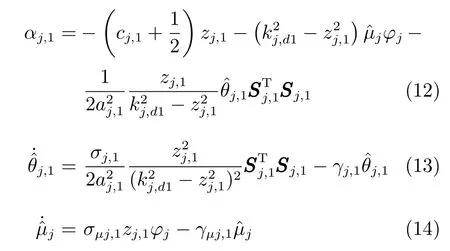
第2步选取虚拟控制律αj,2和参数的自适应律为

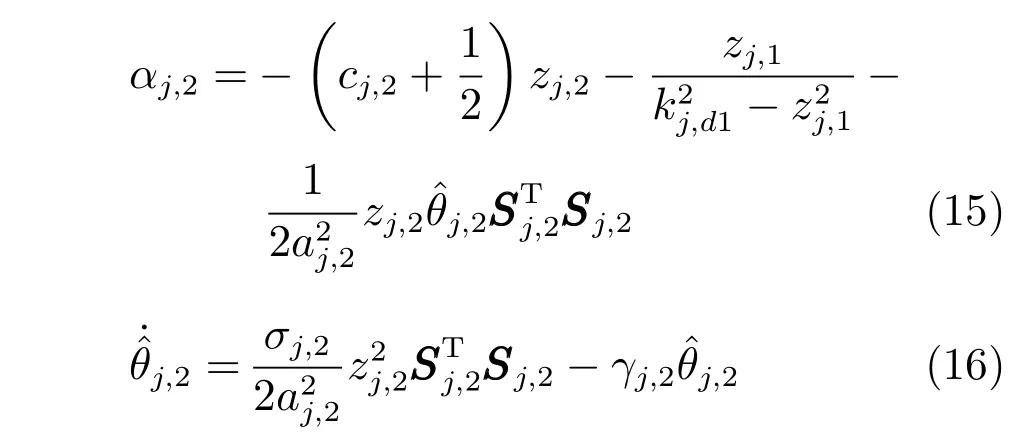
第k (3≤k ≤n-1)步选取虚拟控制律αj,k和参数的自适应律为

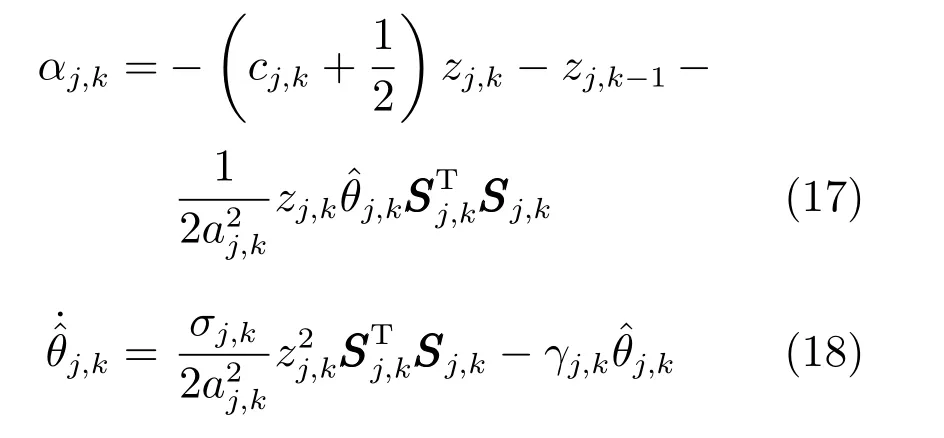
第n步设计实际控制律uj和参数的自适应律为

下面给出具体的控制设计过程.

第1步.由式(1)和式(11)对zj,1求导得到

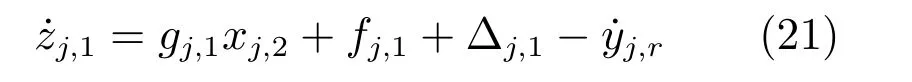
定义障碍李雅普诺夫候选函数

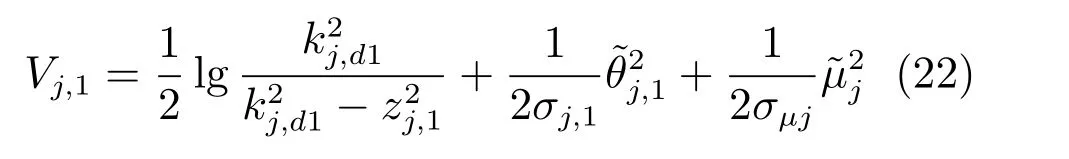
其中,kj,d1是zj,1的约束条件,即|zj,1|≤kj,d1.

根据式(1),式(11)和式(21),得到

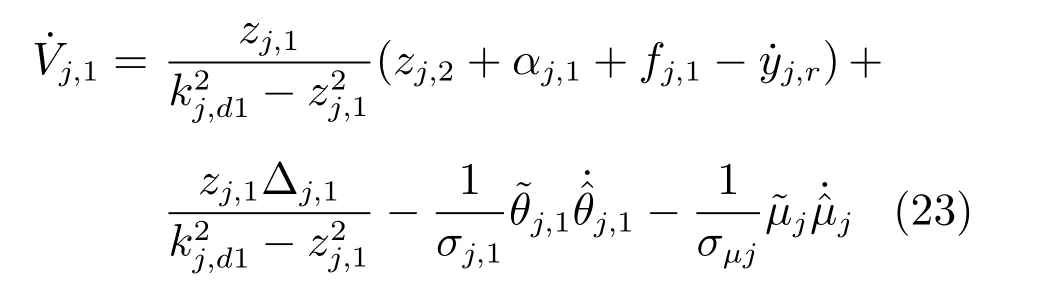
根据式(3)和Young′s不等式,可得

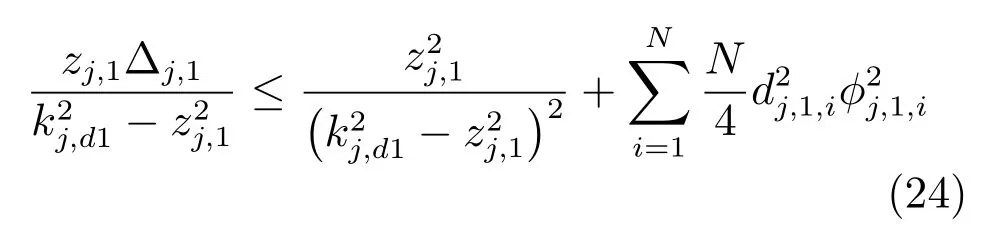
将式(24)代入式(23),得到

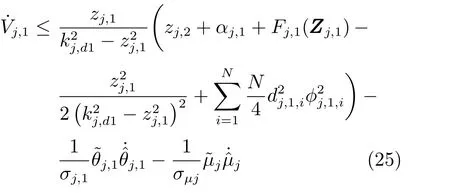
由于fj,1是未知光滑函数,所以不能直接利用Fj,1(Zj,1)来构造虚拟控制器,根据径向基函数神经网络的万能逼近特性,对存在使得

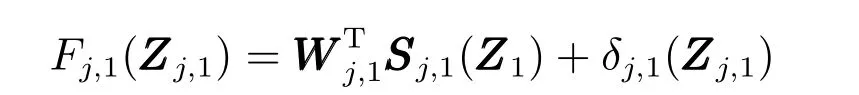
利用配方法,根据Young′s 不等式,对于给定的常数aj,1＞0,有如下不等式成立

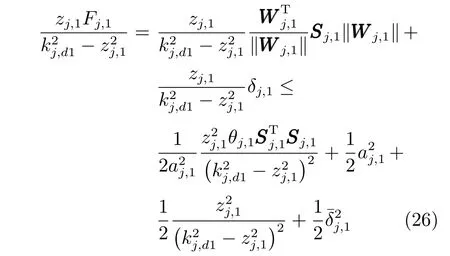
将式(26)代入式(25),得到

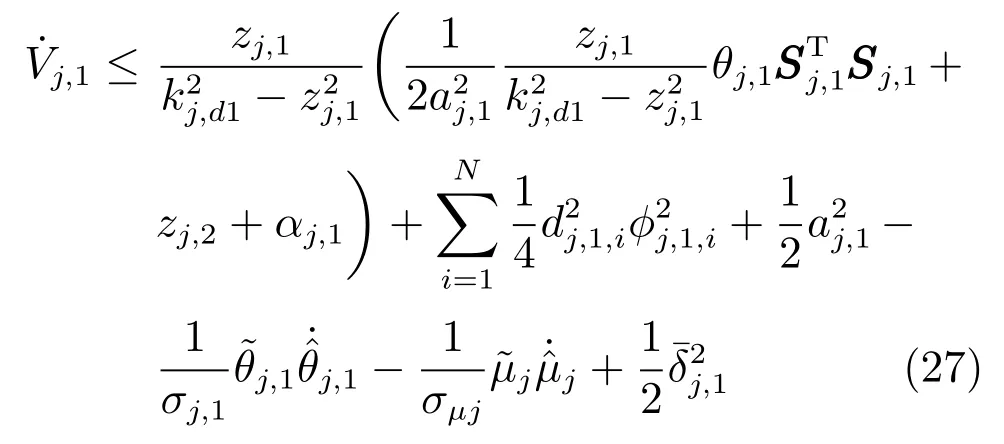
构建虚拟控制律αj,1(式(12))以及参数和的自适应律(式(13)和式(14)),则式(27)可简化为

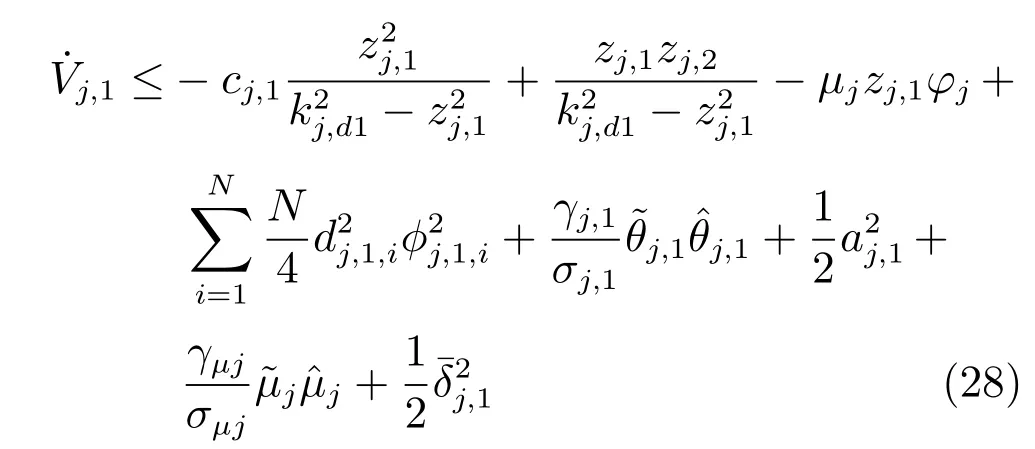
第2 步.根据式(1)和式(11),对zj,2求导得

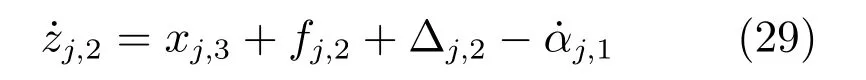
定义李雅普诺夫候选函数

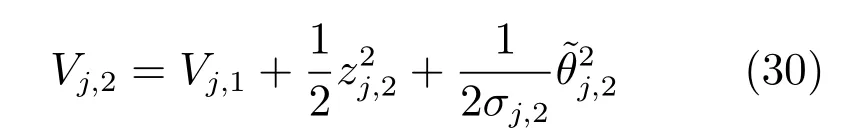
将Vj,2对时间t 求导,得到

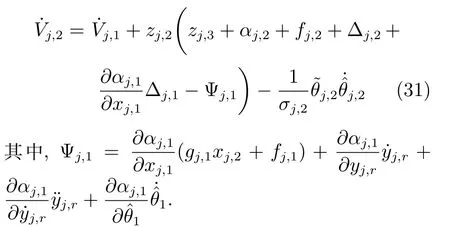
根据假设1和Young′s 不等式,得到

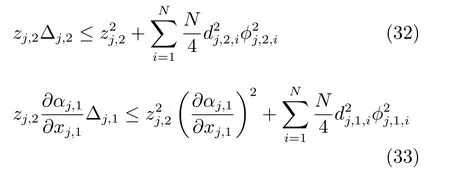
将式(32)和式(33)代入式(31),得到

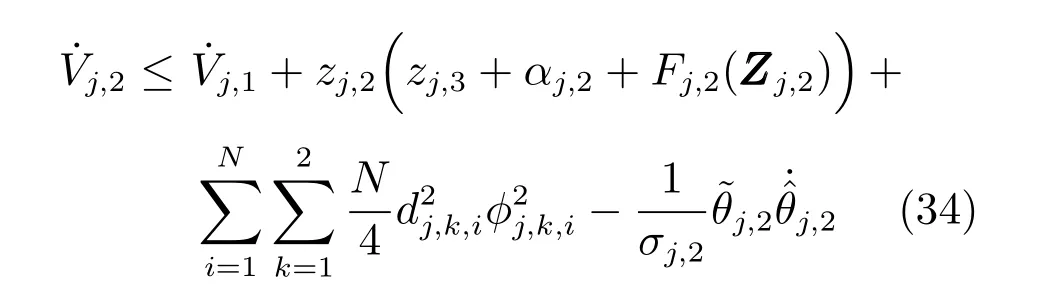
其中

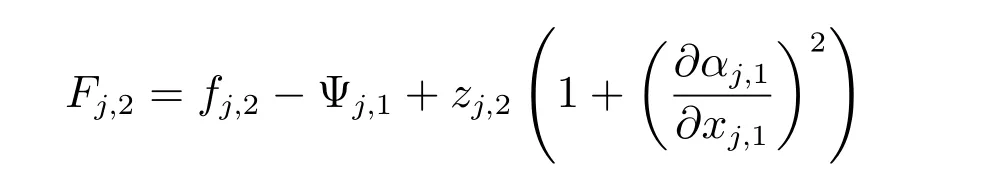
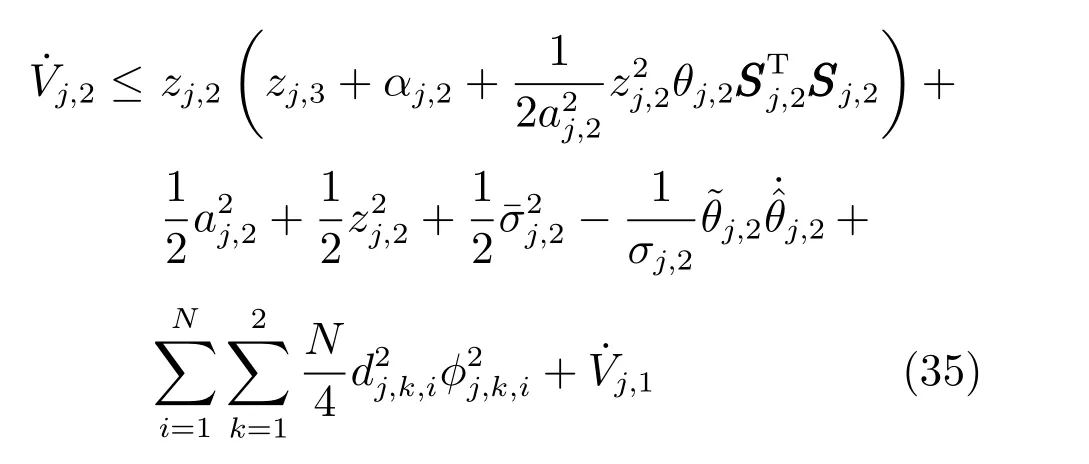
构建虚拟控制律αj,2(式(15))以及参数自适应律(式(16)),则式(35)可简化为

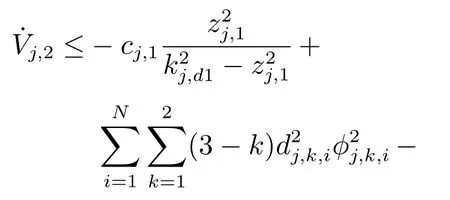
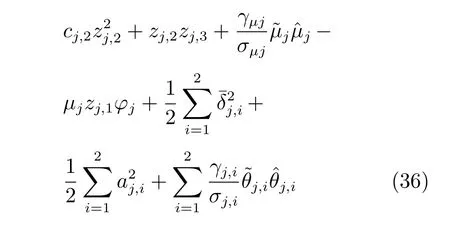
第k 步(3 ≤k ≤n-1).根据式(1)和式(11),对zj,k求导得

定义李雅普诺夫候选函数

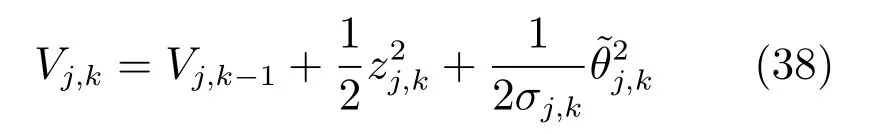
将Vj,k对时间t 求导,代入式(37),得到

其中,

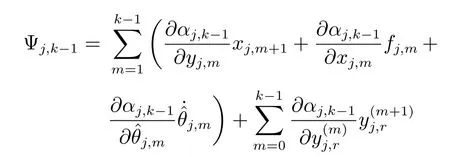
类似第2 步中式(32)～(34)的处理过程,可得未知非线性函数

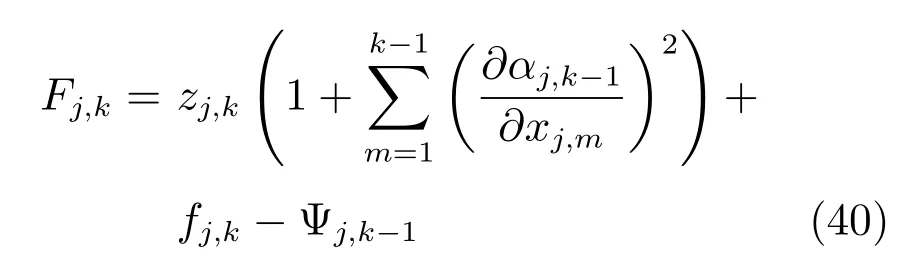
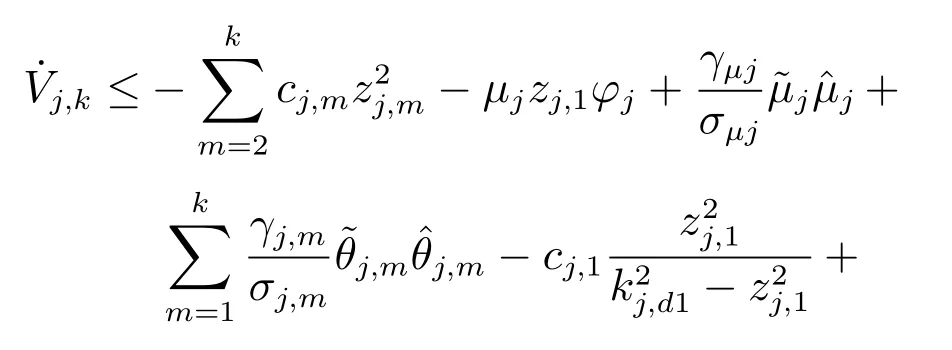
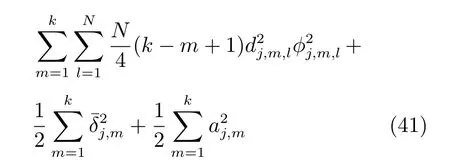
第nnn 步.根据式(1)和式(11),对zj,n求导得

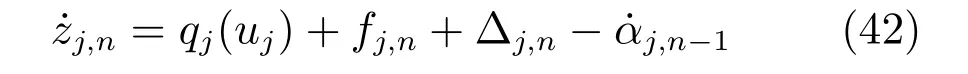
定义李雅普诺夫候选函数

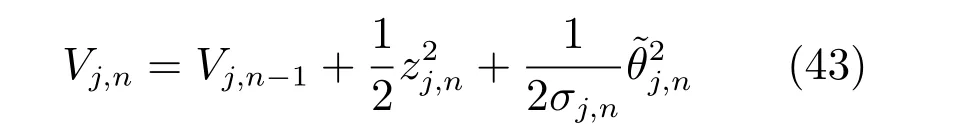
根据式(42),将Vj,n对时间t 求导,得到

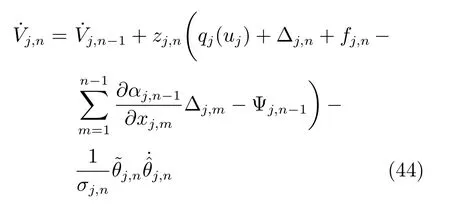
其中,

应用与第k 步类似的处理过程,得到

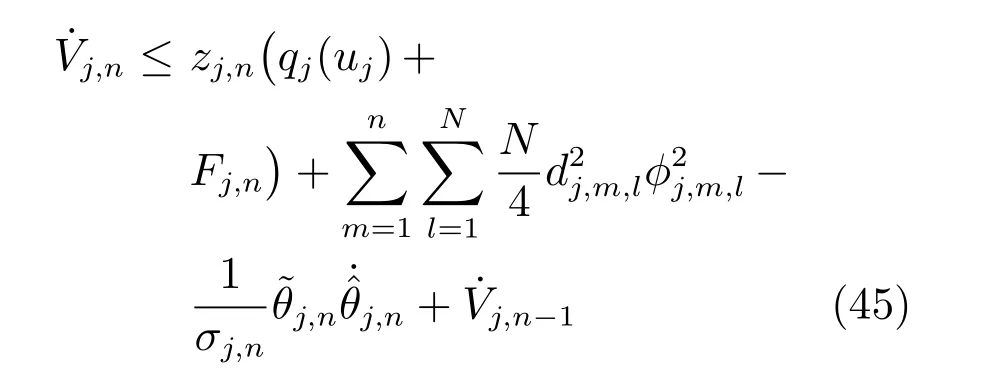
其中,Fj,n的形式为k=n 时的式(40).类似第1步的处理过程,利用径向基函数神经网络逼近未知函数Fj,n,并构建实际控制律uj(式(19))以及参数自适应律(式(20)),则式(45)可简化为

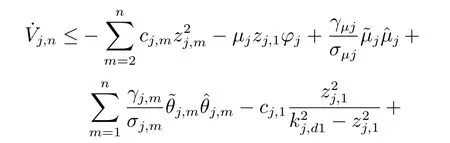
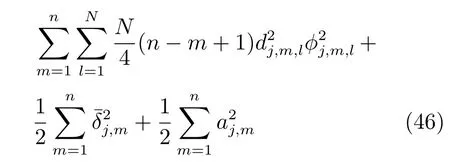
至此,整个自适应量化跟踪控制设计完成.下面以定理形式给出本文主要结果.

定理1.考虑具有输入量化和输出受限的非线性互联系统(1),满足假设1和假设2,设计虚拟控制器(12),(15),(17)和实际控制器(19),以及参数自适应律(13),(14),(16),(18)和(20),则对于任意的有界初始条件和ˆθj,k(0)＞0,闭环系统所有信号最终一致有界,并且存在有限时间T,使得当t ＞T时,子系统的输出跟踪误差收敛到有界闭集Ω1中

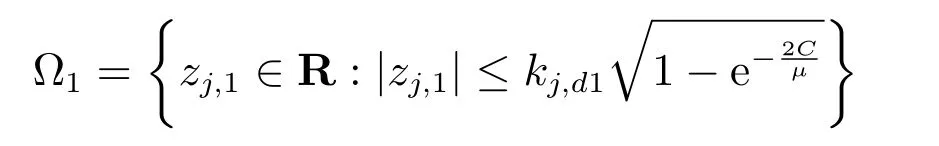
证明.对互联系统整体选取李雅普诺夫函数

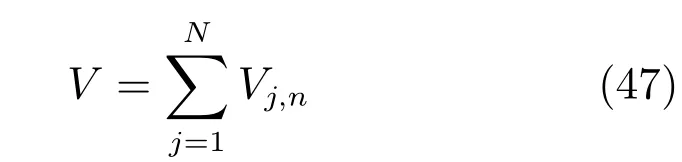
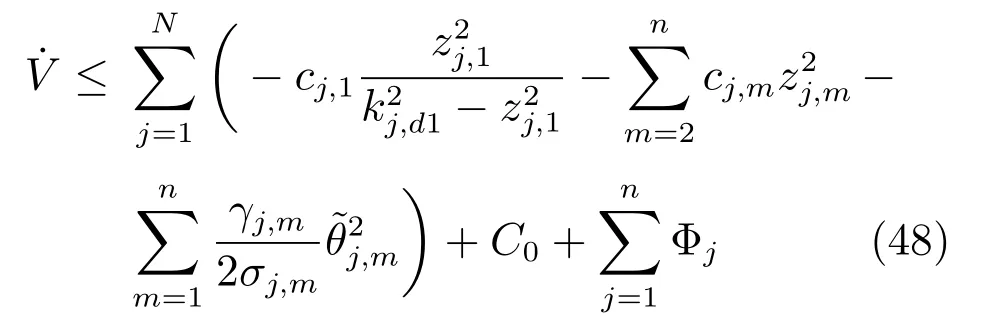
其中,

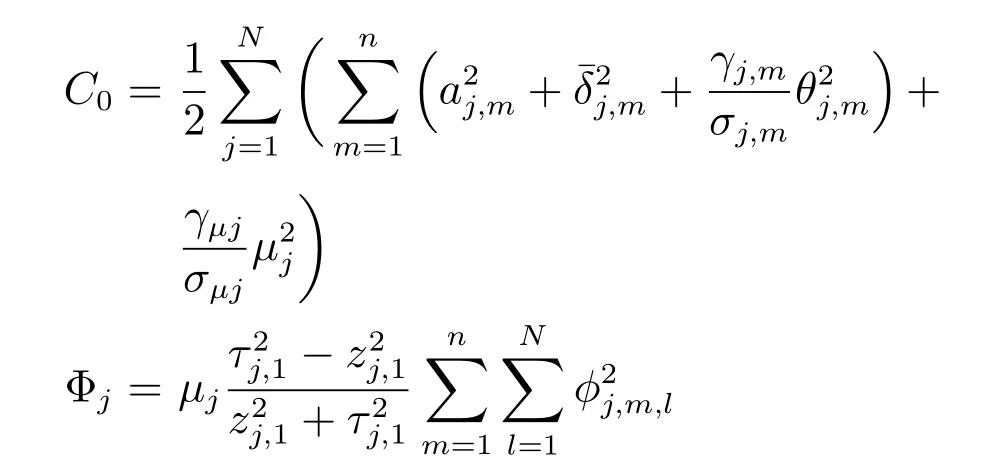
当|zj,1|≥τj,1时,Φj≤0;当|zj,1|＜τj,1时,Φj＞0,且有上界

由引理2 可得

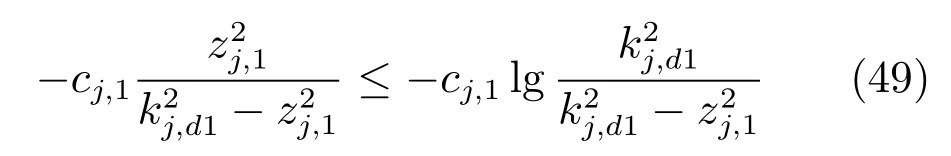
因此,由以上分析可得

对式(50)两边积分得到

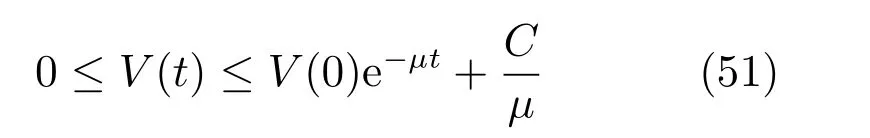
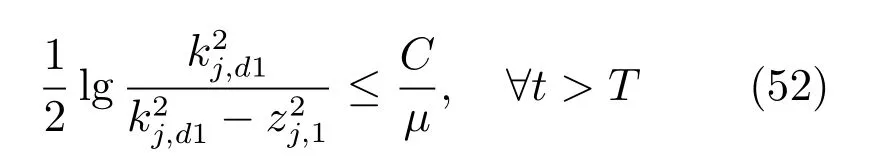
对式(52)两边取e 指数,可得

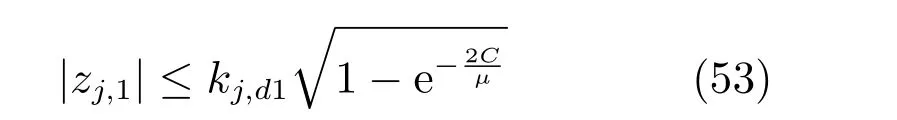
式(51)表明V 是有界的,由V 的定义可得误差信号zj,1,有界,αj,i是关于zj,1和的函数,故有界,且|zj,1|≤kj,d1.由于yj=yr+zj,1,利用假设2 容易推出|yj|≤|yr|+|zj,1|＜Y0+kj,d1=kc1.因此闭环系统所有信号有界,输出满足约束条件,且跟踪误差最终收敛到有界闭集Ω1. □

2.2 量化参数δj,uj,min 未知

本节考虑当量化参数δj和uj,min未知时的控制设计.量化参数未知的量化跟踪控制设计是极具挑战性的难题,目前极少量文献涉及到此类问题.文献[11] 主要利用双曲正切函数的特性对控制信号进行转换,从而给出问题解决方案.本节我们讨论另一种新的解决方法.鉴于自适应反推设计的前n-1 步与第2.1 节完全相同,所以我们重点讨论第n 步设计过程.

首先,定义新的变量

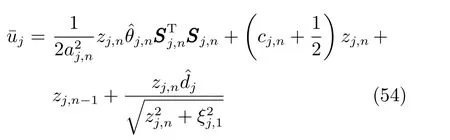
设计系统实际控制输入uj为

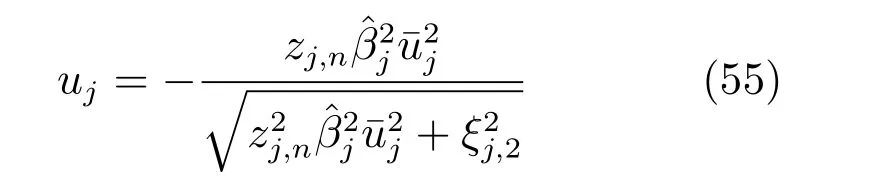
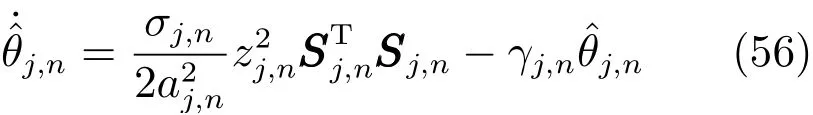
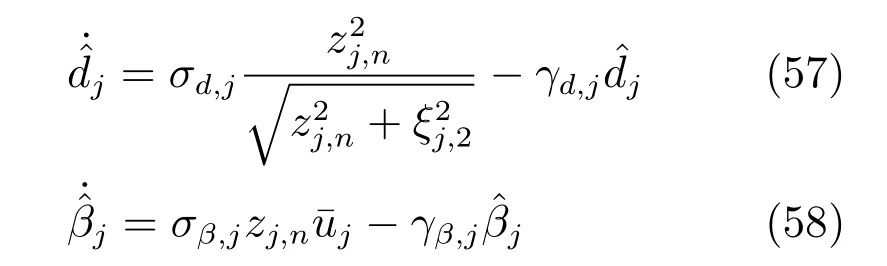
定义李雅普诺夫候选函数

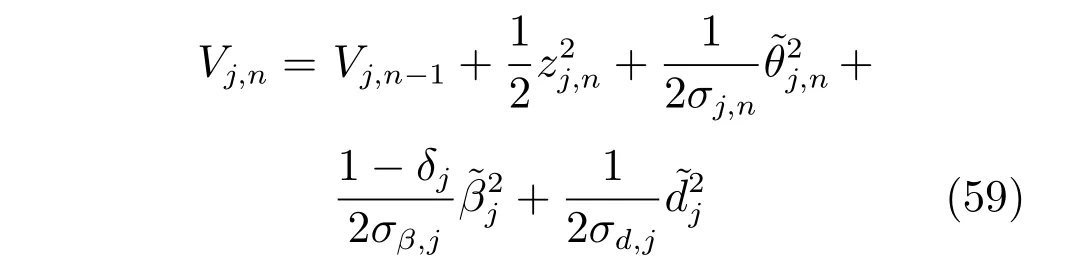
对式(59)求导得到

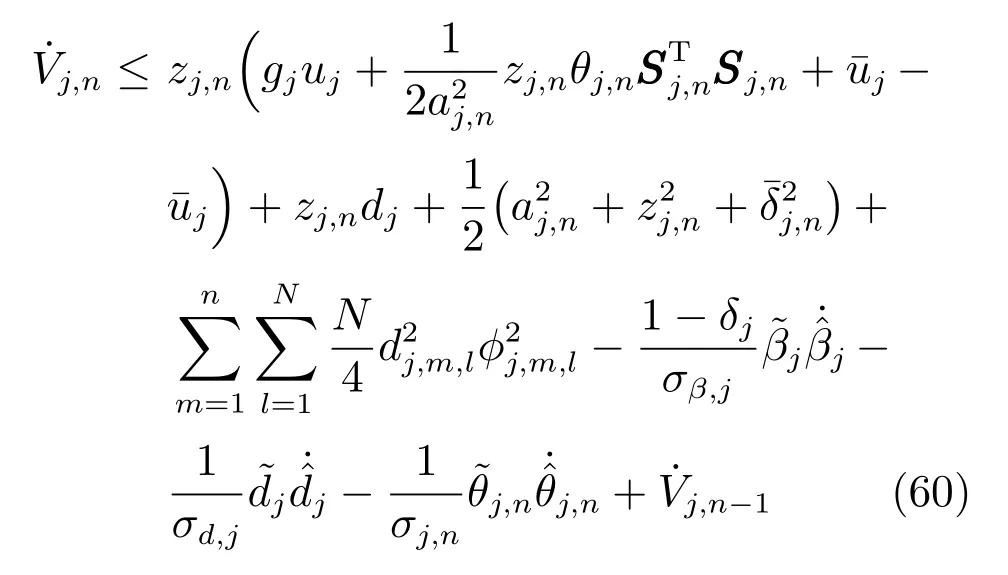
由式(54)和引理3,可得

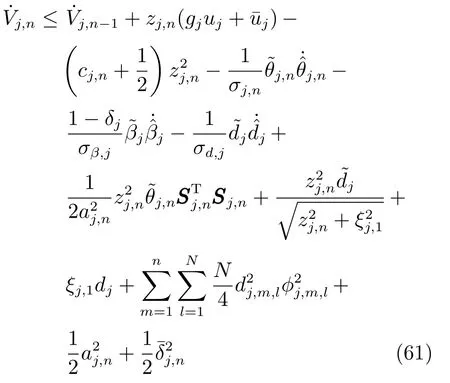
由于gj≥1-δj,有如下不等式成立

将式(62)代入式(61),得到

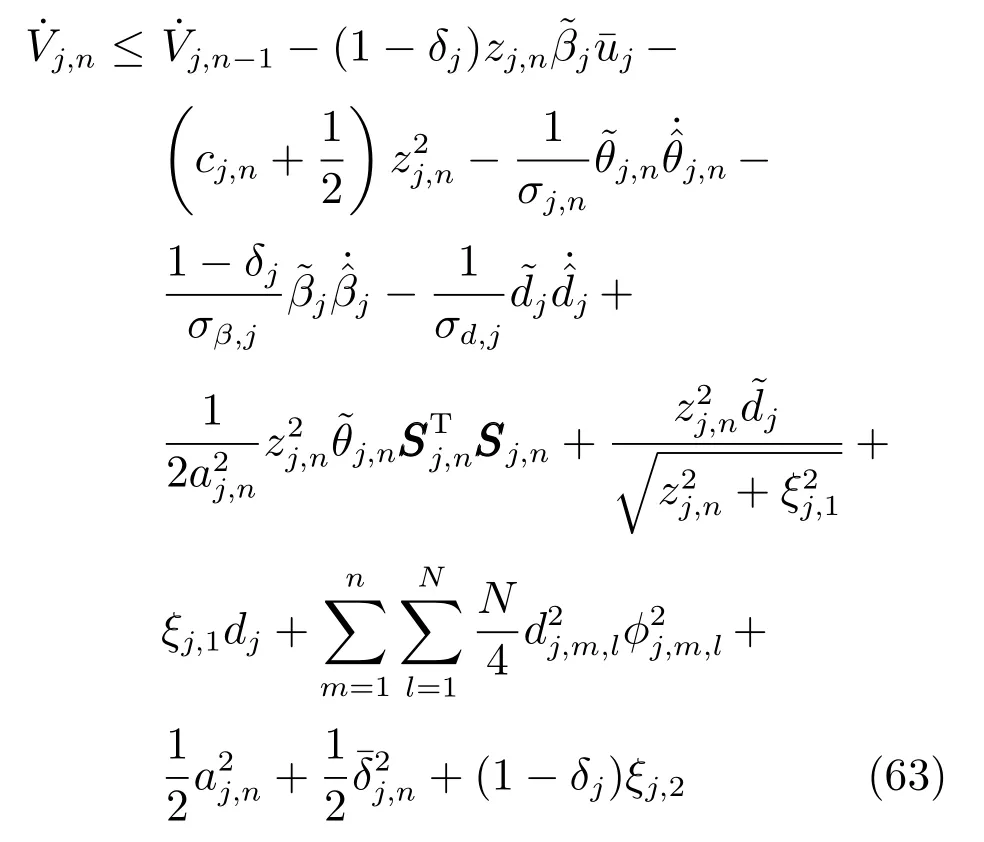
注3.由于直接利用量化输入qj(uj)进行控制器设计极具挑战性,因此借助引理1 将其进行转换分解,但同时产生了新的动态控制系数gj(uj).为了克服这一动态系数导致的自适应设计困难,我们将动态系数转换为其下界1-δj,通过进一步变换处理,如式(62),从而解决了输入量化带来的设计困难.

注4.基于输入量化的变换处理,这里我们对未知量化参数的估计不是量化参数本身,而是其相关表达式βj和dj,βj=1/(1-δj),dj≥uj,min.

定理2.针对带有输入量化和输出受限的非线性互联系统(1),满足假设1和假设2,设计虚拟控制器(12),(15),(17),实际控制器(55),以及参数自适应律(13),(14),(16),(18),(56)～(58),则对于任意的有界初始条件和ˆθj,k(0)＞0,闭环系统所有信号一致有界,并且存在有限时间T,使得当t ＞T时,子系统的输出跟踪误差收敛到有界闭集Ω1中

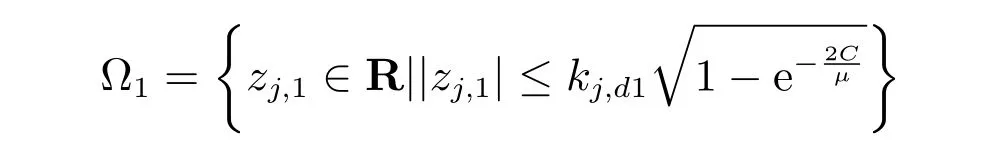
证明.对互联系统整体选取李雅普诺夫函数

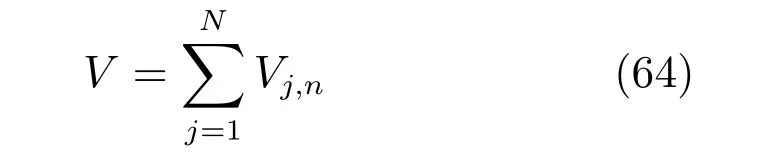
类似定理1 证明过程,得到如下不等式

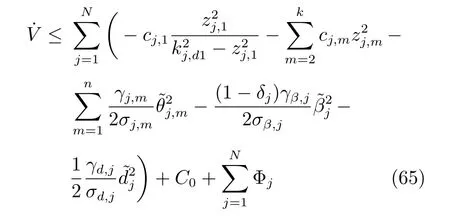
其中,

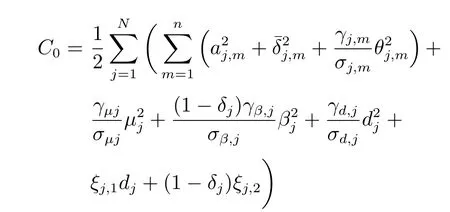
因此,

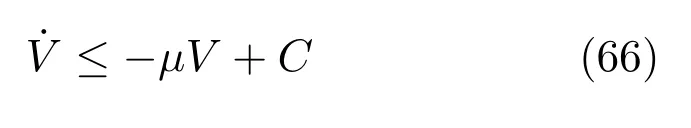
其中,

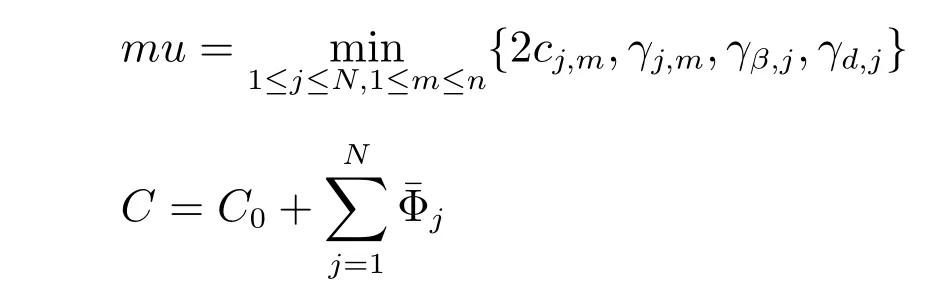
从而得到

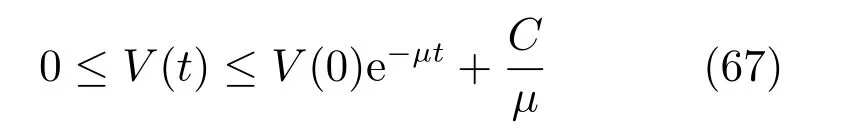
同定理1 的分析,得出结论:闭环系统所有信号一致有界,跟踪误差最终收敛到有界闭集Ω1,且满足输出约束条件. □

3 仿真

为验证所提控制方案的有效性,本节考虑如图1所示由弹簧连接的互联三倒立摆系统的跟踪控制问题,假设三个倒立摆之间的未知关联由弹簧连接,每个倒立摆系统由各自的伺服电机进行驱动,即ui(i=1,2,3)进行控制,倒立摆的动力学模型为[23]

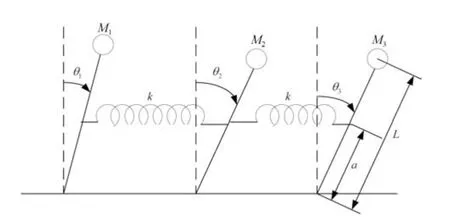
图1 三重倒立摆示意图Fig.1 Schematic of tripled inverted pendulums

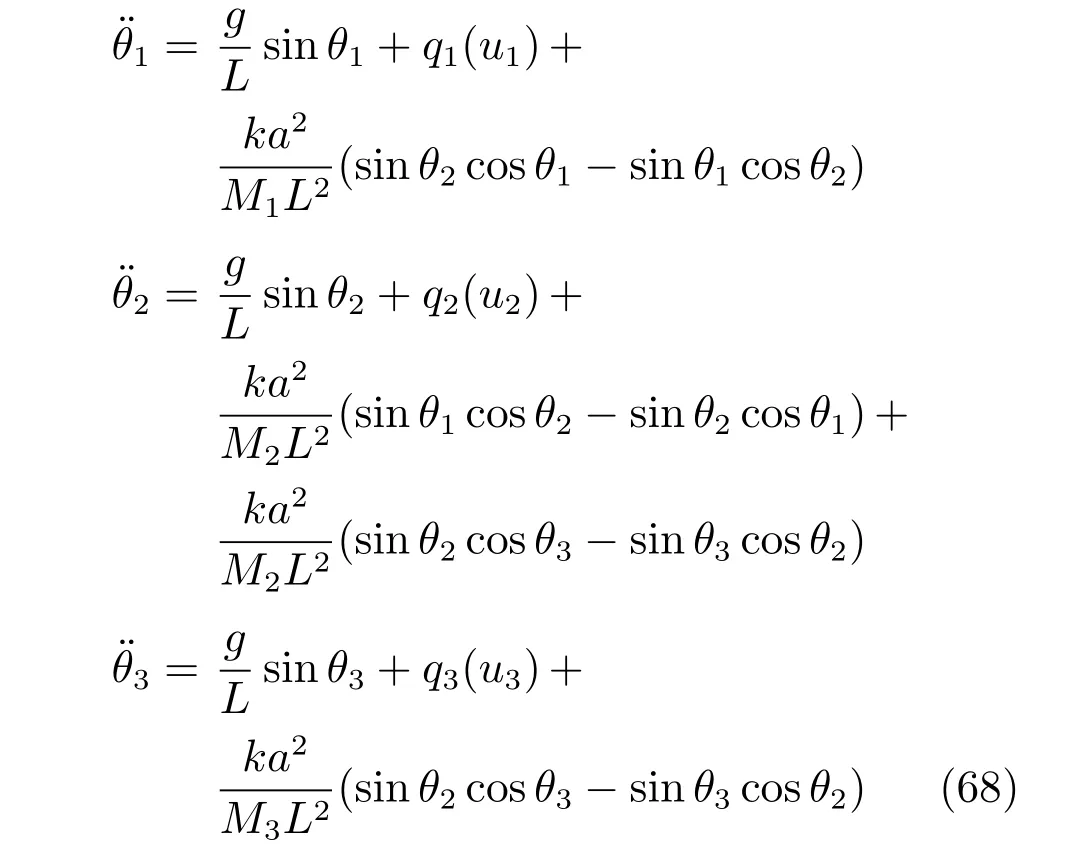
其中,θ1,θ2和θ3为摆角,g 为重力加速度,M1和M2为摆的质量,L 为摆杆长度,k 为弹簧的弹性系数,a 为从弹簧连接点到摆的支点的距离.

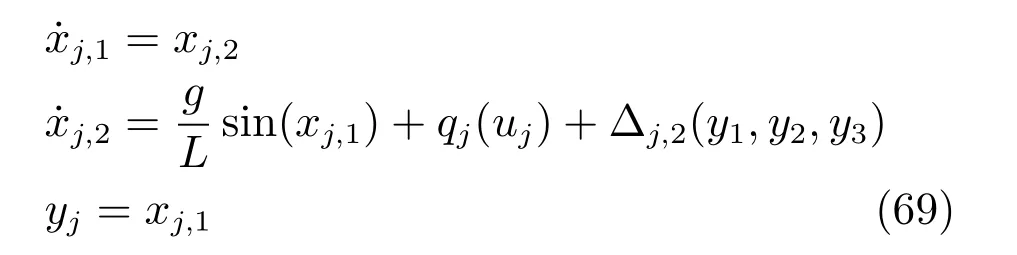
其中,qj(uj)为量化输入,其表达式如式(2),yj为系统输出,互联项为Δ1,2=(ka2/M1L2)sin(y2-y1),Δ2,2=(ka2/M2L2)（sin(y1-y2)+sin(y2-y3)）,Δ3,2=(ka2/M2L2)sin(y2-y3).约束上界选取k1,d1=k2,d1=k3,d1=0.1,参考输出为y1,r(t)=1-cos(t),y2,r(t)=sin(t),y3,r(t)=0.5 sin(t).

系统参数为:M1=1.5 kg,M2=1.6 kg,M3=1.5 kg,L=0.5 m,g=9.81 m/s2,r=80 N/m,a=0.2 m.

情况1.根据定理1,虚拟控制、参数自适应律和实际控制分别为

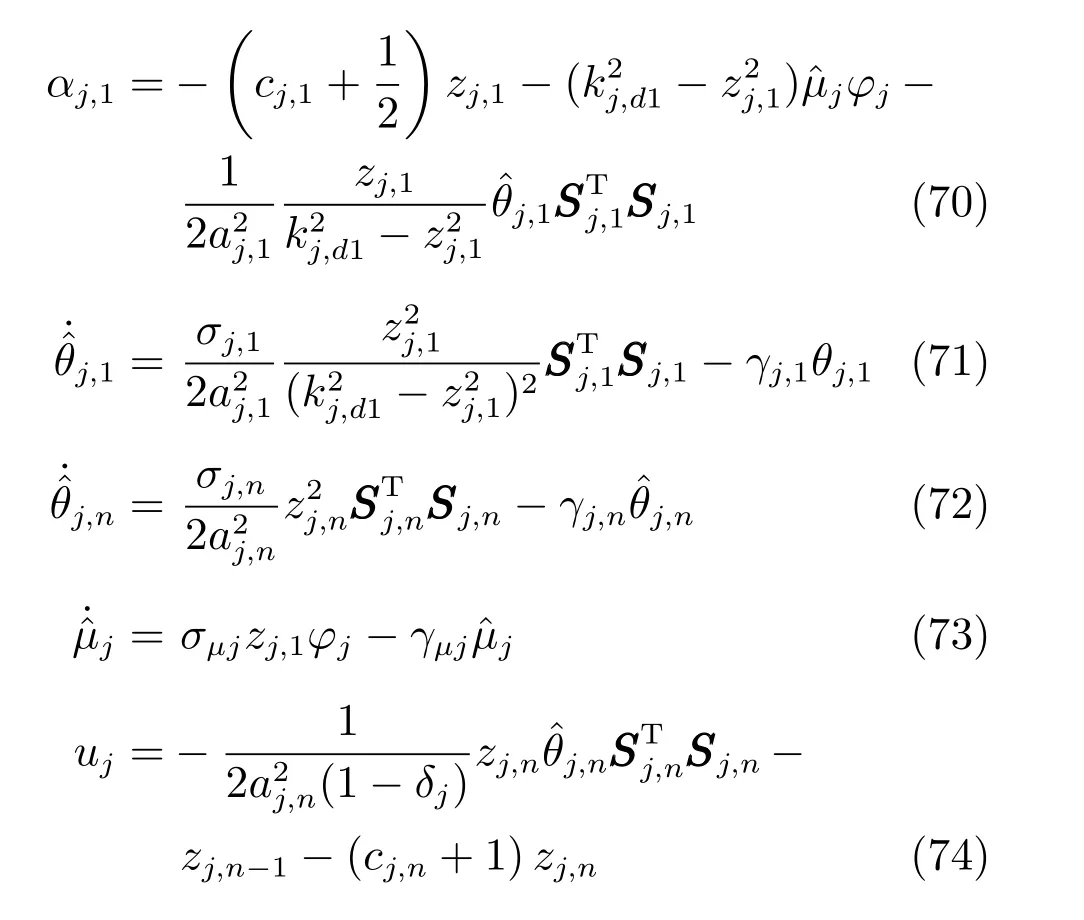
初始值选取为

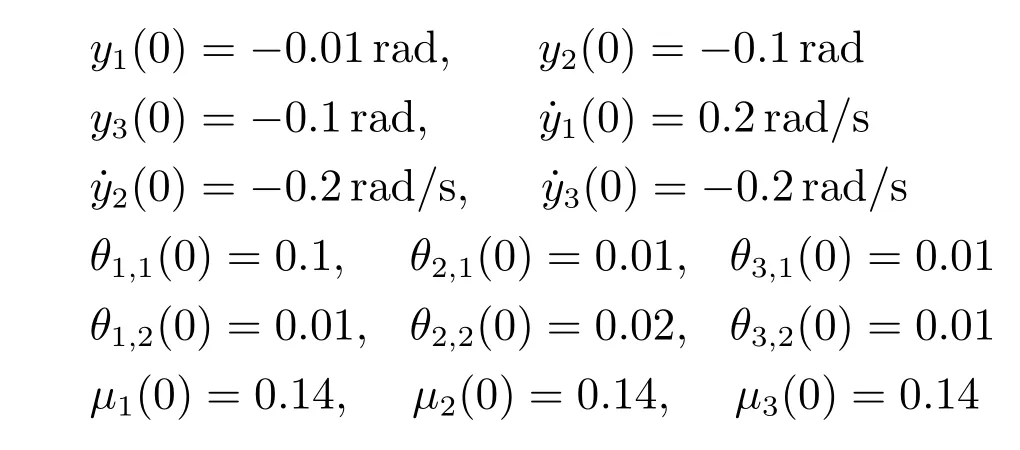
设计参数选取为

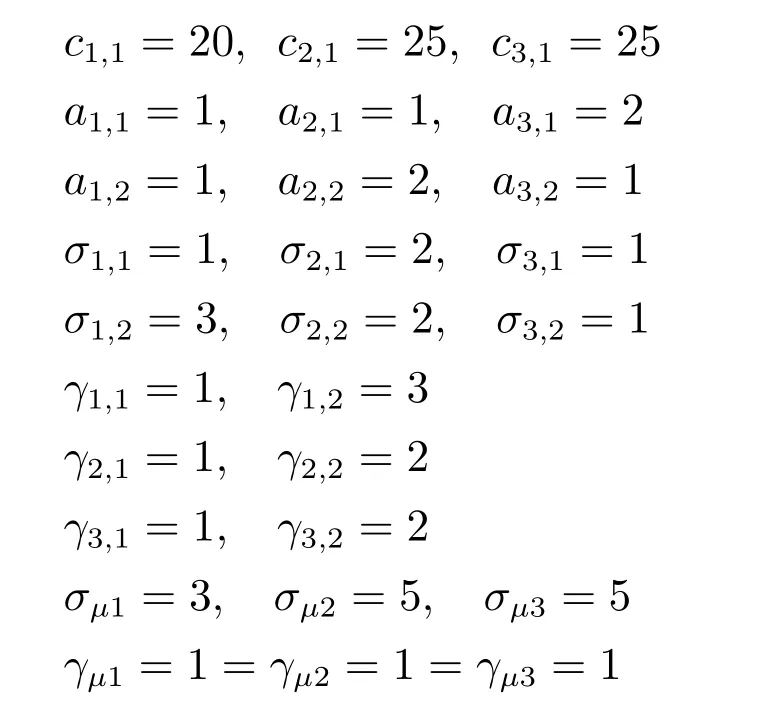
量化参数选取为

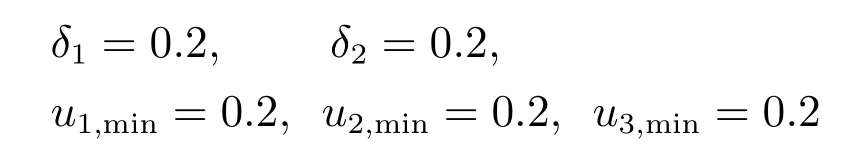
高斯隶属度函数选取为

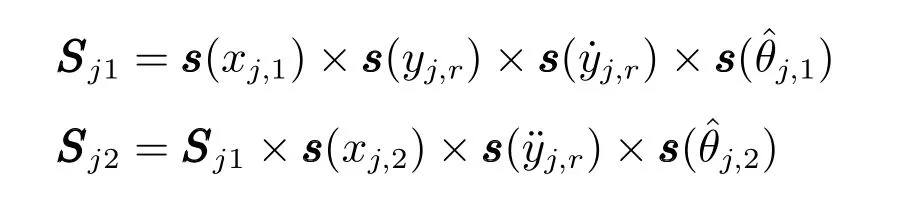
选取dj,2,1=dj,2,2=ra2/(MjL2),φj,2,1=,则假设1 成立.

情况2.根据定理2,参数dj和βj自适应律和实际控制器uj分别设计如下,其余同情况1.

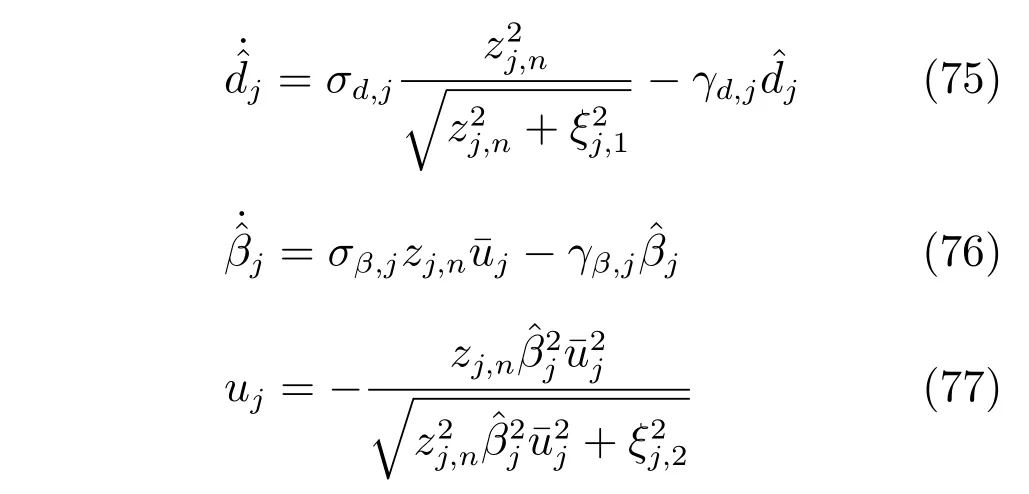
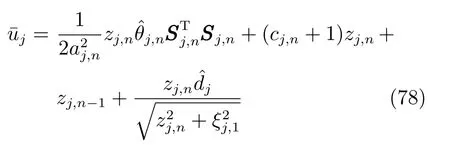
设计参数选取为

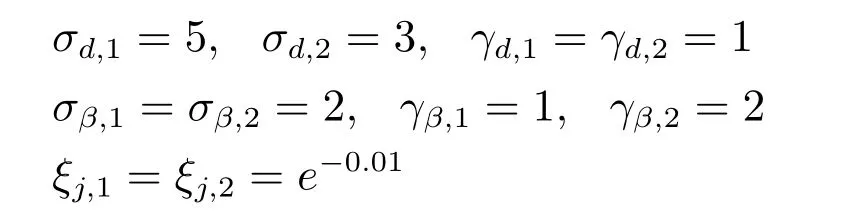
其余参数选取同情况1.

注5.文献[11] 所设计虚拟控制器表达式要求互联强度为已知常数.本文的设计方法不要求互联强度已知,而是通过估计未知互联常数表达式上界(10)来设计虚拟控制器,因此,与文献[11] 相比,本文的设计方法更具一般性.

仿真结果如图2～16 所示.图1～10 分别为量化参数已知的情况下,系统输出轨迹,跟踪误差轨迹和控制输入信号以及量化信号的轨迹.图11～16分别为量化参数未知的情况下,系统输出轨迹,跟踪误差轨迹和控制输入信号以及量化信号的轨迹.仿真结果表明无论量化参数已知与否,本文所提算法都能保证输出能跟踪上期望的参考信号,并且跟踪误差有界,同时确保了系统输出满足约束条件.仿真结果验证了定理1和定理2 结论的合理性.

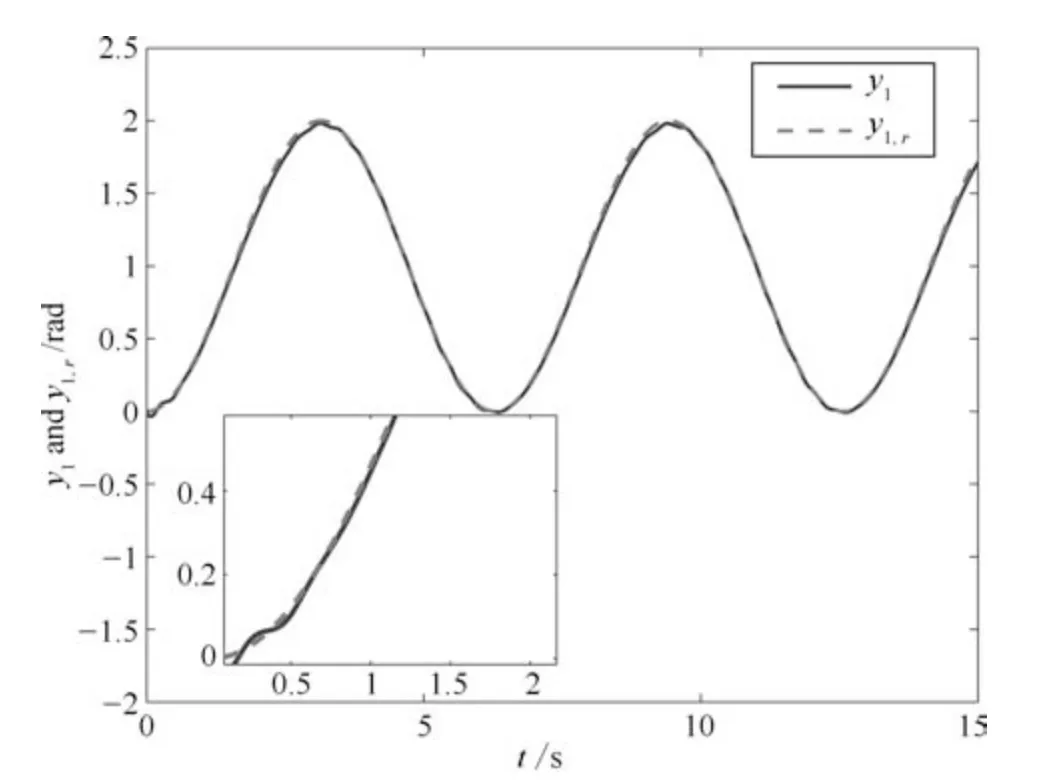
图2 输出y1和y1,r 的轨迹Fig.2 Trajectories of output y1 and y1,r

4 结论

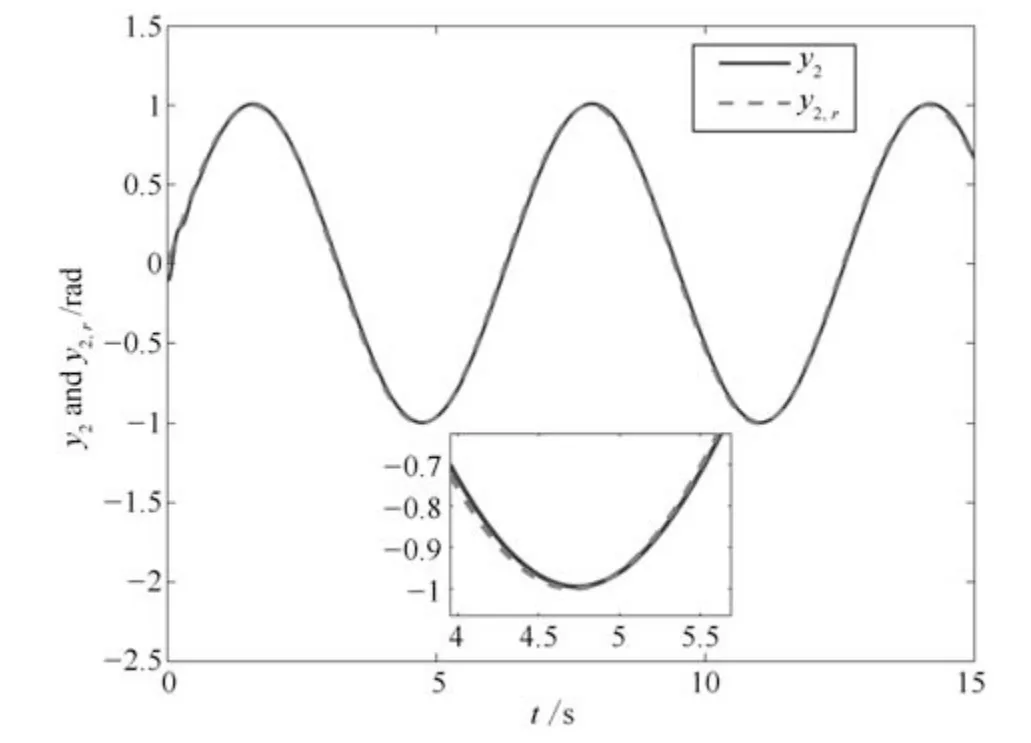
图3 输出y2和y2,r 的轨迹Fig.3 Trajectories of output y2 and y2,r

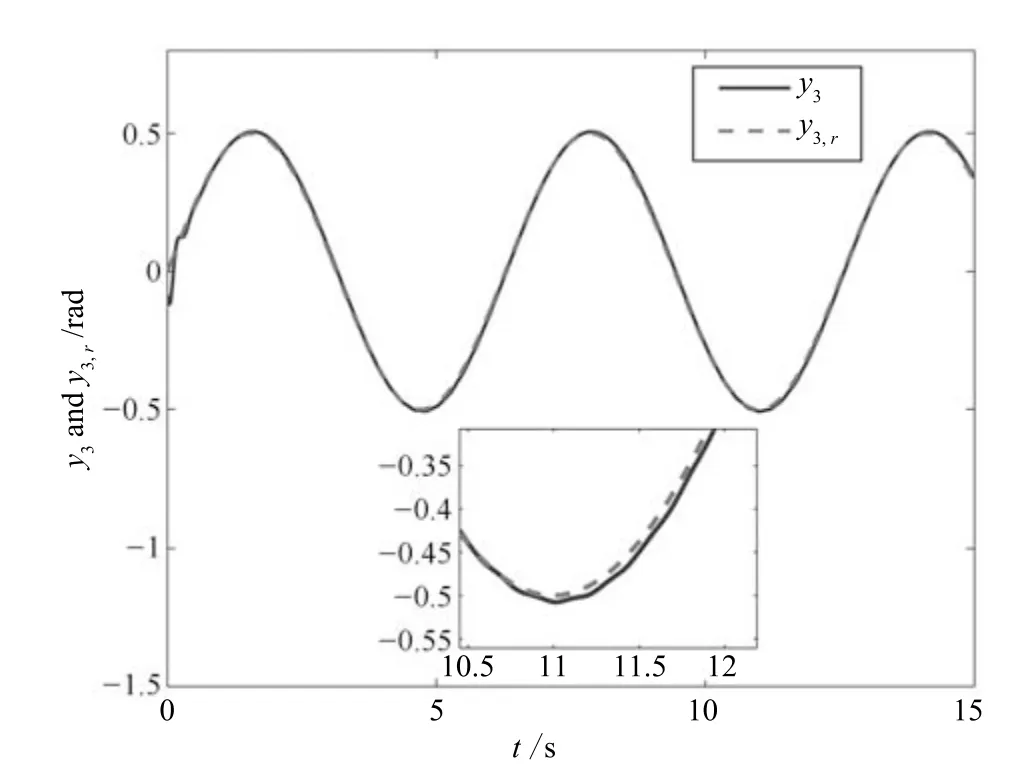
图4 输出y3和y3,r 的轨迹Fig.4 Trajectories of output y3 and y3,r

图5 量化参数已知时跟踪误差z1,1 的轨迹Fig.5 Trajectory of tracking error z1,1 with known quantization parameters

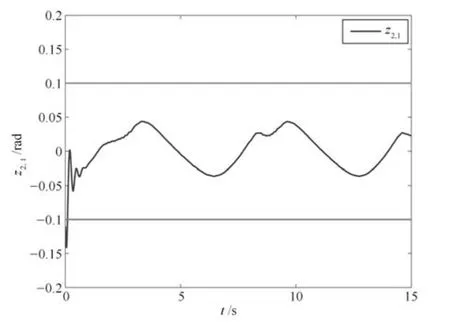
图6 量化参数已知时跟踪误差z2,1 的轨迹Fig.6 Trajectory of tracking error z2,1 with known quantization parameters

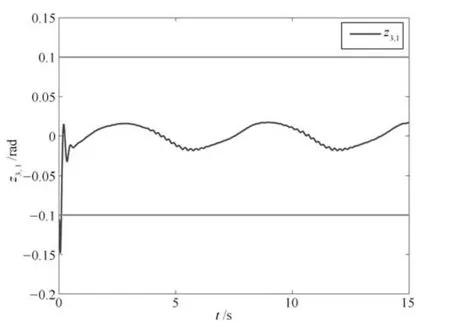
图7 量化参数已知时跟踪误差z3,1 的轨迹Fig.7 Trajectory of tracking error z3,1 with known quantization parameters

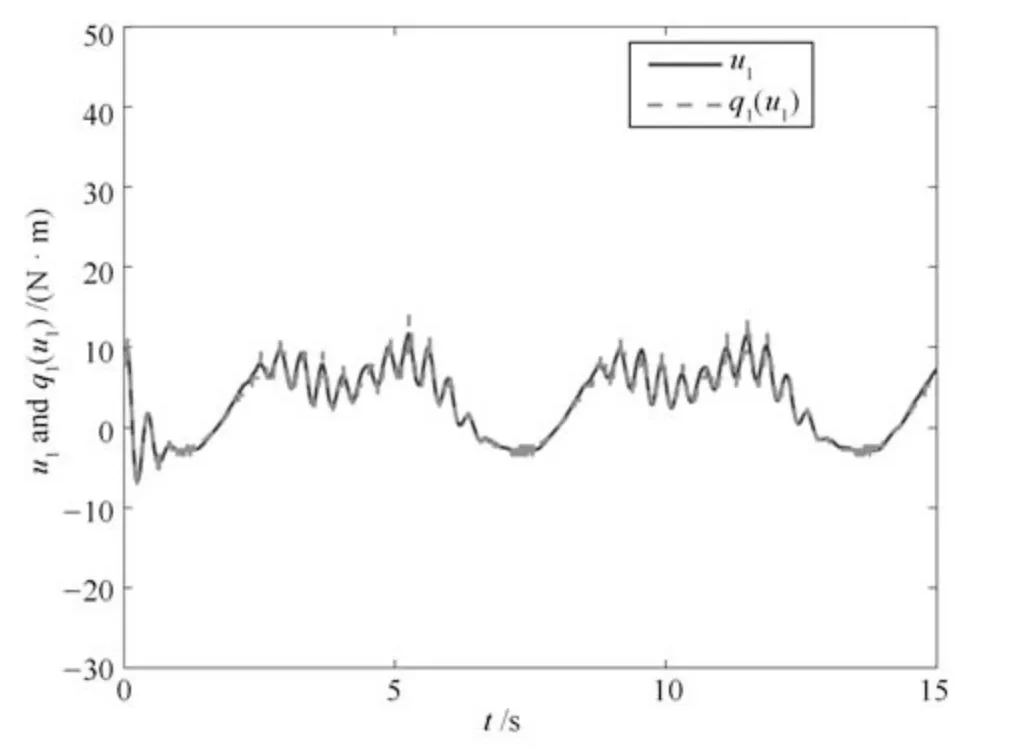
图8 量化参数已知时输入u1和q1(u1)的轨迹Fig.8 Trajectories of input u1 and q1(u1)with known quantization parameters

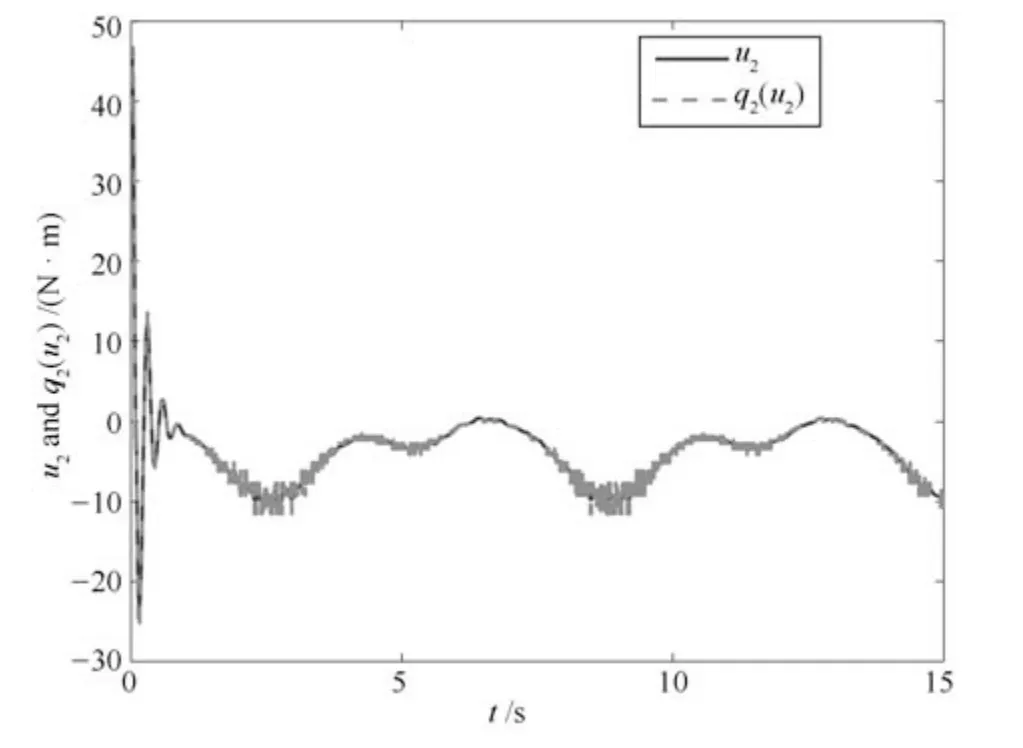
图9 量化参数已知时输入u2和q2(u2)的轨迹Fig.9 Trajectories of input u2 and q2(u2)with known quantization parameters

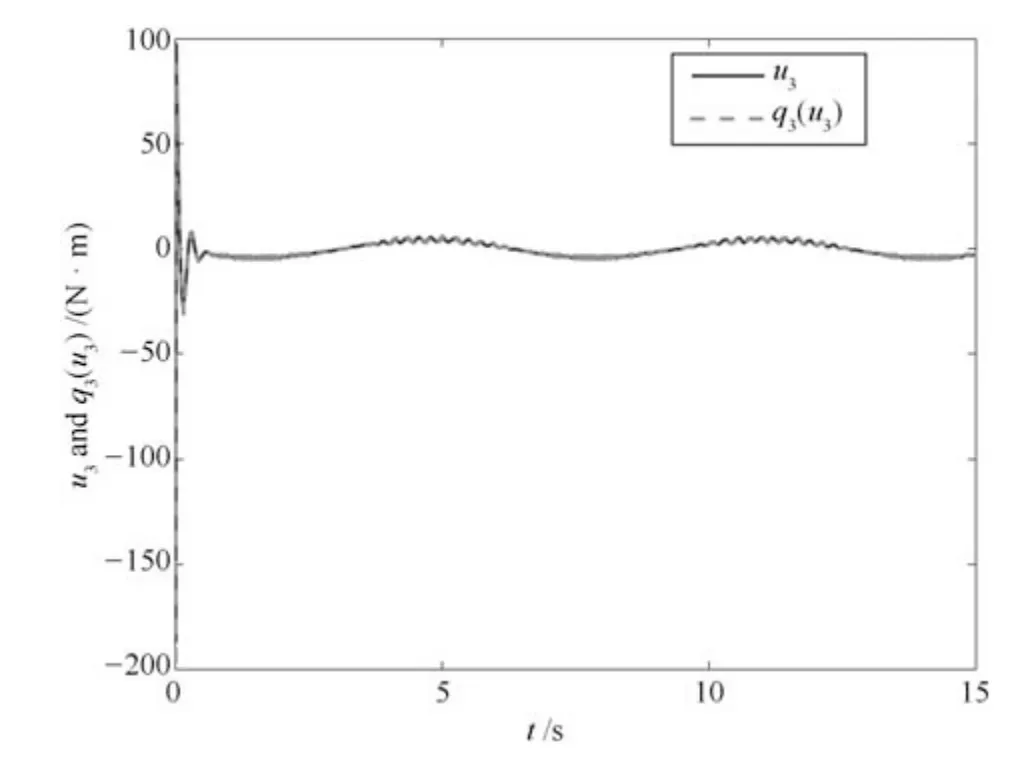
图10 量化参数已知时输入u3和q3(u3)的轨迹Fig.10 Trajectories of input u3 and q3(u3)with known quantization parameters

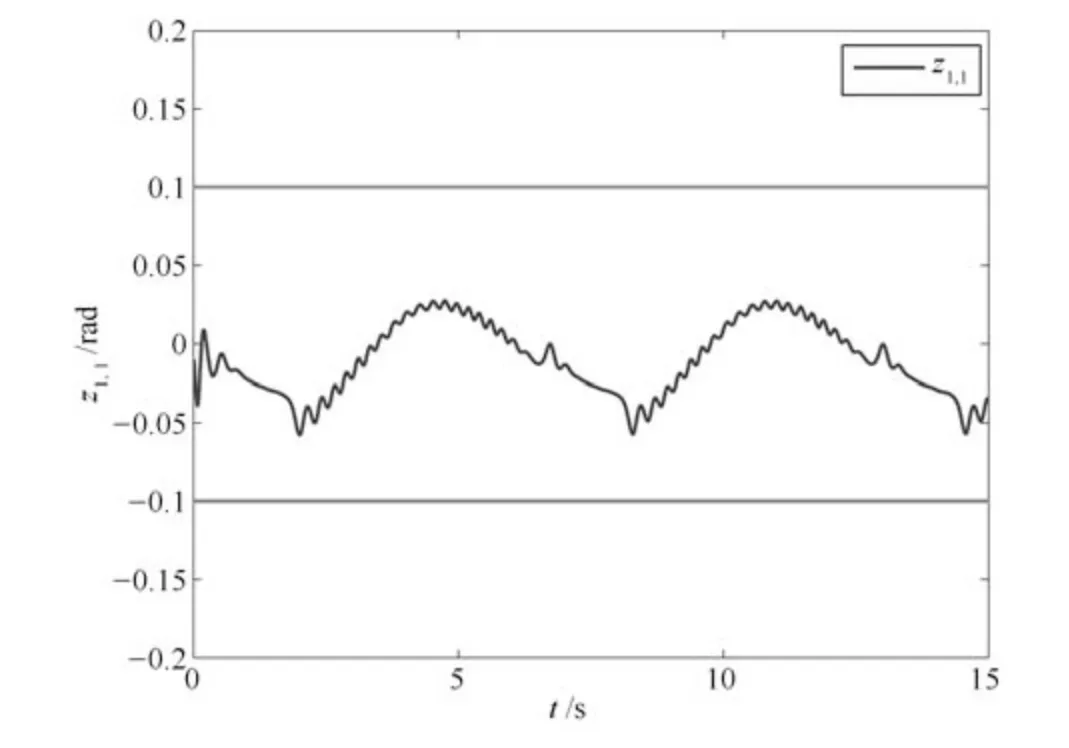
图11 量化参数未知时跟踪误差z1,1 的轨迹Fig.11 Trajectory of tracking error z1,1 with unknown quantization parameters

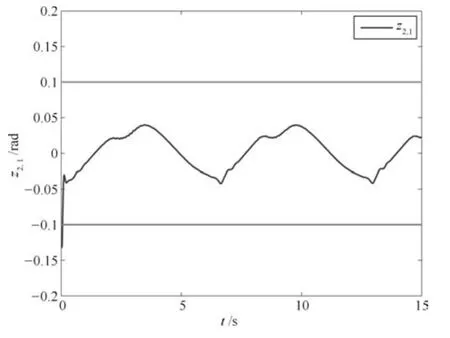
图12 量化参数未知时跟踪误差z2,1 的轨迹Fig.12 Trajectory of tracking error z2,1 with unknown quantization parameters

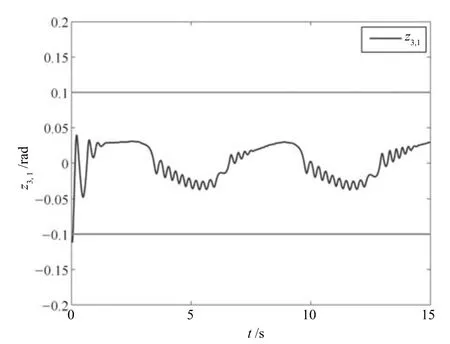
图13 量化参数未知时跟踪误差z3,1 的轨迹Fig.13 Trajectory of tracking error z3,1 with unknown quantization parameters

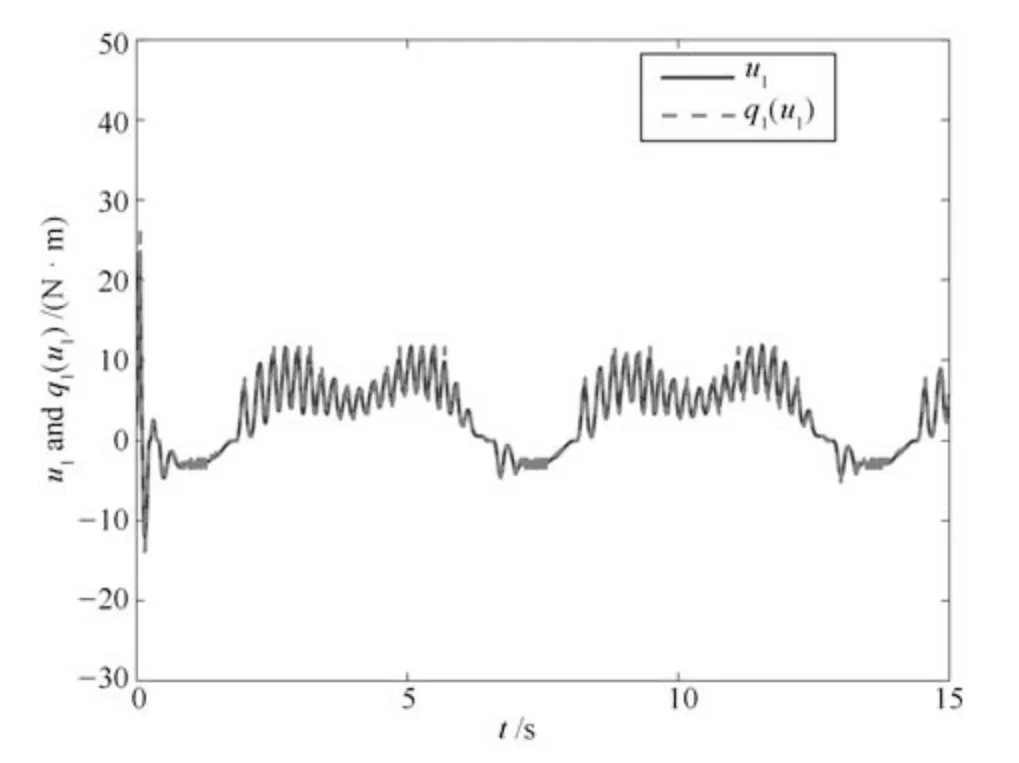
图14 量化参数未知时输入u1和q1(u1)的轨迹Fig.14 Trajectories of input u1 and q1(u1)with unknown quantization parameters

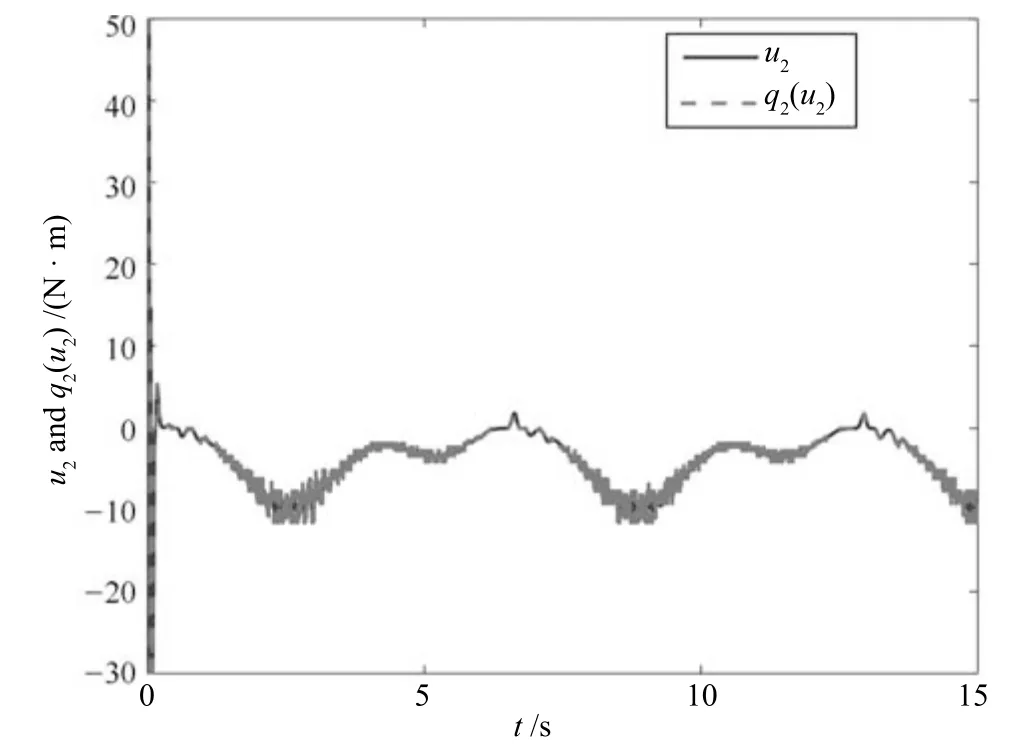
图15 量化参数未知时输入u2和q2(u2)的轨迹Fig.15 Trajectories of input u2 and q2(u2)with unknown quantization parameters

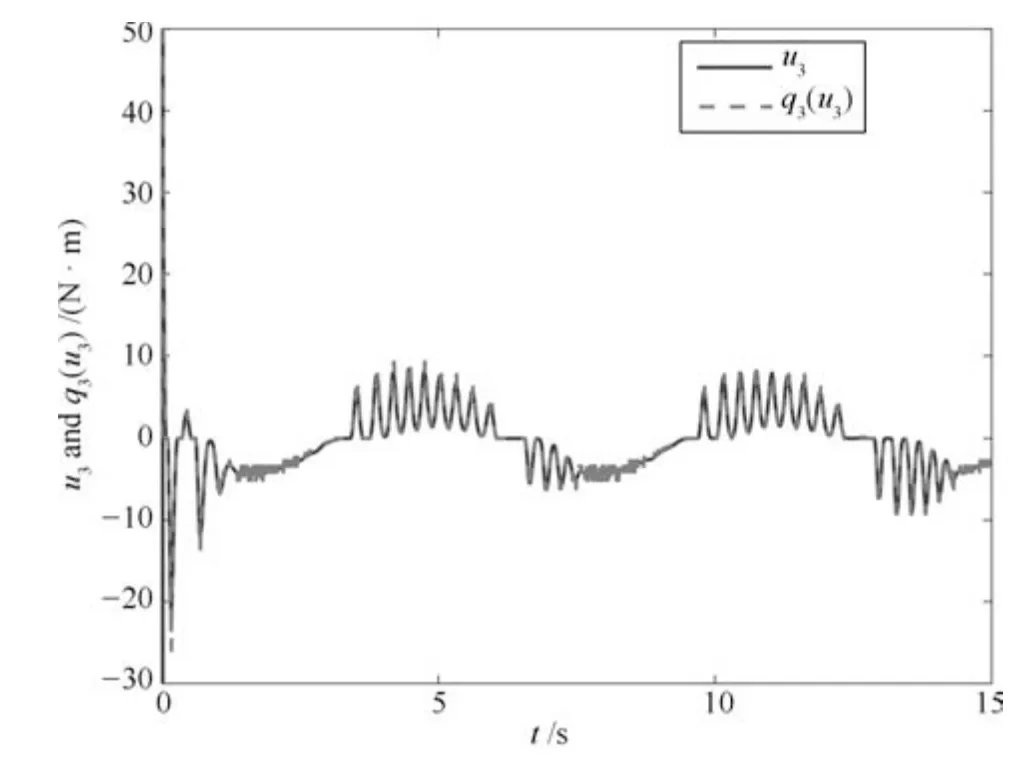
图16 量化参数未知时输入u3和q3(u3)的轨迹Fig.16 Trajectories of input u3 and q3(u3)with unknown quantization parameters

本文考虑一类带有输入量化和输出受限的大型非线性互联系统的输出跟踪控制问题.本文主要贡献是放宽了互联项的假设条件,基于反推法和神经网络逼近特性,分别考虑量化参数已知和未知的情况,设计出一种新的自适应量化跟踪控制策略;同时,在反推法的设计过程中引入障碍李雅普诺夫函数,确保了系统输出信号都不违反约束条件;最终,理论分析和仿真结果验证了输出跟踪误差收敛和闭环系统所有信号一致有界的结论.