一类含分数阶阻尼的三维波导中的传播问题

葛志新, 李春源, 陈咸奖

(1- 安徽工业大学数理学院，马鞍山 243002; 2- 安徽工业大学商学院，马鞍山 243002)

1 引言

分数阶导数的Riemann-Liouville 定义和Caputo 定义[1-3]，都含有自变量的卷积部分的积分，可以表示对自变量的累积效应，因此对沾滞问题、记忆问题和遗传问题有很好的描述.近年来，学术界对分数阶导数的研究已形成热点，学者们已广泛研究了分数阶导数的各种性质，在微分方程领域也掀起了研究的热潮，研究各种类型方程的分数阶导数对解的影响[4-16].所用方法有数值法、迭代法、多重尺度法.多种数学方法的发展，使我们能够更好的研究各种数学模型的性质.例如利用多重尺度法研究二维方程的波动问题[13].在波动问题中，对二维方程研究比较多，对三维波动方程模型研究比较少.我们遇到的实际波动问题往往非常复杂，例如地震勘探、石油勘探的弹性波，这些都是三维问题，或者是多种波动的合成.

本文从摄动的角度，对用分数阶导数表示负阻尼的三维波动方程[13]进行研究.考虑三维波在沾滞的介质中传播问题

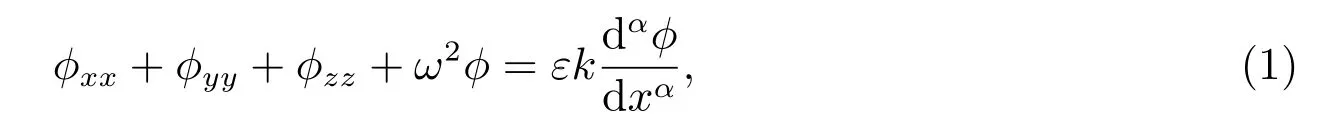
2 渐近解

我们将φx(x,y,1+εsinkωx), φz(x,y,1+εsinkωx)在z=1 处展开，得

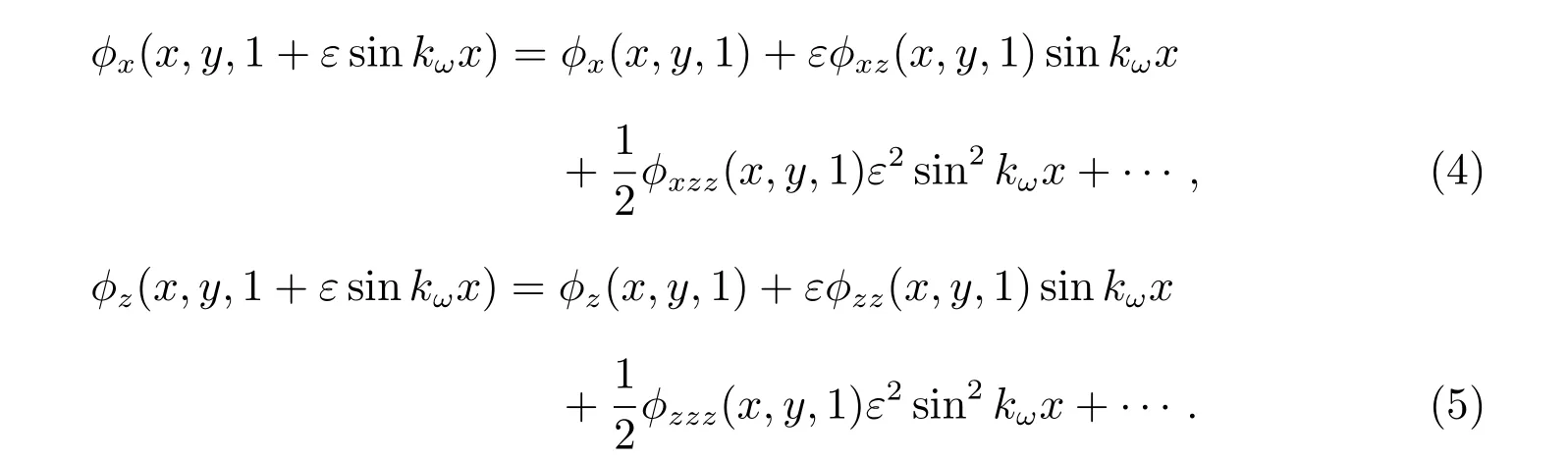
将(4),(5)代入(3)得

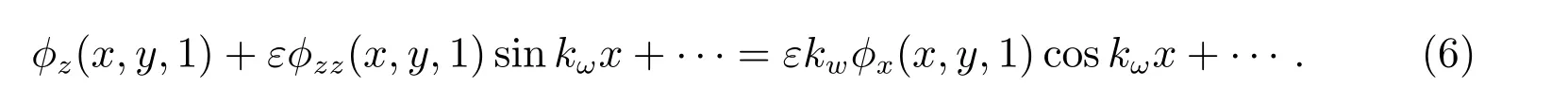
引入多重尺度x0=x, x1=εx，则

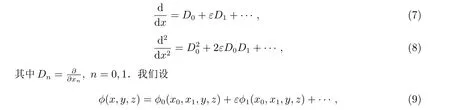
并把(7)—(9)代入到(1),(2),(6)中，比较ε同次幂的系数得

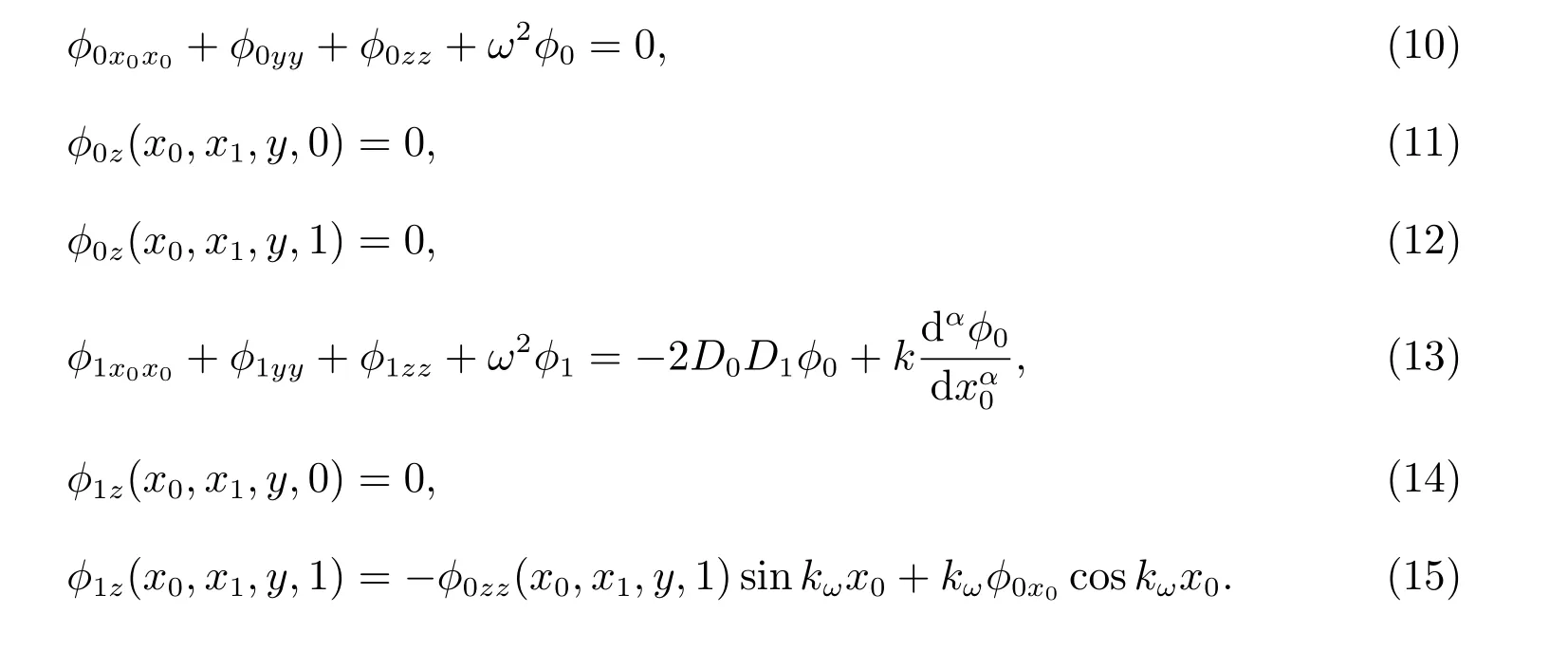
利用分离变量法，设(10)的解为φ0(x0,x1,y,z) =X(x0)Y(y)Z(z)，由方程形式可以解出方程，其解为

所以，(13),(15)转化为

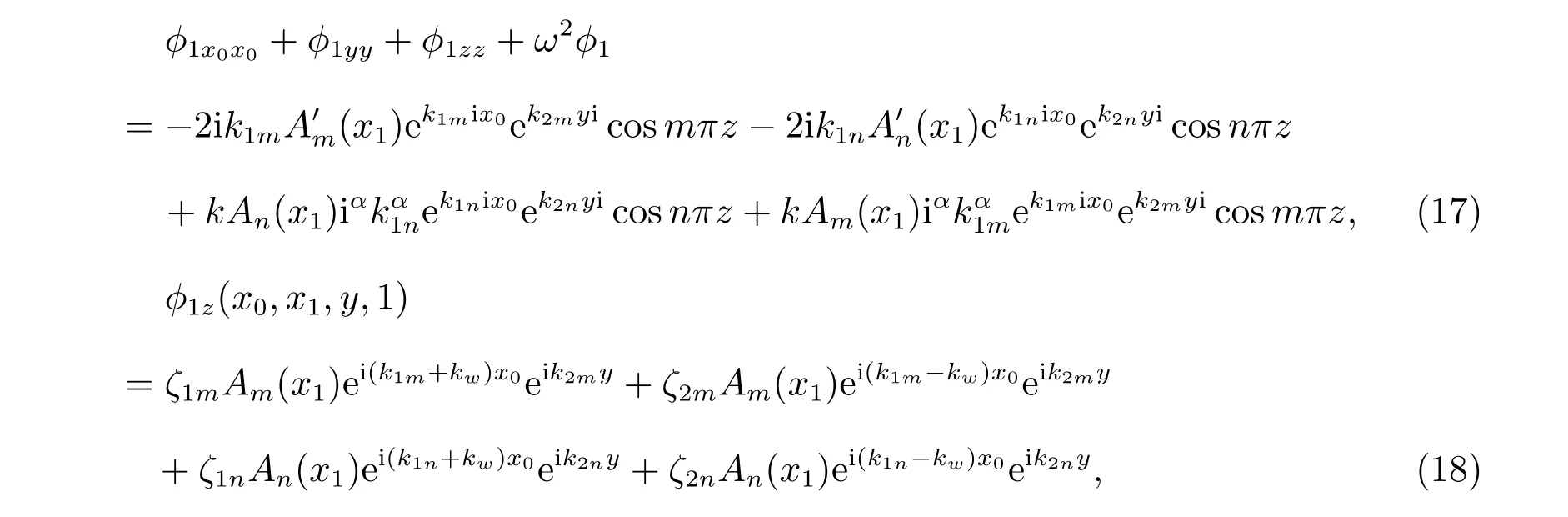
其中

即

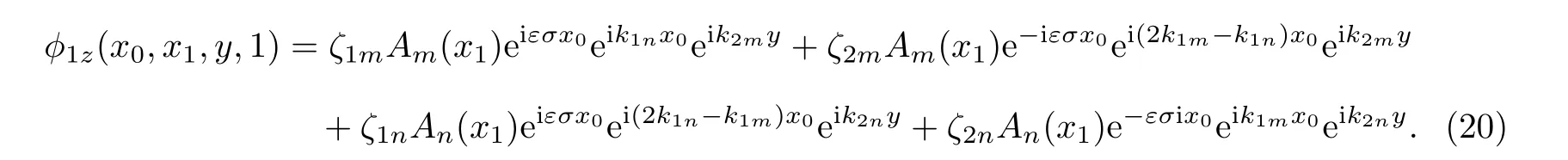
我们寻找下式的解

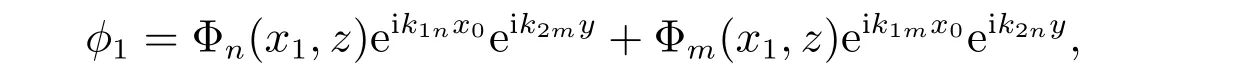
即

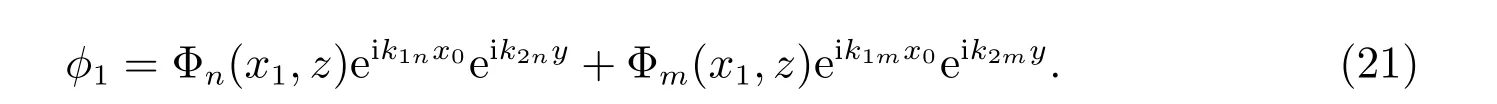
我们把(21)代入(14),(17),(18)，得

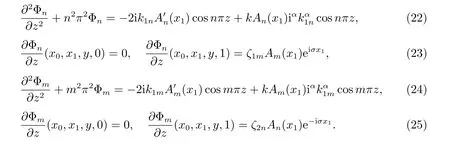
因为方程(22)是自伴的，取伴随问题的解[13]u= cosnπz，方程(22)两边都乘以u=cosnπz，并在[0,1]上积分.利用分部积分法，我们可以得到可解性条件

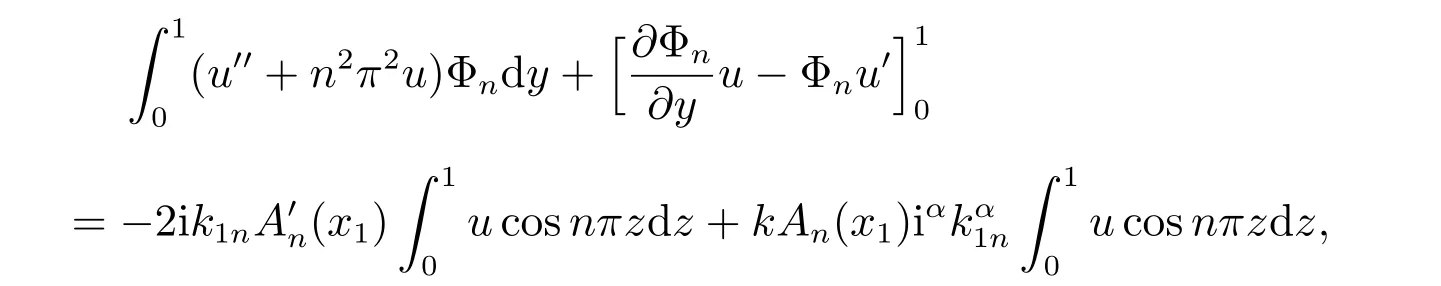
即

利用(23)得

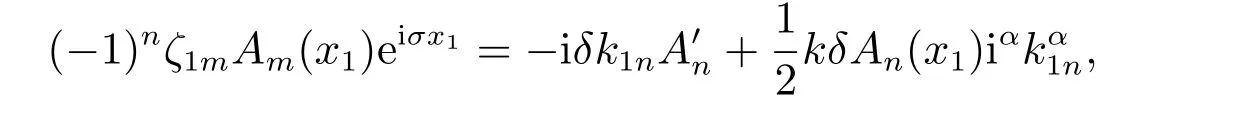
即

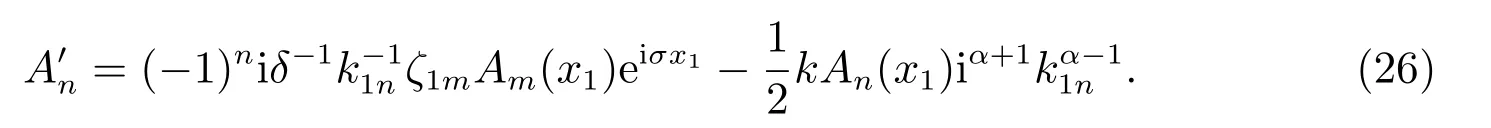
同理由(24),(25)，当m/=0 时，有

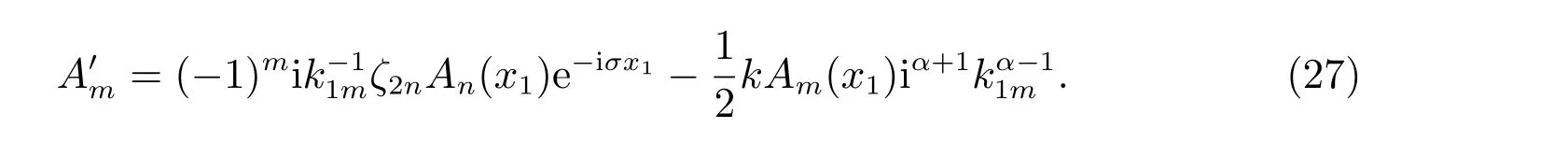
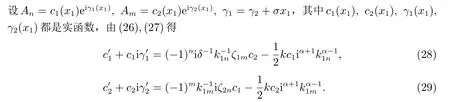
把(28)虚实部分开，得

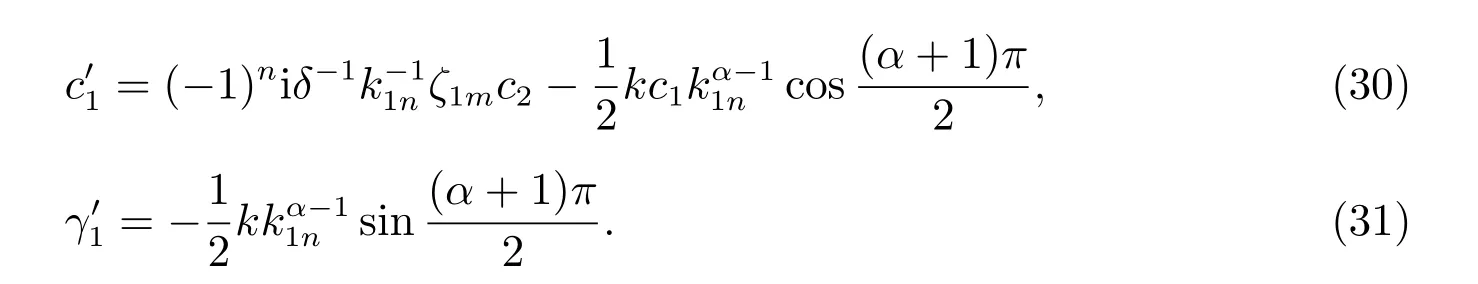
把(29)虚实部分开，得

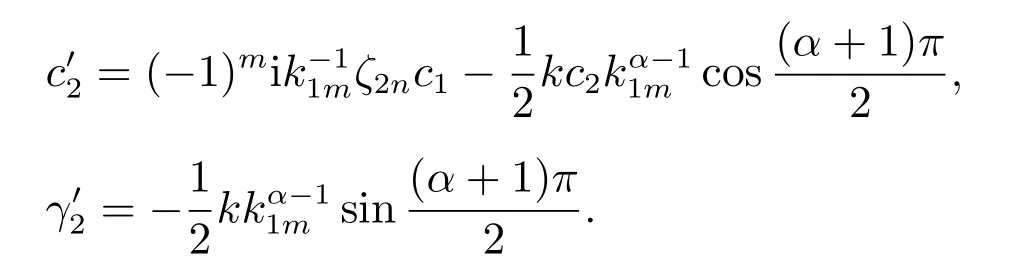
由(30)—(33)，Am, An立刻被解出，取Am, An实部，代入(16)的Am, An中，从而得到(16)的表达式.

3 一致有效性

设

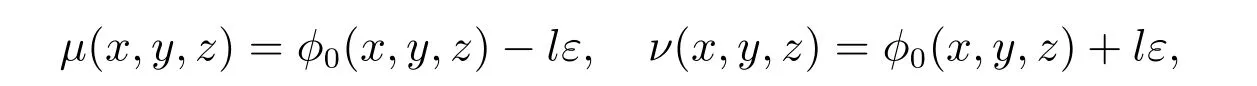
这里l是正常数.我们可以发现μ(x,y,z)≤ν(x,y,z)，且由式(2),(3)得μz(x,y,0)≤0≤νz(x,y,0),

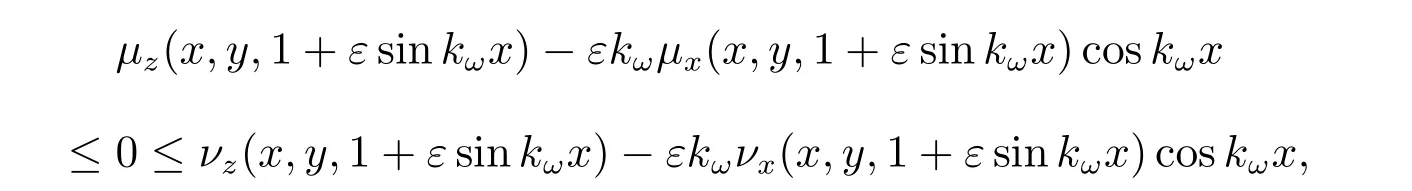
并且，由式(10),(13)知

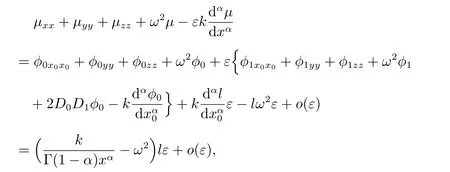
所以，当x ∈(0,1)时，lgx ＜0，因为0＜α ＜1，所以xα=10αlgx ∈(0,1).因此

从而

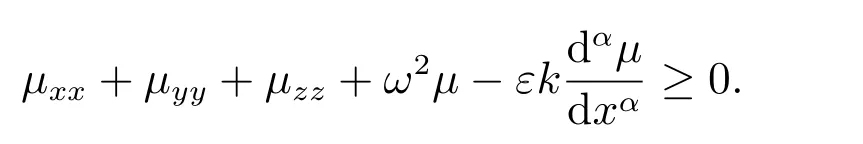
同理

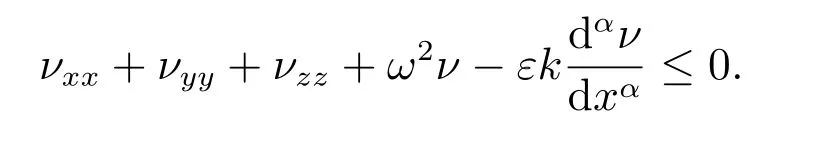
由φ0(x,y,z)知

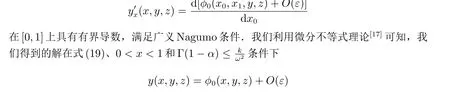
是一致有效的.

4 三维波的解的分析

三维波动边值问题说明，只要边界发生正弦型波动，垂直这个边界上的外力有规律地变化，则该波有一个近似解，该解的振幅的模和相位的瞬时变化率，由边界取值、最初选择的模态值和α, k的取值确定.可以发现没有阻尼二维波[13]与三维波的解的振幅有很大差异.二维波仅仅是振幅相位在周期变化，振幅模却恒定，近似解是周期解.三维波是振幅模和相位两者都在变化.变化规律如图1 和图2 所示.图1 为c1-x和c2-x曲线，其中ω= 3π, m= 2, n= 1, α= 0.5, k2m=k2n=π, σ= 1, ε= 0.01, c1(0) =1, c2(0)=1.图2 为γ1-x和γ2-x曲线，其中ω=3π, m=2, n=1, α=0.5, k2m=k2n=π, σ= 1, ε= 0.01, γ1(0) = 0, γ2(0) = 0.图中x皆是上文中的x1.三维波的振幅不是周期解.

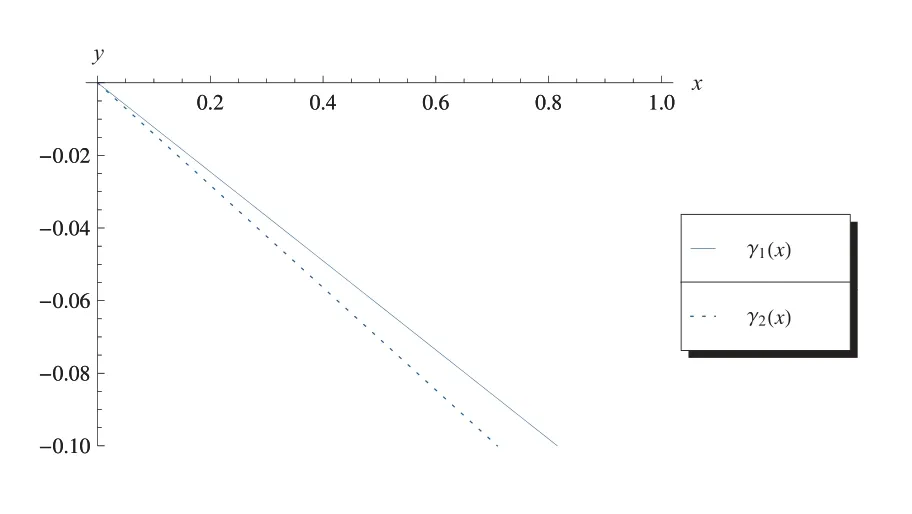
图2 γ1-x 和γ2-x 曲线

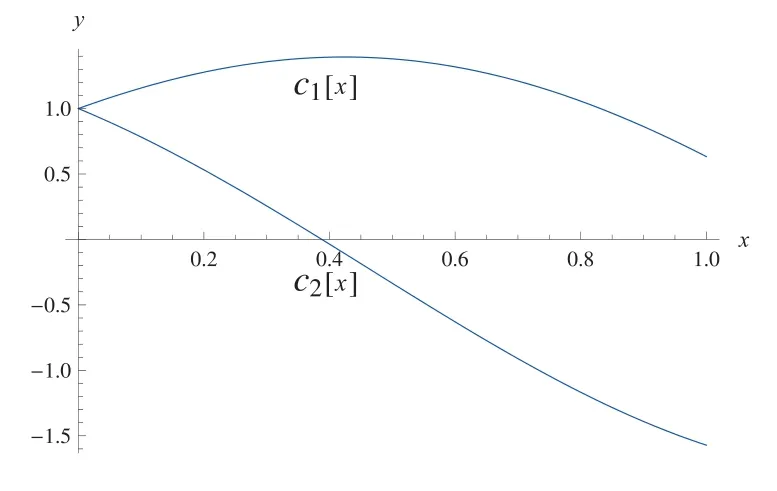
图1 c1-x 和c2-x 曲线

振幅的模与相位同选择的模态有关，如图3 至图6 所示.图3 为c1-x曲线，其中ω=5π, α= 0.5, k2m=k2n=π, σ= 1, ε= 0.01, c1(0) = 1, c2(0) = 1.图4 为c2-x曲线，其中ω= 5π, α= 0.5, k2m=k2n=π, σ= 1, ε= 0.01, c1(0) = 1, c2(0) = 1.图5 为γ1-x曲线，其中ω= 5π, α= 0.5, k2m=k2n=π, σ= 1, ε= 0.01, γ1(0) =0, γ2(0) = 0.图6 为γ2-x曲线，其中ω= 5π, α= 0.5, k2m=k2n=π, σ= 1, ε=0.01, γ1(0)=0, γ2(0)=0.

图6 γ2-x 曲线

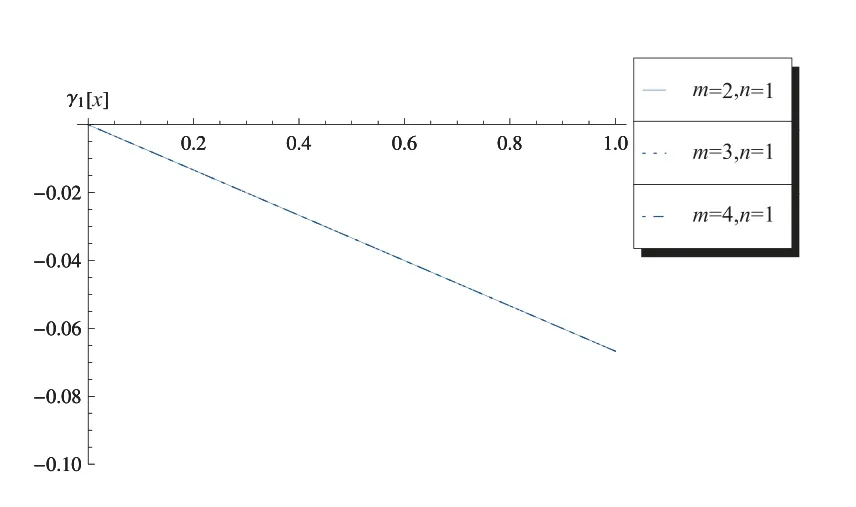
图5 γ1-x 曲线

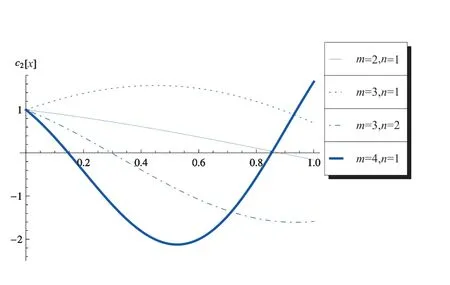
图4 c2-x 曲线

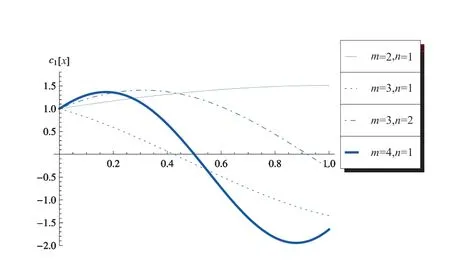
图3 c1-x 曲线

由图7 至图10 也可发现，分数阶导数α不同，振幅的模发生改变.图7 为c1-x曲线，其中ω= 3π, m= 2, n= 1, k2m=k2n=π, σ= 1, ε= 0.001, c1(0) =1, c2(0) = 1.图8 为c2-x曲线，其中ω= 3π, m= 2, n= 1, k2m=k2n=π, σ=1, ε= 0.001, c1(0) = 1, c2(0) = 1.图9 为γ1-x曲线，其中ω= 3π, m= 2, n=1, k2m=k2n=π, σ= 1, ε= 0.001, γ1(0) = 0, γ2(0) = 0.图10 为γ2-x曲线，其中ω=3π, m=2, n=1, k2m=k2n=π, σ=1, ε=0.001, γ1(0)=0, γ2(0)=0.

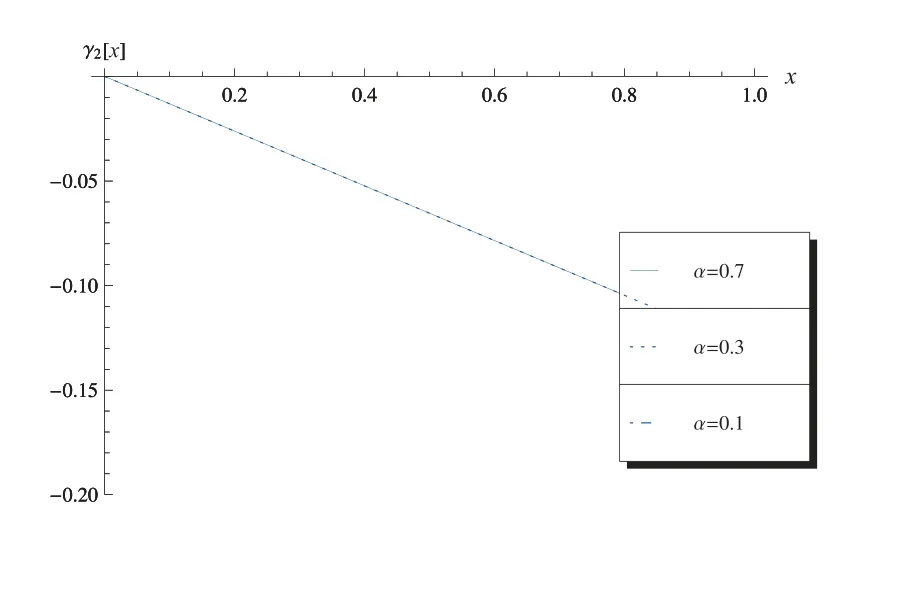
图10 γ2-x 曲线

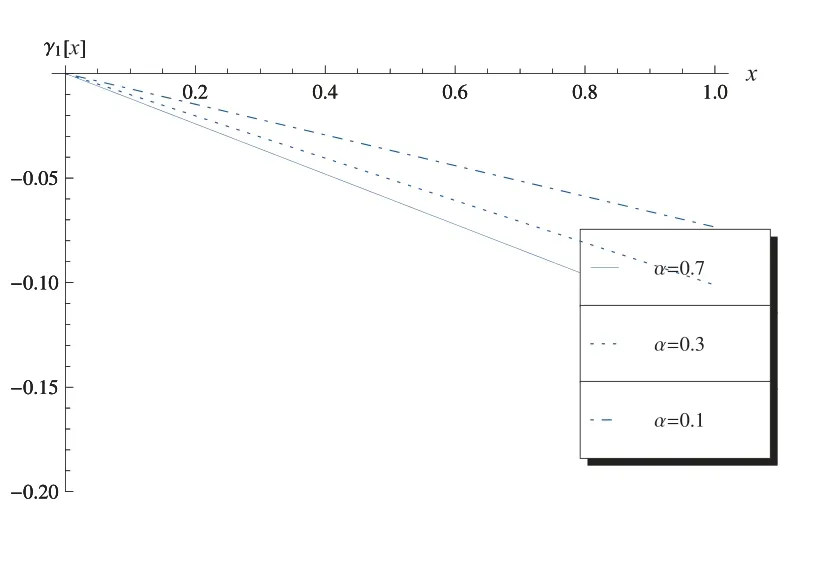
图9 γ1-x 曲线

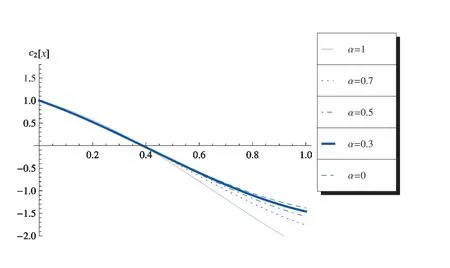
图8 c2-x 曲线

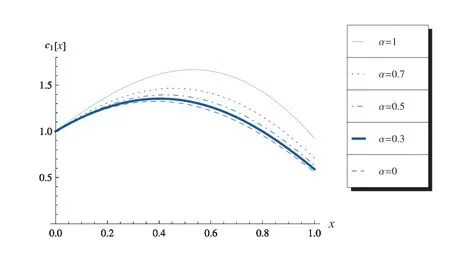
图7 c1-x 曲线

进而，由图11 和图12 可以看出，在其他参数不变的情况下，σ的改变对零阶近似解的影响不大，ε的改变对零阶近似解的影响也不大.图11 为c1-x曲线，其中ω=5π, α= 0.5, m= 2, n= 1, k2m=k2n=π, ε= 0.01, c1(0) = 1, c2(0) = 1.图12 为c1-x曲线，其中ω= 5π, α= 0.5, m= 2, n= 1, k2m=k2n=π, σ=1, c1(0)=1, c2(0)=1.

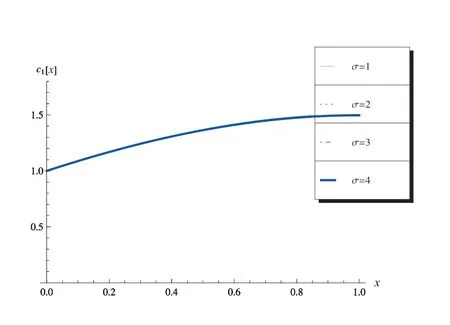
图11 c1-x 曲线

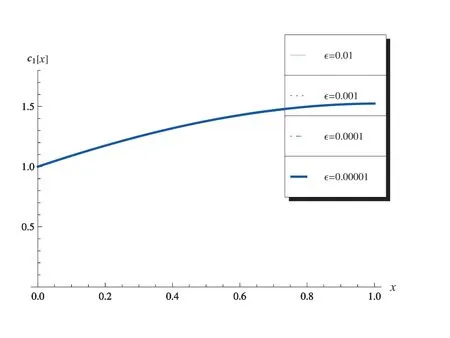
图12 c1-x 曲线