天然地震波强度及频率非平稳特征的影响因素

2021-06-19杨开来殷翔晁增辉白永祯韩旭

高原地震 2021年1期

关键词：级数导数幅值

杨开来，殷翔，晁增辉，白永祯，韩旭

(青海省地震局，青海西宁 810001)

0 引言

前人研究表明，天然地震波的强度非平稳特征是指其加速度时程曲线的高低起伏规律随着持续时间的改变而改变，而频率非平稳特征是指其频率组成在前期阶段的高频成分含量较多，在后期阶段的高频成分逐渐减少且低频成分逐渐增加[1]。

目前，我国建筑抗震设计规范中建议采用由Scanlan和Sachs[2]提出的三角级数方法合成人工地震波。但是，利用上述方法合成的人工地震波不仅不具备频率非平稳特征，而且其强度非平稳特征也会受到人为假定包络函数的不利影响。

为了合成兼具强度及频率非平稳特征的人工地震波，国内外学者针对天然地震波特性展开研究，具体包括相位差谱和时变功率谱。首先，日本大崎顺彦[3]提出了相位差谱的概念，认为天然地震波相位谱的频率分布特征服从[-π，π]范围内的均匀分布，而相位差谱的频率分布特征却近似服从正态分布。程纬[4]、朱昱[5-6]谭俊林[7]艾晓秋[8]、尹广斌[9]等学者利用对数正态分布对经过平移调整的相位差谱频率分布特征进行拟合，不仅根据均值λ和标准差ξ生成代表人工相位差谱，而且还合成了兼具强度及频率非平稳特征的人工地震波。除此之外，还有其他学者利用时变功率谱合成兼具强度及频率非平稳特征的人工地震波。例如，Kameda[10]运用多重滤波技术分析天然地震波的时变功率谱模型，并将其与人工相位谱代入三角级数公式中，合成一条兼具强度及频率非平稳特征的人工地震波。我国学者符圣聪[11]梁建文[12-13]、钟菊芳[14]等利用不同方法得到不同形式的时变功率谱模型，并通过三角级数计算公式，合成能够兼具强度及频率非平稳特征的人工地震波。

研究发现，相位差谱或时频功率谱均属于天然地震波的单一频域指标，利用任何一个参数均可以保证人工地震波具备强度及频率非平稳特征。但是，由于人工地震波在合成过程中受到相位谱和幅值谱的双重影响，因此利用上述方法合成的人工地震波，其强度及频率非平稳特征又与天然地震波之间存在明显差距。例如，利用相位差谱合成的人工地震波，其强度非平稳特征明显弱于天然地震波，而利用时变功率谱合成的人工地震波，其频率组成在不同时间段的数量分布又缺乏天然地震波自身的差异性。

本文以三角级数转换公式作为理论基础，推导出控制频率组成最大值出现时间的相位导数，并利用相位导数分析天然地震波的强度及频率非平稳特征的全部影响因素。选取某条天然地震波为研究对象，利用傅里叶变换分析天然地震波的影响因素变化特征，验证各因素的影响效果。选取不同条件下的大量天然地震波作为数据库，总结天然地震波的强度及频率非平稳特征的影响因素的变化规律。本文不仅分析了天然地震波的强度及频率非平稳特征，而且还为人工地震波的合成过程提供优化依据。

1 相位导数的概念与计算

利用傅里叶变换对天然地震波进行频谱分析，将其加速度时程表示为三角级数叠加形式，如公式(1)所示：

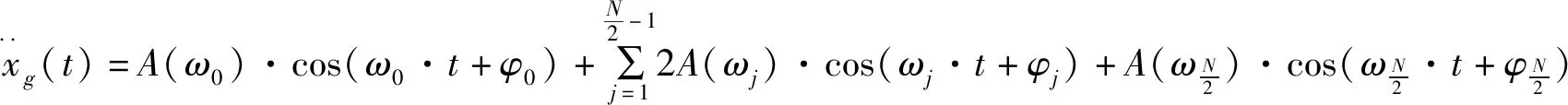
(1)

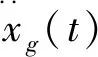
假设天然地震波相邻频率点对应的幅值大小相近，那么利用三角级数和差化积进行变换分析，如公式(2)所示：

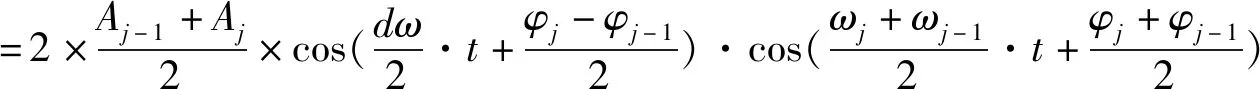
(2)

将能够代表天然地震波加速度时程的三角级数叠加公式简化为：

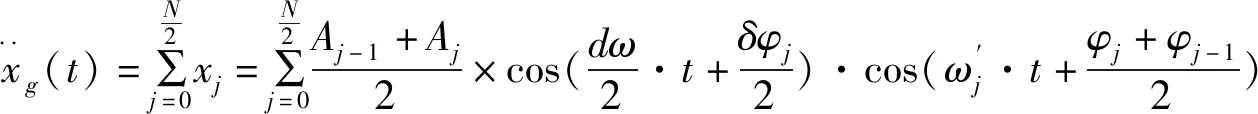
(3)

(4)

由此可知，天然地震波中三角级数xj的峰值到达时间tj是由相位导数[15-16]决定的，计算公式为:

(5)

2 频率非平稳特征对地震动影响分析

如公式(6)所示，天然地震波的加速度时程可以通过三角级数叠加公式表达：

(6)

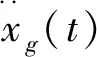
相位谱φj可由初始相位角与相位差谱计算得到，如公式所示：

(7)

式中，φ0为初始相位角，通常假定为0；δφj为人工相位差谱，可以通过人工相位导数计算得到，如公式所示：

(8)

将人工相位谱代入三角级数公式中，得到：

(9)

式中，δω为天然地震波的频率间隔；ti为第i个相位导数；ωj为第j个圆频率分量，如公式所示：

(10)

人工地震波三角级数公式为:

(11)

进一步，可以推导出：

(12)

如果将天然地震波的持续时间T划分为若干段，并针对其中某个时间段td展开研究，那么其三角级数公式为:

(13)

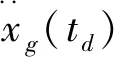
为了能够直观分析强度及频率非平稳特征的影响效果，首先需要根据时间与频率之间的转换关系将幅值谱与相位导数建立联系，具体公式为:

(14)

(15)

3 强度及频率非平稳特征的影响因素

3.1 相位导数频率分布特征的变化规律

图1 ElCentro地震波相位导数图2 Norbridge地震波相位导数

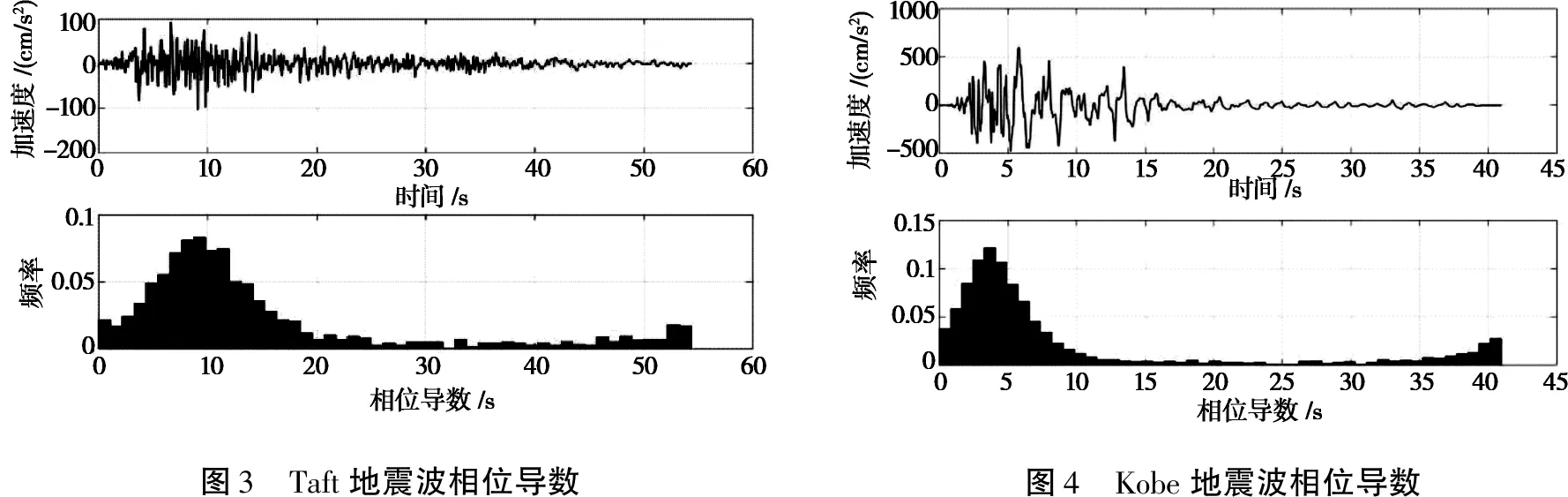
图3 Taft地震波相位导数图4 Kobe地震波相位导数

如图1～4所示，本文选取El Centro、Norbridge、Taft和Kobe等4条天然地震波，分别做出加速度时程曲线与相位导数频率分布直方图，对比分析二者的变化规律可以得到下列结论：

(1)天然地震波的持续时间与相位导数的变化范围完全相同，这是由于相位差谱的频率分布范围为[0，2π]，而天然地震波自身的频率差值为dω，二者相除得到的相位导数频率分布范围等于[0，T]，其中T代表着天然地震波包含的三角级数峰值加速度的最大出现时间。

(2)天然地震波加速度时程曲线的高低起伏变化规律与相位导数的频率分布特征大致相同，而且天然地震波的相位导数均值μ及标准差σ分别体现了天然地震波加速度峰值出现时间及加速度峰值附近的增加衰减规律。

3.2 相位导数对应幅值谱的变化规律

(16)

式中，a(t)为天然地震波的加速度时程曲线；:T为天然地震波的持续时间；I(t)为从0到1的能量归一化函数。

为了能够详细分析天然地震波的频率非平稳特征变化规律，本文将天然地震波的持续时间T按照能量累计规律进行划分，并分别计算当归一化系数I(t)等于2.5%、5%、10%、15%、25%、50%、75%、85%、90%、95%、97.5%时的时间节点。

以图5中的天然地震波为例，将持续时间T划分为12个阶段，分别为(0～3.96)s、(3.96～4.95)s、(4.95～6.58)s、(6.59～6.9)s、(6.9～7.56)s、(7.56～8.69)s、(8.69～9.83)s、(9.83～11.67)s、(11.67～12.23)s、(12.23～14.71)s、(14.71～17.66) s和(17.66～38.47)s。

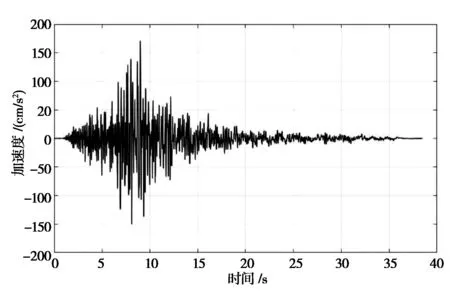
图5 天然地震波加速度时程曲线

图6 不同时间段幅值谱变化规律

如图6所示，天然地震波在任意时间段范围内的相位导数对应幅值均表现出左右对称特征，而且不同持续时间范围内的幅值分布数量及最大幅值变化规律均表现出非平稳特征，包括以下两方面结论：

(1)天然地震波在不同时间范围内的幅值分布数量表现出了明显的非平稳特征，其中，在9 s以前的幅值分布数量随着持续时间的增加而逐渐增加，在9 s左右达到幅值分布数量的最高值，而在9 s以后的幅值分布数量随着持续时间的增加而逐渐减少。

(2)天然地震波在不同时间段范围内的最大幅值同样表现出了非平稳特征，其高低起伏变化规律与频率分布特征大致相同，即在(0～10)s范围内的最大幅值随着时间的增加而逐渐增加，在(10～12) s范围内的幅值达到峰值以外，在12 s之后的最大幅值逐渐降低。

3.3 相位导数与幅值的对应关系变化规律

本文参考场地类别、烈度及震中距等多方面因素，选取Ⅰ-Ⅳ类场地条件下的57条天然地震波作为研究对象。为了汇总分析不同天然地震波的幅值谱变化规律，本文将幅值谱按照最大幅值的百分比划分为五部分，分别为(0.1～1)%、(1～10)%、(10～25)%、(25～50)%和(50～100)%，具体代表了小幅值区域、较小幅值区域、中等幅值区域、较大幅值区域及大幅值区域。

利用下列公式分别计算在不同时间段范围内的幅值分布比例系数pij，具体公式为：

(17)

式中，i为某个相位导数分布范围；j为某个范围内的幅值分布数量；n为天然地震波的全部幅值数量。

如表1所示，本文分别计算每条天然地震波在不同持续时间范围内的幅值分布数量及幅值大小的比例系数。

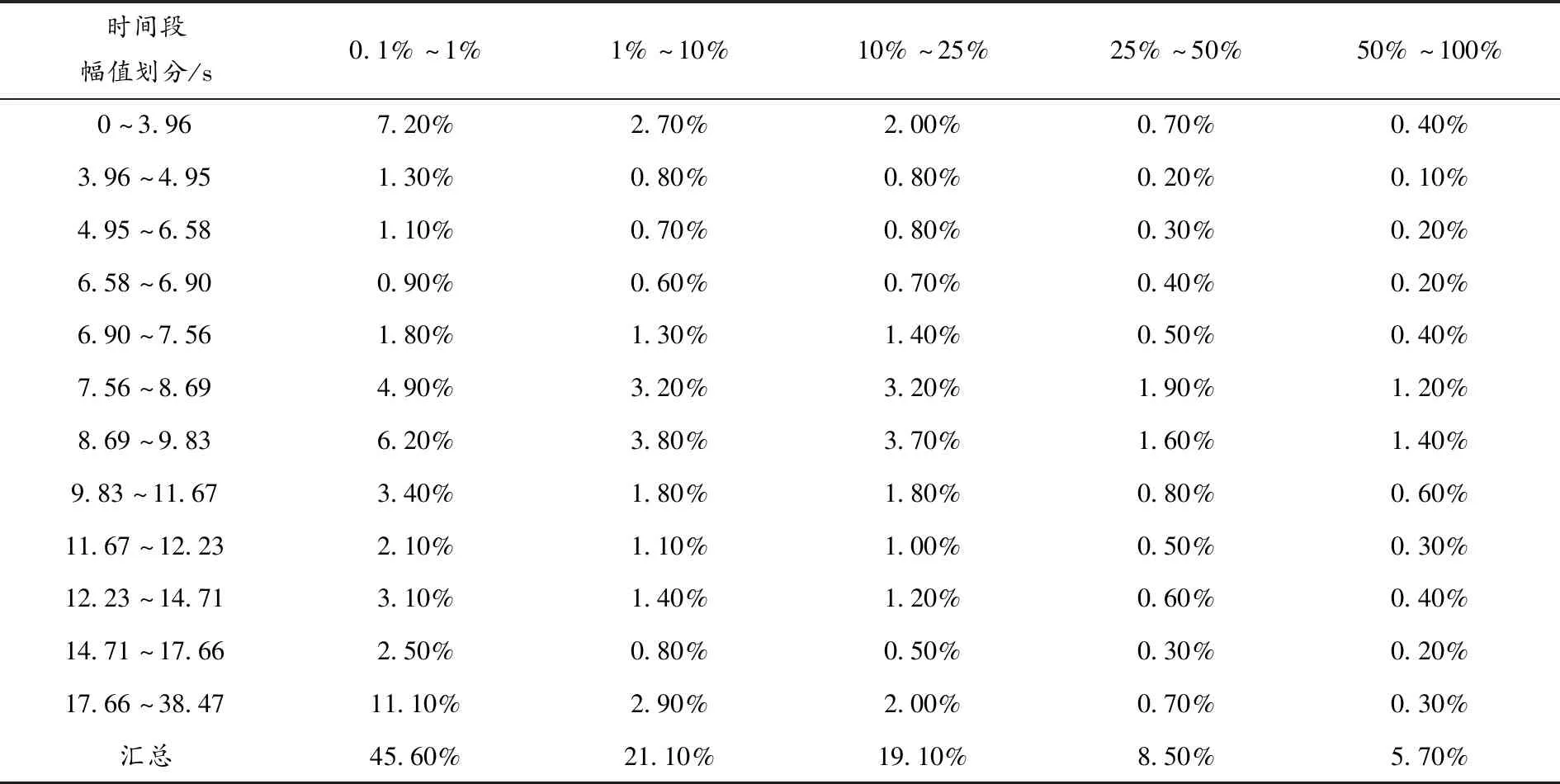
表1 天然地震波幅值分布比例系数

如表1所示，天然地震波在不同时间范围内的幅值分布变化规律包括以下几方面结论：

(1)天然地震波在整个持续时间范围内的幅值分布数量表现出了明显的非均匀特性，其不同大小范围内的幅值分布比例系数依次等于45.6%、21.1%、19.1%、8.5%和5.7%，即幅值分布数量随着幅值增大而逐渐降低。

(2)天然地震波低于1%的小幅值分布数量具有明显的时频非平稳特征，其中在(17.66 ～38.47) s范围内的小幅值分布比例系数最高，在(0～3.96)s范围内的分布比例系数紧随其后，而其余范围内的分布比例系数则相对较小；天然地震波高于50%的大幅值分布数量同样表现出了时频非平稳特征，其中在(7.56～9.83) s范围内的大幅值分布数量比例系数最大，而其余时间范围内的大幅值分布比例系数大致相等；

(3)天然地震波在不同时间段范围内的幅值分布比例系数随着幅值增大而逐渐均等，其中低于1%的小幅值分布比例系数差异性最为显著，高于50%的大幅值分布比例系数差异性次之，而介于(1～50)%范围内的幅值分布比例系数差异性并不突出。