基于模糊误差判断算法的航空发动机PID 控制

陈 勇,蔡开龙

(南昌航空大学通航学院,江西 南昌 330063)

0 引言

航空发动机被归类于强非线性被控对象,其气动热力过程十分复杂,而且工作环境恶劣[1]。在飞行包线内,由于飞行环境和飞行状态的不断改变,需要控制航空发动机在任何变化的条件下都能正常工作,并充分发挥发动机的性能效益[2]。普通比例-积分-微分(proportial integral differential,PID)算法与其他智能算法相比,具有结构简单、容易实现等特点,在生产实践中被大量采用[3]。但是普通PID 应用于航空发动机控制时,对非线性信号的追踪不是很理想,非常有局限性,不能很好地满足航空发动机的控制要求。随着控制方法的不断创新,多种智能控制方法被提出,如基于遗传算法的PID 控制[4]、基于神经网络算法的PID 控制[5]、基于模糊算法的PID 控制[6]等。

本文提出模糊误差判断PID 控制:由模糊规则表、误差判断规则以及PID 控制器构成模糊误差判断PID控制器。根据仿真结果,模糊误差判断PID 算法能够很好地适应航空发动机工作过程的多变性、复杂性,对航空发动机的控制效果良好。

1 航空发动机控制系统

1.1 航空发动机转速控制系统

本文设计的基于模糊误差判断算法的航空发动机PID 控制系统如图1 所示。

图1 基于模糊误差判断算法的航空发动机PID 控制系统图Fig.1 Aero-engine PID control system based on fuzzy error judgment algorithm

图1 中:NfR为转速参考指令;Nf为发动机转速;er为转速参考指令与发动机转速的偏差;U为模糊误差判断PID 控制器输出;Wf为主燃烧室供油量。

该控制系统由转速参考指令NfR与发动机转速Nf得到偏差er;然后将偏差er输入模糊误差判断PID 控制器,由模糊误差判断PID 控制器根据输入量er计算出控制量U,并且发送给执行机构;执行机构将根据控制量U计算出航空发动机正常运转所需燃油量。

1.2 基于模糊误差判断PID 控制器

1.2.1 普通PID 控制器

普通的PID 控制就是通过偏差与常数的乘积、对时间的积分和对时间的微分组合计算出控制量,对被控对象进行控制[7]。PID 控制规律为:

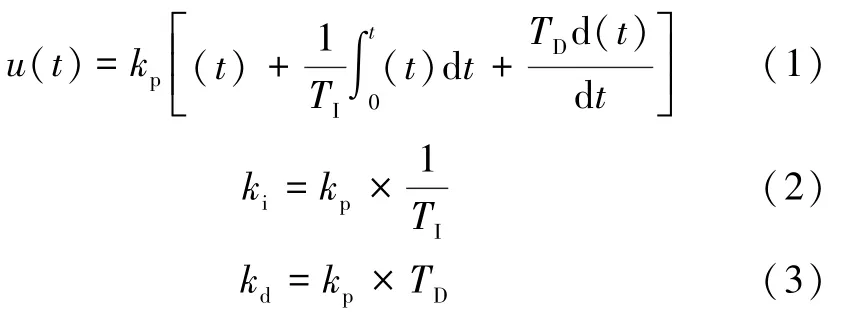
式中:kp为比例系数;TI为积分时间常数;TD为微分时间常数。

①比例环节(P):信号偏差与常数的乘积为比例环节P。当系统有偏差存在时,比例环节P就能将偏差放大,然后作为控制量输出,以减小偏差。

②积分环节(I):信号偏差对时间的积分为积分环节I。积分环节I对信号偏差进行积分。由于偏差的不断积累,控制系统的静差将被减小。

③微分环节(D):信号偏差对时间的微分为微分环节D。微分环节对系统震荡有抑制作用,能够有效减少系统的调节时间,使控制系统更快速地达到稳定。

1.2.2 模糊控制

(1)模糊控制介绍。

美国控制理论学家L.A.Zadeh 曾发表过论文“Fuzzy Set”,提出了有关模糊集合的思想。自20 世纪70 年代以后,模糊控制算法开始被应用于生产实践,使得控制理论的发展又向前迈出了一大步[8]。模糊控制是运用模糊数学的基本思想,使用语言型控制规则,使算法的控制原理易于理解,设计简单,容易实现[9]。模糊控制系统主要由四个部分构成,分别为模糊化模块、知识库模块、模糊推理模块和清晰化模块。模糊控制器原理如图2 所示。

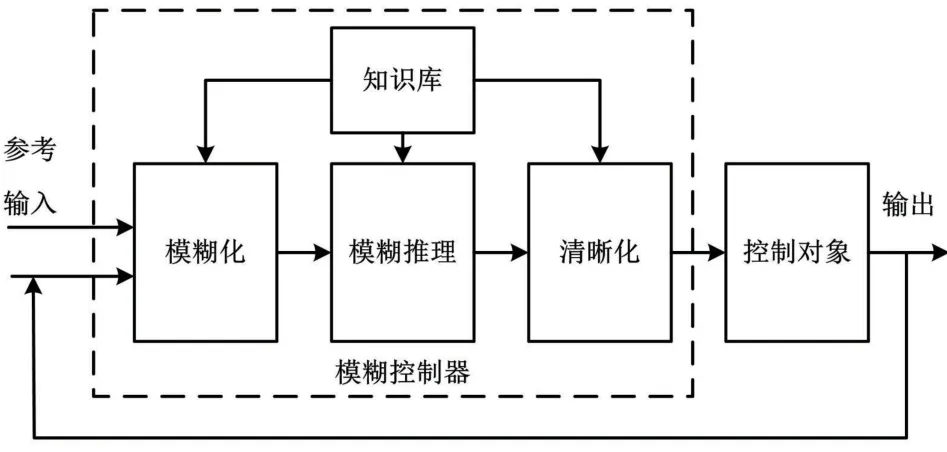
图2 模糊控制器原理图Fig.2 Schematic diagram of fuzzy controller

①模糊化。模糊化是将输入根据相对应规则转换为模糊化量。

②知识库。知识库由数据库和模糊控制规则库组成。数据库中有模糊数据处理相关的各种参数。模糊规则库则由一系列模糊条件句构成。

③模糊推理。模糊推理是控制器的核心部分。它是根据人脑作出判断的思维能力设计的,由相对应的模糊规则进行推理。

④清晰化。清晰化是将模糊推理得到的值转化为明确的值。

(2)模糊规则表控制原理。

①分别采用三个隶属函数对误差er及误差变化Δer进行模糊化:

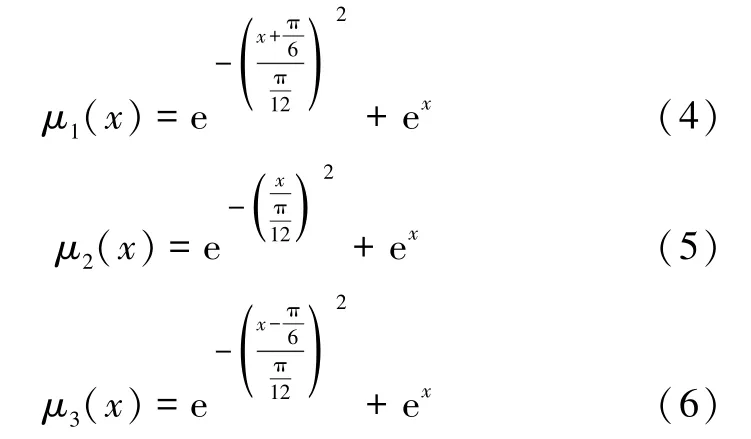
根据实际被控对象,设计的模糊控制规则表如表1 所示。

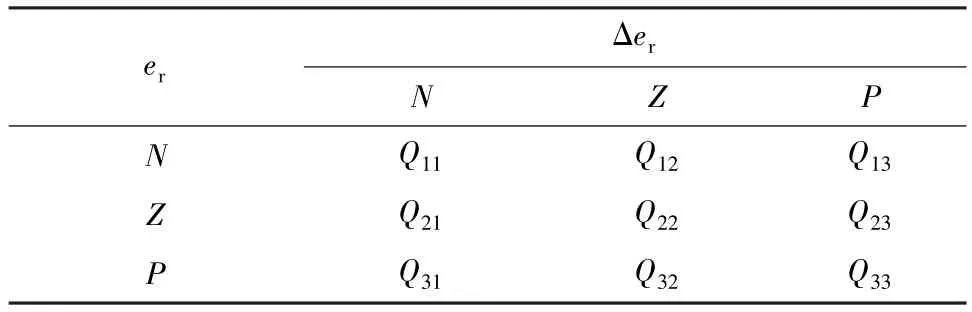
表1 模糊控制规则表Tab.1 Fuzzy control rules table

(3)使用误差和误差变化这两个数据,设计模糊控制规则如下:

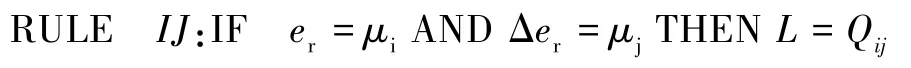
(4)采用重心方法进行反模糊化,得:

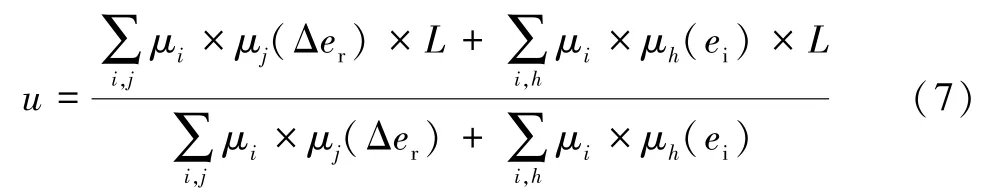
式中:i=1,2,3;j=1,2,3;h=1,2,3;ei为误差er的积分。

1.2.3 误差判断规则

①该判断规则将根据偏差信号er的大小,判断出修改模糊规则表以及模糊推理迭代次数λ。

②根据误差er(t)、er(t-1)的正负,修改模糊规则表,er(t)为t时刻转速参考指令NfR与发动机转速Nf的偏差。当er(t)≥0、er(t-1)≥0 或er(t)≥0、er(t-1)＜0 时,修改规则如下:

当er(t)＜0、er(t -1)＜0 或er(t)＜0、er(t-1) ≥0 时,修改规则如下:

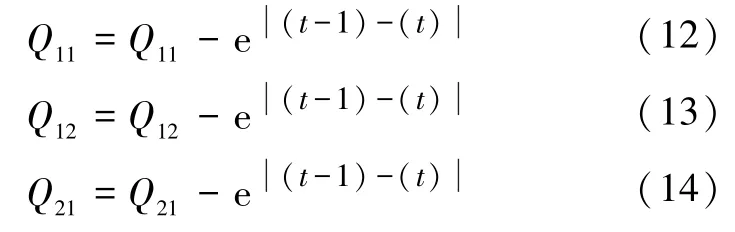
1.3 航空发动机数学模型

本文以某型号民用航空涡扇发动机为例,建立数学模型,然后使用MATLAB 进行仿真。得到执行机构的一般形式传递函数为:

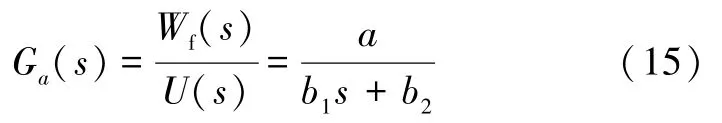
发动机一般形式数学模型为:

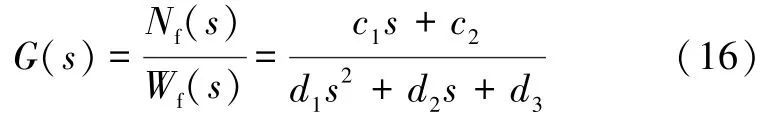
式中:a、b1、b2、c1、c2、d1、d2以及d3都为常数,具体视飞行条件而定。

2 仿真结果

2.1 普通PID 仿真

使用普通PID 控制,用试凑法对PID 进行整定,取kp=1.2、ki=2、kd=0.1。使用MATLAB 对涡扇发动机处于地面状态H=0,Ma=0 和高空状态H=11 km、Ma=0.8 进行仿真;参考文献[10]建立涡扇发动机的数学模型,得到执行机构的传递函数如下 。

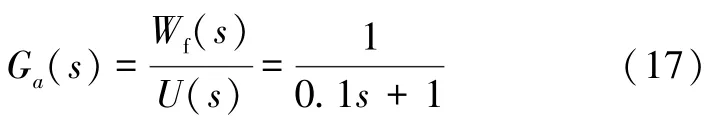
在地面状态,发动机模型为:

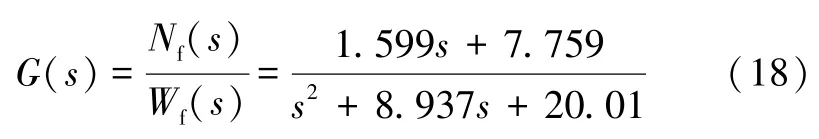
仿真时间为10 s,发动机转速阶跃响应曲线(地面状态,PID 控制)如图3 所示。

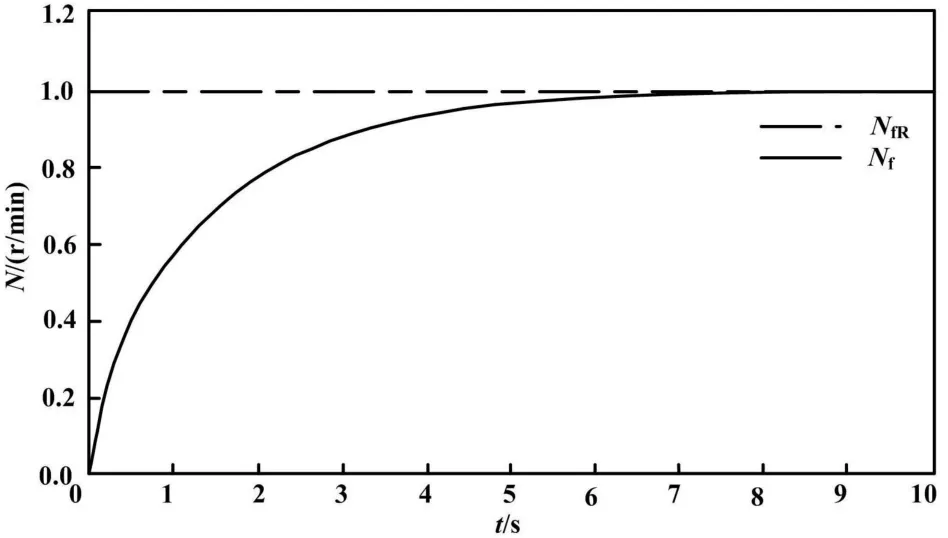
图3 转速阶跃响应曲线(地面状态,PID 控制)Fig.3 Speed step response curves (ground condition,PID control)

在高空状态,发动机模型为:

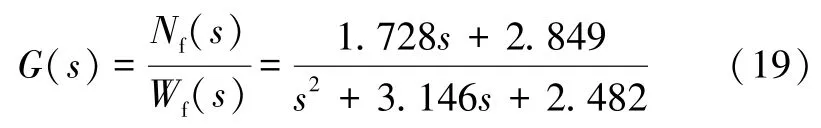
仿真时间为10 s,发动机转速阶跃响应曲线(高空状态,PID 控制)如图4 所示。

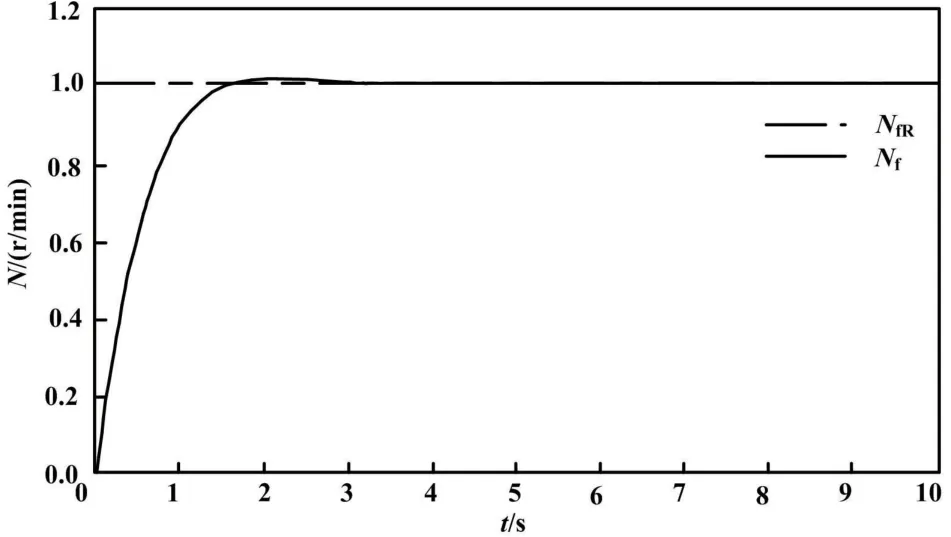
图4 转速阶跃响应曲线(高空状态,PID 控制)Fig.4 Speed step response curves (high altitude condition,PID control)

当处于地面状态进行仿真时,采用阶跃激励,涡扇发动机转速达到平稳状态需要用时9 s;在高空状态仿真时,涡扇发动机转速达到平稳状态需要用时4 s,且有较小超调量。

2.2 基于模糊误差判断算法的PID 仿真

采用模糊误差判断PID 控制方法,使用MATLAB对某型涡扇发动机处于地面状态H=0、Ma=0 和高空状态H=11 km、Ma=0.8 时进行仿真。航空发动机模糊控制规则表如表2 所示。

表2 航空发动机模糊控制规则表Tab.2 Aeroengine fuzzy control rules Table

根据被控对象取g(error)为:

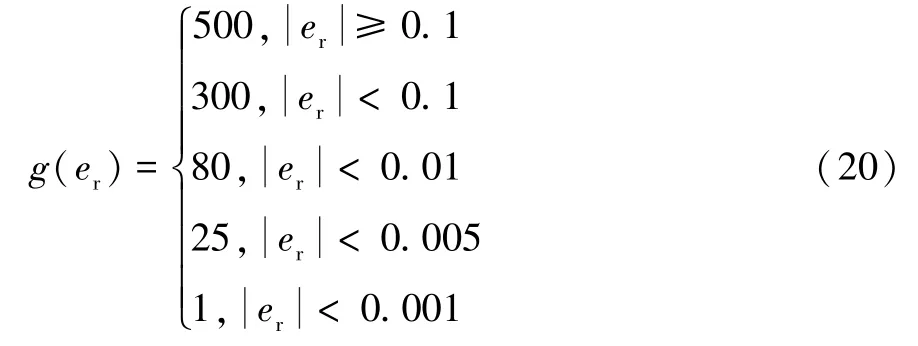
发动机处于地面状态时,使用MATLAB 对基于模糊误差判断算法的PID 控制器进行仿真,时间为10 s。发动机转速阶跃响应曲线(地面状态,模糊PID 控制)如图5 所示。

图5 转速阶跃响应曲线(地面状态,模糊PID 控制)Fig.5 Speed step response curves (ground condition,fuzzy PID control)

发动机处于高空状态时,使用MATLAB 对基于模糊误差判断算法的PID 控制器进行仿真,时间为10 s。发动机转速阶跃响应曲线(高空状态,模糊PID 控制)如图6 所示。

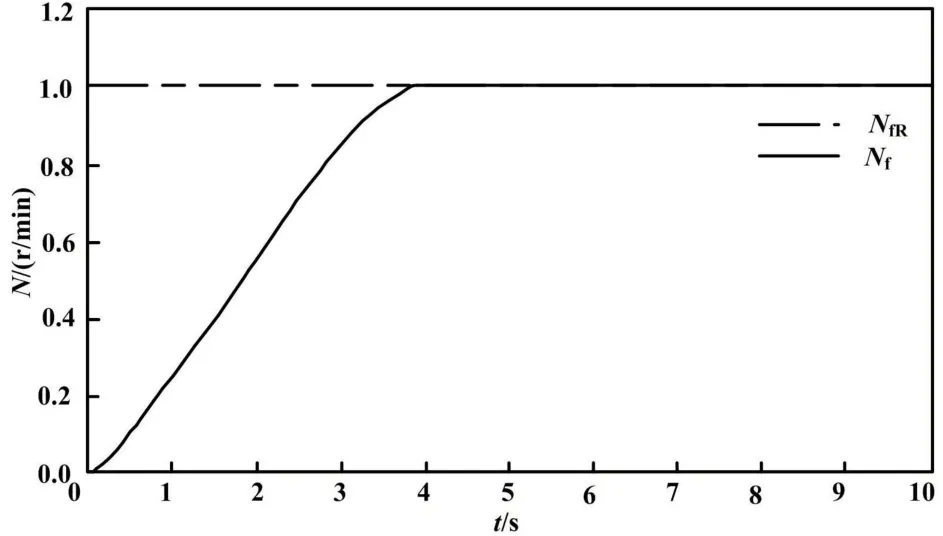
图6 发动机转速阶跃响应曲线(高空状态,模糊PID 控制)Fig.6 Speed step response curves (high altitude condition,fuzzy PID control)

当处于地面状态进行仿真时,采用阶跃激励,涡扇发动机转速达到平稳状态需要用时2.2 s;当处于高空状态仿真时,涡扇发动机转速达到平稳状态需要用时3.9 s。

3 结论

针对PID 控制对航空发动机控制的不足,为了更好地满足对控制方法的需求,本文设计了模糊误差判断PID 控制算法。该算法鲁棒性好、自适应能力强,通过在线快速整定PID 参数,使系统具有响应速度快、控制精度高等特点。与普通PID 控制相比,该方法达到稳定所需用时更短,且无超调量产生。