不同加固措施下竖井式基坑开挖引起的下卧地铁隧道竖向隆起变形规律

刘 波，李海斌,2，李 力，高 伟，黄诚为

（1.中国矿业大学（北京） 力学与建筑工程学院，北京 100083；2.深圳市中地建设工程有限公司，广东深圳 518000；3.深圳市大升高科技工程有限公司，广东深圳 518000；4.深圳市建设综合勘察设计院有限公司，广东深圳 518000；5.华润（深圳）有限公司，广东深圳 518000）

为最大限度利用有限的城市土地空间、不断提升土地开发建设密度和现代地下空间利用程度，部分地下空间建设项目开展时，将不可避免地接近或靠近既有的地下结构，甚至与之产生相互影响。例如，现在已有相当数量的基坑位于既有车站、隧道等地下结构之上。若忽视这种相互影响，那么相应的后续地下空间开发活动，极有可能导致既有地下结构产生过大的竖向或侧向变形，而这无疑将会对地下轨道交通的持续安全运营带来重大隐患。

针对上方基坑工程引起的下卧地铁隧道竖向隆起变形问题，许多学者结合具体工程实例，采用理论分析、数值模拟等方法，分析了基坑开挖活动对邻近隧道的影响以及隧道的变形机理。刘国彬等［1］、Huang 等［2］、陈郁等［3］、Hou 等［4］、刘涛等［5］、黄宏伟等［6］、李家平等［7］、周裕倩等［8］、张正等［9］、刘帅君等［10］分别研究了上海地区基坑工程开挖上跨既有地铁，造成地铁隧道隆起变形的问题；郑刚等［11］分析天津西青道下沉隧道下邻近既有地铁隧道的监测数据，研究了不同施工阶段时地铁箱体及轨道的变形规律及特点；Hu等［12］以广州市某基坑上跨地铁隧道为例，研究了基坑开挖对下卧地铁盾构隧道变形的影响及相应产生的附加应力；李平等［13］结合南京火车站站前广场龙蟠路隧道西段上跨地铁1 号线双线盾构隧道的基坑支护工程，提出了控制盾构隧道隆起的具体措施。由这些研究工作可知，基坑工程设计方案、建设周期、工程地质条件以及与地下轨道线路之间的空间位置关系等都是影响地铁隧道变形问题的重要因素；总结实际工程中控制下卧隧道结构变形的措施，主要包括在隧道上方及四周进行地基加固、布设抗拔桩与结构底板组成门式刚架结构、基坑降水，以及对隧道上方影响范围内土体采用分层分块开挖等。

在基坑开挖卸荷引起下卧隧道竖向隆起变形的理论研究方面，陈郁等［3］、张治国等［14］分别基于明德林解［15］和文克尔地基模型，将既有隧道视为无限长弹性地基梁计算隧道的竖向隆起变形，最终得到基坑开挖引起邻近隧道变形的理论解析解，但研究结果得到的计算式比较复杂，难以在实际工程中应用和推广。目前来看，对于基坑开挖引起的隧道结构变形问题，既有研究在理论解析、数值分析方面还不够精确和简化，类似工程案例的实测数据也不够丰富，相关对比分析成果较少。而鉴于此类问题的重要意义，十分有必要进一步开展相关分析探讨，推导形成合理的求解计算式，并依据实测工程数据和试验进行可靠性验证，为类似工程问题提供更加科学可行的解决思路和途径。

本文依托深圳前海大型地下道路市政工程中约3 km 长的基坑直接放坡明挖工程，针对开挖时位于多条运营和在建地铁线路上方的区段，研究其施工过程中因基坑开挖引起的下卧地铁隧道竖向隆起变形问题。基于文克尔地基模型的加权残值法微分方程，提出简化的隧道竖向隆起变形力学模型；结合项目特点提出保护下卧地铁隧道的竖井式基坑施工加固方案及组合措施；对比、分析未采取任何措施以及逐步施加土体加固、布设抗拔桩-抗隆起板结构体系、降水、竖井分区跳挖4种控制措施得到的5 种工况，探讨各措施对下卧地铁隧道竖向隆起变形的控制效果和变形影响规律；最后通过对比理论值、实测值，以及未采取任何措施与施加全部4种加固措施这2 种工况下的模拟值，验证力学模型的可靠性。

1 工程背景

1.1 工程概况

深圳市前海双界河路、听海路及其地下道路市政工程规划为前海合作区东西向主干道路，其中部分为地下道路。地下道路的主线隧道全长2 900 m，采用明挖施工，基坑开挖深度3.80～11.60 m，平均宽度约60 m，在里程K0+700—K0+900段，隧道及其左右2 侧的1 号和2 号匝道连续上跨地铁1号线、5 号线和11 号线。在基坑开挖前，地铁1 号线和地铁5号线均已完成施工并投入运营，地铁11号线则尚未运营。

地下道路隧道（主线及匝道）与地下3 条地铁隧道之间的平面关系如图1所示。因地铁1 号线采用明挖施工且其施工工艺、断面尺寸与采用盾构施工的地铁5号线、11号线差别较大，本文暂不考虑地铁1 号线的影响，将研究范围限于道路隧道的盾构结构和采用上方竖井式基坑开挖的地铁5号线和11号线。

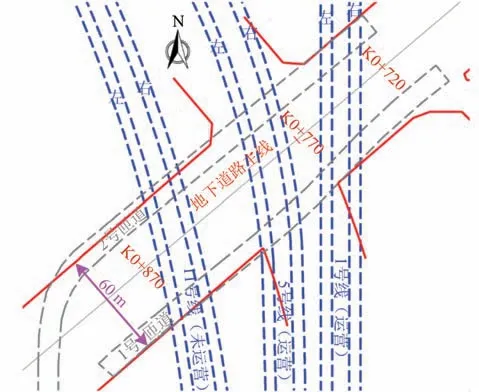
图1 地下道路主线隧道与地铁1 号线、5 号线和11 号线的平面位置关系

盾构地下道路隧道（主线及匝道）与地铁11号线、5 号线的竖向关系如图2所示。上跨11 号线的地下道路基坑深度约6.30～11.60 m，其中2 号匝道坑底最深为11.60 m，与11号线隧道结构顶部的最小竖向距离约3.25 m；上跨5号线的地下道路基坑深度约4.90～6.75 m，其中1 号匝道坑底最深为6.75 m，与5号线隧道结构顶部的竖向最小距离约4.86 m。

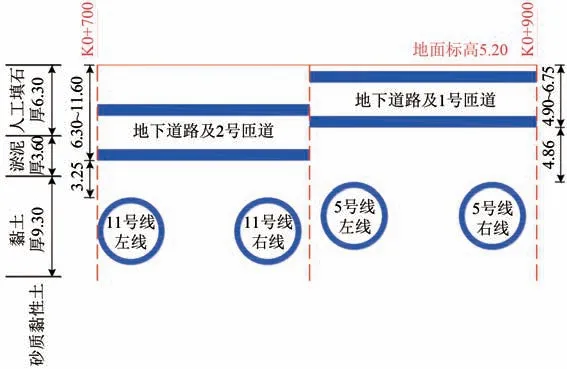
图2 地铁11号线、5号线与地下道路的竖向关系（单位：m）

1.2 工程地质及周边环境条件

本工程位于深圳前海，工程地质及周边环境条件有如下特点。

（1）地质条件差。前海原始地貌为海冲积平原及滨海滩涂，后经填、挖、整平等人工改造形成陆域，场地内填土（石）和淤泥厚度分布极不均匀，极易引起坍塌、土体滑移等风险，稳定地下水位在地面以下约1.0 m，水位较高。

（2）基坑均有一定深度，支护设计难度与开挖风险较大。尤其是地铁11 号线的上方基坑最大深度为11.6 m，属于一级基坑。

（3）基坑上跨地铁隧道，工程施工难度较大且风险性较高。在地铁上方进行开挖施工，会导致地铁上方覆土减少，不仅会引起其原有应力场发生变化、坑底发生竖向隆起变形，同时还会引发地铁隧道管片变形、隧道偏移、整体上浮等诸多问题。

（4）基坑下方的地铁5 号线对开挖活动更为敏感。基坑开挖前，地铁5号线已投入运营，现状调查得知其结构存在局部裂缝，有渗水情况，基坑开挖若引起隧道变形，严重时很可能导致隧道结构涌砂、涌水，造成工程事故。

1.3 地铁隧道变形控制指标

地铁11号线、5号线隧道均为盾构隧道，采用圆形衬砌结构。国家标准CJJ/T 202—2013《城市轨道交通结构安全保护技术规范》［16］规定，隧道结构水平、竖向变形控制值应小于20 mm。深圳市地铁集团发布的《地铁运营安全保护区和建设规划控制区工程管理办法》规定，隧道结构水平、竖向变形控制值应小于10 mm。与深圳地铁运营部门沟通后，考虑到5号线已运营且安全风险较高，其变形控制指标应严格控制不超过10 mm；基坑开挖时11 号线地铁暂未运营且安全风险较低，其变形控制指标可考虑采用国标的20 mm。

2 基坑卸荷引起的下卧地铁隧道竖向隆起变形的力学模型

2.1 基坑卸荷引起的下卧地铁隧道竖向隆起变形机理

一般情况下，大型地下工程项目的数值模拟［17-21］建模工作量巨大。相较于数值模拟，采用理论解直接计算可以节省大量时间成本和精力，更有利于隧道上方基坑卸荷计算在实际工程中的推广，以及在实际工程初步设计预评估中的应用。

基坑开挖卸荷可以等效为在隧道附近基坑深H的位置作用均布荷载p，均布荷载对于其下的隧道结构产生附加应力，进而引起地铁隧道位移。基坑开挖卸荷引起地铁隧道位移变形的机理如图3所示。图中：B为基坑宽度；H为基坑深度；L为基坑长度。根据图3，进一步建立基坑开挖卸荷计算模型的平面投影关系如图4所示。在以基坑底部中心点（0，0）为原点的直角坐标系η-ξ中，隧道中心线上距离基坑中心原点最近的坐标为（η0，ξ0），以（η0，ξ0）为原点对隧道局部建立直角坐标系xy，x'为隧道局部坐标系x-y中隧道中心线上任意1点（x'，0）的横坐标。假设坑底的地铁隧道结构为无限长的均质弹性连续体，则可将其简化为弹性地基梁进行变形计算，并考虑采用附加变形法，研究并确定基坑开挖卸荷引起土体变形的经验式［22］。

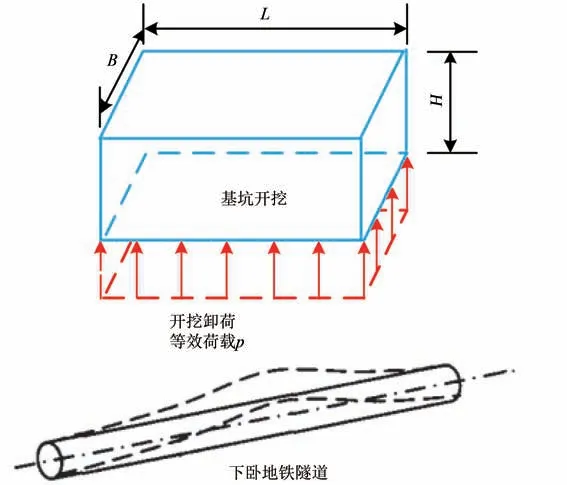
图3 基坑开挖卸荷引起地铁竖向隆起隧道变形机理示意图

2.2 地铁隧道竖向隆起变形力学模型

根据文克尔地基模型，按图4 计算模型求解得出地铁隧道结构的竖向隆起变形微分方程［3，14，22］为

图4 基坑开挖卸荷计算模型的平面投影

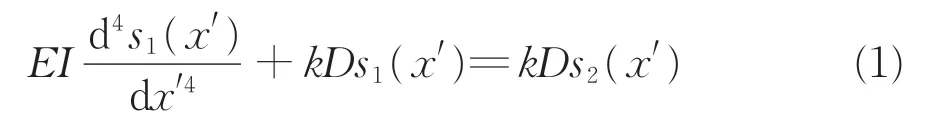
式中：s1(x')为基坑开挖卸荷引起的地铁隧道竖向隆起变形；s2(x')为基坑开挖卸荷引起的土体竖向隆起变形；D为地铁隧道外径；k为基床系数，即地基上任意1 点所受的压力强度与该点处沉降量的比值，在常用土层中取值0.1～50.0 MN·m-3［23］；EI为地铁隧道结构的抗弯刚度。

式（1）的微分方程解［18］为

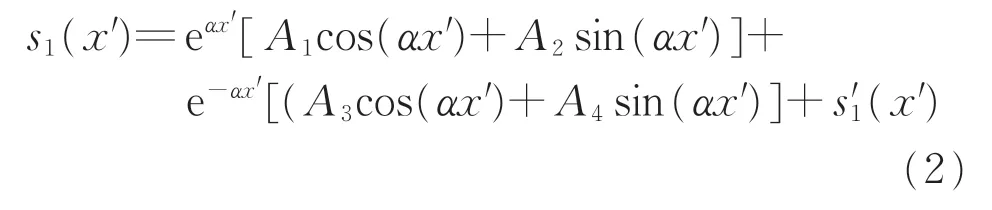
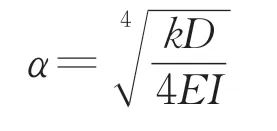
其中，式中：A1，A2，A3和A4为修正系数；α为中间变量；s'1(x')为根据隧道边界条件求解得到的式（1）特解。

将式（1）特解应用于实际工程比较困难，因此考虑将基坑卸荷产生的附加应力变化等效为1 个竖向的集中力F0，即F0=kDs2（x'），再根据边界条件，对式（1）进行数值积分，得到地铁隧道的竖向隆起变形为

如图4所示，设隧道中心线上存在点m，其与隧道局部坐标系原点间的距离为m。在m处作用1个竖向荷载kDs2（m）dm，通过式（3）可以求得该荷载引起隧道中心线上任意1 点（x'，0）的竖向隆起变形ds1(x')为

求解弹性地基梁计算式的微分方程解，即利用式（2）和式（4）积分计算隧道竖向隆起变形比较复杂。为了避免传统明德林应力解方法计算变形时的大量多次数值积分运算，考虑采用附加变形法与加权残值方法相结合的形式进行简化计算。

Peck［24］和O' Reilly 等［25］提出的地基土变形协调方程为

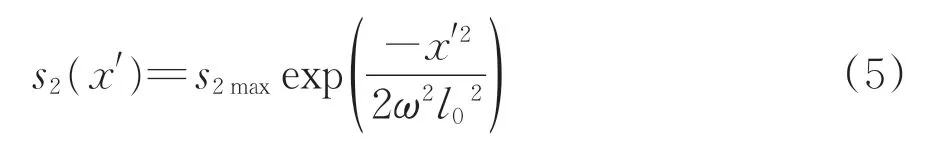
式中：s2max为坑底最大竖向隆起变形值；l0为基坑与地铁隧道间的竖向距离；ω为宽度修正参数，按土质不同，软土取0.7，砂土取0.2～0.3，黏土取0.4～0.5。

将式（5）代入式（1），得到变化后的地铁隧道结构竖向隆起变形微分方程为

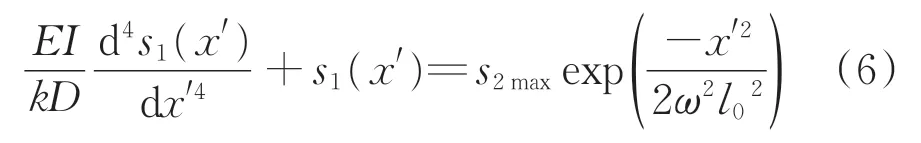
地铁隧道结构的最大竖向隆起变形发生在基坑中心位置，距离中心点无穷远处地铁隧道的位移可假定为0，故式（6）的边界条件为

式中：s1max为地铁隧道结构顶部最大竖向隆起变形，可根据数值模拟结果或者实际监测数据结果确定。

由式（6）直接求微分方程解析解或者数值解均较为困难，因此考虑对其进行简化，求得微分方程近似解。将文献［22］的研究成果与实测数据进行对比，发现式（6）中的四阶微分的数值小到可以忽略。在忽略四阶微分的基础上，将式（7）代入式（6），求解得到微分方程的近似解s1(x')为

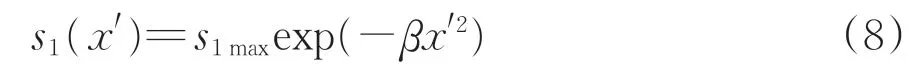
式中：β假设为大于0的变量。

采用加权残值法的狄拉克δ函数（Dirac Delta Function），狄拉克δ函数是1个广义函数，物理学中常用其表示质点、点电荷等理想模型的密度分布，该函数在除零以外的点取值都等于零，定义Xi为

式中：xi为隧道轴线上某1 点与隧道局部坐标系原点的距离；i为正整数。

以式（9）为权函数，当Xi满足x'≠xi时，Xi=0。权函数Xi配点法的加权积分方程为

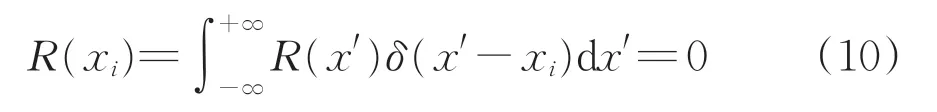
式中：R（x'）为x'为自变量的残值函数；R（xi）为xi为自变量的残值函数。

再将式（8）代入式（6），得到式（6）微分方程的残值函数R（x'）为

将式（11）代入式（10），并令xi=0，得到其加权积分方程为

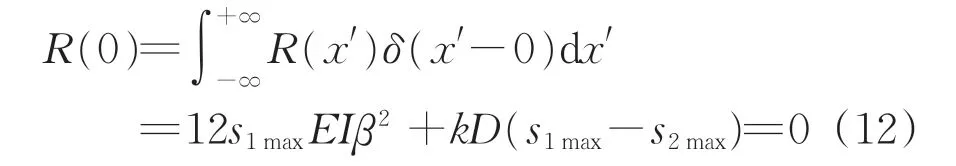
对于式（6）的近似解式（8），其边界条件为β＞0，由此求解式（12），得到β为

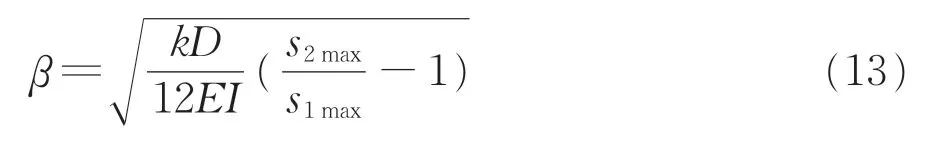
将式（13）代入式（8），得到文克尔地基模型的加权残值法微分方程解，即沿地铁隧道纵向x方向任意1点的地铁隧道竖向隆起变形s1(x')为

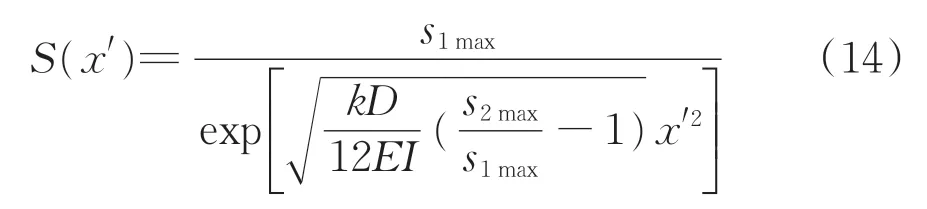
式（14）中的最大竖向隆起变形位移s2max，可根据侯学渊等［26］建立的基坑底竖向隆起变形的经验计算式（15）得到。

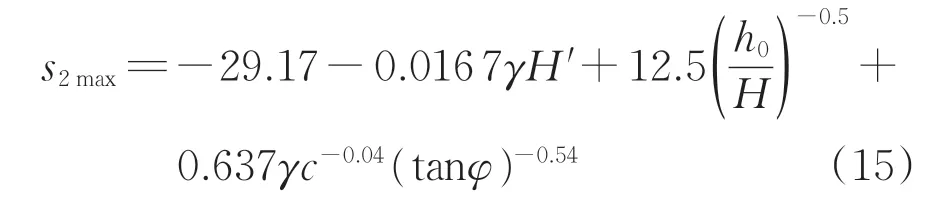
其中，

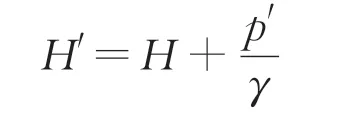
式中：H'为等效基坑深度；p'为基坑顶超载；γ为开挖部分土体的加权平均容重；h0为基坑支护桩（墙）的嵌固深度；c为坑底土层的加权平均黏聚力；φ为坑底土层的加权平均内摩擦角。

对式（2）求导，得到地铁隧道弯矩M(x')的计算式为

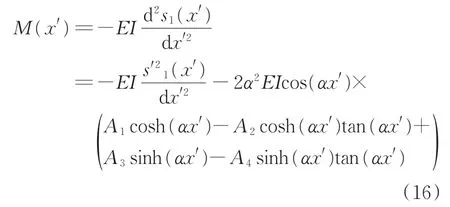
对式（16）求导，得到地铁隧道剪力q(x')的计算式为

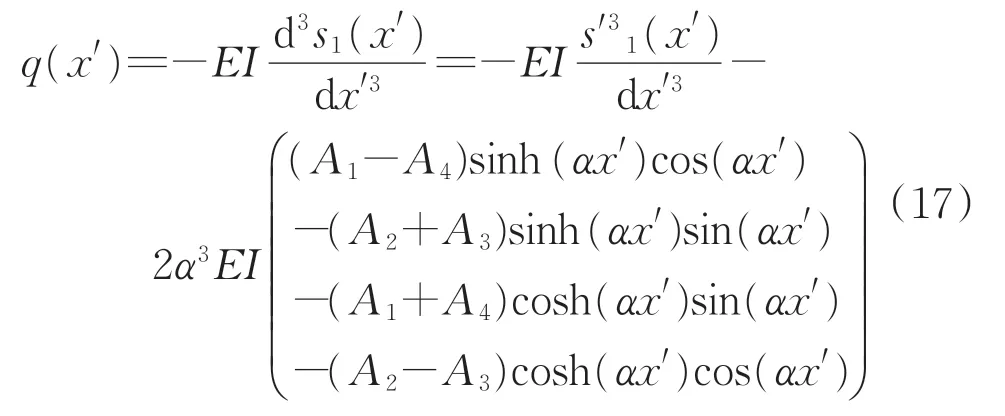
式（16）和式（17）直接求解比较困难，因此考虑采用附加变形法与加权残值方法结合进行简化计算。将式（14）代入式（16）求导，得到地铁隧道弯矩M(x')的计算式为

同理，将式（14）代入式（17）求导，得到地铁隧道剪力q(x')的计算式为

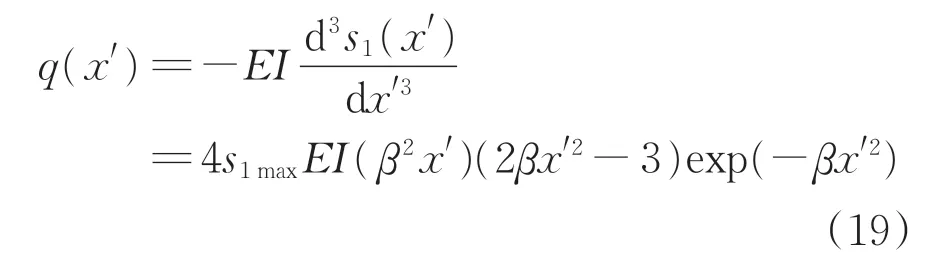
根据式（18）和式（19），即可结合数值模拟得到的隧道最大竖向隆起变形值，计算出基坑开挖引起下卧地铁隧道结构的剪力和弯矩。由此，式（14）、式（18）和式（19）共同组成竖井式基坑开挖引起下卧地铁隧道竖向隆起变形的力学模型，但模型的可靠性，还有待通过数值模拟等形式进一步验证。

3 保护下卧地铁隧道的竖井式基坑施工加固方案

3.1 竖井式基坑施工加固组合措施

结合依托工程特点，参考常用的地铁保护加固措施，提出以下组合措施。

（1）土体加固：采用注浆钢管桩，对地铁隧道上方及2 侧1.5 m 以外区域土体进行加固，坑底以上采用空桩。

（2）抗拔桩-抗隆起板结构体系：对抗隆起板预留注浆孔，通过抗隆起板将抗拔桩、冠梁和连梁连接，形成抗隆起结构体系，如图5所示。

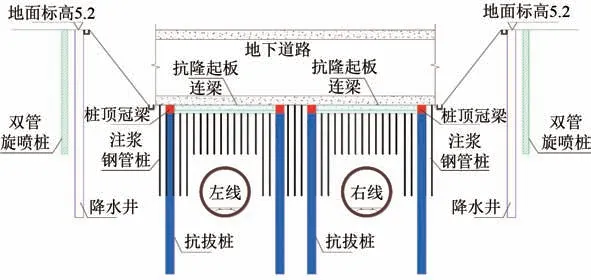
图5 保护下卧地铁隧道的竖井式基坑施工加固方案剖面图（单位：m）

（3）降水：基坑四周施工双管旋喷桩止水帷幕，坑内降水至坑底以下。

（4）竖井分区跳挖：采用竖井分区跳挖的土方开挖方式，开挖到底后及时施工抗拔桩冠梁、连梁和抗隆起板，地铁上方竖井平面图如图6所示，以1#竖井为例，其开挖剖面如图7所示。

图6 地铁11号线、5号线上方竖井平面布置图

（5）待结构达到设计强度后，放坡开挖然后拆除竖井。

（6）边开挖边拆除竖井直至挖至坑底，施工剩余部分抗隆起板结构。

3.2 竖井式基坑的开挖尺寸

合理确定竖井尺寸依据的原则是：在满足施工空间的条件下尽量减少竖井开挖面积。由此，考虑对竖井长边取值为2×（地铁隧道半径+地铁保护最小净距+抗拔桩径+施工操作空间）+施工误差冗余，即2×（3+3+1+0.5）+0.5=15.5 m；考虑对竖井短边取值为大于常用YC35 小型挖掘机（尺寸：长×宽为5.25 m×1.52 m）施工操作空间的最小宽度，即5.5 m。

3.3 竖井施工方法及工序

地铁11号线和5号线的左、右线上方基坑各分为7个竖井（详见图7），为避免相邻竖井在开挖期间相互影响，采用竖井分区跳挖施工的方法。

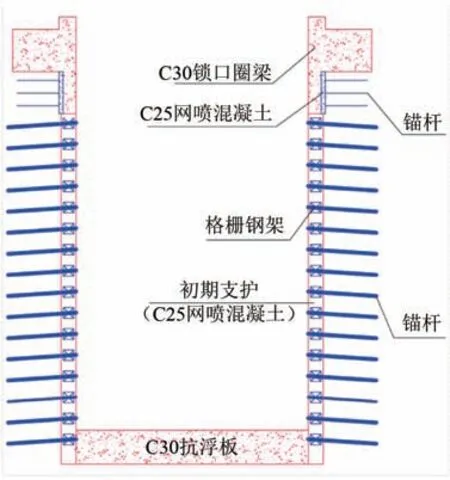
图7 竖井开挖剖面图

以5 号线为例，其具体施工工序为：①开挖基坑，先开挖左线上方基坑，再开挖右线上方基坑，以此类推继续施工；②基坑开挖各分为3 个循环，其中左线竖井开挖顺序为第1 循环1#，5#，第2 循环3#，7#，第3 循环2#，4#，6#，右线竖井开挖顺序为第1 循环8#，12#，第2 循环10#，14#，第3 循环9#，11#，13#。

4 模拟及实测验证

前文建立的力学模型虽然可以得到地铁隧道内力与竖向隆起变形的加权残值解，但这只适用于初步分析或者无任何加固措施的基坑放坡开挖；对于基坑支护结构布置复杂、基坑近接其他地下结构、施工过程中采取了加固措施的情况，则较难通过模型直接得到下卧地铁隧道竖向隆起变形的影响机理。

为此，考虑通过数值模拟与实际监测，研究依托工程基坑开挖时，未采取任何措施及逐步施加施工加固措施后，下卧地铁11号线和5号线的隧道竖向隆起变形规律。

4.1 基坑施工加固工况分类

考虑到滨海软土地区临近地铁隧道的基坑开挖施工具有极高的复杂性与风险性，为合理保护基坑下方的地铁隧道，按前文提出的竖井式基坑施工加固方案，建立未采取任何措施以及逐步施加土体加固、抗拔桩-抗隆起板结构体系、降水、竖井分区跳挖这4种加固措施形成的5种工况如下。

（1）工况1：未采取任何措施。

（2）工况2：仅采取土体加固措施。

（3）工况3：在工况2的基础上，采取抗拔桩-抗隆起板结构体系。

（4）工况4：在工况3 的基础上，采取基坑降水措施。

（5）工况5：在工况4 的基础上，实施竖井分区跳挖的土方开挖方式。

4.2 有限差分数值模型

在基坑开挖施工前，采用FLAC 3D 软件建立三维数值模型，分析基坑及其开挖对地铁11 号线和5 号线隧道影响的三维数值计算网格分别如图8和图9所示。为消除边界效应对计算结果的影响，设模型边界条件为：X方向向外扩约4 倍开挖深度；Y方向向外扩展约4 倍开挖深度；Z方向沿基坑底再向下取约4倍基坑深度。

图8 基坑开挖对地铁11 号线隧道影响分析的三维数值计算网格

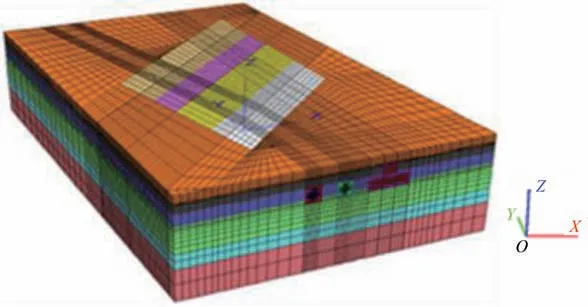
图9 基坑开挖对地铁5 号线隧道影响分析的三维数值计算网格

模拟时，抗拔桩采用pile 单元，抗隆起板采用实体单元，地铁衬砌采用shell 单元，各结构参数均按实际工程尺寸取值，主要结构截面尺寸及物理力学性质指标见表1。

表1 主要结构截面尺寸及物理力学性质指标

数值计算时，土层采用应变硬化弹塑性（strain-hardening）模型，各地层物理力学性质参数见表2。

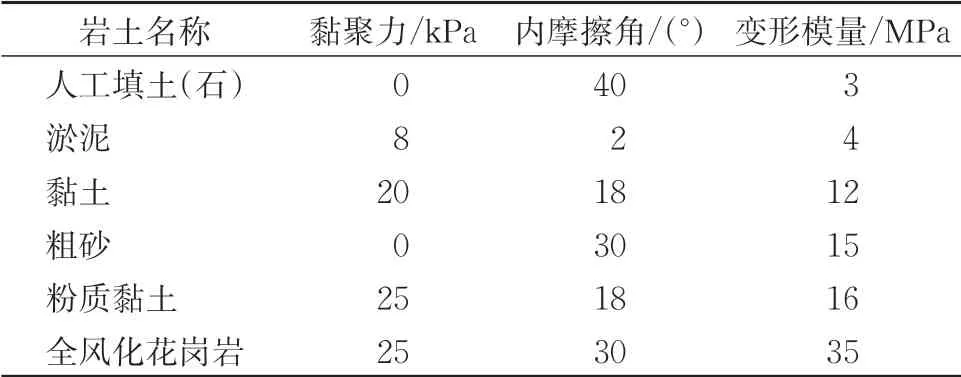
表2 各地层物理力学性质参数

4.3 模拟结果

模拟工况1—工况5，通过工况间的对比，考察土体加固、抗拔桩-抗隆起板结构体系、降水、竖井分区跳挖这4种基坑加固措施对下卧地铁隧道竖向隆起变形的控制效果。不同工况下的地铁隧道竖向隆起变形计算结果见表3。地铁11 号线和5 号线在各工况下的隧道竖向隆起变形云图分别如图10和图11所示。

综合表3、图10和图11，可得出如下结论。

（1）未采取任何加固措施时（工况1），地铁隧道竖向隆起变形远大于允许值，不能满足地铁运营安全要求。工况2—工况5 逐步施加土层注浆加固、抗拔桩-隆起板结构体系、降水、竖井分区跳挖等措施，隧道竖向隆起变形也随之逐步减少，待4 种加固措施施工完毕后（工况5），地铁11 号线、5 号线的最大隆起值分别为17.80 mm 和9.44 mm，均小于地铁竖向隆起变形的最大允许值。

（2）从隧道的最大隆起值来看，地铁11 号线比5号线多8.36 mm，其主要原因是地铁11号线和5 号线上方基坑最大深度分别为11.60 m 和6.75 m，隧道顶距坑底部的最小距离分别为3.25 m 和4.86 m。从空间效应原理上分析，卸荷比（基坑开挖深度/隧道埋深）越大，基坑开挖引起隧道竖向隆起变形也越大，这与文献［12，27］研究结果一致。

（3）由表3 中的地铁隧道变形计算结果可知，对于地铁11号线和5号线的盾构隧道，土体加固措施可减少10%～12%隧道隆起值，抗拔桩-抗隆起板结构体系可减少13%～15%，降水措施可减少3%～5%，竖井分区跳挖措施可减少18%～21%。因坑底为较厚淤泥层、黏性层等渗透系数较小的土层，且基坑止水帷幕位于隧道以上，基坑降水对隧道竖向隆起变形的影响不明显。地铁11 号线上方的基坑开挖较深、地质条件较差，地铁隧道竖向隆起变形对土体卸荷作用比较敏感，故依次采取这些保护下卧地铁的基坑加固措施，可以有效减少基坑卸荷的影响及其范围，其中竖井分区跳挖措施对减少隧道竖向隆起变形的作用最为明显。

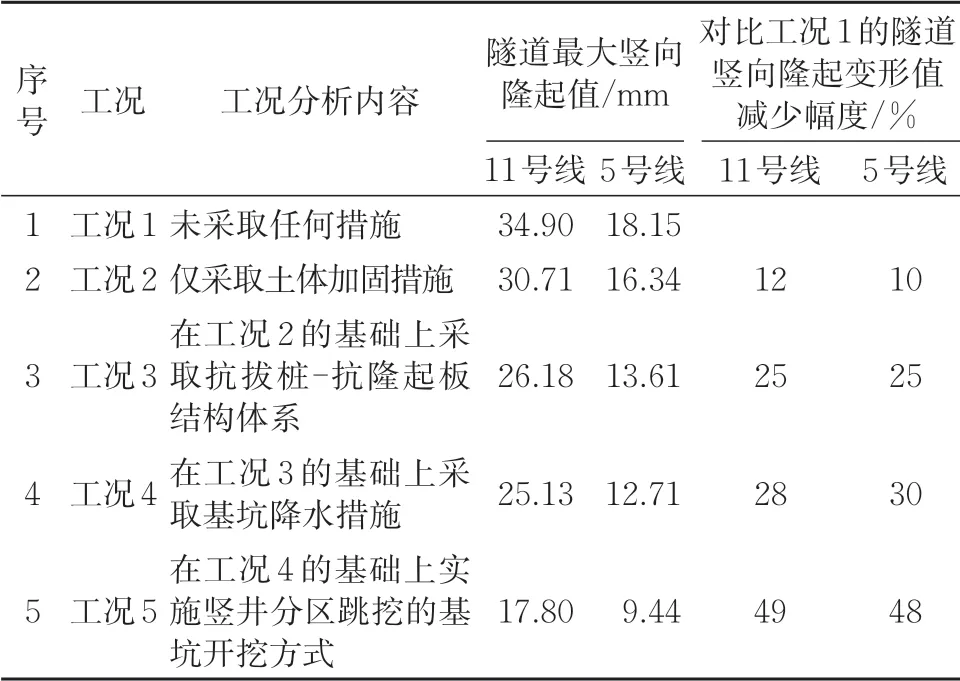
表3 不同工况下的地铁隧道竖向隆起变形计算结果

4.4 对比验证

分别对比理论计算、实际监测、数值模拟3 种方法得到的下卧地铁隧道纵向各断面竖向隆起变形最大值，断面沿隧道纵向按10 m 间距布置，监测范围为3倍基坑深度范围内，其中地铁11号线隧道共布置12 个监测断面，地铁5 号线隧道共布置14个监测断面。

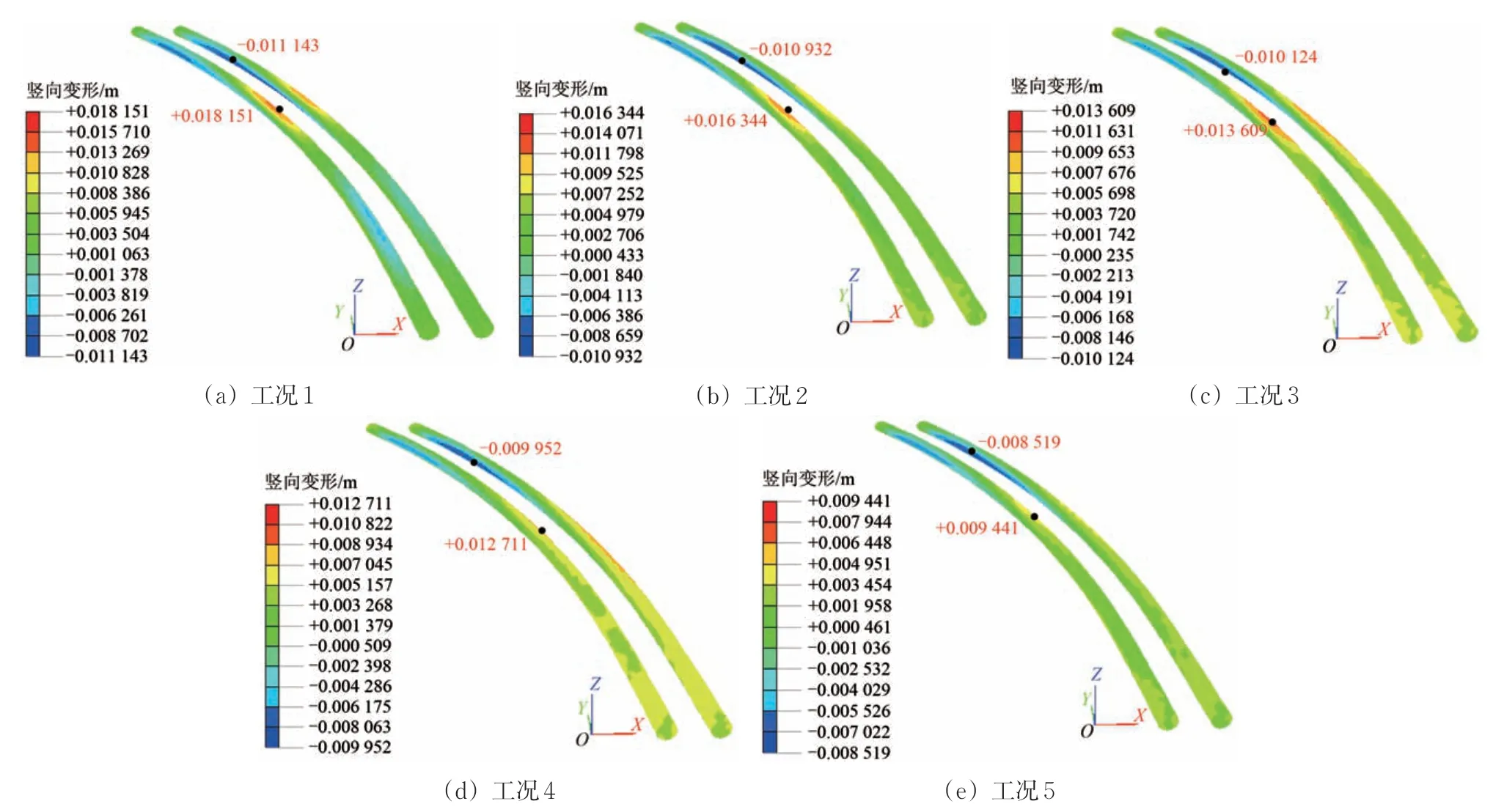
图10 各工况下的地铁11号线隧道竖向隆起变形云图

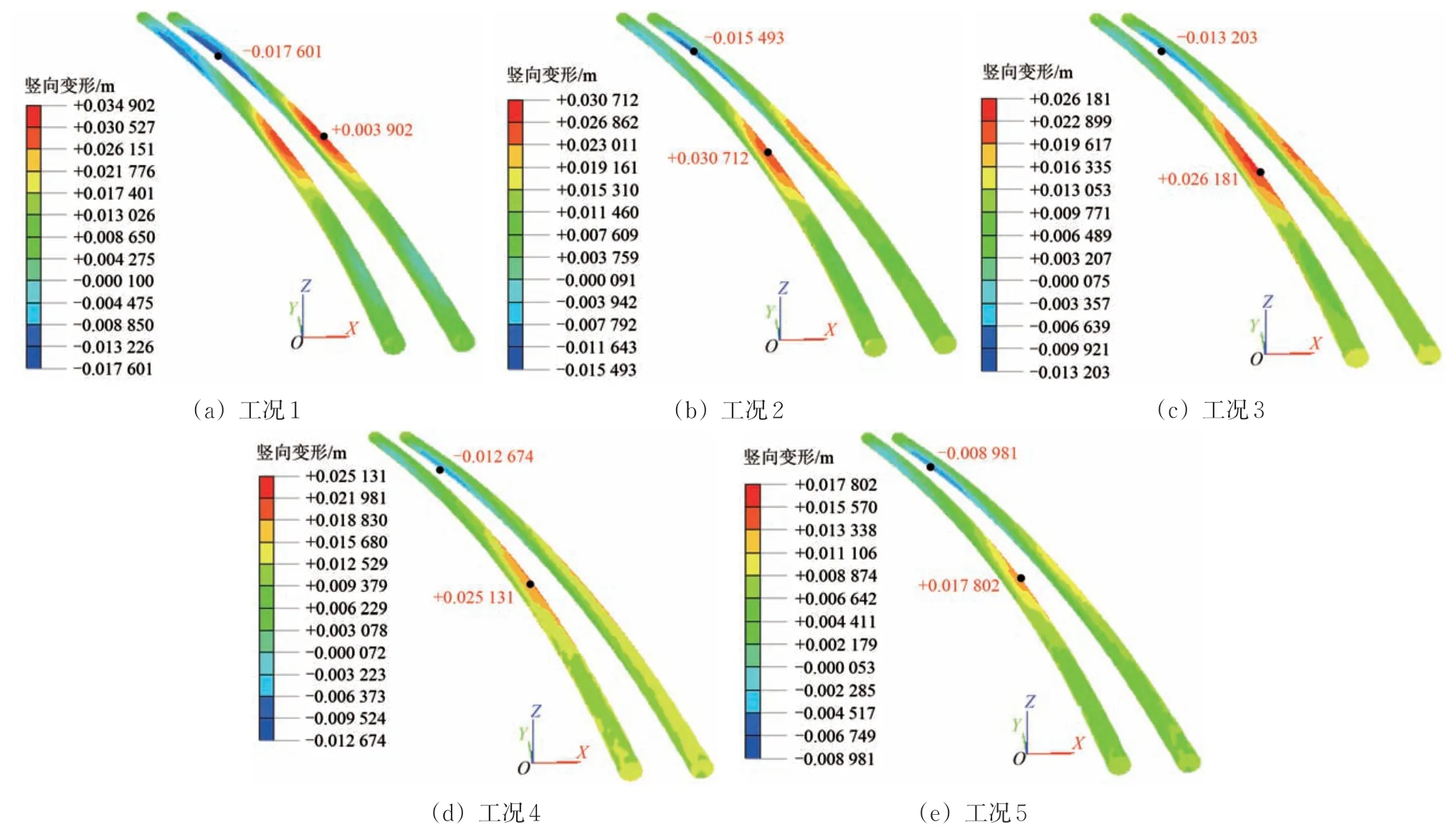
图11 各工况下的地铁5号线隧道竖向隆起变形云图

考虑到理论计算与实际监测的现实情况，理论值仅取未采取任何加固措施时（工况1），实测值仅取施加4种加固措施后（工况5）。限于篇幅，本文仅分析地铁11号线右线与5号线左线的隧道纵向各断面竖向隆起变形最大值，分别如图12 和图13所示。图中：位移起始零值为施工开始的时间点；变形值为正表示向上方变形；粉色虚线为地下道路主线的中心线，黑色虚线为2 条匝道的轮廓线，主线、与2 条匝道的位置关系详见图1。由图12 和图13可得出如下结论。

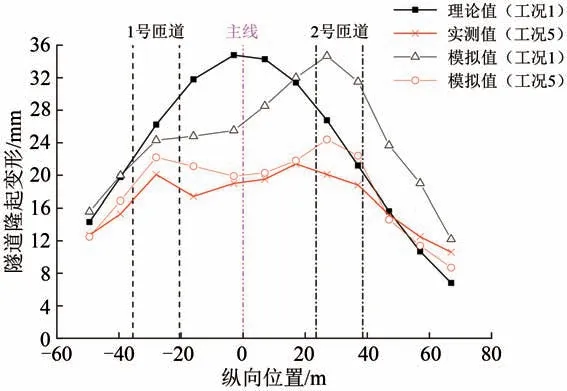
图12 地铁11 号线右线隧道纵向各断面竖向隆起变形最大值计算结果

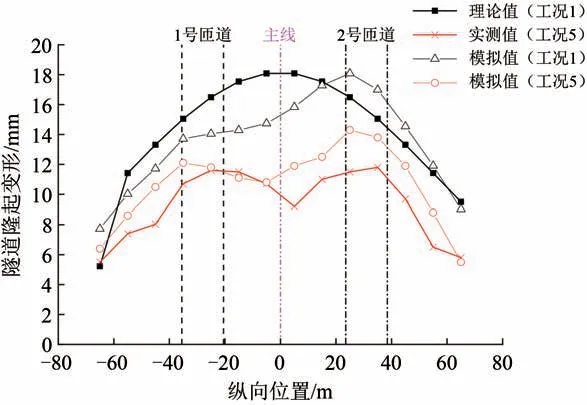
图13 地铁5 号线左线隧道纵向各断面竖向隆起变形最大值计算结果

（1）对未采取加固措施的工况，理论值的变化趋势与实测值基本一致，但在数值上存在差别。各断面下的理论值基本大于甚至远大于实测值和模拟值（工况5），其主要原因是：理论值分析的是未采取任何加固措施的工况1，未考虑实际施工中采用的土层加固、抗拔桩-抗隆起板结构体系、降水、竖井分区跳挖这4 种保护下卧地铁的基坑加固措施，这些措施将有效控制和减少隧道的竖向隆起变形，同时也会导致理论值偏大，这说明本文模型得到的理论值偏于安全。

（2）对于上跨地铁隧道开挖施工的竖井式基坑，由于其上方开挖基坑的深度存在差异，开挖卸荷对隧道竖向隆起变形的影响起主要作用，1 号匝道和2 号匝道的基坑深度明显大于主线道路区域基坑深度，故2 侧匝道处的基坑坑底的竖向隆起变形最大，至2 侧未开挖区域逐渐减小，变形曲线呈“马鞍型”。

（3）模拟值（工况5）的变化趋势与实测值基本一致，但数值上存在一定差别。其主要原因是：①实际工程中，由于部分地层的流变特性和开挖时间效应会对既有隧道变形产生不确定的影响，这部分变形约占最终变形的15%左右［28］，会导致模拟值曲线与实测值曲线存在交点；②因数值模拟时采用淤泥层强度参数为直剪试验值，受土样扰动等因素影响，比原位试验强度参数的取值偏小，导致地铁隧道竖向隆起变形的计算值比实测值偏大，但趋势基本吻合，说明数值模拟结果偏于安全；③当多条地铁线位距离较近时，隧道竖向隆起变形的近似解计算值与实测值存在一定差距，说明其适用性还有待进一步研究和修正。

5 结论

（1）基于文克尔地基模型的加权残值法微分方程，提出简化的隧道竖向隆起变形力学模型。

（2）结合项目特点提出保护下卧地铁隧道的竖井式基坑施工加固方案及组合措施，采用数值模拟验证，对比未采取任何措施以及逐步施加土体加固、抗拔桩-抗隆起板结构体系、降水、竖井分区跳挖这4 种加固措施的工况可知，土体加固措施可减少10%～12%隧道隆起值，抗拔桩-抗隆起板结构体系可减少13%～15%，降水措施可减少3%～5%，竖井分区跳挖措施可减少18%～21%，竖井分区跳挖措施对减少隧道竖向隆起变形最为有效。对于土体渗透系数小且在有隧道位置止水帷幕未封闭的情况，降水措施对减少隧道竖向隆起变形不明显。综合数值模拟与实际监测结果，证明在复杂地质条件下，组合运用这4 种加固措施，可以有效地控制上方基坑开挖引起的下卧地铁隧道竖向隆起变形。

（3）对于上跨地铁隧道开挖施工的竖井式基坑，由于其开挖深度存在差异，开挖卸荷对下卧地铁隧道竖向隆起变形的影响起主要作用，匝道的基坑深度明显大于主线道路区域基坑深度，故2 侧匝道处的基坑坑底竖向隆起变形最大，至2 侧未开挖区域逐渐减小，变形曲线呈“马鞍型”。

（4）通过本文模型对竖井式基坑施工加固方案进行验证，对于未采取任何加固措施的工况，得到的隧道纵向各断面竖向隆起变形理论值曲线趋势与实测值基本一致，但数值上存在一定差别；对于施加4 种施工加固措施的工况，计算结果则偏于安全。

（5）当多条地铁线位距离较近时，本文模型得到的隧道竖向隆起变形理论值与实测值存在一定差距，模型的适用性还有待进一步研究和修正。