不同配筋率下铁路重力式桥墩抗震性能试验研究

2021-06-18鲁锦华陈兴冲丁明波刘正楠张熙胤

中国铁道科学 2021年3期

鲁锦华，陈兴冲，丁明波，刘正楠，张熙胤

（兰州交通大学土木工程学院，兰州 730070）

随着我国铁路建设的高速发展，全国高速铁路线“八纵八横”已基本完成，每条线路中桥梁里程占总线路里程的比例均比较高。桥墩是桥梁结构中非常重要的部件，主要作用是传递竖向力和承受水平荷载。对已有震害的调查发现，桥墩在地震作用下为易损构件，一旦桥墩受损严重，将导致整个桥梁无法使用。因此，保证桥墩有良好的抗震性能对桥梁的安全尤为重要。

自20世纪60年代起，美国、新西兰和日本等国开始对桥墩的抗震性能进行研究。大量的试验研究发现，影响桥墩抗震性能的主要因素有轴压比、剪跨比、配箍率、混凝土强度和配筋率等［1-3］，同时获得了适用于方形截面和圆形截面桥墩的约束混凝土本构模型［4］。铁路桥梁重力式桥墩与公路桥梁墩有很大的不同，截面尺寸大，且只配置护面钢筋，纵向钢筋配筋率多数低于0.5%。配筋率成了影响铁路重力式桥墩抗震性能的主要因素，对此很多学者进行了深入的研究。鞠彦忠等对10 个大比例尺圆端形配筋率为0.1%和0.2%的桥墩模型进行了试验研究，发现配筋率较低的桥墩破坏时均为纵筋拉断，破坏形态均表现出脆性特征，总体耗能较小，随着配筋率的增加，耗能能力也在增强［5-6］，但未考虑轴压比对抗震性能的影响。蒋丽忠等采用正交试验设计方法对配筋率为0.15%，0.45%和0.75%的高速铁路桥墩进行了试验研究，发现随着配筋率的增加，桥墩的滞回曲线越来越饱满，耗能能力增强，刚度增大，承载能力增大，说明增加桥墩的配筋率可以有效地提高桥墩的抗震性能［7］。赵冠远等对配筋率为0.33%和0.74%的高速铁路桥墩进行的试验研究也同样发现，提高配筋率可以有效地提高桥墩的抗震性能［8］。陈兴冲、张永亮等对配筋率小于0.5%的桥墩进行了试验研究，发现随着配筋率的增加桥墩的破坏状态从脆性向延性过度［9-11］。但缺少对其抗震性能的分析。

目前GB 50111—2006《铁路工程抗震设计规范》（2009年版）对配筋率低于0.5%桥墩的抗震设计未做明确规定。从研究现状也可以看出，对于配筋率低于0.5%的铁路重力式桥墩抗震性能的试验研究还缺乏系统性和完整性。为了更为准确地评估低配筋率铁路重力式桥墩配筋率对其抗震性能的影响，需进行大量的试验研究及理论分析。

本文针对低配筋率铁路重力式桥墩，设计制作配筋率从0.2%到0.5%的4 个桥墩模型，研究配筋率对其抗震性能的影响，同时还设计制作了1 个配筋率为1.0%的桥墩模型，对比研究低配筋率桥墩（小于0.5%）与高配筋率桥墩（大于0.5%）抗震性能的区别。

1 模型试验概况

为研究配筋率对铁路重力式桥墩抗震性能的影响，本次试验设计了5 个矩形截面混凝土桥墩，其截面长和宽分别为250 和360 mm，墩高为1 250 mm。各模型桥墩的纵筋选用直径8 mm的HRB335级螺纹钢筋，箍筋均选用直径6 mm 的HRB335 级光圆钢筋，箍筋间距均为102.5 mm，混凝土强度等级为C30，各模型桥墩轴压比均为4%。具体尺寸及配筋构造如图1所示。

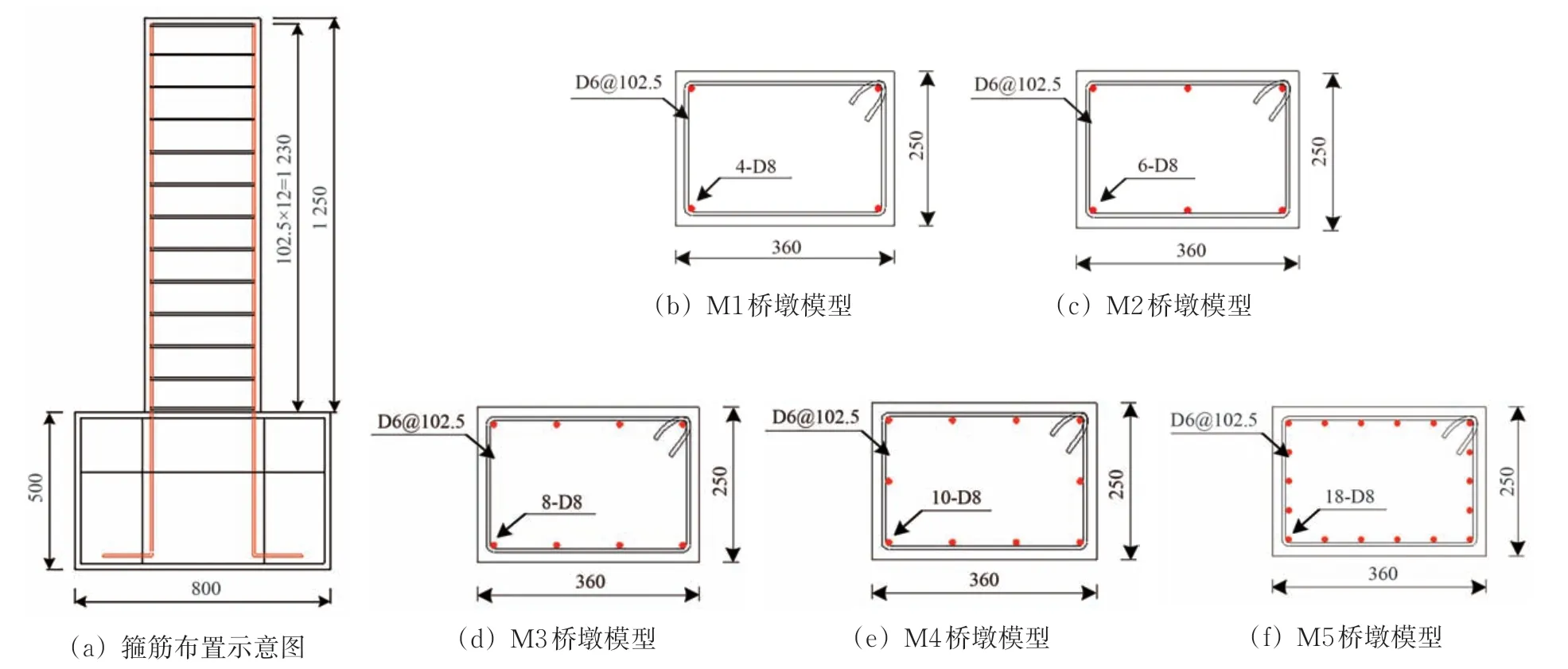
图1 桥墩模型尺寸及配筋构造（单位：mm）

试验加载装置如图2所示，在桥墩上部预埋孔洞处通过液压千斤顶施加低周往复循环荷载。千斤顶的最大加载荷载为300 kN，最大行程为±200 mm。竖向荷载通过墩顶支座上的反力梁和2 根精轧螺纹钢进行施加，在反力梁和精轧螺纹钢之间安装压力传感器，记录施加的竖向荷载。通过计算机控制加载过程，并记录试验加载过程中墩顶施加的荷载和位移。同时根据加载方向在墩底两侧各布置1 个竖向位移计测定钢筋与混凝土之间的黏结滑移位移，实际加载装置如图3所示。

图2 试验加载装置

图3 试验现场实际加载装置图

试验加载制度按照JGJ/T 101—2015《建筑抗震试验方法规程》的规定进行设定，选用力-位移混合加载控制制度。桥墩开裂前采用力控制加载，开裂后采用位移控制加载，从5 mm 开始逐级递增，15 mm 之前增幅为2 mm，15 mm 之后增幅为5 mm，每级加载3 次。当水平荷载下降到峰值荷载的85%以下或者钢筋拉断时，认为桥墩达到极限破坏状态，停止加载。

2 试验结果

2.1 试验现象

各桥墩模型的最终破坏状态如图4所示。

图4 桥墩模型最终破坏状态

除M5 桥墩模型外，其余4 个桥墩模型的最终破坏状态基本一致。力加载控制下，随着配筋率的增加，M1，M2，M3，M4 桥墩的开裂荷载从12 kN 增大到18 kN。桥墩模型开裂后改用位移控制加载，墩顶水平位移加载到5～10 mm 时，4 个桥墩模型墩底4 个面均出现横向裂缝，墩底截面形成贯穿裂缝。随着加载位移的增大，裂缝数量沿墩身向上不断增多，且配筋率越小的桥墩裂缝的数量越少。当加载位移达到30～40 mm时，墩身不再出现新的裂缝，墩底裂缝张开明显。桥墩模型破坏时均是纵向钢筋拉断，水平承载力突然下降，失去承载能力，且墩底混凝土无明显剥落现象，没有表现出延性破坏的特征。

由于M5 桥墩模型配筋率较高，开裂荷载有明显提高，达到了27 kN。加载初期破坏模式同配筋率较少的4个桥墩模型基本一致，只是产生的裂缝数量更多，沿墩身分布更密更宽。破坏阶段，M5桥墩模型墩底混凝土剥落严重，高度达到170 mm左右时，形成了明显的塑性区域，表现出延性破坏特征，这完全不同于配筋率低于0.5%的M1，M2，M3，和M4桥墩模型的最终破坏状态。

2.2 滞回曲线

试验测得的墩顶水平力与位移的滞回曲线如图5所示，图中ρ为配筋率。通过对比可以看出如下规律。

图5 桥墩模型滞回曲线

（1）加载初期，混凝土未开裂，滞回曲线基本呈线性变化，且无残余变形，桥墩模型处于弹性阶段。混凝土开裂后，随着加载位移的增大，桥墩模型损伤加剧，滞回曲线的斜率逐渐减小，刚度逐渐降低，桥墩模型进入弹塑性阶段。同一级加载位移循环下，第1 次加载时的墩顶水平荷载最大，且后1 次均小于前1 次加载时的水平荷载。加载后期，水平荷载均出现突然下降的情况，除M5 外其他各桥墩模型均是因钢筋拉断而失去承载能力。所有试件的滞回曲线均有不同程度的“捏缩”现象，主要是由钢筋与混凝土之间的黏结滑移及加载过程中裂缝未及时闭合造成的。

（2）随着配筋率的增加，桥墩模型的水平荷载不断增大，滞回曲线的“捏缩”效应减小，越来越饱满，卸载后残余位移越大。配筋率从0.2%到0.5%的桥墩在钢筋拉断前，水平荷载几乎没有出现明显的下降，而在钢筋拉断的瞬间，水平荷载突然下降，桥墩失去承载能力；配筋率为1.0%的桥墩在破坏前，水平荷载已经出现下降，且缓慢下降到峰值荷载的85%以下。

2.3 骨架曲线

骨架曲线是指拟静力试验中每级加载的最大荷载与加载位移的曲线，可以直观地反映桥墩模型的承载能力和变形等变化规律。不同配筋率下试件的力-位移骨架曲线如图6所示。

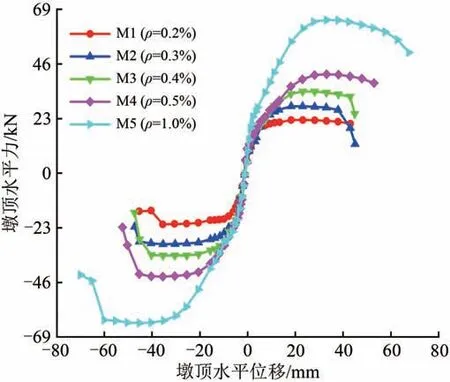
图6 桥墩模型骨架曲线

由骨架曲线对比分析可知：

（1）根据试验结果可将骨架曲线分成3个阶段：①弹性阶段，该阶段墩顶水平位移较小，水平荷载与加载位移基本呈线性增长关系；②屈服强化阶段，随着加载位移的增大，墩顶水平荷载不断增大，由于裂缝的发展和钢筋的屈服，增长速率不断降低，同时试件的刚度也在不断下降；③缓慢退化阶段，配筋率小于0.5%的试件，水平荷载达到峰值之后承载能力几乎无明显下降，直到纵向钢筋拉断才出现突变，而配筋率为1.0%的试件，峰值荷载之后随着加载位移的增大，承载能力不断下降，直到峰值荷载的85%以下，试验停止。反方向加载出现水平荷载突降是由于混凝土剥落严重的原因。

（2）随着配筋率的增加，试件的水平荷载有明显的增加，说明提高配筋率可以有效地提高桥墩的承载能力。

3 桥墩抗震性能

3.1 刚度退化

刚度是指桥墩在地震作用下抵抗变形的能力。桥墩的刚度退化主要是由于混凝土开裂及钢筋屈服造成的。从桥墩的力-位移曲线图中可以明显看到，桥墩的刚度随着加载位移的增大而减小。为了能直观地反映桥墩刚度在循环荷载下的变化情况，引入了割线刚度Ki的概念，具体计算为

式中：±Fi代表第i次加载循环荷载下的正、反方向最大荷载；±Δi为峰值荷载对应的位移。

分析得到不同配筋率下桥墩刚度的退化曲线如图7所示。由图7 可以看出：各试件的刚度退化规律基本一致，退化曲线均呈反比例函数；加载前期，刚度退化速率较快，随着加载位移的增大，刚度退化速率逐渐减小，曲线变化趋于平缓；各试件的刚度退化规律随着配筋率的增大不发生变化，但是相同加载位移下刚度随配筋率的增加而增大。说明提高配筋率可以有效提高桥墩的刚度，增强桥墩在地震中抵抗变形的能力。

图7 桥墩刚度退化曲线

3.2 位移延性系数

目前计算位移延性系数常用的方法主要有纵向钢筋首次屈服法［12］、Park 法［13］、能量等效法［14］和通用屈服弯矩法4 种。第1 种方法可以通过理论计算确定桥墩的屈服位移，后3 种方法类似，均是通过等效的方法确定屈服位移。下文主要采用第1种方法和第3 种方法计算低配筋率铁路重力式桥墩的位移延性系数。

首次屈服法计算桥墩屈服位移时是通过纵向钢筋发生屈服时截面的曲率，按式（2）计算得到。

其中，

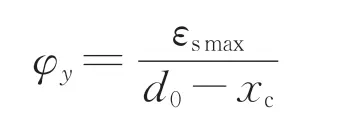
式中：Δy为桥墩屈服位移；φy为桥墩屈服曲率；h为桥墩有效高度；εsmax为纵向钢筋的屈服应变；d0为截面的有效高度；xc为中性轴距离混凝土受压侧边缘的距离。

采用能量等效法计算桥墩的屈服位移时，采用图8所示的屈服位移计算示意图。图中：Fmax为峰值荷载；Δmax为峰值荷载对应的位移；Fy为屈服荷载。

图8 屈服位移计算示意图

用双折线ODE代替原来的力-位移曲线，使SODEF的面积与SOABCEF的面积相等，根据面积相等，可以计算出桥墩的屈服位移和屈服荷载，具体计算公式如下。

取峰值荷载的85%对应的位移为极限位移Δu，未下降到峰值荷载的85%时取加载位移的最大值为极限位移。位移延性系数定义为规范［12］中位移延性系数采用的是“首次屈服位移延性系数”，所得到的位移延性系数再考虑2.5倍的折减系数，作为容许位移延性系数，本文为了与规范进行衔接，也采用“首次屈服位移延性系数”，通过该系数计算得到桥墩模型的容许位移延性系数。表2给出了各桥墩模型采用2 种方法计算得到的屈服位移、极限位移和延性系数。

表2 位移延性系数

从表2 中可以看出：桥墩模型采用能量等效法得到的位移延性系数随着配筋率的增加逐渐减小。而从桥墩模型的破坏特征来看，随着配筋率的提高桥墩发生塑性破坏的区域越大，极限位移逐渐增大，变形能力逐渐增强，延性性能越来越好，这与采用能量等效法计算得到的位移延性系数相悖，但是与采用首次屈服法计算得到的容许位移延性系数变化规律一致。因此，对于配筋率较低的铁路重力式桥墩，建议采用首次屈服法计算桥墩的容许位移延性系数。

3.3 耗能能力

桥墩的耗能能力是指桥墩在地震作用下发生塑性变形而耗散能量的能力，是评价桥墩抗震性能的重要指标。工程抗震设计中一般采用累积耗能定量评定桥墩耗能能力的强弱。各桥墩模型的累积耗能随位移变化的曲线如图9所示。

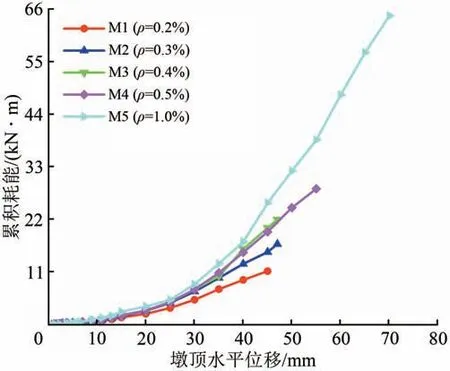
图9 桥墩累计耗能曲线图

由图9 可以看出：加载初期，桥墩模型的损伤较小，不同配筋率下桥墩模型的累积耗能相差较小；随着加载位移的增大，桥墩模型损伤加重及钢筋屈服，不同配筋率下试件的累积耗能相差较大，且配筋率越小，相同加载位移下试件累积耗能差值越大；随着配筋率的增加，试件的累积耗能越大，说明提高配筋率可以有效地提高桥墩的耗能能力。

3.4 黏结滑移位移

钢筋与混凝土之间的黏结滑移位移主要是由于钢筋在混凝土中受到拉力作用时而产生变形，该变形导致了钢筋与混凝土之间发生相对滑移［15］。具体表现在墩底与承台连接处裂缝的宽度，试验中通过墩底加载方向布置的2 个竖向位移计测试墩底抬升的高度，随着墩顶位移的增加，黏结滑移位移如图10所示。

图10 桥墩黏结滑移位移

由图10 可以看出：试件的黏结滑移位移随着配筋率的提高而减小，随着加载位移的增加基本呈线性增加；当配筋率小于0.5%时，试件的配筋率每增加0.1%，相同加载位移下黏结滑移位移变化较大，而当配筋率大于0.5%时，配筋率为0.5%的试件和配筋率为1.0%的试件相比，黏结滑移位移只在破坏阶段相差较大，破坏阶段之前相差较小。说明当配筋率小于0.5%时，配筋率对桥墩的黏结滑移位移影响较大。