基于改进变学习率神经网络的风电机组故障预测研究

陈思羽，王国新，张冬妮

(黑龙江科技大学 电气与控制工程学院，哈尔滨150022)

0 引 言

传统的风电故障检测是先通过Relief算法对风电系统数据进行特征参数权重计算，然后通过权重系数排名选择适当的参数，利用BP神经网络对当前传感器采集的各种数据进行分类，通过传统的神经网络进行非线性映射[1]。由于传统的BP神经网络参数众多，计算和训练过程缓慢，在大型风电机组中因为参数繁多使得训练时间更加缓慢，所以改进优化方法或者使用其它网络结构就变的尤为重要，此前文献[2]和文献[3]中运用的个体变学习率和整体变学习率算法由于算法比较简单，存在一定优化空间。通过对个体和整体变学习率的算法进行优化调整，以达到更快的收敛速度和更短的训练时间。将优化后的改进BP神经网络应用于风电机组故障预测，通过试验证明该算法在风电机组故障诊断中具有较好的适用性，与传统方法相比进一步减少了训练时间。

1 BP神经网络原理

在机器学习中，神经网络算法是基础，其结构如图1所示。

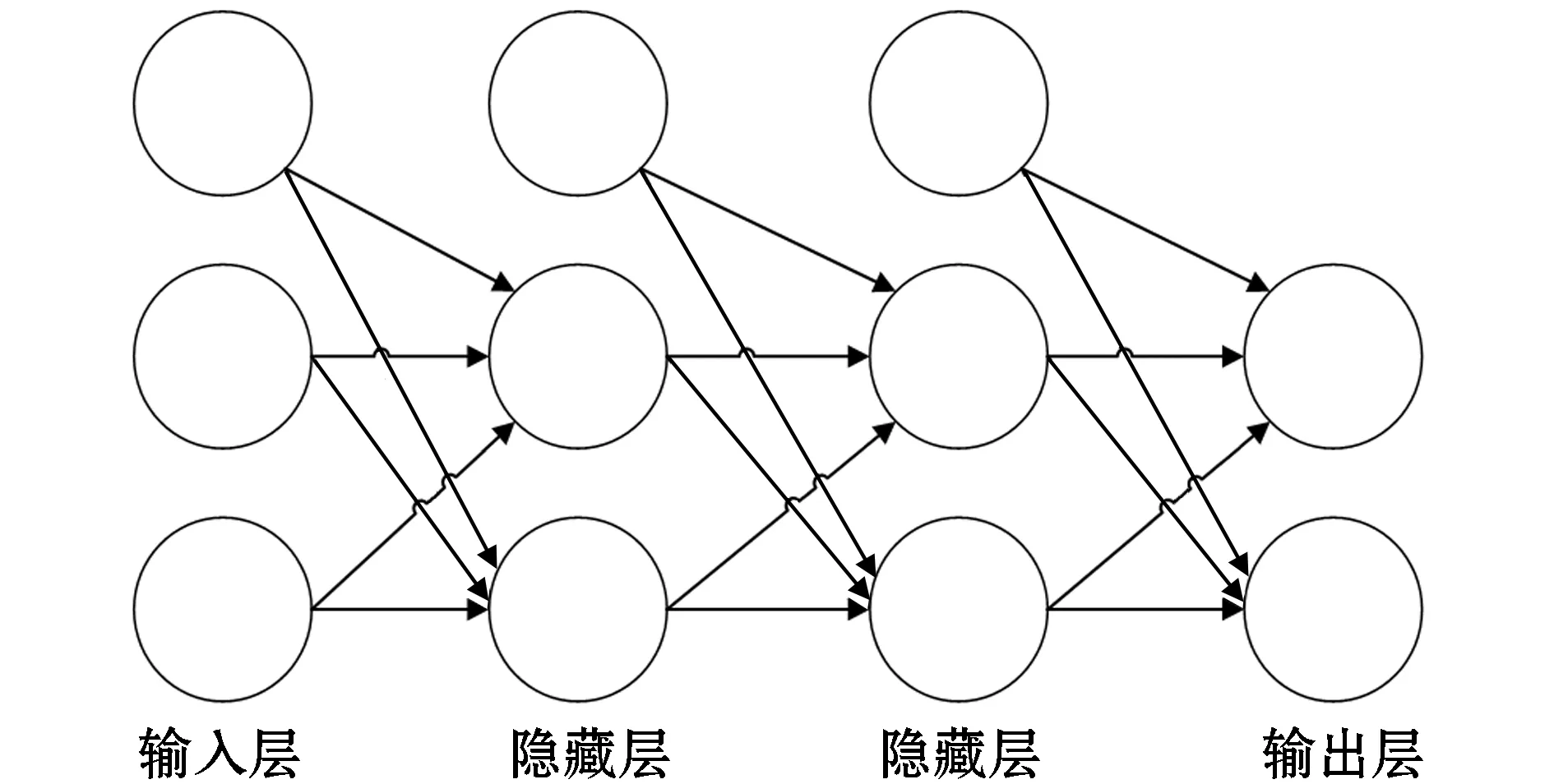
图1 BP神经网络结构

BP神经网络由输入层、隐藏层和输出层组成[4]，其运算过程主要分为前向传播和反向传播。前向传播是输入层通过输入样本x及参数w(1)、b(1)到隐藏层[5]，求得z(1)，进而求得a(1);再将参数w(2)、b(2)和a(1)一起输入输出层求得z(2)，通过激活函数求得a(2);最后得到损失函数L(a(2),y)这个过程称为前向传播，图2为前向传播示意图。训练过程中计算误差和实际误差的差值称为损失函数。在训练过程中需对损失函数进行梯度下降计算，在此计算过程中需要从后往前依次求各个参数的偏导即反向传播。

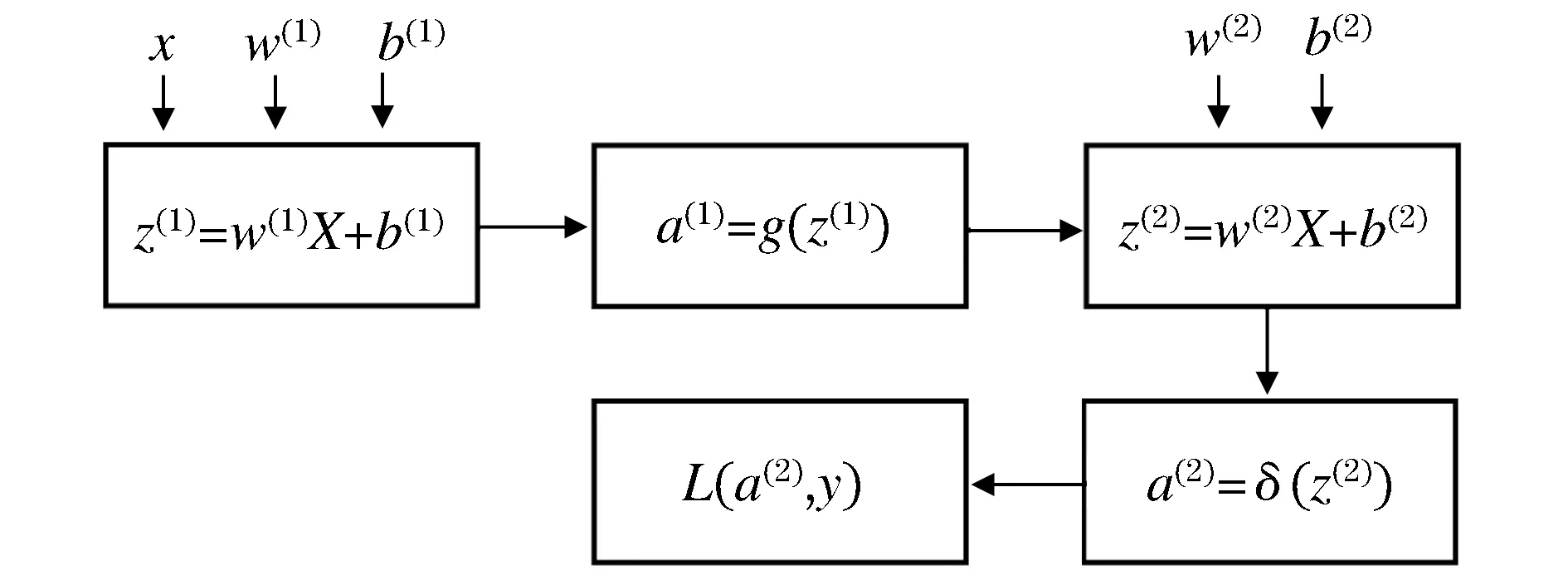
图2 前向传播

前向传播过程：

z(1)=w(1)C+b(1)

a(1)=g(z(1))

z(2)=w(2)a(1)+b(2)

a(2)=σ(z(2))=sigmoid(z(2))

L(a(2),y)=(y-1)log(1-a(2))-yloga(2)

sigmoid函数的导数为

反向传播过程：

=dz(2)·w(2)×g′(z(1))

=dz(1)·XT

2 改进变学习率算法

虽然文献[1]和文献[2]针对BP网络训练慢的问题提出个体变学习率算法和整体变学习率算法，但是变学习率算法仍然存在优化和改进空间，因此提出变学习率算法的改进方法。

2.1 变学习率算法

2.1.1 个体变学习率

输入层与隐藏层的权值矩阵用符号aij来表示，学习速率矩阵设为η，则权值aij所对应的学习率为ηij[6]。aij(n)为权值aij经过n次迭代后得到的值，则ηij(n)对应的学习率是aij(n),E(n)是第n次迭代后得到的全局误差。现有的个体变学习速率迭代式为

2.1.2 整体变学习率

隐藏层与输出层的权值矩阵为bjk。η是初始学习速率矩阵，范围为[0,1],η(n)代表第n次的学习速率，E(n)代表第n次迭代的全局误差。整体学习速率的动态调节规则为

2.2 改进变学习率算法

由于现有变学习率算法不够完善，因此提出一种改进变学习率算法，用两次迭代的代价函数差值的正负决定步长变化项的正负，结合差值的大小，确定步长的变化幅度。变化的步长使用代价函数差值的对数值作为变化的倍数，当系统快速收敛时，快速调整系统的学习速率，当系统缓慢收敛时，缓慢调整系统的学习速率，以增加收敛速度，减少振荡的可能性。

2.2.1 改进个体变学习率

改进的个体变学习率算法将输入层与隐藏层的权值矩阵设为aij，学习速率矩阵设为η，则权值aij所对应的学习率为ηij。aij(n)为权值aij经过n次迭代后得到的值，则ηij(n)对应的学习率是aij(n),E(n)是第n次迭代后得到的全局误差。Sde为步长调节系数，改进变学习率调节方法为

η(n+1)=η(n)+lg(E(n)-E(n-1)+1)×Sde

当第n次迭代的误差E(n)小于第(n-1)次的迭代误差时，代表系统收敛，则学习率增量为正，(n+1)次的学习速率等于η(n)加上正数，则学习率增大，反之学习率减少。这样反复调节aij的学习速率，直至全局误差小于目标值。

2.2.2 改进整体变学习率

隐藏层与输出层的权值矩阵用符号bjk表示，η为其初始学习速率矩阵，其取值范围是[0,1]，η(n)代表第n次的学习速率，E(n)代表第n次迭代的全局误差。改进整体学习速率的动态调节规则为

η(n+1)=η(n)+lg(E(n)-E(n-1)+1)×Sde

当第n次迭代的误差E(n)小于第(n-1)次的迭代误差时，代表系统收敛，则学习率增量为正，(n+1)次的学习速率等于η(n)加上正数，则学习率增大，反之学习率减少。这样反复调节bjk的学习速率，直至全局误差小于目标值。

对于阈值矩阵也采用上述方法进行调节。

3 改进变学习率算法风电故障检测

3.1 数据特征描述

风电机组运行过程中的主要参数包括功率因数设定值、机航位置、塔架加速度、传动系统加速度、机舱旋转等[7]，需将各参数数据整理为数据库格式并清楚标记出故障数据。由于参数众多，这里使用Relief算法对原始数据的参数进行权重计算，通过排名选择特征参数权值排名较高的参数。表1为权重计算后权重大小排名前10名的参数。

表1 特征参数权重排名Table 1 Weight ranking of characteristic parameters

经过Relief筛选后的风电机组运行数据具有一定的物理意义，由于各参数单位之间的差异性，使得各项参数在数值大小上具有很大的差异，为防止一些数值较小的参数被数值较大的参数湮灭，就需要对参数进行归一化计算，将其折算到[0,1]区间内。

3.2 风电故障预测的数学建模

3.2.1 数据预处理

风电系统运行状态量有140个，通过Relief算法将其缩减为50个，并对其进行归一化计算。其数学表达式如下：

Xop=normalize(Relief(Xorg))

式中：Xorg为从风电机组管理系统中直接获得的维度为140的风电机组状态量；normalize(x)为归一化算法；Xop为经过预处理后的状态量。

3.2.2 神经网络选择及其数学模型

测试网络使用50输入、1输出、10个隐节点的神经网络，其输出函数表达式为

式中：bn为隐藏层到输出层的偏置值；B为输入层到输出层的偏置值；Wn为输入层到输出层权值；win为隐藏层到输出层权值；tansig函数为测试网络的隐层传递函数。

3.2.3 目标函数

定义神经网络损失函数的数学表达式：

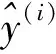
3.2.4 数学模型的求解

风电故障检测为分类问题，网络模型的代价函数值越小越好，其数学表达式如下：

(1)

数学模型求解的目标是对神经网络的权值矩阵进行优化。在不满足收敛判定条件和最大训练次数限制的情况下，持续进行梯度下降迭代。式(1)中第三项为最大训练次数限制，第二项为收敛判定条件。

3.3 训练结果对比及说明

图3为标准BP神经网络误差随训练循环次数变化曲线，可以看出，当迭代次数达到1 000次(最高循环次数限制)时达到最小误差。

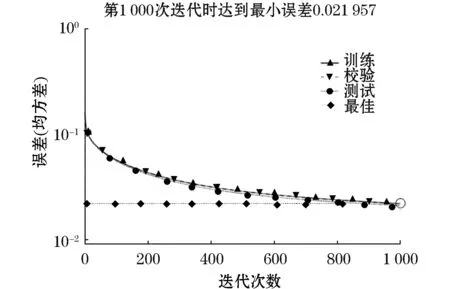
图3 标准BP神经网络误差

变学习率BP神经网络的代价函数值与训练次数之间的关系如图4所示，当迭代次数达到125次时代价函数值最小，与标准网络相比训练次数大幅度减少。

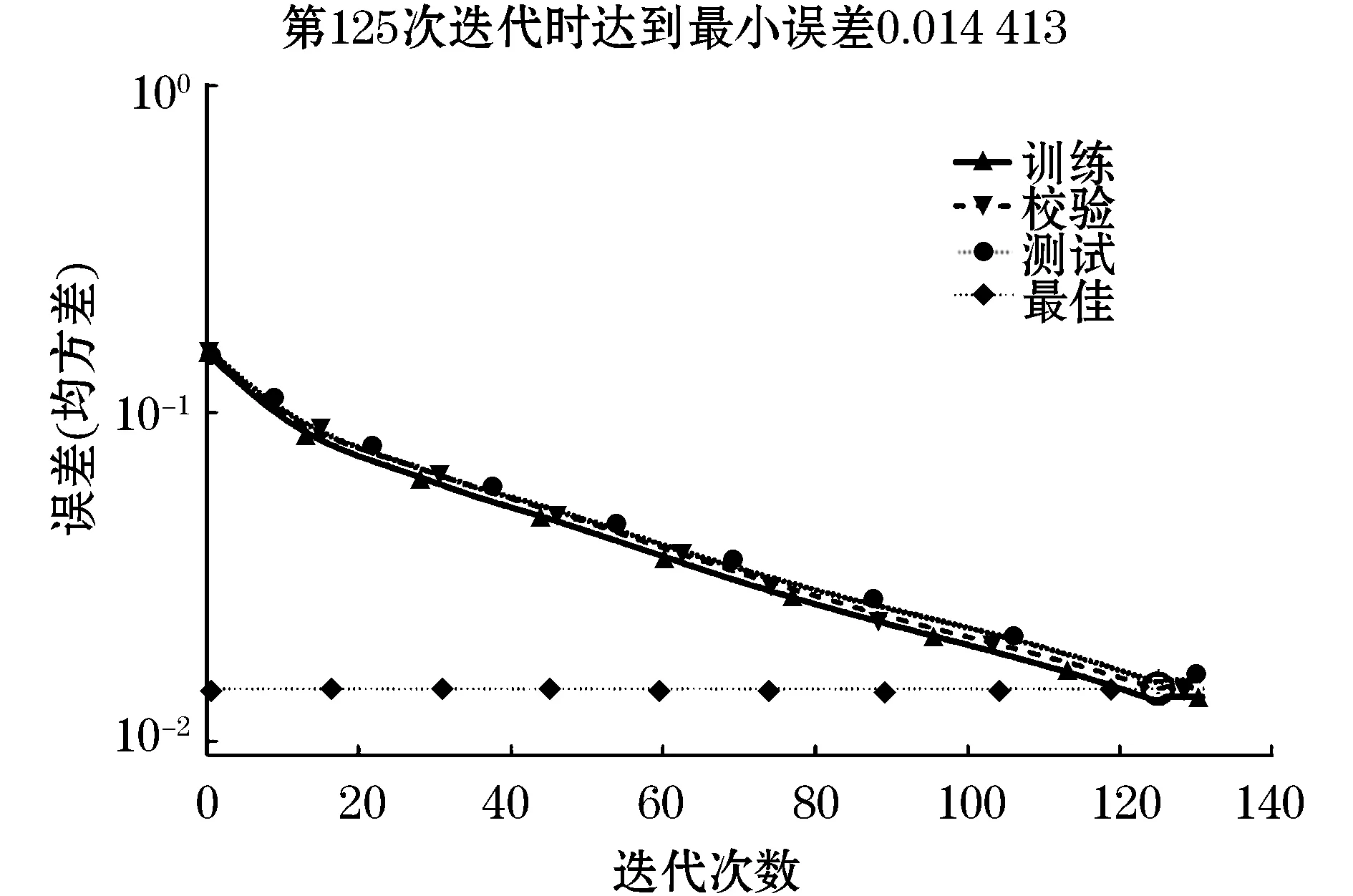
图4 变学习率BP神经网络误差

算法改进后的变学习率BP神经网络误差和迭代次数之间的关系如图5所示，该网络误差在第93个循环时达到最小，相比变学习率BP神经网络训练减少32个周期。

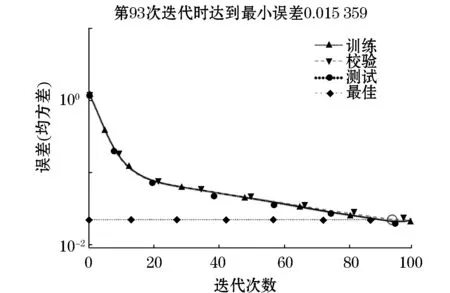
图5 改进变学习率BP网络误差

标准网络、变学习率网络和算法改进后的变学习率网络训练结果对比如表2所示。与变学习率网络相比，改进变学习率网络训练循环次数减少27%，虽然训练精度略有下降，但改进变学习率网络明显缩短了模型训练时长，提升了效率。综合分析训练结果得出改进后的算法适合对训练速度要求较高而对于训练精度的下降有一定容忍的场合。

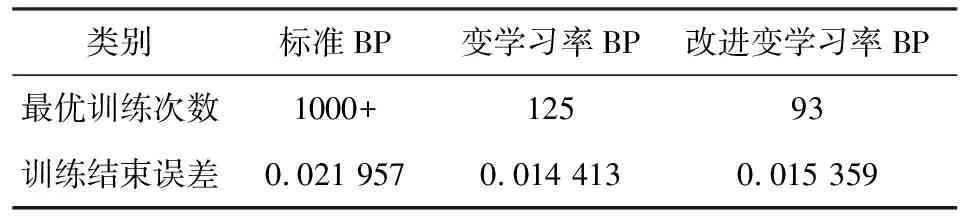
表2 三种算法的训练结果

4 结 语

提出一种运用于风电机组故障检测的改进变学习率BP神经网络，通过计算最近两次训练的误差的差值来动态调节BP神经网络的训练步长，以达到缩短训练时间、提升训练误差的收敛速度的目的。

通过对改进变学习率BP神经网络与变学习率BP神经网络和标准BP神经网络的误差随训练循环次数变化情况的曲线进行对比，并运用实际的风电机组运行数据对改进变学习率BP神经网络的收敛性能进行验证，一方面证明了改进变学习率算法相比变学习率算法可以缩短训练时间，另一方面证明了改进变学习率BP神经网络对于风电机组故障检测的适用性。