基于PSO-BP算法的光伏发电功率预测

2021-06-18房俊龙

黑龙江电力 2021年2期

崔响，房俊龙，曲乐

(1.东北农业大学电气与信息学院，哈尔滨 150031；2.国网黑龙江省电力有限公司哈尔滨供电公司，哈尔滨，150090)

0 引言

在目前现代化生产中，人类所利用的主要能源是煤、石油、天然气等不可再生能源。但长期使用这些能源不仅会造成能源枯竭，同时，这些能源在燃烧时释放的气体，也是全球环境变暖、温室效应加重的主要诱因[1]。近年来，人们逐渐认识到，解决能源问题的最终方案是采用可再生能源取代传统不可再生能源[2]。而光伏发电以其具有无污染，安全可靠等优点成为世界各国关注的目标。并且光伏发电具有极低的碳排放量，尤其是在低碳经济发展的当下，光伏发电成为最具有潜力的电力能源之一[3-4]。

目前对光伏发电的预测有两种分类：一是建立太阳辐照-光伏出力的物理模型，借此对光伏发电出力进行预测[5-8],这种方法可以在没有任何历史数据的情况下直接对光伏发电功率进行预测，但需要大量的光伏电站信息，以及诸多光电转换参数来建立更加精确的物理模型，最后结合光电转换效率等信息得到预测值;二是基于大数据应用智能算法进行预测[9-12]，这种方法无需光伏电站以及光电转化的信息，只需要对历史的输出功率、天气、辐照等数据进行统计和整理，使用这些数据对算法模型进行训练来建立输入-输出的非线性关系，对待测日的功率进行拟合，最终得到所需的输出功率。

目前，通过大数据应用智能算法进行预测的研究越来越多，该文所讨论的是采用粒子群优化的BP神经网络算法(下称PSO-BP算法)对光伏出力的预测。

1 光伏发电原理

光伏发电是指利用半导体界面的光生伏特效应将光能转化为电能的一种技术。当光子照射到金属上时，它的能量可以被金属中某个电子全部吸收。如果电子因此获得的能量足够大就能从金属表面逸散出来，成为光电子。硅原子中有4个外层电子，如果在其中掺入了具有5个外层电子的原子(如磷原子)，就成为N型半导体；若掺入了具有3个外层电子的原子(如硼原子)，则形成P型半导体。P型与N型结合在一起时，表面会形成电势差，成为光伏电池。当太阳光照射到P-N结之后，电子由N极区向P极区移动，形成了电流。

光伏发电的影响因素有很多，文献[13]给出了单位面积光伏阵列的输出功率表达式：

Ps=ηSI[100.005(t0+25)]

式中：η为光电转化效率;S为光伏阵列面积;I为辐射强度;t0为大气温度。

对于同一光伏电站，光电转化效率和光伏阵列面积是固定不变的，所以辐射强度与大气温度是实际影响光伏发电输出功率的主要因素。太阳辐射强度就是指太阳在垂直照射的情况下在单位时间内，1 cm2的面积上所得到的辐射能量。在光电转化效率一定的情况下，与光伏发电输出功率呈正相关。在大气温度单独作用下，与光伏发电输出功率呈负相关关系。大量实验统计表明，温度上升1 ℃，晶体硅太阳电池的最大输出功率下降0.04%，开路电压下降0.04%，短路电流上升0.04%。

在实际的光伏发电系统中，光伏发电的输出功率是辐射强度与大气温度共同作用的结果。这两个因素可作为判断相似日的主要参数。同时，还有其他的一些因素也会影响光伏发电的功率，如风力、光伏阵列的安装角度等。

2 PSO-BP算法预测的实现方式

2.1 PSO-BP算法

如引言所述，随着对光伏发电功率预测的研究，越来越多的学者开始或已经使用人工智能算法对光伏发电功率进行预测。常见的算法，诸如BP神经网络、粒子群算法、灰度算法、支持向量机等都已有人将其应用于该领域并取得了较为出色的成果[14]。

粒子群算法(PSO算法)本身就是一种收敛速度快、全局搜索能力强、鲁棒性强的算法。使用PSO算法对BP神经网络进行优化可以有效解决BP神经网络的缺点，改进算法精度以及收敛时间。PSO算法目前已经广泛应用于包括风电在内的诸多领域之中，但在光伏发电功率的预测方面却鲜有研究。

在PSO-BP算法中，依旧采用BP神经网络的结构，即输入层-隐含层-输出层的结构方式，但不使用梯度下降的方式进行训练，而是将隐含层中各个权值/阈值作为PSO算法的粒子，神经元个数作为PSO算法的种群数。在算法进行训练学习时，首先将随机生成的粒子初始值赋予BP网络中对应神经元的阈值与权值并得到训练结果，计算与期望值之间的误差E。自然，由于粒子初始值为随机值，会产生极大误差。随后将该组权值/阈值作为粒子，使用PSO算法对粒子的位置和速度进行迭代，表达式如下：

V1=W·V0+c1·rand·(pBest-X0)+

c2·rand·(gBest-X0)

X1=X0+V1

式中：V1是待更新的速度；V0是当前速度；W是惯性权重；c1、c2是学习因数；pBest与gBest分别为个体最优与群体最优值；X1为待更新位置；X0为当前位置；rand为随机数，区间为(-1,1)。

BSO-BP算法流程框图如图1所示。

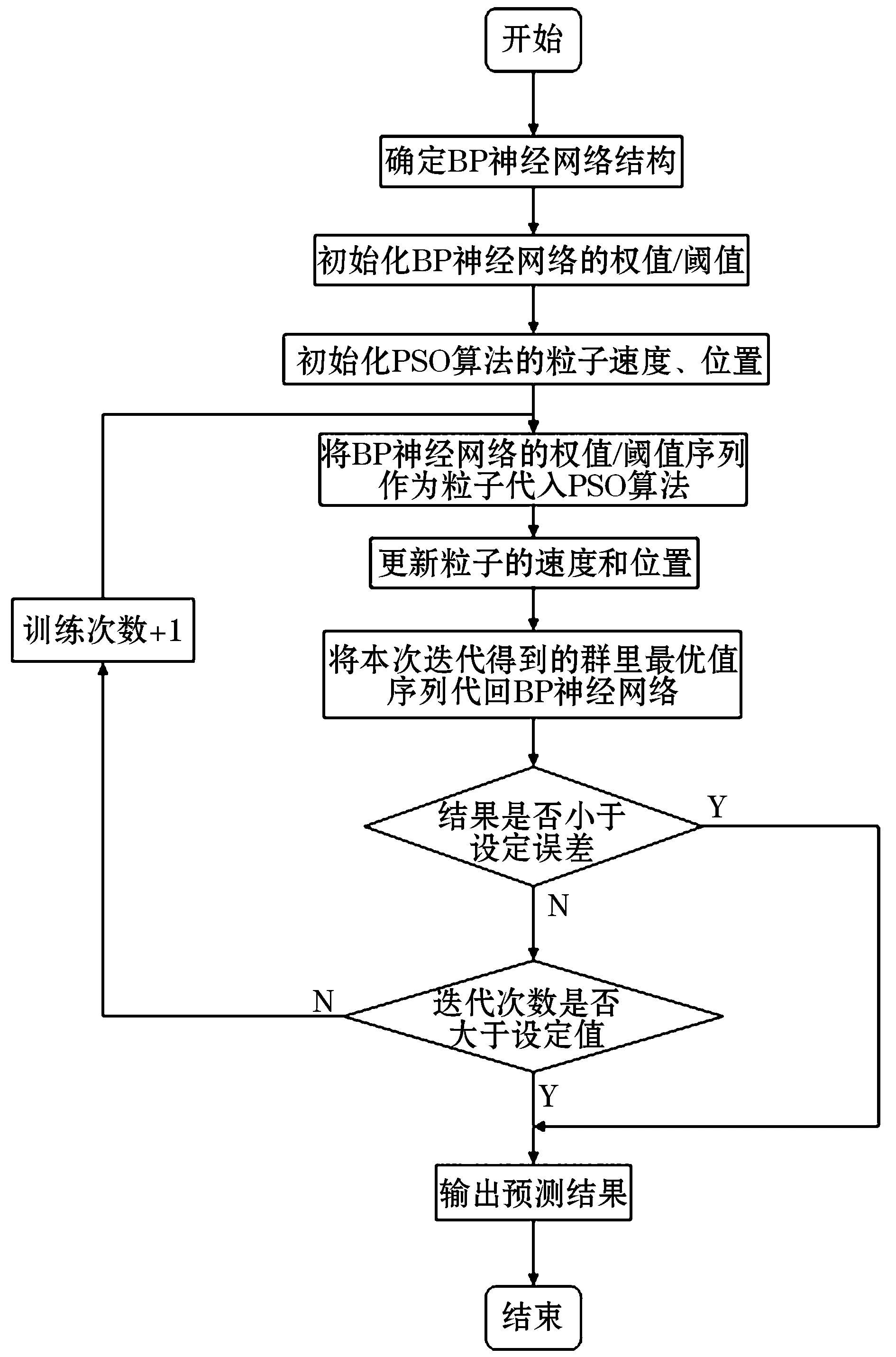
图1 PSO-BP流程框图

PSO算法进行迭代寻优之后，将迭代所得到的粒子值再次赋予BP网络中对应神经元的阈值与权值并进行训练得到训练一次之后的结果，再次计算误差E。如此反复直至误差E缩小到设定误差为止。

2.2 PSO-BP算法对光伏发电功率预测的实现

应用PSO-BP算法对光伏发电功率进行预测，需要有历史数据作为支持来挑选相似日作为基准。选择单日最高温度、单日最低温度、单日太阳辐射强度，作为挑选相似日的参考量。通过计算历史数据与待测日的欧氏距离来确定相似日，欧式距离为

式中：tmax、tmin是历史数据中各单日最高、最低温度；t0max、t0min是待测日的最高、最低温度；Q是历史数据中各单日辐射强度；Q0是待测日辐射强度。

基于上述方式，可以挑选出与待测日的天气环境相似的数个单日，作为相似日，并获得该日8-17时每小时节点的对应输出功率。将这10个功率与当天的最高、最低温度、辐射强度作为一组数据，反复此过程，即可获得数组数据。对数据进行随机分组并代入算法中进行训练，即可得出最终用于预测的模型。

3 基于PSO-BP算法的光伏发电功率预测

3.1 原始数据处理

由于输入数据的量级以及单位各有不同，直接将原始数据输入网络会使得微小的数据变动引起较大的结果变化，对结果有较大的影响。为了避免这类误差的产生，应对所有数据进行归一化处理。归一化后所有数据会被归为[-1,1]区间，表达式如下：

式中：y为归一化的结果；x为原始数据；xmax和xmin分别为该组数据中的最大值与最小值；ymax和ymin分别为归一化的上下限。

3.2 神经网络节点和神经元个数的确定

选用待测日的辐射强度、最高温度、最低温度，以及基准日8-17时的光伏发电功率数据，共13个数据作为输入，即输入节点为13个。输出节点数为待测日8-17时的光伏发电功率，即10个。

神经元个数确定方式目前尚无统一定论。较为主流的观点是使用Kolmogorov定理大致确定神经元个数，之后通过try-error-try，即反复尝试的方法确定最优神经元个数。

Kolmogorov定理公式如下：

或

n1=log2(n2)

式中：n2为理想中的神经元个数；n1为输入层节点个数；m为输出层节点个数；a为[1,10]区间内的任意数。

通过上述方式，确定神经元个数为15个。

3.3 PSO-BP神经网络的建立

如2.2节所述方法，在该季度的历史数据库中挑选与待测日欧氏距离最小的10个值所对应的日期作为相似日。在两两随机分组后，使用Matlab工具箱的指令，建立5组13-15-10的BP神经网络并应用2.1节中的PSO算法进行迭代寻优，将最终群体最优值回代入网络，以此实现对网络权值/阈值的训练。分别得到5组网络预测结果之后，计算每组的相对误差，取误差最小的模型作为最终算法模型。

4 算例分析

采用美国俄勒冈大学光伏站的公开数据[15]，根据第3节的内容建立预测模型，采用ASHLAND 2016年4月光伏数据作为数据样本，使用Matlab进行仿真。在进行误差对比之后选择第二组神经网络作为最终预测模型，并应用该模型对4月16日的光伏发电功率进行预测，其预测的结果如图2所示。

图2 PSO-BP算法的预测曲线

由图2可以得出，该算法整体拟合程度较好。在上午和下午的3个时点的拟合精度较高，而在中午和日落前拟合精度略差。

误差修正曲线如图3所示。可以看出，在100次之前误差下降率非常高，说明该算法可以迅速获得拟合区间；在300次迭代之后，误差已经趋于稳定。

图3 误差修正曲线

误差分析图如图4所示。可以得出，总体相对误差约为4.4%。而BP神经网络的预测精度在8%～10%之间。由此可见，使用PSO-BP算法进行预测可以大幅提高整体预测精度。分析后发现，误差较大的主要时间为日落时，分析认为在日落时存在太阳斜射电池板、云层遮挡、大气折射等因素导致整体出力波动较大。并且，在原始数据中17时的功率波动最大可达100%，这也是导致最终预测结果差距较大的主要原因。