考虑库存成本下的多目标供应商选择问题研究

何波波 李建婷

(兰州交通大学 交通运输学院 兰州 730070)

引言

随着经济全球化、顾客需求个性化和产品多样化时代的到来，供应链管理过程不仅是资金流、信息流的流动，更多的是产品的增值过程。供应商的交付水平以及融资运营都会影响到下游制造商[1]。合理的供应商选择能够减少企业的成本、增加企业的利润，同时也能提高顾客的满意度，这使得供应商选择问题成为近些年国内外学者研究的热点[2]。

Ventura等[3]在研究两阶段中的供应商选择与订单数量分配的问题中，建立两种混合整数非线性规划模型。Alegoz等[4]提出了一种基于模糊TOPSIS，梯形模糊层次分析法和目标规划的混合方法。王一雷等[5]将供应商的碳排放加入到选择标准中，以AHP和GP相结合的方法进行了研究，且通过实例验证了方法的有效性。Svoboda等[6-7]考虑库存风险，研究了厌恶风险的供应商和过于自信的制造商的最优决策和策略偏好，为库存模型的提供了研究方向。雷绍雍等[8]在综合考虑装备采购中，构建多目标约束的指派模型，并运用遗传算法进行求解。Jadidi等[9-13]研究在供应商能力有限的情况下，考虑数量折扣，以及多产品供应的数量分配问题，设计启发式算法进行求解验证，其中文献[13]设计蛙跳算法求解，取得了很好的效果。Che、杨桂芝等[14-15]在求解供应商选择问题时运用改进的遗传算法NSGA-II，求得多目标规划的Poreto解，并与加权求和法做了对比，发现NSGA-II算法在时间和解的效果上明显更优。亓尧等[16]就供应商选择问题建立基于悲观值和乐观值的机会约束规划，转化为等价方法进行求解。

综上可知，现有文献多是研究确定环境下单产品供应商选择问题，对不确定环境下的多产品供应商的选择问题研究较少；同时，供应商选择问题大多并未将库存成本考虑在内，即使考虑在内，也是以一个常数表示，这与现实情况不符；另外，极少有文献对多产品供应商选择问题研究它的批量限制和数量折扣等情况，对供应商的服务水平指标选取单一。基于此，本文在现有文献的基础上，考虑到市场对产品的随机需求，给出了价格、质量、交货能力、采购提前期、售后服务水平、供应商产品的配额柔性等作为供应商选择问题的评价指标。同时，也考虑到制造商的需求量、供应商的供应能力以及由于产品缺货风险而造成的损失问题，将库存成本以分段函数表示，建立了多产品、有折扣、无缺货情况下的供应商选择问题的机会约束规划模型。以总成本最小、次品数量最小和延迟交货数量最小为目标，将随机模拟、神经网络、NSGA-II算法相结合设计了混合元启发式算法对该问题进行求解验证。

1 多产品供应商选择问题的多目标规划

问题描述：在整个供应商选择的过程中，单一地选择一家供应商不足以应对瞬息万变的市场，采购商需要从多个供应商处采购产品。这就要求供应商也能供应多种产品，才能不被市场淘汰。供应商和采购商两者相互配合满足广大居民的需要。为了最大化各自的利润，以成本、次品数和延迟数三准则为目标函数，其余各目标为约束条件建立供应商选择问题的多目标规划模型。由于多目标之间是相互冲突的，不能同时满足目标要求，可将其转化为不确定环境下的随机机会约束规划。在不能完全满足约束的情况下，假定目标和约束条件是在一定的置信水平上成立，这样求出的决策方案更符合实际。

1.1 模型假设

假设1: 采购商可从每个供应商处采购多种商品，且商品间相互独立。

假设2：当采购数量达到一定范围时考虑数量折扣，且采购的所有同种物品价格统一。

假设3：任何供应商的商品均不允许缺货。

假设4：运输成本由供应商承担。

假设5：物品前置期为常数。

假设6：供应商必须按时按质地完成制造商的产品，否则会受到相应的惩罚；

假设7：供应商最大化自己利润，对小批量订单也不放弃，但是限制最小的总批量。

1.2 多目标规划模型

1)目标函数

模型Ⅰ

最小化采购费用：最小化购货成本包括产品成本、订货成本、运输成本、存储成本以及处罚成本等。由于运输成本由供应商承担，故不考虑运输成本。考虑到供应商的折扣价格，采购商可能采购更多的物品，从而增加没必要的库存，产生额外的库存费用。假设此模型未考虑存储成本外的其他运作成本，仅产生存储费用M。另外，考虑到现实因素各供应商存在未按时按质交货的情况，采购商对此设置了相应的处罚，但是比起产品缺货与质量问题造成的损失，处罚成本显得少之又少，故可加到总成本。

(1)

i:供应商序号，i=1,2,…,I；

j:供应产品种类的序号，j=1,2,…,J；

t：第t个阶段的折扣，t=1,2,…,T;

xij：向供应商i处订购产品j的数量(决策变量)；

pij:无折扣时供应商i供应产品j的单价(包括运输成本)；

eij：供应商i对供应产品j未按时按质地交货所产生的单位处罚成本；

qij：供应商i交付不合格产品j的百分比；

dij：供应商i逾期交付产品j的百分比；

rijt：从供应商i处订购产品j的数量达到相应要求时，第t个阶段的折扣；

Dj:产品j的计划总需求量(随机变量)；

Oi：采购商付给供应商i的订货费；

(2)

令zi=h(xij)，当zi=1时，表示供应商i至少供应一种产品；否则，zi=0，表示供应商i不供应任何产品。

M：采购商对所有采购物资的库存费用(这里假设任意产品都是同样的价格，库存费用只与存储数量有关)。

1923年7月，蔡元培偕夫人周养浩(1892—1975)和子女再度赴欧洲学习考察，先居住于比利时布鲁塞尔，次年1月移居法国。1924年8月，蔡元培自法国赴荷兰、瑞典参加一个关于哥伦布未发现新大陆之前美国民族问题的国际民族学会议，巧遇但采尔。此时，但采尔已从莱比锡大学博士毕业，在汉堡大学做教授。

(3)

其中，A,a,b为常数，A为存储的起步价格，当存储数量小于等于a时，使用统一价格A元，当存储数量超过a时，每多一件产品，费用增加b元，存储数量无上限。

最小化采购产品的次品数量：任何采购商在决定采购方案之前都会在多家供应商中进行比较，结合多种评价指标以及该供应商所设置的某种产品的次品比例，选取产品质量最优的供应商作为最佳选择。

(4)

最小化采购产品的延迟交货数量：由于供应商的多样性，不同供应商有不同的信誉。采购商根据自己设置的延迟交货比例以及各供应商以往所供产品的评价等级等多种指标体系，选择信誉较高、延迟数量最少的供应商供应某种产品以达到采购商的目的。

(5)

2)约束条件

xij≤Uij

(6)

Uij：供应商i可提供产品j的上限。

(6)式表示供应能力约束。供应能力是供应商选择问题的一个重要指标，任何采购商订购产品皆不能超过各供应商的供应能力。

(7)

(7)式需求约束。由于此问题是建立在无缺货的基础之上，从各个供应商处采购的各种产品总量要超过计划需求量Dj。

(8)

ui：供应商i对采购商要求采购的总最小量。

(8)式最小采购约束。从供应商的角度考虑，为了最大化利润，供应商i要求采购商在该处的采购总量要大于等于预先设定的数额，才可安排人力物力供应该产品。

(9)

Sj：采购方对产品j要求的最低服务水平。

(9)式服务水平约束。由于企业间的竞争，任何采购商都会考虑各供应商的售后服务水平，即对该产品由于多种原因造成的损失后，所采取补救措施的有效性。以此来判断是否达到采购商规定的计划订购量与服务水平的乘积要求。

(10)

fij：供应商i对产品j的配额柔性，以调查专家打分的历史数据得出适应外部环境和内部环境的改变而做出调节的能力；

Fj：要求供应商对产品j供应配额柔性的下限。

(10)供应商的配额柔性约束。供应商的配额柔性指的是在企业活动生产中，供应商处理环境变化或者其他不确定变化的能力，包括适应性能力，创新性能力以及其他能力。它们的综合评价应大于等于采购商规定的一定数量产品所具有的配额柔性。

(11)

vij：供应商i对产品j所得的评价值；

Vj：采购商要求供应商对产品j要求的评价值下限。

(11)式供应商评价值约束。采购商在采购完该供应商产品后，经过一系列过程会分销出去，进而得到不同顾客的反馈。为了提高供应商产品的质量，采购商会公示各供应商的信用度、准时性、产品合格率、付款合理性等多种指标，综合得到供应商的评价值。

1.3 随机机会约束规划模型

模型Ⅱ

(12)

s.t.

xij≤Uij

(13)

(14)

(15)

(16)

(17)

(18)

(19)

在上述所有目标函数和约束条件中，i=1,2,…,I；j=1,2,…,J，上式中Pr{•}，表示{•}此事件以一定的置信水平成立。α,β为决策者为限定机会约束成立而预先设定的置信水平。

2 混合多目标遗传算法设计

由于本文求解模型是多目标优化，与单目标优化不同。某些目标的优化可能会导致其他目标的劣化。所以，对于多目标优化问题一般难以求得问题的最优解，而是求得问题的最优解集，也就是最接近目标的满意解。一般情况下，用非劣解集或者Pareto解集表示，即Pareto前沿。基于此文章利用随机模拟技术为成本函数产生输入输出数据，并训练一个向前的神经元网络来逼近不确定函数，最后与NSGA-II算法相结合产生混合多目标遗传算法。NSGA-II算法是Deb为了克服NSGA算法的缺点而提出的一种改进算法—带精英策略的非支配排序遗传算法。

2.1 NSGA-II算法

2.1.1 NSGA-II算法优点

1)提出快速非支配排序算法，降低了算法的复杂性。假设种群规模为N，目标函数个数为m，则遍历整个种群，由之前的复杂度o(mN3)降低为o(mN2)。

2)引入精英策略，将父代种群与子代种群合并，共同竞争产生下一代，扩大了采样空间，有利于优良个体被继续选择，并对种群进行分层，提高种群的整体水平。

3)提出拥挤度和拥挤度比较算子，弥补需要制定共享半径的缺点，并能在同级种群中选出更好的个体，并将Pareto域中的个体扩展到整个Pareto域，保证了种群的多样性。

2.1.2 主要思想

1)通过随机产生规模为N的初始种群P0，依据NSGA算法进行非支配排序，指定每个个体的层次值。随后进行遗传算法的选择，交叉与变异操作，产生第一代子代种群Q0。

2)从第二代开始将父代种群Pt与子代种群Qt合并后的种群Rt(规模为2N)，进行快速非支配排序，同时对同层的非支配个体进行拥挤度计算和排序，根据非支配序值和拥挤度选择合适的个体组成新的父代种群。

快速非支配排序指：先找出群体中的非支配解集，记为F1,将其中所有个体的非支配序赋值为rank=1，并从整个群体中将F1中的个体移去，在剩余的群体里找到非支配解集，记为F2，相应地rank=2。以此类推，直到整个群体被分层。

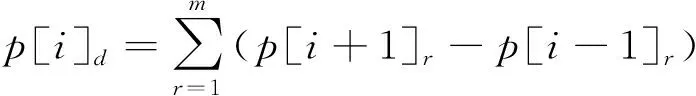
3)通过遗传算法的选择、交叉和变异产生新的子种群。

2.1.3 算法设计

1)编码设计。标准遗传算法采用二进制编码，但它具有一定的缺点。文中使用浮点数编码，二维数组表示。二维数组的每个值表示决策变量的值(即基因值)，此方法具有计算方便、操作效率高等特点。假设向量Xk为一条染色体，结构设计如图1，其中0≤i<3，i为供应商的数量，j为产品种类。其中xij表示供应商i供应产品j的数量。例如：6种产品，有3个供应商可供选择，如下所示：

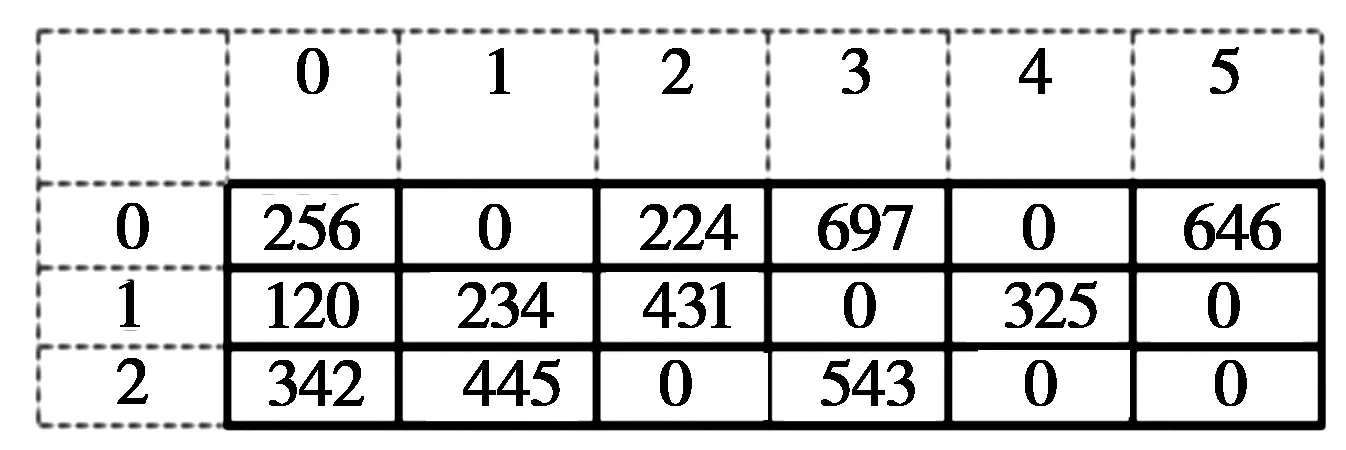
图1 染色体结构设计

即：供应商1提供产品1,3,4,6，数量分别为256、244、697、646；供应商2提供产品1,2,3,5，数量分别为120、234、431、325；供应商3提供产品1、2、4，数量分别为342、445、543。

2)初始解的产生。首先在各供应商供应能力允许的范围内随机产生满足约束1的解(即为染色体)，将其保存，判断这些染色体是否满足约束2，如果满足继续保存；如果不满足，直接舍弃；判断约束2中保存的染色体是否满足约束3，以此类推，直到找到满足约束6的染色体并将其保存。重复以上步骤，直到最终保存下来的满足约束6的染色体个数为po_size(种群规模)时停止，以这种方法产生的初始种群能够有效避免解的无效性。

3)评价函数。适应度值的好坏是评价个体能否存活更久的关键指标。由于多目标优化问题的目标函数往往是相互冲突的，无法求得最优的一个解，这里通过非支配排序原理对种群进行分层得到不同个体的序值(作为适应值)，从序值rank=1的个体集开始。适应值越小，个体越优。

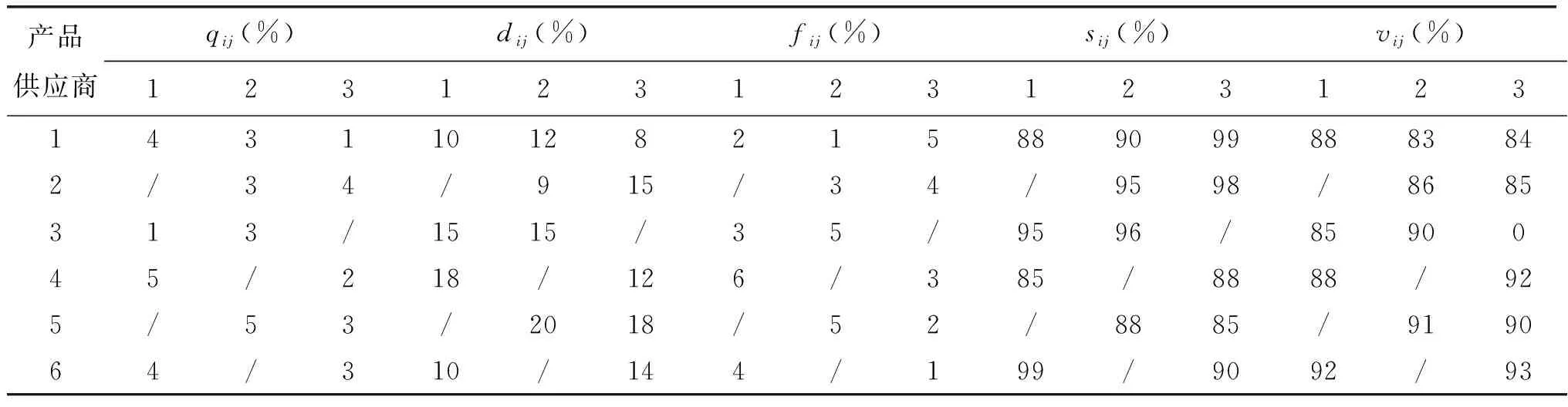
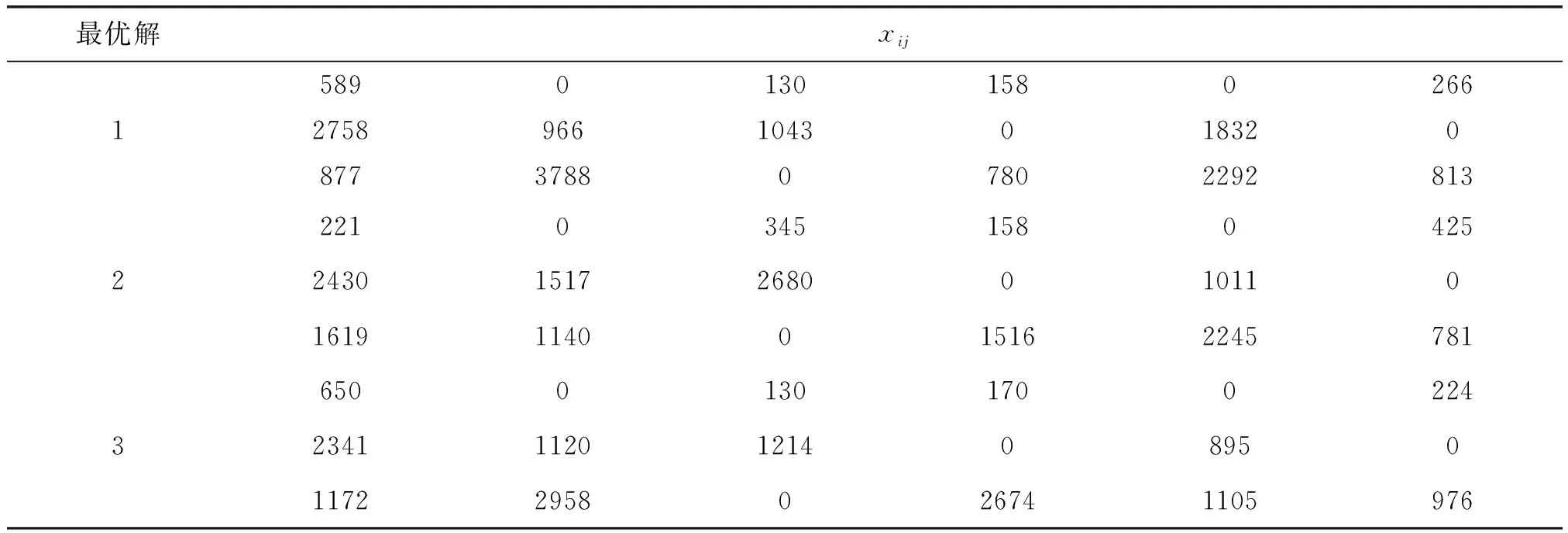
4)选择算子。选择过程采用最佳个体保存和锦标赛结合的方法。随机地从po_size中选取k个个体(k

5)交叉算子。采用单点交叉，定义一个交叉概率pc,则每一次进化的种群中平均有pc·po_size个个体进行交操作。将个体1与个体2交叉，个体3与个体4交叉，个体i与个体i+1作为父代交叉。此方法保证将相异的优良的个体经过交叉后要么变得更优，要么直接遗传。加快寻优的速度。首先随机产生0到1 的小数cross，重复进行po_size次，每进行一次都判断cross与pc的大小。

如果cross≤pc，则在{0,1,2,…,i}(0≤i

如果cross>pc，则将原来两条染色体直接遗传至下一代。

图2 染色体交叉

6)变异算子。定义pm为变异概率，表示每次进化中有pm·pop_size个染色体发生变异，即进行变异操作。这样做的目的是为了增加个体选择的范围、扩大种群的多样性。前期采用均匀单点变异的方法，后期采用提高局部搜索的高斯变异。先随机产生0到1 的均匀小数variation，重复进行po_size次，每进行一次都判断variation与pm的大小。

如果variation≤pm，则首先在{0,1,2,…,i}(0≤i

图3 染色体变异

7)停止准则。采用固定代数的方法，判断是否达到预先设定的代数，若是则终止迭代，输出结果，否则继续。

2.2 算法流程图

3 实例分析

假设某采购商需要采购6种产品，可供选择的供应商有3个。每个供应商都可以提供相应范围的折扣价格，且至少可以提供四种产品。采购商规定的惩罚价格为产品价格的两倍。折扣阶段T=2。在各约束条件下，运用VS2013进行了仿真计算。所需的数据如下所示。表1为供应商的供应量、采购商的需求量和订货费；表2为供应商供应能力的各指标；表3为各产品的单价；表4为采购商对供应商指标的参数要求。

表1 产品供需量及订货费

表2 供应商供应能力指标

表3 各产品单价(元)

表4 对供应商各能力的参数要求

各供应商给出的数量范围价格折扣：

3.1 参数设置

结合上述算法，设置相应的参数如下：100次循环迭代；50个种群规模，循环5000次；1000个训练样本；交叉概率为0.8；变异概率为0.05；需求量Dj服从正态分布N(μ,σ2)，μ、σ分别从区间[2000,6000]和[10,15]中随机产生。置信水平(α,β)=(0.85,0.9)；存储的起步价格A=2000元；存储数量的分界值a=6000件；超过数量a的每件产品价格b=0.2元。

3.2 结果分析

将数据代入求解算得Pareto序值为1的解有10个，这里取其中三个做对比分析，其他解相似，如表5、6所示。

表5 Pareto最优解

表6 目标函数值

表5中的每个最优解都对应表6的一种采购方案，可以看出，供应商2和3由于其自身的优势，获得较大的市场配额。但是供应商1，由于各项需求的约束、自身服务能力的不足及以竞争的劣势，所获得的市场配额相对较少。 总的来说，供应商2和3在市场中供应产品相对稳定，其信誉度较高。采购商采购产品时，可根据实际情况做出决策，给予供应商1更少的配额或者不给予任何配额。如果确需选择供应商1来提供产品，可指定订购供应商1的第一种产品。

3.3 结果对比(选方案1)

表7 算法结果对比

从表7中对比可知，NSGA-II算法较其他智能算法能明显提高运算效率，节省运算时间,并能取得最优解集。若多目标遗传算法适应度采用之前的加权求和方法，加入人为的主观因素，虽然能求得最优解，但是权重不同，计算结果也不尽相同。若权重选择不合理也可能获得解的实际意义不大。在以后的计算中，可多应用NSGA-II算法解决NP-难问题，可提高运算效率，快速寻得更优解。

4 结语与期望

文章研究了多产品，有折扣情况下的供应商选择问题，这一类问题在供应链中具有重要的意义。文中以最小化成本、次品数量和延迟数量为目标，建立多目标规划模型，进而转为机会约束规划。通过设计智能算法求得最优解。本文的创新点在于将多目标进化算法NSGA-II、随机模拟、神经网络相互结合求解问题的Pareto解。此方法在仿真过程中求解效率更高，也避免了加入权重这些人为的干扰因素。这样获得的解更有优说服力，方便决策者选择最佳方案。其次，文中将库存成本设计为一个分段函数，以库存数量和为自变量，库存费用为因变量。当库存数量在一定范围时，设置为一个统一价格，之后随着数量的增多，库存费用以单价方式倍增，这样做更切合实际。在今后的研究中可从以下方面进行研究：

第一，该模型是在前面诸多假设的基础上，如任何商品均不允许缺货、产品间相互独立、未考虑其他运作成本等，这与现实中的特殊情况不符，可进一步考虑问题，建立更完善的模型。第二，NSGA-II算法虽然保证了进化解的公正性，但是选择途中也易产生退化解，后续研究可引入博弈论来避免这种现象的发生。