基于相干态指针实现光机械系统中的弱测量放大
2021-06-18李刚
李 刚
(延安大学 物理与电子信息学院,陕西 延安 716000)
在1988年,弱测量理论由Aharonov等人提出[1],通常被称之为弱值放大机制(Weak value amplification regime,i.e.,WVA regime)。之后,弱测量的概念引起了一些争议,但很快它的物理含义就被澄清了[2]。到现在为止,弱测量已成为最有前途的精密测量工具之一,它已应用于各个研究领域,包括解决量子力学中的基础问题[3,4]和解释一些违反直觉的量子悖论[5]。在弱测量中,指针弱耦合到被测量的系统。与投影测量对比,如果指针的初始波函数的宽度很大,则在弱测量中指针的输出信号(即指针观测量的值)会远远超出系统观察量的特征值的范围。这个结论归因于指针的量子态叠加(量子干涉效应):当被测量的系统发生接近正交的后选择后,指针的两个或多个稍微不同的平移高斯态的叠加[1,6]可以给出系统观察量的值超出其特征值的范围。最近发现,弱测量可以帮助测量较小的物理量[7]或对较小的物理参数进行灵敏地估计[8,9],然而传统技术很难直接检测到它们,大多数弱测量方案都可以通过经典波动力学来解释[8-10]。此外,更多有关弱测量领域的评论可以参考文献[11,12]。
尽管弱测量有许多应用,但其在光机械系统中的应用很少被研究[13,14]。光学机械系统由一个光学腔和一个可移动镜组成,腔中的光子会在反射镜上产生辐射压力,并使镜子产生位移。在光机械弱耦合条件下,当腔中只有一个光子时,很难检测到镜子的位移,那是因为由一个光子引起的镜子位移远小于镜面波包的宽度。最近,标准弱测量方案[1]可以通过福克态视角来理解[6]。考虑镜子的初始态为基态,我们发现使用弱测量可以放大由一个光子引起的镜子的位移[15],这个结果是通过保留克尔相位获得结果[16]。在有关标准弱测量的大多数讨论中,都将指针的初始化为基态,而弱测量的一个重要特征是,在被测量的系统上进行接近正交的后选择后,几个指针态的叠加可以产生放大效果[2]。这些指针态之间的相对相位起着关键作用,可以通过后选择进行调整。正如人们所知,相干态被视为经典态,自然地我们想要知道,当指针最初被制备在相干态时,在弱测量中是否存在一些新量子特征。
本文考虑结合弱测量的光机械系统方案。当镜子处于相干态时,我们发现在正交选择下能够放大镜子的位移,其最大放大值可以在时间附近发生,这对于品质因子差的光机械腔非常重要,即光腔的衰减率非常大,因此该方案在当前实验条件下是可行的。这些结果是被两个镜子态之间的相对相位引起的,然而相对相位起源于量子力学的非对易性[17]。因此,它对于弱测量来说是一种新的有关放大的物理机制。
1 光机械系统的弱测量放大
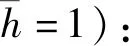
H=ω0(aa+bb)+ωmcc-gaa(c+c),
(1)


一个光子进入第一个分束器,然后进入光机械腔A和常规腔B。光子微弱地撞击小镜子。在第二个分束器之后,在暗口检测到光子,即后选择发生,否则,后选择失败。
假设一个光子输入到干涉仪中,则第一个分束器之后的光子状态变为
(2)
而镜子初态被制备在相干态|α〉[20],α=|α|eiθ,其中|α|和θ都是实数,分别称之为相干态的振幅和相位。与处于相干态的镜子微弱相互作用之后,整个系统的状态变为
|Ψom(t)〉=(|1〉A|0〉B|Ψ(ξ,φ,t)〉m+
(3)
以及
|Ψ(ξ,φ,t)〉=eiφ(t)D(ξ(t))|φ(t)〉m,
(4)
其中φ(t)=k2(ωmt-sinωmt),
D(ξ(t))=exp[ξ(t)c-ξ*(t)c]是一个平移算符,ξ(t)=k(1-e-iωmt),k=g/ωm和φ(t)=αe-iωmt。
当在暗口检测到光子时,表明后选择发生,即对单光子系统进行投影测量[15],则单光子的后选择状态为
(5)
其正交于|Ψi〉。然后,镜子的最终状态变为
|Ψos(t)〉=(|Ψ(ξ,φ,t)〉m-|φ(t)〉m)/2。
(6)
为了简化分析,可以平移等式(6)的态到相空间原点,定义|χos(t)〉=D(φ(t))|Ψos(t)〉,于是可以获得
|χos(t)〉=(exp[iφ(t)+iφ(α,t)]|ξ(t)〉m-
|0〉m)/2,
(7)
其中这个相eiφ(t)+iφ(α,t)是相干态|ξ(t)〉m和基态|0〉m之间的相对相位,其中
φ(α,t)=-i[(ξ(t)φ*(t)-ξ*(t)φ(t))],
它是通过平移算子的性质
D(α)D(β)=exp[αβ*-α*β]D(β)D(α)
(8)
获得的,即量子力学的非对易性。在文献[15]中,正交选择发生后两个镜子态之间的相对相位是由克尔相位引起的,并可以导致弱测量放大效应。
下面将给出如何通过该相对相位来产生镜子微弱位移的放大。
2 通过相干态指针放大镜子位置变量q
在弱测量中,镜子的指针变量q的平均位移为

(9)
通过等式(6),并且代它进入等式(9),可以获得
〈q(t)〉=σ[ξ(t)+ξ*(t)-e-|ξ(t))|2/2(eiφ(t)+iφ(α,t)
ξ(t)+e-(iφ(t)+iφ(α,t))ξ*(t))]/
[2-e-|ξ(t))|2/2(eiφ(t)+iφ(α,t)+e-(iφ(t)+iφ(α,t)))],
(10)
其中相位eiφ(α,t)是从量子力学非对易性中产生的相对相位。
对于不同的相干态|α=|α|eiθ〉,在图2中镜子的平均位移〈q(t)〉/σ显示为时间ωmt的函数,其中k=0.005。从图2清楚可见,在ωmt=0附近发生的放大可以达到单光子强耦合极限(零点涨落程度)〈q〉=σ或-σ[21]。这个结果对于品质因子差的光机械腔非常重要,因为光腔的衰减率非常大,使光子可能在很短的时间内从腔中泄漏出来。而且,对于某些相干态,在ωmt=0附近放大的时间间隔是较宽的,因此更易于实验检测,这与文献[15]中的ωmt=0附近放大的时间间隔形成鲜明对比,而在文献[15]中放大的时间间隔是非常狭窄的。注意,由一个光子在腔中引起的镜子的最大位移(见图2(a))为4kσ,而在弱测量下,此处获得的镜子的最大位移可以达到σ或-σ,因此放大因子可以为Q=±1/4k。例如,当k=0.005时,Q=±50,即相当50个光子撞击在镜子上引起镜子位移。
接下来,将给出如何通过该相对相位来产生镜子微弱位移的放大。

(a)不同振幅|α|和不同相位θ的镜子的平均位移〈q(t)〉/σ,其中k=0.005(|α|=1/2和θ=0(实线),|α|=1和θ=π/3(点划线),|α|=2和θ=5π/12(虚线),|α|=4和θ=π/2(点线));(b)不同振幅|α|和不同相位θ的镜子的平均位移〈q(t)〉/σ,其中k=0.005(|α|=1/2和θ=π(实线),|α|=1和θ=4π/3(点划线),|α|=2和17π/12(虚线),|α|=4和θ=3π/2(点线))。
3 对于放大效应进行时间的泰勒展开
为了探讨在ωm(t)=0附近发生的放大效应,对于等式(7),可以在时间0处进行泰勒展开直到第一阶。假设ωmt≪1和k≪1,则
|χos(t)〉≈[ikωmt|1〉m+i2k|α|((ωmt)2sinθ/2+
ωmtcosθ)|0〉m]/2,
(11)
它是|0〉m和|1〉m的叠加态,而|0〉m的幅度是归因于量子力学的非对易性引起的相对相位eiφ(α,t)。因此,|0〉m和|1〉m的叠加是获得放大的关键。在等式(11)中,当
kωmt=2k|α|((ωmt)2sinθ/2+ωmtcosθ)
(12)
时,镜子的位移可以达到最大值σ,当
kωm(t)=-2k|α|((ωmt)2sinθ/2+ωmtcosθ)
(13)
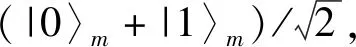
4 基于耗散的位置变量q的放大
考虑到耗散,机械系统的主方程为[19,22]
dρ(t)/dt=-i[H,ρ(t)]+γm[2cρ(t)c-ccρ(t)
-ρ(t)cc]/2,
(14)
其中γm=是阻尼常数。通过等式(14),给出机械系统的耗散演化解析解或者数值解,再与无耗散的等式(6)进行对比,从而可以看出噪声对弱测量放大的影响。
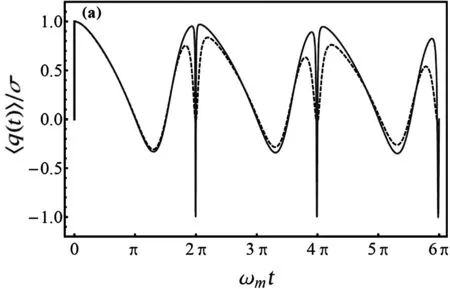
对于和θ=π/4,镜子的平均位移〈q(t)〉/σ是时间ωmt的函数,其中k=0.005,γ=0(实线)和γ=0.005(虚线)。
镜子的平均位移〈q(t)〉/σ在图3中显示为时间ωmt的函数,其中k=0.005,γ=0(实线)和γ=0.005(虚线)。从图3可以看出,在存在阻尼的情况下,所有的放大值都减小了(虚线),但是实际的γ可以很小(在文献[16]中γ=5×10-7)。例如,对于γ=5×10-7,这个放大结果与γ=0的结果几乎相同,因此耗散对镜子的放大效应几乎无影响。
5 结论
总之,本文在光机械系统中用相干态指针研究了弱测量放大。之所以被认为是一种新的放大机制,那是因为后选择后指针态之间的相对相位是由于量子力学的非对易性引起的,这与标准的弱测量(WVA regime)不同[1,6],后者是通过对被测量系统的后选择(对被测系统进行投影测量)获得相对相位。当镜子处于相干态时,镜子位置的位移的最大放大值可以在ωm(t)=0附近发生,然而如果镜子处于基态时,则无法实现放大效应[1,6,15]。该结果依赖于品质因子差的光机械腔,因此本文的方案在当前实验条件下是可行的。这些结果扩展了弱测量在光学机械系统中的应用,并且加深了我们对弱测量的理解。
